算法导论 — 思考题6-3 Young氏矩阵

（Young氏矩阵）在一个$m\times n$的Young氏矩阵(Young tableau)中，每一行的数据都是从左到右排序，每一列的数据都是从上到下排序的。Young氏矩阵中也会存在一些值为$\infty$的数据项，表示那些不存在的元素。因此，Young氏矩阵可以用来存储$r\le mn$个有限的数。
　　a. 画出一个包含元素为{9, 16, 3, 2, 4, 8, 5, 14, 12}的4×4 Young氏矩阵。
　　b. 对于一个$m\times n$的Young氏矩阵$Y$来说，请证明：如果$Y[1,1]=\infty$，则$Y$为空；如果$Y[m,n]<\infty$，则$Y$为满（即包含$mn$个元素）。
　　c. 请给出一个在$m\times n$ Young氏矩阵上时间复杂度为$O(m+n)$的EXTRACT-MIN的算法实现。你的算法可以考虑使用一个递归过程，它可以把一个规模为$m\times n$的问题分解为规模为$(m-1)\times n$或者$m\times (n-1)$的子问题（提示：考虑使用MAX-HEAPIFY）。这里，定义$T(p)$用来表示EXTRACT-MIN在任一$m\times n$的Young氏矩阵上的时间复杂度，其中$p=m+n$。给出并求解$T(p)$的递归表达式，其结果为$O(m+n)$。
　　d. 试说明如何在$O(m+n)$时间内，将一个新元素插入到一个未满的$m\times n$的Young氏矩阵中。
　　e. 在不用其他排序算法的情况下，试说明如何利用一个$n\times n$的Young氏矩阵在$O(n^3)$的时间内将$n^2$个数进行排序。
　　f. 设计一个时间复杂度为$O(m+n)$的算法，它可以用来判断一个给定的数是否存储在$m\times n$的Young氏矩阵中。
　　
　　解
　　a.
　　
　　
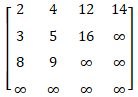
　　b.
　　先给出Young氏矩阵的性质1：对于矩阵中的任意一个元素$Y[i,j]$，如果$i^{\prime }\le i$并且$j^{\prime }\le j$，那么一定有$Y[i^{\prime },j^{\prime }]\le Y[i,j]$。下面我们来证明这个性质。
　　由于在同一行中，左边的元素不大于右边的元素，所以有$Y[i^{\prime },j^{\prime }]\le Y[i^{\prime },j]$ (因为$j^{\prime }\le j$，所以$Y[i^{\prime },j^{\prime }]$位于$Y[i^{\prime },j]$的左边，或者二者是同一个元素)。又由于在同一列中，上边的元素不大于下边的元素，所以有$Y[i^{\prime },j]\le Y[i,j]$（因为$i^{\prime }\le i$，所以$Y[i^{\prime },j]$在$Y[i,j]$的上边，或者二者是同一个元素）。综上所述，有$Y[i^{\prime },j^{\prime }]\le Y[i^{\prime },j]\le Y[i,j]$。所以上述性质是成立的。
　　类似地，可以得到另外一个性质2：对于矩阵中的任意一个元素$Y[i,j]$，如果$i^{\prime }\ge i$并且$j^{\prime }\ge j$，那么一定有$Y[i^{\prime },j^{\prime }]\ge Y[i,j]$。
　　现在我们来看题目要求我们证明的结论。如果$Y[1,1]=\infty$，那么根据性质2，$Y$中任意一个元素都满足$Y[i,j]\ge Y[1,1]=\infty$ (因为$i\ge 1$并且$j\ge 1$)，即$Y$中的所有元素都为$\infty$，所以$Y$为空。
　　如果$Y[m,n]<\infty$，那么根据性质1，$Y$中任意一个元素都满足$Y[i,j]\le Y[m,n]<\infty$ (因为$i\le m$并且$j\le n$)，即$Y$中的所有元素都不为$\infty$，所以Y为满。
　　
　　c.
　　根据上文性质2，Young氏矩阵中的任意一个元素必然满足$Y[i,j]\ge Y[1,1]$，所以$Y[1,1]$一定是最小的元素。EXTRACT-MIN先将$Y[1,1]$取出，然后将$Y[1,1]$赋值为$\infty$，这时$Y[1,1]$有可能破坏Young氏矩阵的性质，可以用类似MIN-HEAPIFY的方法来维护Young氏矩阵的性质。
　　
　　YOUNG-MATRIX-EXTRACT-MIN中每次while迭代，要么让$i$加$1$，要么让$j$加$1$，最坏情况一直让$i$加到$m$并且$j$加到$n$为止。因此while迭代次数最多为$m+n$。故YOUNG-MATRIX-EXTRACT-MIN的时间复杂度为$O(m+n)$。下图给出了一个YOUNG-MATRIX-EXTRACT-MIN的例子。
　　
　　
　　d.
　　根据b的结论，如果一个Young氏矩阵未满，那么$Y[m,n]$一定为$\infty$。将$Y[m,n]$赋值为要插入的元素值，这样$Y[m,n]$有可能违反Young氏矩阵的性质。然后采用类似最小堆的HEAP-DECREASE-KEY方法，来将$Y[m,n]$交换到正确的位置。
　　
　　YOUNG-MATRIX-INSERT的时间复杂度与YOUNG-MATRIX-EXTRACT-MIN一样，都为$O(m+n)$。下图给出了一个YOUNG-MATRIX-INSERT的例子。
　　
　　
　　e.
　　建立一个$n\times n$的Young氏矩阵，用INSERT将每一个元素依次插入矩阵中。每插入一个元素耗时$O(n+n)=O(n)$，一共有$n^2$个元素，因此插入所有元素耗时$O(n^3)$。再调用EXTRACT-MIN依次提取出最小元素即可完成排序，这一步所花费的时间也为$O(n^3)$。
　　
　　f.
　　假设要寻找的元素为$x$。从Young氏矩阵左下角元素$Y[m,1]$开始搜索，分$3$种情况：
　　1) $x>Y[m,1]$
　　说明$x$不可能出现在第$1$列 (因为$Y[m,1]$为第$1$列的最大元素)，只可能出现在第$1$列的右边，所以现在忽略第$1$列，以第$2$列的最后一个元素$Y[m,2]$作为新的左下角元素重新进行搜索。
　　2) $x<Y[m,1]$
　　说明$x$不可能出现在第$m$行 (因为$Y[m,1]$为第$m$行的最小元素)，只可能出现在第$m$行的上面，所以现在忽略第$m$行，以第$m-1$行的第一个元素$Y[m-1,1]$作为新的左下角元素重新搜索。
　　3) $x=Y[m,1]$
　　已经找到所需元素。
　　按以上流程迭代，直到找到所需元素为止，或者直到新的左下角元素已经超出了Young氏矩阵的范围为止，这种情况说明矩阵中没有我们要找的元素。
　　
　　很明显，YOUNG-MATRIX-SEARCH的时间复杂度也为$O(m+n)$。

本题的code链接。
　　https://github.com/yangtzhou2012/Introduction_to_Algorithms_3rd/tree/master/Chapter06/Problem_6-3