上篇通过线性方程组引入矩阵的概念，解决了当 A 是可逆矩阵时，可用高斯消元法求解线性方程组，并且给出解析解。本篇试图彻底解决 Ax = b 的解（A为一般矩阵时情形），并且引入了矩阵的四个基本子空间的概念。
为了论证一下，你的数学是不是体育老师教的，让我们先回忆一下，什么是矩阵的秩，什么是矩阵的零空间
介绍 Ax = b 之前，作为特例，先介绍 Ax = 0。
例：
很显然，依然可以采用高斯消元法，通过行变换，得到上三角矩阵 U。
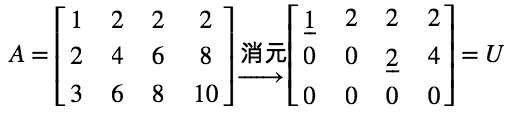
进一步进行行变换，可得到 R 矩阵(RREF, Reduced row echelon form, 简化行阶梯形式)。
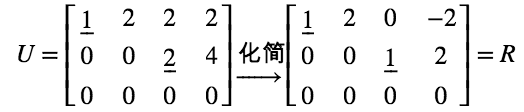
R 矩阵是行变换后的最简形式，主元均为1，且主元所在列其他元素均为0。
主列(pivot column)：主变量所在的列。
自由列(free column)：自由变量(非主变量)所在的列。
通常：将主元的个数，称为矩阵的秩（rank）。有多种定义 rank(A)，后面将逐步介绍，尽情期待。
显然 ，上面的 A。
rank(A) = rank(U) = rank(R) = 2；
#free(A) = #free(U) = #free(R) = n - r = 4 - 2 = 2。
性质：行变换不影响矩阵的 rank。
因为 A x = 0 等价于 R x = 0。
通常的做法，赋值自由变量，求解主变量，得到方程组的一组特解。
不妨设 x2 = 1, x4 = 0，回代到原方程组得到，
1·x1 + 2·1 + 0·x3 + (-2) ·0 = 0
0·x1 + 0·1 + 1·x3 + 4·0 = 0
不难求得：
x1 = -2, x3 = 0。
同理设 x2 = 0, x4 = 1，同理 x1 = 2, x3 = -2。
最终得到方程组的两组特解。
可以看出：特解的个数等于 = #free(A)，想象一下把自由变量取为单位矩阵I。
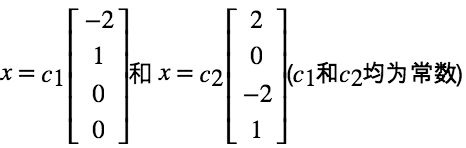
最终通解：
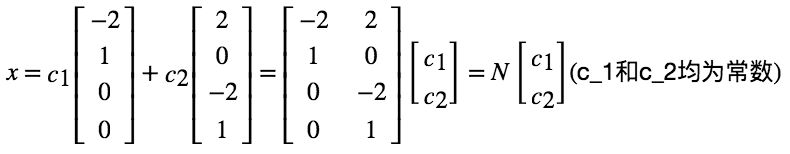
本篇后面会介绍向量空间，通解可以转化为矩阵 N 的列空间。
问题的关键变为求解 N（Nullspace Matrix, 零空间矩阵）。
通过列变换将 R 重组，其实就是将 x2/x3 所在列交换位置，最终再交换回来就可以了。
这样就把主变量、自由变量拆分开了，Ax = 0 最终变为：
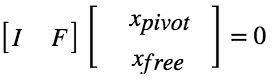
不难想到，令自由变量为单位阵(和上面的方式一致)，最终得到：
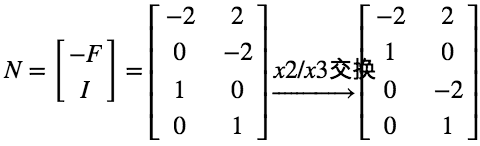
上篇介绍过方阵的 LR 分解。即 PA = LR。
利用 Gauss 消元法。
同样可以记录：A => R 的全过程，即为 E。
显然 E A = R => A = E^-1 R。
介绍完 Ax = 0, 终于可以介绍 Ax = b。将从“可解性”、“解法”、“四种基本情形” 三个方面分别介绍。
Ax = 0 一定有解（至少有一个零解，零空间），但是 Ax = b 不一定有解。
依然以 A 为例：
在其增广矩阵上做行变换。
那么，有解的必要条件：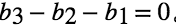 
充要条件：b 属于 A 的列空间 (本篇后面会介绍)。
求解 Ax = b 可以转化为两步：
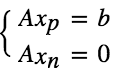
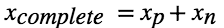
例：
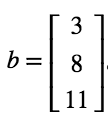
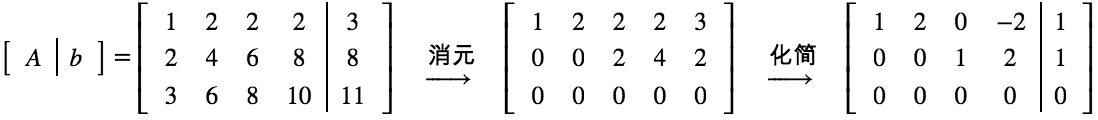
1. 寻找特解
令 x2 = 0, x4 = 0 => x1 = 1, x3 = 1。得到特解：
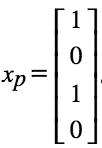
2. Ax = 0
前面已得到。
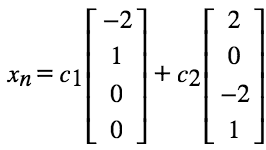
综合得到：
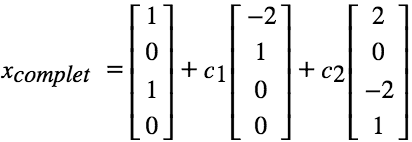
具体分为四种情况：
1. 列满秩( r = n )
2. 行满秩( r = m)
3. 行列满秩( r = m = n)
4. 行列均不满秩( r < m, r < n)
经过行变换：
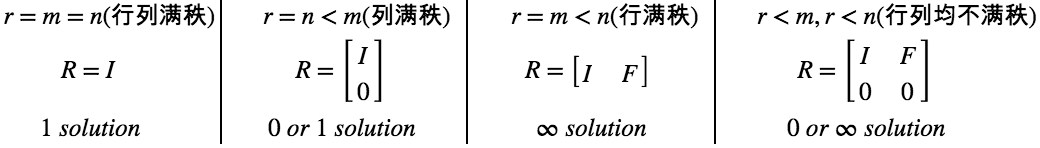
通常被称为线性空间，又被称为向量空间（自行百度）。
线性空间是定义在 加法 和 数乘 两种运算，并且满足 8 条基本性质（自行百度）。
要求：
1. 向量空间必须包含原点(Origin)。
2. 向量空间中任意向量的数乘、求和运算，得到的向量也在该空间之中。
对于向量空间 S 和 T， 那么 S ∩ T 也是向量空间，自行验证。
矩阵基本子空间之一：列空间 C(A)
A 的列向量所张成的空间，被称为 A 的列空间。
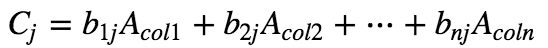
Ax = b 有非零解充要条件：b 属于 A 的列空间。
矩阵基本子空间之二：零空间 N(A)
Ax = 0 的解也构成空间，被称为矩阵 A 的零空间。
从上面例子中，可以看出 Ax = 0 的解的确是一个向量空间。
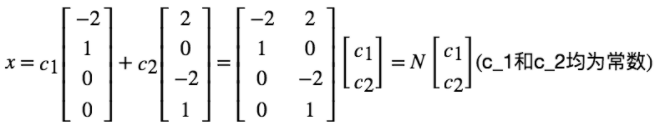
正好对应 N 的列空间。
矩阵基本子空间之三：行空间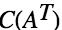 
矩阵 A 的行空间 = A^T 的列空间。
矩阵基本子空间之四：左零空间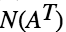 
左零空间空间的来由？
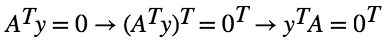
本文转载自我师弟的公众号，在此谢过！
1772
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
