[BZOJ 3111] ZJOI 2013 蚂蚁寻路 · 动态规划

BZOJ上没有题目，也是有点小坑……

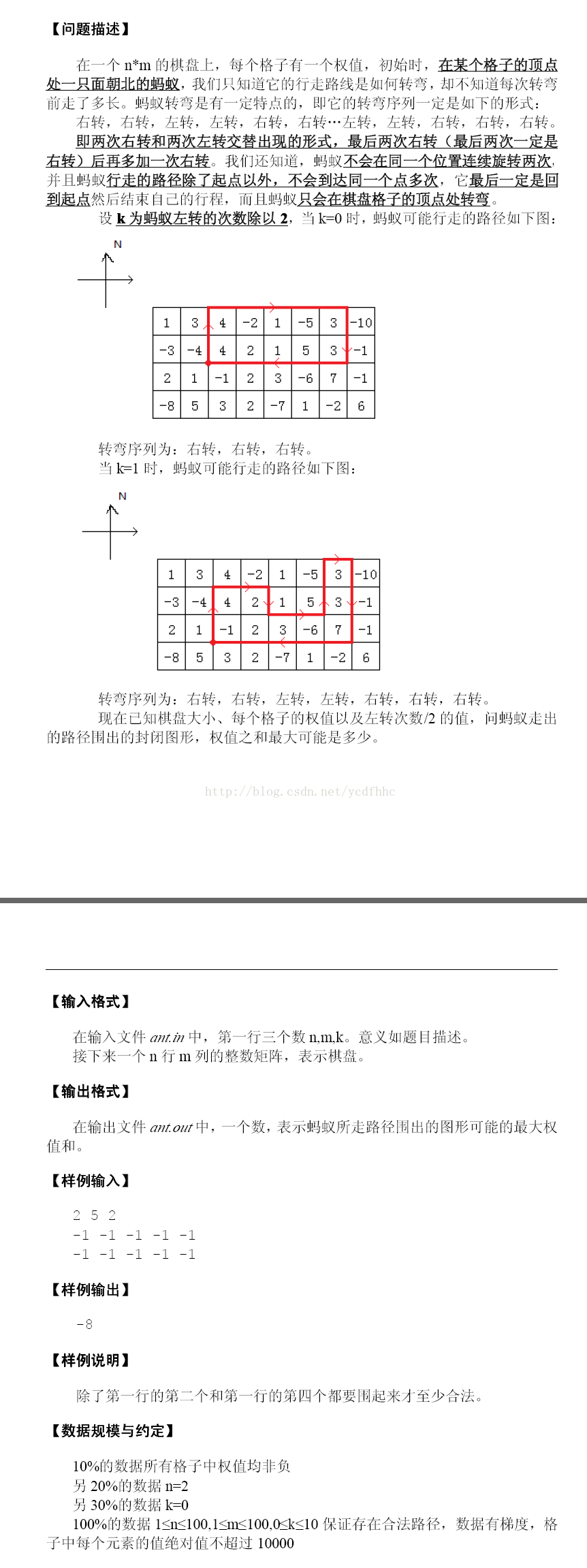
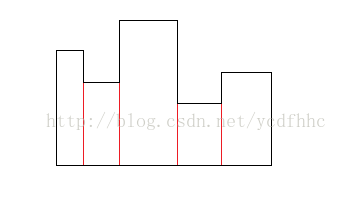
那么自己在草稿纸上画画写写就很容易发现，这题其实是要你在一个n*m大小的矩形中框出一个长城形状的子图，使得子图包含的权值和最大。框出图形的底和左右两边都是直的，上端是一高一低间隔排布，总共有2*k+1个（间隔k次）（如下图）

那么从图中我们可以看出，其实是要求2*k+1个同底的子矩形相连组合起来取得的最大和。

这种题目做的时候很容易往高维度想啊，f[i][j][p][h]表示当前这个子矩形的右下角为(i,j)，是第p个矩形，高度为h时取得的最优解。

g[i][j][p][h][0/1]表示当前这个子矩形的右下角为(i,j)，是第p个矩形，高度大于等于/小于等于h时的最优解。

得出转移方程：f[i][j][p][h]=max(f[i][j-1][p][h],g[i][j-1][p-1][h][p%2])+s[i][j]-s[h-1][j]

每得出一种转移方式，我们都要想，为什么是这样？

第一个f[i][j-1][p][h]就表示这一列与上一列还在同一个矩形内，变化的只是列+1。

第二个就表示从第j列开始是一个新的矩形。由于矩形是一高一低间隔排布，假设第p个矩形是高的，那么第p-1个矩形肯定要比它低，而高的矩形都是奇数号，所以就是g[i][j][j-1][p-1][h][p%2]，低的矩形也同理。

那么g[i][j][p][h][0/1]就在f[i][j][p][h]全更新完后，按照定义的性质从高到低和从低到高分别扫一遍，转移

     g[i][j][p][h][0]=max(g[i][j][p][h -1][0],f[i][j][p][h -1])

     g[i][j][p][h][1]=max(g[i][j][p][h+1][1],f[i][j][p][h+1])

边界条件为f[i][0][p][h]=g[i][0][p][h][1]=g[i][0][p][h][0]=-inf

最后ans用f[i][j][k][i],g[i][j][k][i][0]来更新（别问我为什么）

#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <iostream>
using namespace std;
#define inf 1000000000

const int maxn=120;
int n,m,k,ans,a[maxn][maxn],f[maxn][25][maxn],g[maxn][25][maxn][2],s[maxn][maxn];

int main(){
    scanf("%d%d%d",&n,&m,&k);
    k=k*2+1;
    for (int i=1;i<=n;i++)
        for (int j=1;j<=m;j++)
            scanf("%d",&a[i][j]),s[i][j]=s[i-1][j]+a[i][j];
	for (int i=1;i<=k;i++)
		for (int j=1;j<=n;j++)
			f[0][i][j]=g[0][i][j][0]=g[0][i][j][1]=-inf;
	ans=-inf;
	for (int i=1;i<=n;i++)
		for (int j=1;j<=m;j++){
			for (int p=1;p<=k;p++){
				for (int h=i;h;h--)
					f[j][p][h]=max(f[j-1][p][h],g[j-1][p-1][h][p%2])+s[i][j]-s[h-1][j];
				g[j][p][1][0]=-inf;
				for (int h=2;h<=i;h++)			
					g[j][p][h][0]=max(g[j][p][h-1][0],f[j][p][h-1]);
				g[j][p][i][1]=-inf;
	   			for (int h=i-1;h;h--)
	   				g[j][p][h][1]=max(g[j][p][h+1][1],f[j][p][h+1]);
			}
			ans=max(ans,max(f[j][k][i],g[j][k][i][0]));
		}
    printf("%d\n",ans);
	return 0;
}