人群与社会——第四周

4.1  博弈论的几个要素

博弈的条件：情景-》博弈-》求解

博弈：必须大于等于2个人进行博弈

每个人都是理性的，每个人会选择个人利益最大化，并且他知道别人也是追求利益最大化的。

博弈的决策条件：不商量，每个人让自己利益最大化。

4.2 考试-报告博弈和囚徒博弈

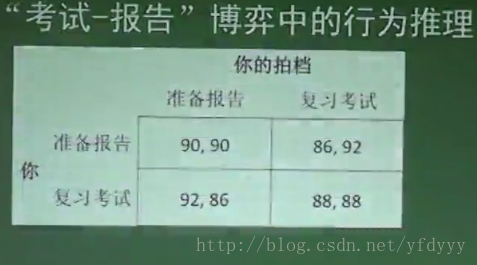
考试-报告博弈里面，两个人都有严格占优策略，所以他们都会选择严格占优策略。

对于你来说，如果对方准备报告，你复习比准备占优（92》90），如果对方复习，你复习比准备占优（88》86）;

对于你的对手来说，如果你复习，对手复习比报告占优（88》86）， 如果你准备报告，对手复习比准备报告占优（92》90）;

所以，当出现严格占优策略时，一定选择严格占优策略。

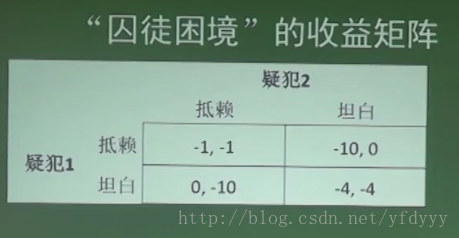
囚徒博弈里面，两个人也都有严格占优策略，所以当两个人都出现严格占优策略时，都会选择严格占优策略。

对于囚徒困境：疑犯1的严格占优策略是坦白，疑犯2的严格占优策略也是坦白，虽然严格占优策略并不是最有的策略，但是因为大家是独立思考的，不能够相关的讨论。

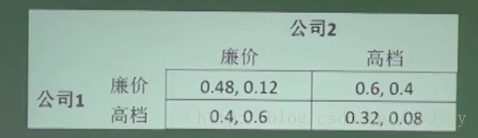
公司营销博弈：只有一个公司有严格占优策略，所以这个公司选择严格占优策略，另外一个公司会选择最佳应对策略。

对于公司1,有严格占优策略是廉价，所以公司1一定会选择廉价，而公司2应该选择最优应对，公司2选择廉价是0.12, 选择高档是0.4, 0.4优于0.12, 所以公司2的最佳应对是高档。当一个公司有严格占优策略时，该公司选择严格占优策略，而另外一个公司选择最佳应对。最佳应对一定存在，但可能有多个，因为最佳应对是》的关系，严格最近应对如果存在，则一定唯一。

如果两个人都没有严格占优策略的话，用纳什均衡（两个策略互为最佳应对策略）。

此时，公司1和公司2都没有严格占优策略，针对公司2的策略，公司1对选择AA，BB，CC来分别应对，而针对公司1的策略，公司2会选择AA，BC，CB来分别应对，所以AA策略是互为最佳应对策略的，所以公司1选择A策略，公司2选择A策略。

互为最佳应对的策略组是纳什均衡;

找最佳应对的策略：

分别找到应对策略，如果两个应对都落在同一个格子里面，则这个策略组就是互为最佳应对。

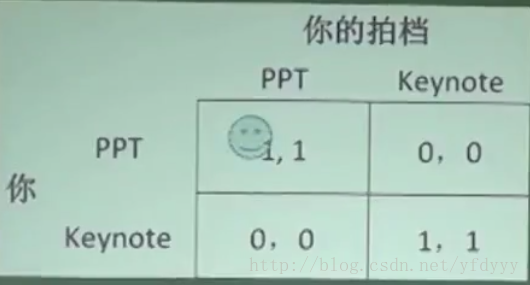
存在多个纳什均衡（协调博弈）

此时存在两个纳什均衡，ppt-ppt，keynote-keynote;仅从博弈的结构上面，不能够进行推导了，此时要引入一些外部的因素来帮助决策;

如果此时存在纳什均衡（），用纳什均衡；

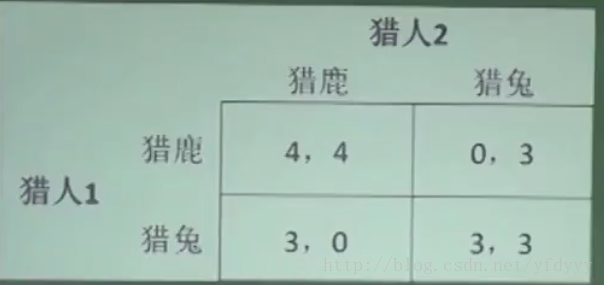
如果存在多个纳什均衡，考虑外部因素（猎鹿博弈）；

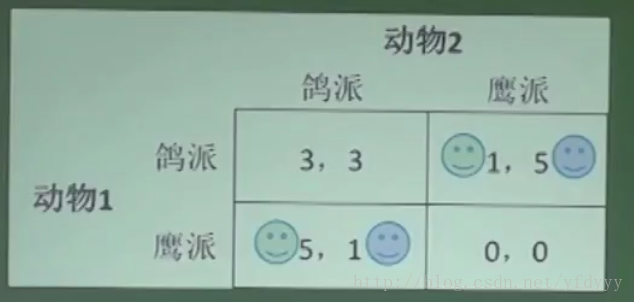
纳什均衡只能缩小预测范围，但是并不一定给出唯一的预测（鹰鸽博弈）；

几种多重博弈均衡的比较：

1.使用ppt或者keynote，2；有偏好的使用ppt和keynote；3.猎鹿博弈；4.鹰鸽博弈；

猎鹿博弈，的博弈均衡发生在猎鹿-猎鹿，猎兔-猎兔，均衡发生在两个人选择一样的;

但是鹰鸽博弈，均衡发生在两个人选择不一样;

博弈有助于缩小范围，但是不能够决定

4.3~4.4 混合博弈：

混合博弈，是重复做多组博弈，会出现一个概率p你做一个选择，1-p的概率做另外一个选择；对方会以q的概率做一个选择，1-q的概率做另外一个选择；

无差异原理，可以得到混合博弈的最佳应对（它们分别使得对方在两个纯策略选择上得到的回报无差异）。

社会最优，两个人获得的总收益最大化。社会最优和纳什均衡有可能一致（理想系统）。