二叉查找树(BST)和平衡二叉查找树(AVL)

二叉查找树（BST）

前一篇介绍了树，却未介绍树有什么用。但就算我不说，你也能想得到，看我们Windows的目录结构，其实就是树形的，一个典型的分类应用。当然除了分类，树还有别的作用，我们可以利用树建立一个非常便于查找取值又非常便于插入删除的数据结构，这就是马上要提到的二叉查找树（Binary Search Tree），这种二叉树有个特点：对任意节点而言，左子（当然了，存在的话）的值总是小于本身，而右子（存在的话）的值总是大于本身。

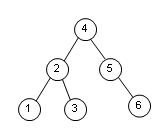
这种特性使得我们要查找其中的某个值都很容易，从根开始，小的往左找，大的往右找，不大不小的就是这个节点了；插入一样的道理，从根开始，小的往左，大的往右，直到叶子，就插入，算法比较简单，不一一列了，它们的时间复杂度期望为Ο(logn)。（为什么是“期望”，后面会讲）

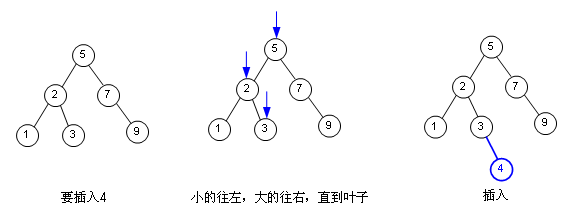
删除则稍微麻烦点，因为我们删的不一定是叶子，如果只是叶子，那就好办，如果不是呢？我们最通常的做法就是把这个节点往下挪，直到它变为叶子为止，看图。

也许你要问，如果和左子树最大节点交换后，要删除的节点依然不是叶子，那怎么办呢？那继续呗，看图：

那左子树不存在的情况下呢？你可以查找右子树的最小节点，和上面是类似的，图我就不画了。

平衡二叉查找树（AVL）

前面说了，二叉查找树方便查找取值插入删除，其复杂度不过为Ο(logn)，但这是个“期望值”，因为我们也有比较差的情况，比如下面这棵树：

说是树，其实已经退化为链表了，但从概念上来说它依然是一棵二叉查找树，这棵树怎么形成的呢？很简单，我们只要按着1，2，3，4，5，6，7这样的顺序往一个空的二叉查找树里添加元素，就形成了。这样我们再添加8，9，10……那真的就变成了一个链表结构，那插入的复杂度也就变成了Ο(n)。导致这种糟糕的原因是这棵树非常不平衡，右树的重量远大于左树，所以我们提出了一种叫“平衡二叉查找树”的结构，平衡二叉查找树英文叫AVL，而不是我本来以为的什么Balance BST，AVL来自于人名，我这里就不追究了。

平衡，顾名思义，就是两边看起来比较对称，但很多时候我们是做不到绝对的对称（绝对对称即对任意子树而言，左右节点的数量都相等），因为只有(2^n-1)元素数目的二叉树才能做到绝对对称，所以我们使用了“高度”（height）这么个概念，某节点的高度指的是它离它的子树的叶子的最远距离：

那么我再引申出两个概念，左高和右高：
左高 = 左节点空 ? 0 : (左节点高+1)
右高 = 右节点空 ? 0 : (右节点高+1)

那我们就可以给AVL下个定义了，对AVL的任意节点而言：

ABS(左高 - 右高) <= 1

做到了这点，这棵树看起来就比较平衡了，如何生成一棵AVL树呢？算法十分不简单，那我们先通过图来获得一些最直观的认识，就先按1，2，3，4……这样的自然数顺序加入到树中，下图体现出了树的构造变化：

随着新节点的加入，树自动调整自身结构，达到新的平衡状态，这就是我们想要的AVL树。我们先要分析，为什么树会失衡？是由于插入了一个元素，对吧，那我们能不能把不同的插入情况全部概括起来并作出统一的调整来使得树重新平衡？答案是肯定的，也有人帮我们研究好了，只是证明这个过程需要一些数学功底，我是不行的了，所以直接给出算法示意图和范例。

LL型调整：

再给一个LL型调整的实例：

RR型调整，其实就是LL型调整的镜像而已：

这是一个RR型调整的实例：

接下去就是LR型调整：

这是一个LR型调整的实例：

RL型调整是LR型调整的镜像，所以不再画图了。

至于如何选择不同的调整类型，我后面将给出代码，看“DoBalance”这个函数的实现，很清晰的。那接下去我们还要面临一个比较困难的问题，就是删除及删除平衡，因为不光是插入元素可能导致不平衡，删除也会。不过我们都有个同样的前提，就是无论是插入前还是删除前的二叉树，都是平衡的。

我参考的书上说删除和插入其实是很类似的，具体实现却没说，我后来写代码蛮辛苦的，最后发现确实差别不大，但在调整相关节点高度的时候确实有点细微上的差别，这个在我的代码里也能看得出来。下面我就给出我的代码，我已经通过了初步的测试，不过也许代码还有bug，如果发现了，请留言。

代码比较长，其中还利用了之前的堆栈和队列结构，可以算是复习，如果觉得代码晦涩难懂，也可以跳过，有些怕自己的代码写得不够好……

另附带一些代码说明：
1，TreeNode目前只带一个“数据”，就是iData，所以交换节点位置时候，为了方便，只需要交换这个数据；
2，代码中的pMinBST指向的是“最小不平衡树”，即：从插入或删除的位置开始往上查找出现的第一个不平衡的节点；
3，“往上查找”就需要借助一个Stack结构；
4，AVL树的析构采用了后序遍历，由于是析构，之后不再用到，所以后序遍历时候改变了节点指针的值，后续遍历使用了Queue结构；
5，删除节点时候，寻找并交换叶子节点的操作有些晦涩，往左寻找最大节点，为什么找到了最大并交换，而它还不是叶子的时候，我只需要再往左找并交换一次就可以了呢？因为我删除到时候有个前提：这棵树是平衡的，往右寻找最小节点的道理跟这个一样的；
6，有什么问题请留言。

#include  " stdio.h "

//  TreeNode
//
struct  TreeNode
{
    TreeNode( int  iVal);
     int  UpdateHeight();
     int  GetLeftHeight();
     int  GetRightHeight();
     int  GetDiff();  // Left Height - Right height

     int  iData;

     int  iHeight;
    TreeNode *  pLeft;
    TreeNode *  pRight;
};

TreeNode::TreeNode( int  iVal)
{
    iData  =  iVal;
    iHeight  =   0 ;
    pLeft  =   0 ;
    pRight  =   0 ;
}

int  TreeNode::UpdateHeight()
{
     int  iHeightLeft  =  GetLeftHeight();
     int  iHeightRight  =  GetRightHeight();
     if (iHeightLeft == 0   &&  iHeightRight == 0 )
        iHeight  =   0 ;
     else
        iHeight  =  (iHeightLeft > iHeightRight) ? (iHeightLeft):(iHeightRight);
     return  iHeight;
}

int  TreeNode::GetLeftHeight()
{
     if (pLeft != 0 )
         return  pLeft -> iHeight  +   1 ;
     else
         return   0 ;
}

int  TreeNode::GetRightHeight()
{
     if (pRight != 0 )
         return  pRight -> iHeight  +   1 ;
     else
         return   0 ;
}

int  TreeNode::GetDiff()
{
     int  iHeightLeft  =   0 ;
     int  iHeightRight  =   0 ;
    
     if (pLeft != 0 )
        iHeightLeft  =  pLeft -> iHeight  +   1 ;
     if (pRight != 0 )
        iHeightRight  =  pRight -> iHeight  +   1 ;

     return  iHeightLeft  -  iHeightRight;
}

//  Stack
//
class  Stack
{
public :
    Stack( int  iAmount  =   10 );
     ~ Stack();
    
     // return 1 means succeeded, 0 means failed.
     int  Pop(TreeNode *   &  val);
     int  Push(TreeNode *  val);
     int  Top(TreeNode *   &  val);

     // iterator
     int  GetTop(TreeNode *   & val);
     int  GetNext(TreeNode *   & val);
private :
    TreeNode **  m_pData;
     int  m_iCount;
     int  m_iAmount;

     // iterator
     int  m_iCurr;
};

Stack::Stack( int  iAmount)
{
    m_pData  =   new  TreeNode * [iAmount];
    m_iCount  =   0 ;
    m_iAmount  =  iAmount;
    m_iCurr  =   0 ;
}

Stack:: ~ Stack()
{
    delete m_pData;
}

int  Stack::Pop(TreeNode *   &  val)
{
     if (m_iCount > 0 )
    {
         -- m_iCount;
        val  =  m_pData[m_iCount];
         return   1 ;
    }
     return   0 ;
}

int  Stack::Push(TreeNode *  val)
{
     if (m_iCount < m_iAmount)
    {
        m_pData[m_iCount]  =  val;
         ++ m_iCount;
         return   1 ;
    }
     return   0 ;
}

int  Stack::Top(TreeNode *   &  val)
{
     if (m_iCount > 0   &&  m_iCount <= m_iAmount)
    {
        val  =  m_pData[m_iCount - 1 ];
         return   1 ;
    }
     return   0 ;
}

int  Stack::GetTop(TreeNode *   & val)
{
     if (m_iCount > 0   &&  m_iCount <= m_iAmount)
    {
        val  =  m_pData[m_iCount - 1 ];
        m_iCurr  =  m_iCount  -   1 ;
         return   1 ;
    }
     return   0 ;
}

int  Stack::GetNext(TreeNode *   & val)
{
     if ((m_iCurr - 1 ) < (m_iCount - 1 )  &&  (m_iCurr - 1 ) >= 0 )
    {
         -- m_iCurr;
        val  =  m_pData[m_iCurr];
         return   1 ;
    }
     return   0 ;
}

//  The Queue
//
class  Queue
{
public :
    Queue( int  iAmount = 10 );
     ~ Queue();
    
     // return 0 means failed, return 1 means succeeded.
     int  Enqueue(TreeNode *  node);
     int  Dequeue(TreeNode *   &  node);
private :
     int  m_iAmount;
     int  m_iCount;
    TreeNode **  m_ppFixed;  // The pointer array to implement the queue.
    
     int  m_iHead;
     int  m_iTail;
};

Queue::Queue( int  iAmount)
{
    m_iCount  =   0 ;
    m_iAmount  =  iAmount;
    m_ppFixed  =   new  TreeNode * [iAmount];
    
    m_iHead  =   0 ;
    m_iTail  =  iAmount - 1 ;
}

Queue:: ~ Queue()
{
    delete[] m_ppFixed;
}

int  Queue::Enqueue(TreeNode *  node)
{
     if (m_iCount < m_iAmount)
    {
         ++ m_iTail;
         if (m_iTail  >  m_iAmount - 1 )
            m_iTail  =   0 ;
        m_ppFixed[m_iTail]  =  node;
         ++ m_iCount;
         return   1 ;
    }
     else
         return   0 ;
}

int  Queue::Dequeue(TreeNode *   &  node)
{
     if (m_iCount > 0 )
    {
        node  =  m_ppFixed[m_iHead];
         ++ m_iHead;
         if (m_iHead  >  m_iAmount - 1 )
            m_iHead  =   0 ;
         -- m_iCount;
         return   1 ;
    }
     else
         return   0 ;
}

//  AVLTree
//
class  CAVLTree
{
public :
    CAVLTree();
     ~ CAVLTree();
    
    TreeNode *  Insert( int  iVal);
     int  Delete( int  iVal);
    TreeNode *  FindNode( int  iVal);  // the find function, returns 0 means not found.
    
#ifdef _DEBUG
     void  PrintTree();
#endif

protected :
     // Update the height after insert or delete.
     // And find the minimum unbalance BST.
     int  UpdateHeight(Stack  & st, TreeNode *   & pMinBST, TreeNode *   & pMinBSTParent,  int &  iLeftRight);

     // Rotate
     void  DoBalance(TreeNode  * pNode, TreeNode *  pMinBSTParent,  int  iLeftRight);
     void  LLRotate(TreeNode  * pNode, TreeNode *  pMinBSTParent,  int  iLeftRight);
     void  RRRotate(TreeNode  * pNode, TreeNode *  pMinBSTParent,  int  iLeftRight);
     void  LRRotate(TreeNode  * pNode, TreeNode *  pMinBSTParent,  int  iLeftRight,  int  iSpecialFlag = 0 );
     void  RLRotate(TreeNode  * pNode, TreeNode *  pMinBSTParent,  int  iLeftRight,  int  iSpecialFlag = 0 );
    
     void  SwapTwoNodes(TreeNode  * pNode1, TreeNode  * pNode2);  // Swap their value only.

    TreeNode  * m_pRoot;
};

CAVLTree::CAVLTree()
{
    m_pRoot  =  NULL;
}

CAVLTree:: ~ CAVLTree()
{
    Stack st( 40 );  // 2^40 must be enough.

     // Postorder traverse the tree to release all nodes.
    TreeNode  * pNode  =  m_pRoot;
    TreeNode  * pTemp;
     if (pNode == 0 )
         return ;

     while  ( 1 )
    {
         if (pNode -> pLeft != 0 )
        {
            st.Push(pNode);
            pTemp  =  pNode;
            pNode  =  pNode -> pLeft;
            pTemp -> pLeft  =   0 ;
             continue ;
        }
        
         if (pNode -> pRight != 0 )
        {
            st.Push(pNode);
            pTemp  =  pNode;
            pNode  =  pNode -> pRight;
            pTemp -> pRight  =   0 ;
             continue ;
        }
        
        delete pNode;

         if ( 0 == st.Pop(pNode))
             break ;
    }
}

TreeNode *  CAVLTree::Insert( int  iVal)
{
    Stack st( 40 );  // To record the path.
    TreeNode  * pNode  =  m_pRoot;
    TreeNode  * pIns;
     int  iLeftOrRight;  //  0 means left, 1 means right.
     while  ( 1 )
    {
         if (pNode == 0 )  // Insert at this position
        {
            TreeNode  * pNew  =   new  TreeNode(iVal);
            TreeNode  * pPrev;
             if ( 0 != st.Top(pPrev))
            {
                 if ( 0 == iLeftOrRight)
                    pPrev -> pLeft  =  pNew;
                 else
                    pPrev -> pRight  =  pNew;
            }
             else   // The root
            {
                m_pRoot  =  pNew;
                 return  m_pRoot;
            }

            pIns  =  pNew;
             if ( 0 == iLeftOrRight  &&  pPrev -> pRight != 0   ||   1 == iLeftOrRight  &&  pPrev -> pLeft != 0 )  // Need not to change.
                 return  pIns;

             break ;
        }

         if (iVal < pNode -> iData)
        {
            st.Push(pNode);
            pNode  =  pNode -> pLeft;
            iLeftOrRight  =   0 ;
        }
         else   if (iVal > pNode -> iData)
        {
            st.Push(pNode);
            pNode  =  pNode -> pRight;
            iLeftOrRight  =   1 ;
        }
         else
             return  pNode;
    }

    TreeNode *  pMinBST;
    TreeNode *  pMinBSTParent;
     int  iLRParent;
    UpdateHeight(st, pMinBST, pMinBSTParent, iLRParent);
     if (pMinBST != 0 )  // It exists. need balance.
    {
        DoBalance(pMinBST, pMinBSTParent, iLRParent);
    }
     return  pIns;
}

// Update the height after insert or delete.
int  CAVLTree::UpdateHeight(Stack  & st, TreeNode *   & pMinBST, TreeNode *   & pMinBSTParent,  int &  iLRParent)
{
    TreeNode  * pNode;
    pMinBST  =   0 ;
    pMinBSTParent  =   0 ;

     if ( 0 == st.GetTop(pNode))
         return   0 ;
    
     while ( 1 )
    {
        pNode -> UpdateHeight();
         int  iDiff  =  pNode -> GetDiff();
         if (iDiff > 1   ||  iDiff <- 1 )  // unbalance
        {
            pMinBST  =  pNode;
             if ( 0 != st.GetNext(pMinBSTParent))
            {
                 if (pMinBSTParent -> pLeft == pMinBST)
                    iLRParent  =   0 ;  // left
                 else
                    iLRParent  =   1 ;  // right
            }
             return   0 ;
        }

         if ( 0 == st.GetNext(pNode))
             break ;
    }

     return   0 ;
}

void  CAVLTree::DoBalance(TreeNode  * pNode, TreeNode *  pMinBSTParent,  int  iLeftRight)
{
     if (pNode -> GetLeftHeight()  <  pNode -> GetRightHeight())
    {
         if (pNode -> pRight -> GetLeftHeight()  <  pNode -> pRight -> GetRightHeight())
            RRRotate(pNode, pMinBSTParent, iLeftRight);
         else   if (pNode -> pRight -> GetLeftHeight()  >  pNode -> pRight -> GetRightHeight())
            RLRotate(pNode, pMinBSTParent, iLeftRight);
         else
            RLRotate(pNode, pMinBSTParent, iLeftRight,  1 );
    }
     else
    {
         if (pNode -> pLeft -> GetLeftHeight()  >  pNode -> pLeft -> GetRightHeight())
            LLRotate(pNode, pMinBSTParent, iLeftRight);
         else   if (pNode -> pLeft -> GetLeftHeight()  <  pNode -> pLeft -> GetRightHeight())
            LRRotate(pNode, pMinBSTParent, iLeftRight);
         else
            LRRotate(pNode, pMinBSTParent, iLeftRight,  1 );
    }
}

//       B               A
//      / \             / \
//     A   BR    =>    AL  B
//    / \              +  / \
//   AL  AR              AR  BR
//   +
void  CAVLTree::LLRotate(TreeNode  * pNode, TreeNode *  pMinBSTParent,  int  iLeftRight)
{
     // B, A and AL must be exist. BR and AR may be null.
    TreeNode  * pNodeB  =  pNode;
    TreeNode  * pNodeA  =  pNodeB -> pLeft;
    TreeNode  * pNodeAR  =  pNodeA -> pRight;
    pNodeA -> pRight  =  pNodeB;
    pNodeB -> pLeft  =  pNodeAR;

     // Handle the height
    pNodeB -> iHeight  -=   2 ;

     if (pMinBSTParent == 0 )  // root
        m_pRoot  =  pNodeA;
     else
    {
         if (iLeftRight == 0 )  // left
            pMinBSTParent -> pLeft  =  pNodeA;
         else
            pMinBSTParent -> pRight  =  pNodeA;
    }
}

//       A                B
//      / \              / \
//     AL  B      =>    A   BR
//        / \          / \  +
//       BL  BR       AL  BL
//           +
void  CAVLTree::RRRotate(TreeNode  * pNode, TreeNode *  pMinBSTParent,  int  iLeftRight)
{
    TreeNode  * pNodeA  =  pNode;
    TreeNode  * pNodeB  =  pNodeA -> pRight;
    TreeNode  * pNodeBL  =  pNodeB -> pLeft;
    pNodeB -> pLeft  =  pNodeA;
    pNodeA -> pRight  =  pNodeBL;

     // Handle the height
    pNodeA -> iHeight  -=   2 ;

     if (pMinBSTParent == 0 )  // root
        m_pRoot  =  pNodeB;
     else
    {
         if (iLeftRight == 0 )  // left
            pMinBSTParent -> pLeft  =  pNodeB;
         else
            pMinBSTParent -> pRight  =  pNodeB;
    }
}

//           C                   B
//          / \                /   \
//         A   CR             A     C
//        / \         =>     / \   / \
//       AL  B              AL BL BR CR
//          / \                   +
//         BL  BR
//             +
//  Special flag is used for some kind of delete operation, for example:
//         4                   3
//        / \                 / \
//       2   5(-)    =>      2   4
//      / \                 /
//     1   3               1
void  CAVLTree::LRRotate(TreeNode  * pNode, TreeNode *  pMinBSTParent,  int  iLeftRight,  int  iSpecialFlag)
{
    TreeNode  * pNodeC  =  pNode;
    TreeNode  * pNodeA  =  pNodeC -> pLeft;
    TreeNode  * pNodeB  =  pNodeA -> pRight;
    TreeNode  * pNodeBL  =  pNodeB -> pLeft;
    TreeNode  * pNodeBR  =  pNodeB -> pRight;
    pNodeB -> pLeft  =  pNodeA;
    pNodeB -> pRight  =  pNodeC;
    pNodeA -> pRight  =  pNodeBL;
    pNodeC -> pLeft  =  pNodeBR;

     // Handle the height
     if (iSpecialFlag == 0 )
    {
        pNodeA -> iHeight  -=   1 ;
        pNodeB -> iHeight  +=   1 ;
    }
     else
    {
        pNodeB -> iHeight  +=   2 ;
    }
    pNodeC -> iHeight  -=   2 ;

     if (pMinBSTParent == 0 )  // root
        m_pRoot  =  pNodeB;
     else
    {
         if (iLeftRight == 0 )  // left
            pMinBSTParent -> pLeft  =  pNodeB;
         else
            pMinBSTParent -> pRight  =  pNodeB;
    }
}

//           B                   A
//          / \                /   \
//         BL  C              B     C
//            / \      =>    / \   / \
//           A   CR         BL AL AR CR
//          / \                   +
//         AL  AR
//             +
//  Special flag is used for some kind of delete operation, for example:
//         3                   4
//        / \                 / \
//    (-)2   5      =>       3   5
//          / \                   \
//         4   6                   6
void  CAVLTree::RLRotate(TreeNode  * pNode, TreeNode *  pMinBSTParent,  int  iLeftRight,  int  iSpecialFlag)
{
    TreeNode  * pNodeB  =  pNode;
    TreeNode  * pNodeC  =  pNodeB -> pRight;
    TreeNode  * pNodeA  =  pNodeC -> pLeft;
    TreeNode  * pNodeAL  =  pNodeA -> pLeft;
    TreeNode  * pNodeAR  =  pNodeA -> pRight;
    pNodeA -> pLeft  =  pNodeB;
    pNodeA -> pRight  =  pNodeC;
    pNodeC -> pLeft  =  pNodeAR;
    pNodeB -> pRight  =  pNodeAL;

     // Handle the height
     if (iSpecialFlag == 0 )
    {
        pNodeC -> iHeight  -=   1 ;
        pNodeA -> iHeight  +=   1 ;
    }
     else
    {
        pNodeA -> iHeight  +=   2 ;
    }
    pNodeB -> iHeight  -=   2 ;
    
     if (pMinBSTParent == 0 )  // root
        m_pRoot  =  pNodeA;
     else
    {
         if (iLeftRight == 0 )  // left
            pMinBSTParent -> pLeft  =  pNodeA;
         else
            pMinBSTParent -> pRight  =  pNodeA;
    }
}

int  CAVLTree::Delete( int  iVal)
{
     if (m_pRoot == 0 )
         return   0 ;

    Stack st( 40 );  // To record the path.
    TreeNode  * pNode  =  m_pRoot;
    TreeNode  * pPrev;
     int  iLeftOrRight;  //  0 means left, 1 means right.

     while  ( 1 )
    {
         if (pNode -> iData == iVal)  // Yes, it is.
        {
            st.Push(pNode);
             break ;
        }

         if (iVal < pNode -> iData)
        {
            st.Push(pNode);
             if (pNode -> pLeft != 0 )
                pNode  =  pNode -> pLeft;
             else
                 return   0 ;
            iLeftOrRight  =   0 ;
        }
         else   // iVal > pNode->iData
        {
            st.Push(pNode);
             if (pNode -> pRight != 0 )
                pNode  =  pNode -> pRight;
             else
                 return   0 ;
            iLeftOrRight  =   1 ;
        }
    }
    
     int  iLeafLeftRight;

     if (pNode -> iHeight == 0 )  // It is the leaf node.
    {
         if ( 0 != st.GetTop(pPrev))
        {
            iLeafLeftRight  =  iLeftOrRight;
        }
         else   // The root, this tree is going to be null.
        {
            delete m_pRoot;
            m_pRoot  =   0 ;
             return   0 ;
        }
    }
     else   if (pNode -> pLeft != NULL)
    {
        iLeafLeftRight  =   0 ;
         // Move this node to the bottom.
        TreeNode  * pBiggestLeft  =  pNode -> pLeft;
        st.Push(pBiggestLeft);
         while (pBiggestLeft -> pRight != NULL)
        {
            pBiggestLeft  =  pBiggestLeft -> pRight;
            st.Push(pBiggestLeft);
            iLeafLeftRight  =   1 ;
        }
        SwapTwoNodes(pBiggestLeft, pNode);
         if (pBiggestLeft -> pLeft != NULL)
        {
            SwapTwoNodes(pBiggestLeft, pBiggestLeft -> pLeft);
            st.Push(pBiggestLeft -> pLeft);
            iLeafLeftRight  =   0 ;
        }
    }
     else   // pNode->pRight!=NULL
    {
        iLeafLeftRight  =   1 ;
         // Move this node to the bottom.
        TreeNode  * pLeastRight  =  pNode -> pRight;
        st.Push(pLeastRight);
         while (pLeastRight -> pLeft != NULL)
        {
            pLeastRight  =  pLeastRight -> pLeft;
            st.Push(pLeastRight);
            iLeafLeftRight  =   0 ;
        }
        SwapTwoNodes(pLeastRight, pNode);
         if (pLeastRight -> pRight != NULL)
        {
            SwapTwoNodes(pLeastRight, pLeastRight -> pRight);
            st.Push(pLeastRight -> pRight);
            iLeafLeftRight  =   1 ;
        }
    }

     // Delete the leaf.
    TreeNode  * pToDel;
    st.Pop(pToDel);
    delete pToDel;
    TreeNode  * pToChange;
    st.GetTop(pToChange);
     if (iLeafLeftRight == 0 )
        pToChange -> pLeft  =   0 ;
     else
        pToChange -> pRight  =   0 ;

    TreeNode *  pMinBST;
    TreeNode *  pMinBSTParent;
     int  iLRParent;
    UpdateHeight(st, pMinBST, pMinBSTParent, iLRParent);
     if (pMinBST != 0 )  // It exists. need balance.
    {
        DoBalance(pMinBST, pMinBSTParent, iLRParent);
    }

     return   0 ;
}

TreeNode *  CAVLTree::FindNode( int  iVal)
{
    TreeNode *  pNode  =  m_pRoot;
     while  (pNode != 0 )
    {
         if (iVal < pNode -> iData)
            pNode  =  pNode -> pLeft;
         else   if (iVal > pNode -> iData)
            pNode  =  pNode -> pRight;
         else
             return  pNode;
    }

     return   0 ;
}

void  CAVLTree::SwapTwoNodes(TreeNode  * pNode1, TreeNode  * pNode2)
{
     int  iDataTmp  =  pNode1 -> iData;

    pNode1 -> iData  =  pNode2 -> iData;

    pNode2 -> iData  =  iDataTmp;
}

#ifdef _DEBUG

void  CAVLTree::PrintTree()
{
    printf( " --------------------\n " );
     if (m_pRoot == 0 )
    {
        printf( " null tree.\n " );
         return ;
    }
    Queue que( 100 );
    que.Enqueue(m_pRoot);
    TreeNode *  pNode;
     while  ( 0 != que.Dequeue(pNode))
    {
         if (pNode -> pLeft != 0   &&  pNode -> pRight != 0 )
        {
            printf( " %d(%d) -> %d %d\n " , pNode -> iData, pNode -> iHeight, pNode -> pLeft -> iData, pNode -> pRight -> iData);
            que.Enqueue(pNode -> pLeft);
            que.Enqueue(pNode -> pRight);
        }
         else   if (pNode -> pLeft != 0 )
        {
            que.Enqueue(pNode -> pLeft);
            printf( " %d(%d) -> %d x\n " , pNode -> iData, pNode -> iHeight, pNode -> pLeft -> iData);
        }
         else   if (pNode -> pRight != 0 )
        {
            que.Enqueue(pNode -> pRight);
            printf( " %d(%d) -> x %d\n " , pNode -> iData, pNode -> iHeight, pNode -> pRight -> iData);
        }
    }
}

#endif

//  Main
//
int  main( int  argc,  char *  argv[])
{
    CAVLTree avl;
    avl.Insert( 14 );
    avl.Insert( 11 );
    avl.Insert( 13 );
    avl.Insert( 1 );
    avl.Insert( 4 );
    avl.Insert( 3 );
    avl.Insert( 15 );
    avl.Insert( 2 );
    avl.Insert( 9 );
    avl.Insert( 10 );
    avl.Insert( 8 );
    avl.Insert( 7 );

    avl.Delete( 10 );
    avl.Delete( 8 );
    avl.Delete( 7 );
    avl.Delete( 13 );
#ifdef _DEBUG
    avl.PrintTree();
#endif

     return   0 ;
}

代码中有些注释显示得不太正常，这是因为这个博客中的代码部分不适用等宽字符的缘故，拿到你的IDE下看就正常了。

转自：http://www.cppblog.com/guogangj/archive/2009/10/26/99502.html