第四章 复平面
这一章强烈推荐去看B站上的3Blue1Brown的欧拉公式和初等群论这一节,用几何语言来讲述欧拉公式的形成,尤其是用极为精彩的方法解释了为什么以e为底数。网址如下
https://www.bilibili.com/video/av11339177/ 点击打开链接
4.1简介
某些学科的历史常常使人兴奋不已,尤其是在对日期或现有艺术有争议时。澄清谁在别人之前做了什么事,是历史学家的工作,他们可以帮助弄清谁该为某一事件负责,谁应该取得功劳。从文献、书籍和私人信件解开事件,并将它们放置在一个公正的位置,需要学科知识客观的分析。
对于大多数研究学科来说,两个日期在确定优先顺序中中是非常重要的:一份论文提交出版的日期,以及一份已发表论文的发表日期。,假设有一个高效的邮政系统,一个公正的同侪审查制度,以及其他许多,这样的协议似乎是一个公平的计划
在数学和科学中,一些研究者并不总是有信心发布一个新的想法,如果没有发表,这个想法要么留在他们的脑中,要么放在笔记本上,可能在研究人员死后被发现。不幸的是,对于历史学家来说,人类的头脑并不是一个方便的信息储存库!
4.2一些历史
关于复平面的一些历史就不翻译了。
4.3复平面
和复数发展有关的人中就有伟大的瑞士数学家欧拉,欧拉证明了定义
eiθ= cosθ + i sinθ
并且当θ = π时,就会出现数学中最完美的公式之一:
eiπ= −1 或 eiπ + 1 = 0
其中包括了5个最重要的的常数:0,1.e. π和i,和最基础的运算:加法,乘法和幂。
当θ = π/2时会出现其他结果:
eiπ/2 = cos π/2+ i sinπ/2= i
因此
ii = (eiπ/2)i= ei2π/2=e−π/2= 0.207879576...
说明了虚数的单位元可以和他自己运算产生实数!
在3章我们看到,i的幂产生两个序列(1,i,-1,-i,1,…)和(1,−i,−1,i,1,…),这和一个笛卡尔坐标轴顺时针和逆时针方向产生的旋转序列(x,y,−x,−y,x,…)和(x,-y,−x,y,x,…)有惊人的相似之处。这种相似性不是巧合,因为复数属于一个叫做复平面的二维平面,我们现在将描述它。
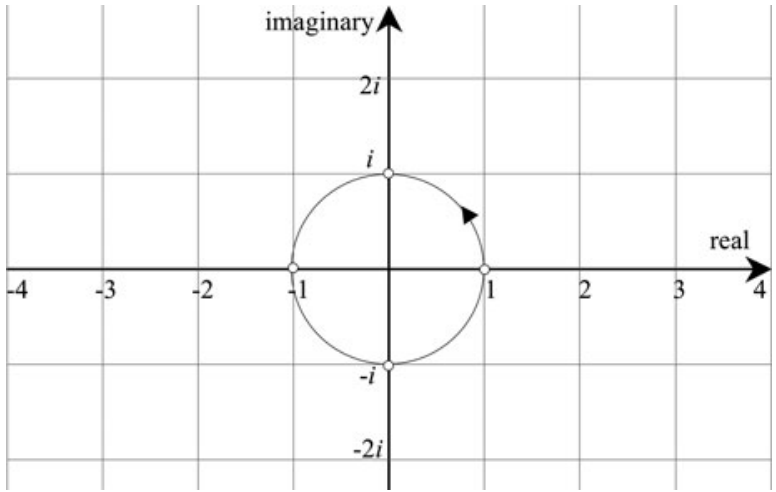
图1 复平面和单位圆
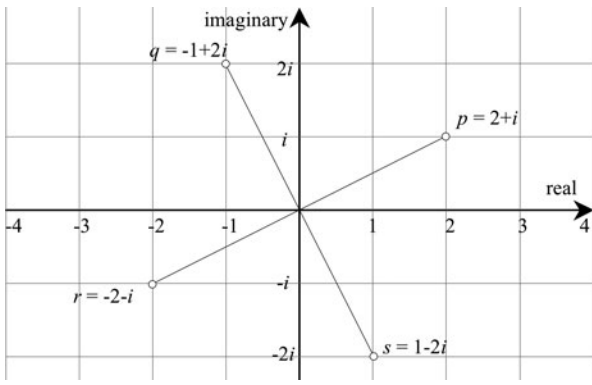
复平面上使我们能够将复数映射为横轴记录实数部分,与纵轴记录的虚数部分,如图4.1所示。该图还显示了一个单位圆,它依次通过1,i,−1,−i,这些i的幂,这表明乘一个i相当于旋转90°。为了演示这种旋转效果,图4.2显示了四个复数的复平面:
p = 2 + i,q = 1 +−2i,r =−2−i,s = 1−2i
他们之间相距90度。
有四个复数的复平面
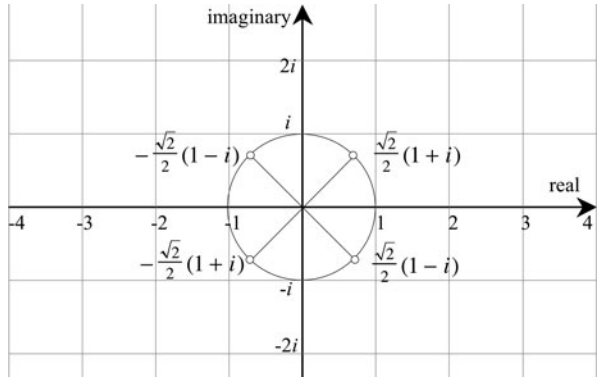
√i相当于旋转45°
4.4极坐标表示
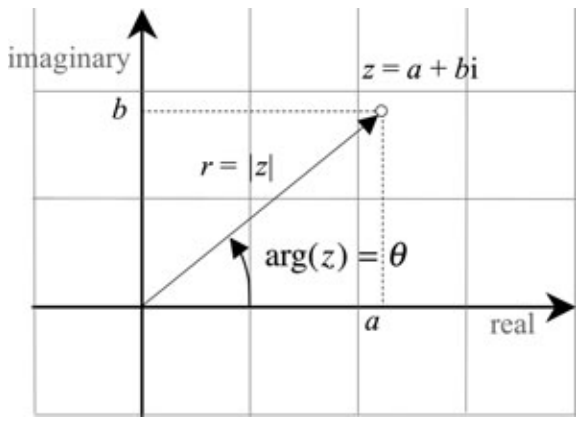
一个复数的极坐标表示
线长r,又称幅值为
r = |z| = √(a2 + b2)
和实轴之间的夹角为
arg(z) = θ 其中 tanθ = b/a
按如下规则计算
第一象限 a > 0, b > 0 θ =arctan(b/a)
第二、三象限 a < 0 θ = arctan(b/a) + π
第四象限 a > 0, b < 0 θ = arctan(b/a) + 2π
因此我们可以将复数写为
z = a + bi= r cosθ + ri sinθ= r(cosθ + i sinθ).
根据欧拉的发现可得
eiθ = cosθ + i sinθ
因此可以写出
z = reiθ
因此当我们有如下两个复数
z = reiθ
w = seiφ
他们的乘积为
zw = rseiθeiφ= rsei(θ+φ)=rs[cos(θ + φ) + i sin(θ + φ)].
幅值|zw| = rs,夹角arg(zw) = θ + φ
除法类似,不再赘述。
4.5旋转
从上述研究中可以发现,z = reiθ的模是r, w = seiφ的模是s,他们之间相乘出的第三个复数模是rs,无法描述描述旋转,因此,为了避免这种情况,z,w的模必须是单位元,在这种条件下才能表示旋转。
任何复数乘以eiθ相当于旋转θ角。
复数x+yi旋转θ角也可以表示为
x’ + y’i = (cosθ + i sinθ)(x + yi)= x cosθ − y sinθ + i(x sinθ + ycosθ)
他的矩阵形式为
[x’,-y’; y’, x’]= [cosθ ,-sinθ; sinθ,cosθ] [x ,-y; y, x]
因此我们定义旋转复数Rθ和他的共轭Rθ*
Rθ=cosθ + i sinθ,表示顺时针旋转θ°
Rθ*=cosθ +-i sinθ,表示逆时针旋转θ°
4.6总结
在这一章中,我们发现了复数平面的图形解释。欧拉公式eiθ=cosθ+isinθ允许我们表达复数的虚数幂,从而使我们能够计算乘法和除法更容易。总的来说,这些想法都是带领我们走向一个旋转的理念,这会发展为采用四元数。
4.6.1运算总结

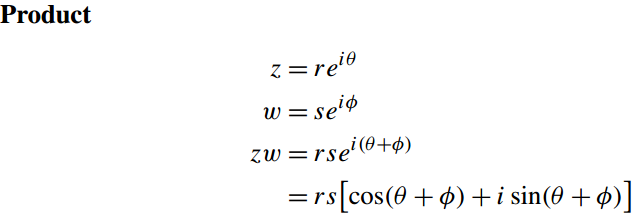
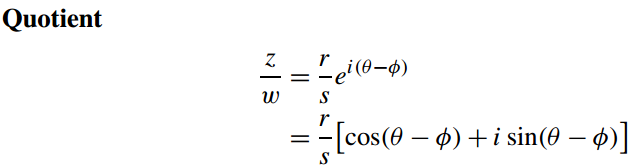
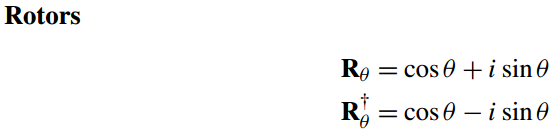




















 490
490











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








