经验风险最小化(Empirical Risk Minization,ERM)

一、偏差方差权衡

1. 偏差与方差

     回顾之前在讨论线性回归问题时，通常存在以下三种情况：

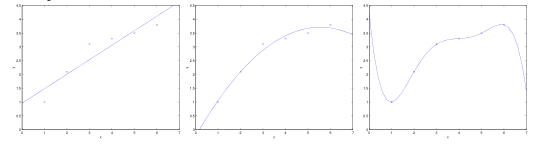
• 图1，用一条直线拟合一个呈现二次结构的散点，无论训练样本怎样增多，一次函数都无法准确地表示出二次函数。我们认为它具有高偏差（high bias），表现出欠拟合（underfit）。
• 图3，用一条五次多项式函数来拟合数据，对于数据的结果，得到的仍然不是一个好的模型，算法拟合出了数据中的一些奇怪规律。我们认为它具有高方差（high variance），表现出过拟合（overfit）。
• 图2，用一条二次函数来拟合数据，很显然能够匹配数据集合的一般规律。

     偏差与方差之间存在某种平衡。如果模型过于简单且参数较少，它可能有高偏差（低方差）；相反，如果模型过于复杂且参数众多，它可能有高方差（低偏差）。它们之间究竟存在怎样的关系呢？为了说明这个问题，先要提出一个更为一般的机器学习模型——经验风险最小化，在正式介绍该模型之前，需要对两个引理有所了解来帮助理解。

 

2. 两个引理

   为了解释偏差方差权衡现象，需要引出两个引理：联合界引理和Hoeffding不等式。

 （1）联合界引理

  

    这个引理常作为概率论的公理，k个事件中任意事件发生的概率最多为每个事件独立发生的概率之和。其中，事件可能发生，也可能不发生。

 （2）Hoeffding不等式

   

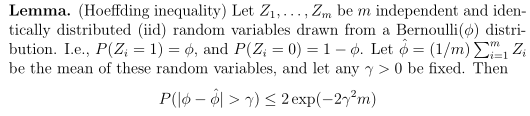
     这个引理在学习理论中也称为Chernoff边界（Chernoff bound），给出了一种估计伯努利随机变量均值时，错误概率的上界。关于这个上界有个很有意思的结论：随着样本数目m增大，高斯分布的凸性会随之收缩，也就是高斯分布的尾部会变小，中间隆起。举个例子，当你投掷一枚两面的硬币，人像面朝上的概率为Φ，在投掷m次（m足够大）后，计算人像面朝上的次数是一种很好的估计Φ值的方法。

 

3. 两个误差

    介绍两个学习理论中十分重要的概念：训练误差与一般误差。

 （1）训练误差

    考虑二元分类y∈{0,1}，给定训练集合S={(x⁽ⁱ⁾,y⁽ⁱ⁾);i=1,2,...,m}，训练样本服从独立同分布D，对于一个假设函数h，我们定义训练误差（Training error），也叫作经验风险（empirical risk）或经验误差（empirical error）：

   

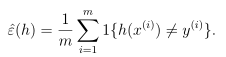
 （2）一般误差

   一般误差（Generation error）定义为：

 

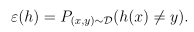
   它表示当从服从分布D的样本集合中取出一个样本(x,y)，假设函数h将会分类错误的概率。