二叉搜索树的查询、插入与删除操作（Binary Search Tree, Search, Insert, Delete）（C++）

一、概念

    设 x 是二叉搜索树中的一个结点。如果 y 是 x 左子树中的一个结点，那么 y.key ≦ x.key。如果 y 是 x 右子树中的一个结点，那么 y.key ≧ x.key。

    为了便于描述，我们按如下方式定义树结点：

struct TreeNode
{
    int key;
    TreeNode* left;
    TreeNode* right;
    TreeNode* parent;

    TreeNode(int key, TreeNode* left = nullptr, TreeNode* right = nullptr, TreeNode* parent = nullptr)
    : key(key)
    , left(left)
    , right(right)
    , parent(parent)
    {}
};

二、查询二叉搜索树

    二叉搜索树的查询操作包括 Search, Minimum, Maximum, Successor, Predecessor，在任何高度为 h 的二叉搜索树上，所有的查询操作时间复杂度均为 O(h)。

1. 查找

    输入一个指向树根结点的指针与一个关键字 key ，如果此节点存在，则返回一个指向关键字 key 的结点的指针，否则返回 null。递归与迭代版本分别如下：

TreeNode* treeSearch(TreeNode* root, int key)
{
    if(root == nullptr || key == root->key){
        return root;
    }

    if(key < root->key){
        return treeSearch(root->left, key);
    }else{
        return treeSearch(root->right, key);
    }
}

TreeNode* iterativeTreeSearch(TreeNode* root, int key)
{
    while(root && key != root->key){
        if(key < root->key){
            root = root->left;
        }else{
            root = root->right;
        }
    }

    return root;
}

2. 最大关键字与最小关键字

    通过从树根开始沿着 left 孩子指针直到遇到一个 null，我们可以得到最小元素，反之可以得到最大元素。

TreeNode* treeMinimum(TreeNode* root)
{
    while(root->left){
        root = root->left;
    }

    return root;
}

TreeNode* treeMaximum(TreeNode* root)
{
    while(root->right){
        root = root->right;
    }

    return root;
}

3. 后继与前驱

    一个结点 x 的后继是大于 x.key 的最小关键字的结点，前驱概念与之对称。

TreeNode* treeSuccessor(TreeNode* node)
{
    if(node->right){
        return treeMinimum(node->right);
    }

    TreeNode* y = node->parent;

    while(y && node == y->right){
        node = y;
        y = y->parent;
    }

    return y;
}

TreeNode* treePredecessor(TreeNode* node)
{
    if(node->left){
        return treeMaximum(node->left);
    }

    TreeNode* y = node->parent;

    while(y && node == y->left){
        node = y;
        y = y->parent;
    }

    return y;
}

三、插入和删除

1. 插入

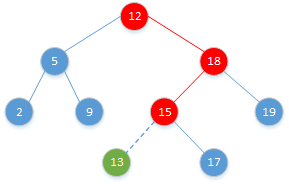
    插入新元素后要保证二叉搜索树性质仍然成立，下图展示了元素 13 插入树的整个过程，红色代表从树根开始向下插入到数据项位置的简单路径，虚线表示了为插入数据项而加入的树中的一条链。

 

代码如下：

void treeInsert(TreeNode* root, TreeNode* node)
{
    TreeNode* y = nullptr;
    TreeNode* x = root;

    while(x){
        y = x;

        if(node->key < x->key){
            x = x->left;
        }else{
            x = x->right;
        }
    }

    node->parent = y;

    if(y == nullptr){
        root = node;
    }else if(node->key < y->key){
        y->left = node;
    }else{
        y->right = node;
    }
}

2. 删除

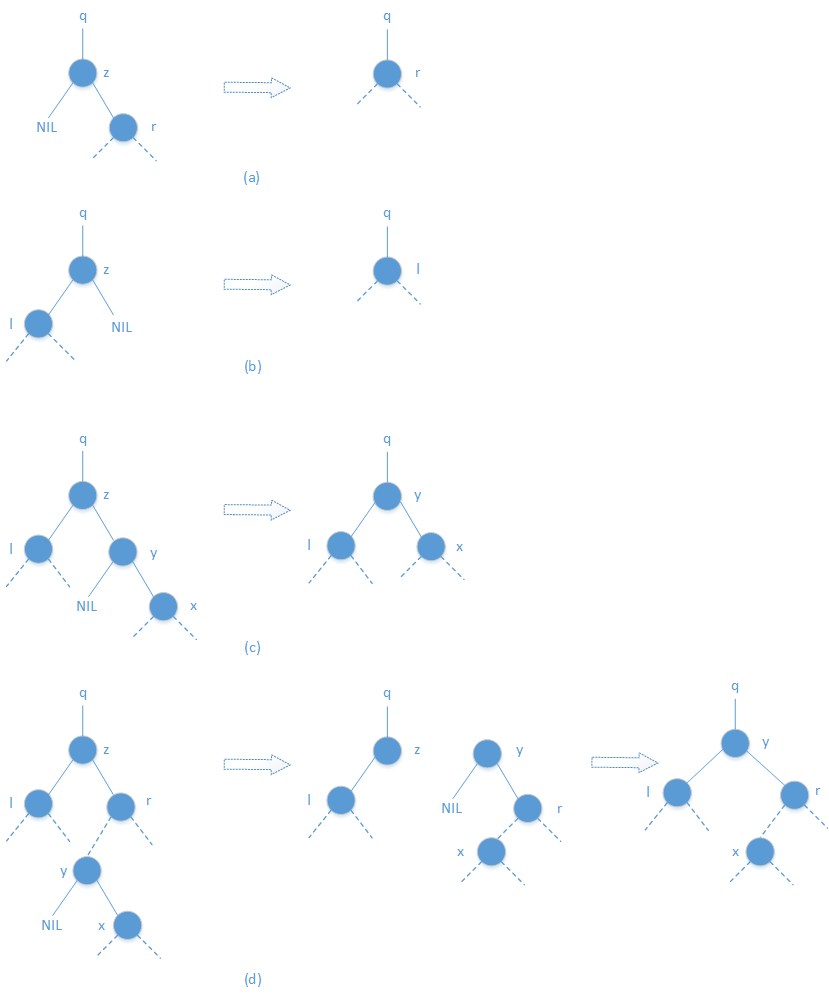
    删除操作较插入操作繁琐，大致分为四种情况，如下图所示：

    （a）结点 z 没有左孩子，用其右孩子 r 来替换 z，其中 r 可以是 NIL，也可以不是；

   （b）结点 z 有一个左孩子 l 但没有右孩子，用 l 来替换 z；

   （c）结点 z 有两个孩子，其左孩子是结点 l，其右孩子 y 还是其后继，y 的右孩子是结点 x，用 y 替换 z，修改使 l 成为 y 的左孩子，但保留 x 仍为 y 的右孩子；

   （d）结点 z 有两个孩子（左孩子 l，右孩子 r），并且 z 的后继 y ≠ r 位于以 r 为根的子树中，用 y 自己的右孩子 x 来代换 y，并且置 y 为 r 的双亲，然后，再置 y 为 q 的孩子和 l 的双亲。

    为了在二叉搜索树内移动子树，定义一个子过程 Transpalnt，它是用一棵子树替换一棵子树并成为其双亲的孩子结点，当 Transplant 用一棵以 v 为根的子树来替换一棵以 u 为根的子树时，结点 u 的双亲就变为 v 的双亲，并且最后 v 成为 u 的双亲的相应孩子。其代码如下：

void transplant(TreeNode* root, TreeNode* oldNode, TreeNode* newNode)
{
    if(oldNode->parent == nullptr){
        root = newNode;
    }else if(oldNode == oldNode->parent->left){
        oldNode->parent->left = newNode;
    }else{
        oldNode->parent->right = newNode;
    }

    if(newNode){
        newNode->parent = oldNode->parent;
    }
}

于是整个删除过程如下所示：

void treeDelete(TreeNode* root, TreeNode* node)
{
    if(node->left == nullptr){
        transplant(root, node, node->right);
    }else if(node->right == nullptr){
        transplant(root, node, node->left);
    }else{
        TreeNode* y = treeMinimum(node->right);

        if(y->parent != node){
            transplant(root, y, y->right);
            y->right = node->right;
            y->right->parent = y;
        }

        transplant(root, node, y);
        y->left = node->left;
        y->left->parent = y;
    }
}