到目前为止,我们已经见到了一个回归的例子和一个分类的例子。在回归的例子里,我们有



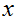

8 指数族
为了走进GLMs,我们将会以定义指数族分布作为开始。我们说一类分布在指数族如果它能被写成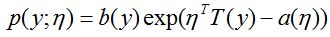
这样的形式。这里,
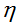 被称作分布的自然参数(natural parameter)(也称作典范参数(canonical parameter));
被称作分布的自然参数(natural parameter)(也称作典范参数(canonical parameter)); 被称作充分统计量(sufficient
statistic)(对于我们考虑的分布,情况经常是
被称作充分统计量(sufficient
statistic)(对于我们考虑的分布,情况经常是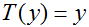 );
);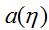 是log 配分函数(log partition function)。
是log 配分函数(log partition function)。 本质上在归一化常数发挥了作用,确保了
本质上在归一化常数发挥了作用,确保了 分布关于
分布关于 的和或积分是1。
的和或积分是1。一个固定的
 定义了一个以
定义了一个以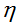 作为参数的分布族(集合)。当我们改变
作为参数的分布族(集合)。当我们改变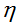 ,我们然后得到这个族中不同的分布。
,我们然后得到这个族中不同的分布。我们现在证明伯努利和高斯分布式指数族分布的例子。均值为
 的伯努利分布,写作Bernoulli(
的伯努利分布,写作Bernoulli( ),指定了一个
),指定了一个 的分布,使得
的分布,使得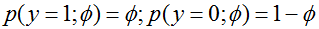 。当我们改变
。当我们改变 ,我们得到不同均值的伯努利分布。我们现在证明这类通过改变
,我们得到不同均值的伯努利分布。我们现在证明这类通过改变 得到的伯努利分布在指数族中;也就是,存在关于
得到的伯努利分布在指数族中;也就是,存在关于 的选择使得
的选择使得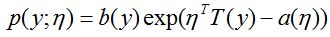
完全变成这类伯努利分布。
我们把伯努利分布写作:
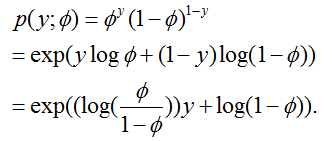
因此,自然参数
 。有趣地是,如果我们根据
。有趣地是,如果我们根据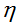 解得
解得 来求
来求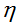 的反函数,我们得到
的反函数,我们得到 。这是类sigmoid函数。为了完成伯努利分布作为一个指数族分布的公式化表述,我们也有
。这是类sigmoid函数。为了完成伯努利分布作为一个指数族分布的公式化表述,我们也有
这证明了伯努利分布通过选择合适的
 可以写成
可以写成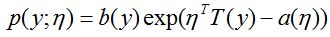
的形式。
现在让我们继续考虑高斯分布。回想一下,当推导线性回归时,
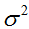 的值对我们最后对值
的值对我们最后对值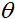 和
和 的选择无关。因此,我们可以选择一个随意的
的选择无关。因此,我们可以选择一个随意的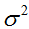 值,而不会改变任何事情。为了简化下面的推导,让我们令
值,而不会改变任何事情。为了简化下面的推导,让我们令 。我们然后有:
。我们然后有:
因此,我们可以看到高斯分布属于指数族,并且
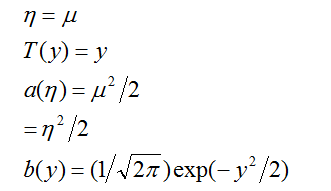
还有很多其他的属于指数族的分布:多项式分布(我们稍后会看到),泊松分布(用于计数建模;也看下习题集);伽马分布和指数分布(用来建模连续的,非负的随机变量,比如时间间隔);贝塔分布和狄利克雷分布(概率分布),还有更多的;在下节中,我们将会描述一个构建模型的一般“配方”,在模型中,
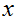

假定你想基于某些特征
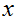 ,比如商店的推广、过去的广告、天气、一周的哪一天等,来构建一个模型来估计在任何给定时间内到你商店客人的数量
,比如商店的推广、过去的广告、天气、一周的哪一天等,来构建一个模型来估计在任何给定时间内到你商店客人的数量 (或你网站的浏览量
(或你网站的浏览量 )。我们知道泊松分布通常是一个好的构建参观者数量的模型。知道了这些,我们如何为我们的问题提出一个模型?幸运的是,泊松分布是一个指数族分布,所以我们可以应用一个广义线性模型(GLM)。在这节中,我们将会描述一个构造用来解决诸如此类问题的GLM模型的方法。
)。我们知道泊松分布通常是一个好的构建参观者数量的模型。知道了这些,我们如何为我们的问题提出一个模型?幸运的是,泊松分布是一个指数族分布,所以我们可以应用一个广义线性模型(GLM)。在这节中,我们将会描述一个构造用来解决诸如此类问题的GLM模型的方法。一般地说,考虑一个分类或者回归问题,在这些问题中,我们想预测一些作为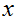

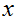

 。也就是,给定
。也就是,给定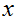 和
和 ,
, 的分布服从某个参数为
的分布服从某个参数为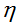 的指数族分布。
的指数族分布。2.给定
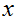 ,我们的目标是预测给定
,我们的目标是预测给定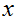 时的
时的 的期望值。在我们大多数例子中,我们有
的期望值。在我们大多数例子中,我们有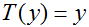 ,所以这意味着我们通过学习好的满足
,所以这意味着我们通过学习好的满足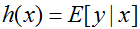 的假设
的假设 来得到预测值
来得到预测值 的输出值。(注意这个假设在逻辑回归和线性回归中选择
的输出值。(注意这个假设在逻辑回归和线性回归中选择 时都是满足的,比如,在逻辑回归中,我们有
时都是满足的,比如,在逻辑回归中,我们有 )
)3.自然参数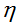
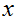

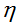

 的分布建模是经常非常有效的;比如,我们马上证明一下逻辑回归和普通最小二乘都可以由GMLs推导得到。
的分布建模是经常非常有效的;比如,我们马上证明一下逻辑回归和普通最小二乘都可以由GMLs推导得到。9.1 普通最小二乘
为了证明普通最小二乘是GML族的一个特殊情况,考虑这样的环境,目标变量
 (在GML术语里也被称作反映变量(response variable))是连续的,我们为给定
(在GML术语里也被称作反映变量(response variable))是连续的,我们为给定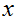 下的
下的 的条件分布建模为高斯分布
的条件分布建模为高斯分布 。(这里,
。(这里, 可能依赖
可能依赖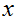 )。所以,我们让上面以
)。所以,我们让上面以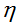 为参数的指数族表示成一个高斯分布。像我们之前看到的,在高斯分布作为一个指数族分布的公式化里,我们有
为参数的指数族表示成一个高斯分布。像我们之前看到的,在高斯分布作为一个指数族分布的公式化里,我们有 。所以,我们有
。所以,我们有
第一个等式由假设2给出;第二个等式由
 得出,所以它的期望值为
得出,所以它的期望值为 。
。第三个等式由假设1(我们之前的推导证明了在高斯分布作为一个指数族分布的公式化表示时有
我们现在考虑逻辑回归。这里我们对二值分类有兴趣,所以
 。假定
。假定 是二值的,因此选择伯努利分布族来建模给定下
是二值的,因此选择伯努利分布族来建模给定下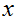 的
的 的条件分布看起来是自然的。在我们伯努利分布表述为指数族分布的公式化中,我们有
的条件分布看起来是自然的。在我们伯努利分布表述为指数族分布的公式化中,我们有 。而且,注意到如果
。而且,注意到如果 服从以
服从以 为参数的伯努利分布。所以,按照类似普通最小二乘的推导,我们得到:
为参数的伯努利分布。所以,按照类似普通最小二乘的推导,我们得到:
所以,这给出了形式为

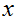

多介绍一点术语,以自然参数为自变量的函数



让我们再看一个GLM的例子。考虑一个分类问题,在这个分类问题中,反应变量
 可以取k个值里的任何一个,所以
可以取k个值里的任何一个,所以 。比如说,我们想把邮件分成3类,诸如垃圾邮件,个人邮件和工作相关邮件,而不是把它分成垃圾邮件和非垃圾邮件两类——这是二值分类问题。回应变量仍旧是离散的,但是可以取超过两个值。因此我们将根据多项式分布来建模。
。比如说,我们想把邮件分成3类,诸如垃圾邮件,个人邮件和工作相关邮件,而不是把它分成垃圾邮件和非垃圾邮件两类——这是二值分类问题。回应变量仍旧是离散的,但是可以取超过两个值。因此我们将根据多项式分布来建模。让我们堆到一个为这种多项式数据建模的GLM。为了做这个,我们将先从把多项式分布表示成指数族分布开始。
为了参数化一个有k个可能输出结果的多项式分布,我们可以使用k个参数
 指定每个输出结果的概率。然而,这些参数是冗余的,或更正式地说,它们不是独立的(因为知道了任何k-1个参数
指定每个输出结果的概率。然而,这些参数是冗余的,或更正式地说,它们不是独立的(因为知道了任何k-1个参数 唯一的决定了最后一个参数,因为它们必须满足
唯一的决定了最后一个参数,因为它们必须满足 )。所以,我们转而只使用k-1个参数
)。所以,我们转而只使用k-1个参数 来参数化多项式分布,在这里
来参数化多项式分布,在这里 。为了符号上的方便,我们也令
。为了符号上的方便,我们也令 ,但我们应该记住这不是一个参数,它完全由
,但我们应该记住这不是一个参数,它完全由 来指定。
来指定。为了把这个多项式分布表示一个指数族分布,我们将定义
 如下:
如下:
不像我们以前的例子,这里我们不再有
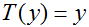 ;并且,
;并且, 是一个k-1维的向量,而不是一个实数。我们将用
是一个k-1维的向量,而不是一个实数。我们将用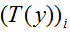 来表示向量
来表示向量 的第i个元素。
的第i个元素。我们再介绍一个非常有用的符号。知识函数1{·}值为1如果它的参数是真的,否则是0(1{True}=1,1{False}=0)。比如,1{2=3}=0,1{3=5-2}=1。所以,我们也可以把
 和
和 的关系写作
的关系写作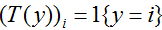 。(在你继续往下读之前,确保你理解了为什么这是正确的!)而且,我们有
。(在你继续往下读之前,确保你理解了为什么这是正确的!)而且,我们有 。
。我们现在准备证明多项式分布是一个指数族分布。我们有:
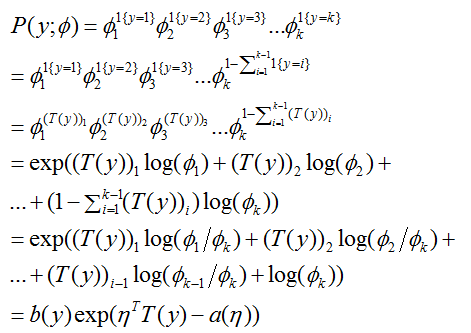
这里
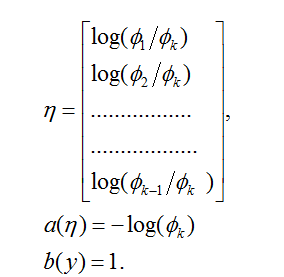
这完成了我们的多项式分布作为指数族分布的公式化表示。
连接函数由
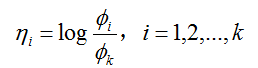
给出。为了方便,我们也定义了
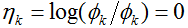 。为了反解连接函数,推导出反应函数,我们因此有
。为了反解连接函数,推导出反应函数,我们因此有
这表明
这个从
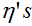 映射到
映射到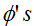 的函数被称作softmax函数。
的函数被称作softmax函数。为了完成我们的模型,我们使用之前给出的假设3,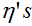
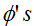




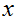

给出。
这个(应用到
 分类问题的)模型被称作softmax回归。它是逻辑回归的一个推广。
分类问题的)模型被称作softmax回归。它是逻辑回归的一个推广。我们的假设将输出

换句话说,我们的假设将会输出i=1,2,...,k中的每一个i值的估计概率
 。(尽管上面的
。(尽管上面的 只是k-1维的,但是很显然
只是k-1维的,但是很显然 可以通过
可以通过 得到。)
得到。)最后,让我们讨论参数拟合。类似于我们原来普通最小二乘和逻辑回归的推导,如果我们有一个m个样例的训练集
 ,并想学习这个模型的参数
,并想学习这个模型的参数 ,我们首先写下log似然性
,我们首先写下log似然性
为了得到上式中的第二行,我们使用了等式(*)中的

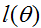
 广义线性模型概览
广义线性模型概览





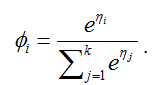

















 1018
1018

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








