对于一颗普通的高度为h的二叉查找树,对诸如locate、predecessor、successor、minimum、maximum、insert、erase等基本操作的时间复杂度一般都为O(h),这样,在树高较低时,这些操作实行就会很快。但是,经过长期的插入和删除后,树高可能发生较大变化,极端情况下甚至退化为链状,此时树高为O(n),那么上述操作的性能将大大降低。而红黑树作为一种加入了平衡策略的二叉查找树,能够保证即使在最坏情况下,上述操作也能够在O(h)时间完成。
红黑树的性质
红黑树是一种二叉查找树,和一般查找树所不同的是,它的每个节点都被标以了颜色,为黑(Black)或者红(Red)。通过对任一条从根到叶子节点上的着色方式,或者说黑节点出现数量的限制,保证了没有一条路径的长度会比其他任何路径长出两倍,因而接近平衡。
结合前面提高的普通的二叉查找树,我们可以很容易直到红黑树的节点包括五个域:color、left、right、parent、key,如果一个节点没有孩子或者父亲,那么给指针域将指向NULL。我们把NULL称为外节点,而把其他带有关键字的节点称为内节点。
其节点结构如下:
template <typename T>
class node
{
private:
friend class RBTree<T>;
node *parent;
node *left;
node *right;
T key;
COLOR color;
node(){}//默认构造函数,只供创建nil时调用
public:
node(const T &k, COLOR c = red) :key(k), color(c),
parent(NULL), left(NULL), right(NULL){}
T& getKey(){ return key; }
const T& getKey()const { return key; }
};满足下面五条性质的二叉查找树即可称为红黑树:
1) 每个节点要么是红的,要么是黑的;
2) 根节点是黑色的;
3) 每个叶节点,即NIL是黑色的;
4) 如果一个节点是红色的,那么它的两个孩子必须是黑的;
5) 对于每个节点,从该节点到其子孙节点的所有路径上包含相同数目的黑节点。
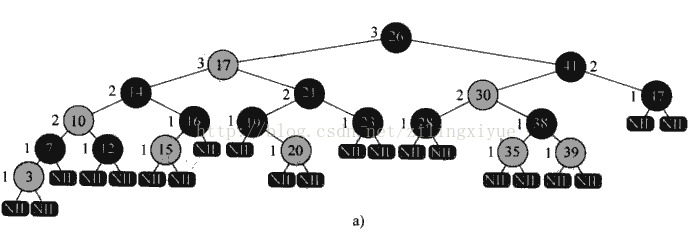
下图是一颗红黑树的例子:
为了便于实现以及处理相关的边界条件,我们采用一个哨兵nil来代替NULL,nil也是一个红黑树节点,且颜色为黑,其他指针和关键域可以设为任意值,所有指向NULL的指针都将指向它,包括根节点的父指针域。作此约定之后上述红黑如下:
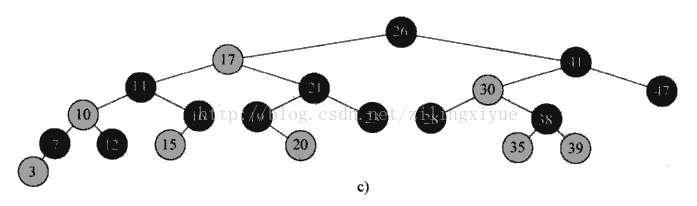
如果省略掉所有的叶子nil,红黑树呈现如下,后面的图中我们都采用下述画法:
黑高度:从某个节点x出发(不包括该节点)到达一个叶节点的任一条路径上的黑节点的数目成为该节点的黑高度,用bh(x)表示;根节点的黑高度定义为整棵红黑树的黑高度。
前面我们有说,红黑树能够保证即使在最坏情况情况下,上述动态集合操作也能在O(h)时间内完成,现在我们来证明一个定理:
一棵有n个内节点的红黑树的高度最多为2lg(n+1)。
证明如下:
红黑树的操作
1、旋转
当我们做一些修改红黑树结构的操作(如insert、erase)之后,红黑树的性质有可能收到了破坏。那么,为了能够恢复这些性质,就有必要对树做一些调整,这是通过旋转来实现的,旋转分为左旋和右旋,我们主要介绍左旋,右旋和左旋对称。
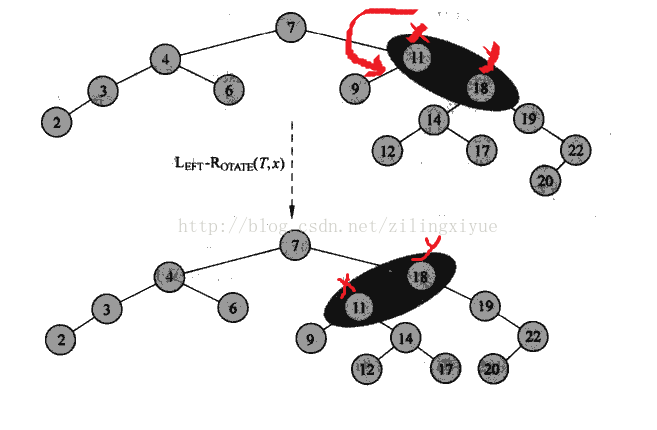
下图给出了两种旋转。当我们在某个节点x做左旋时,首先需要判断它的右孩子y是否存在,即是否指向nil,毕竟只有右孩子存在时才能进行左旋。左旋以x和y之间的链为“支轴”做逆时针旋转。从而使得y成为该子树的新根,x成为y的左孩子,而y的左子树则成为x的右子树。
以下是左旋的伪代码:
leftRotate(T, x)
{
if (right[x] != nil)
{
y <- right[x];//设置y
right[x] <- left[y];//y的左子树成为x的右子树
if (left[x] != nil)
parent[left[y]] <- x;
parent[y] <- parent[x];//将x的父节点设为y的父节点
if (parent[x] != nil)
root[T] <- y;
else if (x == left[parent[x]])
left[parent[x]] <- y;
else right[parent[x]] <- y;
left[y] <- x;//x成为y的左节点
parent[x] <- y;
}
}下图显示了旋转的操作过程。两种旋转都可以在O(1)时间内完成,因为旋转过程中,只有相关节点的指针域被修改,其他域和节点均保持不变。
2、插入
红黑树的插入过程类似于普通二叉查找树,插入过程运行时间O(h)。下面是插入伪代码:
insert(T, z)
{
y <- nil;
x <- root[T];
while (x != nil)
{
y <- x;
if (key[z] < key[x])
x <- left[x];
else x <- right[x];
}
parent[z] <- y;
if (y == nil)
root[T] <- z;
else if (key[z] < key[y])
left[y] <- z;
right[y] <- z;
left[z] <- nil;
right[z] <- nil;
color[z] <- red;
insertFixup(T, z);
}
对比普通的二叉查找树的插入,红黑树的插入有四点不同:
1) 在和红黑树的插入中所有的NULL都被换为了nil;
2) left[z]和right[z]都被设置为nil,以保持树的结构;
3) 插入节点被标为红色;
4) 因为插入红色的节点z可能导致某些性质被破坏,故需要调用insertFixup进行调整。
下面是插入调整的伪代码:
insertFixup(T, z)
{
while (color[parent[z]] == red)
{
if (parent[z] == left[parent[parent[z]]])
{
y <- right[parent[parent[z]]];
if (y != nil && color[y] == red)
{//情况1
color[parent[z]] <- black;
color[y] <- black;
color[parent[parent[z]]] <- red;
z <- parent[parent[z]];
}
else if (z == right[parent[z]])
{//情况2
z <- parent[z];
leftRotate(T, z);
}
color[parent[z]] <- black;//情况3
color[parent[parent[z]]] <- red;
rightRotate(T, parent[parent[z]]);
else //与第一个if (parent[z] == left[parent[parent[z]]])对称
//只需将这个if语句所有的left换成right即可
}
}
color[root[T]] <- black;
}
为了理解insertFixup的工作过程,我们必须要知道该过程可能会破坏那些性质。性质1和性质3可以继续保持,因为新插入节点的子女均为哨兵nil;性质5,即从一个指定节点到叶子节点的黑色节点树木都相等,这个当然也会保持,因为新插入节点标示的是红色(Red);因此唯一可能被破坏的就是性质2——根节点必须为黑色以及性质4——红色节点不能够有红色子女。
对于每一次的while循环开始有:
1) 节点z是红色;
2) 如果parent[z]是根,则parent[z]是黑色;
3) 如果有红黑性质被破坏,则之多有一个被破坏,不是性质2就是性质4.因为如果违反了性质2,则因为z是根且z是红色;如果违法了性质4,则因为z和parent[z]均为红色。
关于while的条件,我们没有判断z的父节点parent[z]是否存在,实际上是存在的。因为根据循环体的2) 部分如果parent[z]是根部,则parent[z]必定是黑色的,否则在插入调整前红黑树已经就被破坏了。然而我们只有在parent[z]是红色时才进入循环体,所以可以推断parent[z]不可能是根,所以parent[parent[z]]必然存在。
从伪代码可以看出,总共有6中情况,但是由于左右子树对称,只用分析其中三种即可,对于具体的分析过程,可以参考《算法导论》或者维基百科_红黑树。下面列出可能的三种情况以及图解和对应代码:
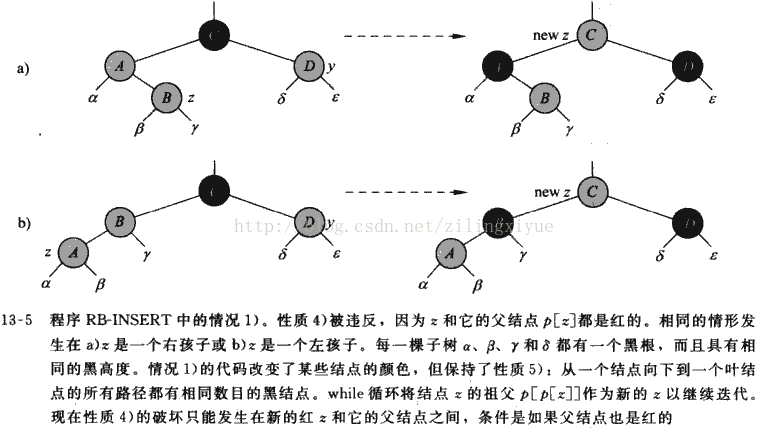
情况1):z的叔叔y是红色的
伪代码:
if (y != nil && color[y] == red)
{//情况1
color[parent[z]] <- black;
color[y] <- black;
color[parent[parent[z]]] <- red;
z <- parent[parent[z]];
}
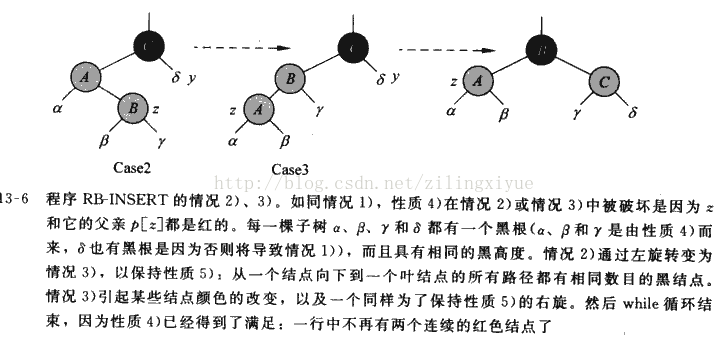
情况2):z的叔叔y是黑色的,而z是其父节点的右孩子
情况3):z的叔叔y 是黑色的,而且z是左孩子
伪代码:
else if (z == right[parent[z]])
{//情况2
z <- parent[z];
leftRotate(T, z);
}
color[parent[z]] <- black;//情况3
color[parent[parent[z]]] <- red;
rightRotate(T, parent[parent[z]]);
可以看出,策略就是将情况1或者情况2不断向情况3调整,最终是问题得到解决。
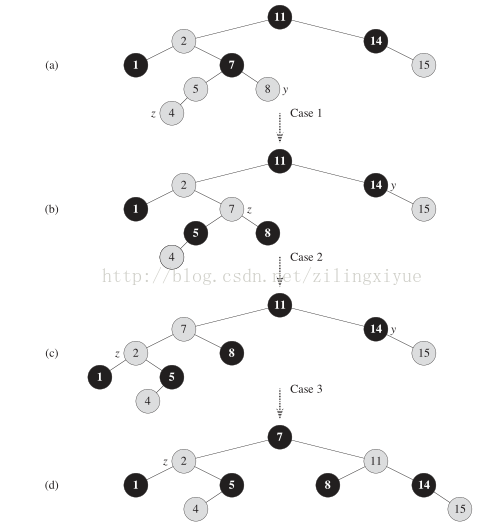
下图显示了insertFixup在一棵红黑树上连续操作的例子以加深理解(注意:《算法导论》中文第二版此处第三幅图画错了,并且我对比后来的第三版确认第二版确实有误,下图正解):
2、删除
同红黑树的插入类似,它的删除过程前大部分依然和普通二叉查找树的删除类似。在执行节点的删除之后会调用一个辅助程序eraseFixup来调整树的结构,以保持红黑性质。下面是删除的伪代码:
erase(T, z)
{
if (left[z] == nil && right[z] == nil)
y < -z;
else y < -successor(z);
if (left[z] != nil)
x < -left[z];
else x < -right[z];
parent[x] < -parent[y];
if (parent[y] == nil)
root[T] < -x;
else if (y == left[parent[y]])
left[parent[y]] < -x;
else right[parent[y]] < -x;
if (y != z)
key[z] < ->key[y];
if (color[y] == black)
eraseFixup(T, x);
return y;
}同理,对比普通二叉查找树的删除过程,红黑树的删除也有三点不同:
1) 将所有对NULL的引用都替换成了哨兵nil;
2) 在执行parent[x] < -parent[y];这句的时候在普通查找树中是会判断x是否指向NULL,但在这里不用,因为就算x是哨兵nil,其父指针即使指向被删除的节点y的父亲;
3) 在最后即将调用eraseFixup的时候,判断y是否为黑色,若是,则调用eraseFixup;否则不用,此时红黑性质依然得以保持,原因如下:
a) 树中各节点的黑高度没有变化;
b) 不存在两个相邻的红色节点,否则删除调整前红黑性质就破坏了;
c) 因为y若是红色,就不可能是根,所以根依然是黑色。
传递给eraseFixup的节点x是以下两个节点中的一个:在y被删除前,如果y有个不是哨兵的孩子,则x是y唯一的孩子;若y没有孩子,则x是哨兵nil。下面我们来看看eraseFixup是如何保持红黑性质的:
eraseFixup(T, z)
{
while (x != root[T] && color[x] == black)
{
if (x == left[parent[x]])
{//x是其父亲左孩子
brother <- right[parent[x]];
if (color[brother] == red)
{//情况1,x兄弟节点为红色
color[brother] <- black;
color[parent[x]] <- red;
leftRotate(T, parent[x]);
brother <- right[parent[x]];
}
if (color[left[brother] == black && color[right[brother]]] == black)
{//情况2,x兄弟节点为黑色,且其两个孩子也是黑色
color[brother] <- red;
x <- parent[x];
}
else if (color[right[x]] == black)
{//情况3,x兄弟节点为黑色,但是左孩子为红色,右孩子为黑色
color[left[brother]] <- black;
color[brothe] <- red;
rightRotate(T, brother);
brother <- right[parent[x]];
}
//情况4,x兄弟节点为黑色,但是右孩子为红色
color[brother] <- color[parent[x]];
color[parent[x]] <- black;
color[right[brother]] <- black;
leftRotate(T, parent[x]);
x <- root[T];
}
else //x是其父亲右孩子,
//和第一个if语句对称,将其中的所有left和right换成right和left
}
color[x] <- black;
}首先,我们分析一下,删除过程可能会破坏哪些红黑性质,然后针对地提出解决方案。只有被删节点是黑色时才会调用该过程,可能会产生三个问题:
1) 如果y原来是根节点,而现在y的一个红孩子成为新根,那么违反了性质2;
2) 如果x和parent[y]都是红色,那么就会破坏性质4;
3) 删除了y之后导致先前包含y的任何路径上的黑节点个数减少1,违反性质5。对于这个违反有一个简单的解决方案就是将父节点,也就是y,的那重黑色“下放”给x,那么性质5得以保持。这样会带来另一个问题,那就是如果x是原本为黑,那么现在就是双黑;若原本为红,那么现在就是红黑,当然,x的color属性依然是红(若x为红黑)或者黑(若x为双黑),换句话说,也就是x指向谁,谁就还有另外一重黑色,而不管它原本是什么颜色,那么这个就违反了性质1。
过程eraseFixup就是来恢复上述性质1、2、4的,我们着力分析性质1的恢复,其他两者在恢复性质1的过程中都可以“顺带”被恢复。如何恢复性质1呢?我们定性的把这个过程称之为“甩黑锅”,注意:”甩“这个动作在整个算法中体现的是,x指向谁,谁就背了这重黑锅。
我们可以理解整个过程:x的父亲被删了,但是它的黑锅还是要留下的(因为要保持性质5),那么就只有把这个黑锅甩给它儿子x,毕竟父债子还;但是x扛不起两个黑锅,那么它就要想方设法找其他红节点,把这个黑锅甩给它,到这里,红节点,记为w,就背了这重黑锅,那么w就是红黑两色了,任务就落到了它的身上,它开始继续这个过程。该过程是自下而上的,且发生在包含y的那些路径上。
a) 甩给了根,即while循环第一个条件不满足,很简单,将其直接置为黑,问题解决。有人会问,如果此时根是黑色呢,那么它岂不是背了两个黑锅?是的,但是这个已经不重要了,因为红黑性质得到了保持,只是整棵树的黑高度降低了1;
b) 甩给了某个红节点,即while循环第二个条件不满足,那么直接置为黑色,让它专注于背黑锅三十年;
c) 甩给了某黑节点且该节点不是根,即满足while循环条件,那么它任重而道远,必须继续进入循环体,继续甩黑锅之路了,最终问题会转化为a) 或b)。因而,在整个while循环体中,x永远指向具有双黑的非根节点上。
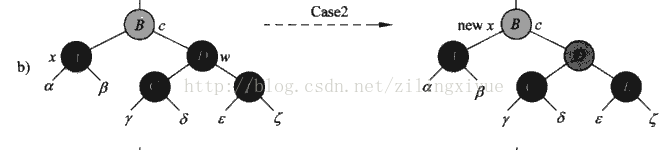
对于情况c) 是最复杂的,因为循环体险恶异常,总共包含了以下四种情况,严格来说是八种,但是由于左右子树对称,只要分析其中四种就好了,我们以x是其父节点的左孩子为例:
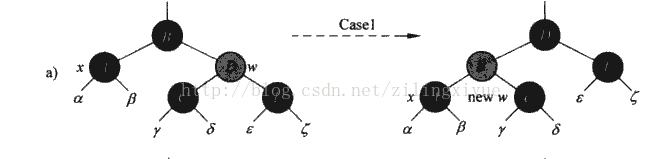
情况1:x的兄弟w是红色的
图解
伪代码:
if (color[brother] == red)
{//情况1,x兄弟节点为红色
color[brother] <-black;
color[parent[x]] <-red;
leftRotate(T, parent[x]);
brother <-right[parent[x]];
}
目的:将情况1转换为情况2,3或者4。
情况2:x的兄弟节点是黑色的,且两个孩子也是黑色的
图解:
伪代码:
if (color[left[brother] == black && color[right[brother]]] == black)
{//情况2,x兄弟节点为黑色,且其两个孩子也是黑色
color[brother] <-red;
x <-parent[x];
}
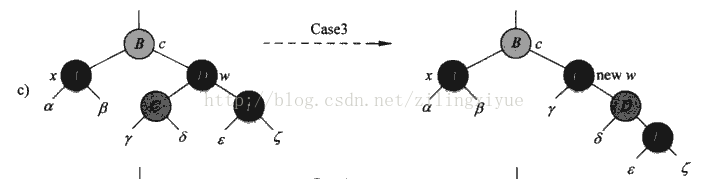
情况3:x的兄弟节点是黑色的额,但是其左孩子红,右孩子黑;
图解:
伪代码:
else if (color[right[x]] == black)
{//情况3,x兄弟节点为黑色,但是左孩子为红色,右孩子为黑色
color[left[brother]] <-black;
color[brothe] <-red;
rightRotate(T, brother);
brother <-right[parent[x]];
}
目的:将情况3转变为情况4.
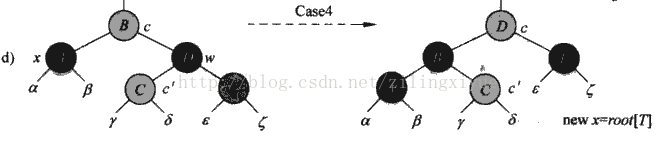
情况4:x的兄弟节点是黑色的,但是其右孩子为红。
图解:
伪代码:
//情况4,x兄弟节点为黑色,但是右孩子为红色
color[brother] <- color[parent[x]];
color[parent[x]] <- black;
color[right[brother]] <- black;
leftRotate(T, parent[x]);
x <- root[T];
结果:测试while循环条件是满足,不满足即将结束,否则继续入坑。
与普通的二叉查找树相比较,整个红黑树的操作中大多数操作极其类似,只有删除和插入后的调整不同,而且这也正是红黑树最复杂的地方。对此,我肯定有理解不到位的地方,还请各位coder指出。
下面是我所写的红黑树的C++代码:
#include<iostream>
using namespace std;
enum COLOR { red, black };//枚举,定义颜色
template <typename T> class RBTree;
template <typename T>
class node
{
private:
friend class RBTree<T>;
node *parent;
node *left;
node *right;
T key;
COLOR color;
node(){}//默认构造函数,只供创建nil时调用
public:
node(const T &k, COLOR c = red) :key(k), color(c),
parent(NULL), left(NULL), right(NULL){}
T& getKey(){ return key; }
const T& getKey()const { return key; }
//省略指针域的getter和setter
};
template <typename T>
class RBTree
{
private:
static node<T> *nil;//哨兵,静态成员,被整个RBTree类所共有
node<T> *root;
RBTree(const RBTree&);//禁止复制构造
RBTree operator=(const RBTree&);//禁止赋值
void leftRotate(node<T>*);//左旋
void rightRotate(node<T>*);//右旋
void insertFixup(node<T>*);//插入节点后红黑性质调整
void eraseFixup(node<T>*);//删除节点后红黑性质调整
public:
RBTree() :root(nil)
{
root->parent = nil;
root->left = nil;
root->right = nil;
root->color = black;
}
RBTree(node<T> *rbt) :root(rbt){}//复制构造函数,用于创建子红黑树对象
void insert(const T&);//插入
void create();//创建红黑树
void erase(const T&);//删除
node<T>* locate(const T&)const;//查找
node<T>* minMum()const;//最小值
node<T>* maxMum()const;//最大值
node<T>* successor(const T&)const;//找后继
node<T>* predecessor(const T&)const;//前驱
void preTraversal()const;//先根遍历
void inTraversal()const;//中根遍历
void destroy();//销毁红黑树
bool empty()const{ return root == nil; }//判空
};
template <typename T> node<T> *RBTree<T>::nil = new node<T>;//定义静态成员nil
template <typename T>
void RBTree<T>::leftRotate(node<T> *curr)
{
if (curr->right != nil)
{//存在右孩子时才能左旋
node<T> *rchild = curr->right;
curr->right = rchild->left;
if (rchild->left != nil)
rchild->left->parent = curr;
rchild->parent = curr->parent;
if (curr->parent == nil)
root = rchild;
else if (curr == curr->parent->left)
curr->parent->left = rchild;
else curr->parent->right = rchild;
curr->parent = rchild;
rchild->left = curr;
}
}
template <typename T>
void RBTree<T>::rightRotate(node<T> *curr)
{
if (curr->left != nil)
{//存在左孩子时才能右旋
node<T> *lchild = curr->left;
curr->left = lchild->right;
if (lchild->right != nil)
lchild->right->parent = curr;
lchild->parent = curr->parent;
if (curr->parent == nil)
root = lchild;
else if (curr == curr->parent->left)
curr->parent->left = lchild;
else curr->parent->right = lchild;
lchild->right = curr;
curr->parent = lchild;
}
}
template <typename T>
void RBTree<T>::insert(const T &k)
{
node<T> *pkey = new node<T>(k),
*p = nil, *curr = root;
while (curr != nil)
{//找插入位置
p = curr;//记住当前节点父亲
if (k < curr->key)//往左找
curr = curr->left;
else curr = curr->right;//向右找
}
pkey->parent = p;
if (p == nil)//插入的是第一个节点
root = pkey;
else if (k < p->key)
p->left = pkey;
else p->right = pkey;
pkey->left = pkey->right = nil;
insertFixup(pkey);//调整
}
template <typename T>
void RBTree<T>::insertFixup(node<T> *curr)
{
while (curr->parent->color == red)
{//父亲为红节点时才需要进入循环调整
if (curr->parent == curr->parent->parent->left)
{//父亲是祖父左孩子
node<T> *uncle = curr->parent->parent->right;
if (uncle != nil && uncle->color == red)
{//情况1,叔叔节点存在且为红色
curr->parent->color = black;
uncle->color = black;
curr->parent->parent->color = red;
curr = curr->parent->parent;
}
else if (curr == curr->parent->right)
{//情况2,叔叔节点为黑色,且当前节点是父亲右孩子
curr = curr->parent;
leftRotate(curr);//将父节点左旋,以转变为情况3
}
else
{//情况3,叔叔节点为黑色,且当前节点是父亲左孩子
curr->parent->color = black;
curr->parent->parent->color = red;
rightRotate(curr->parent->parent);
}
}
else
{//父亲是祖父右孩子,与上面三种情况对称
node<T> *uncle = curr->parent->parent->left;
if (uncle != nil && uncle->color == red)
{//情况1
curr->parent->color = black;
uncle->color = black;
curr->parent->parent->color = red;
curr = curr->parent->parent;
}
else if (curr == curr->parent->left)
{//情况2
curr = curr->parent;
rightRotate(curr);
}
else
{//情况3
curr->parent->color = black;
curr->parent->parent->color = red;
leftRotate(curr->parent->parent);
}
}
}
root->color = black;//跳出循环时将根节点置为黑色
}
template <typename T>
void RBTree<T>::create()
{
T k;
cout << "Enter element(s),CTRL+Z to end" << endl;//换行后CTRL+Z结束输入
while (cin >> k)
insert(k);
cin.clear();
}
template <typename T>
void RBTree<T>::preTraversal()const
{
node<T> *curr = root;
if (curr != nil)
{
cout << curr->key << " : ";
if (curr->color == red) cout << "red" << endl;
else cout << "black" << endl;
RBTree LEFT(curr->left);//继续左子树先根遍历
LEFT.preTraversal();
RBTree RIGHT(curr->right);
RIGHT.preTraversal();
}
}
template <typename T>
void RBTree<T>::inTraversal()const
{
node<T> *curr = root;
if (curr != nil)
{
RBTree LEFT(curr->left);
LEFT.inTraversal();
cout << curr->key << " : ";
if (curr->color == red) cout << "red" << endl;
else cout << "black" << endl;
RBTree RIGHT(curr->right);//继续右子树中根遍历
RIGHT.inTraversal();
}
}
template <typename T>
node<T>* RBTree<T>::successor(const T &k)const
{
node<T> *curr = locate(k);
if (curr->right != nil)
{//若右子树不为空,则后继为右子树最小值
RBTree RIGHT(curr->right);
return RIGHT.minMum();
}
node<T> *p = curr->parent;
while (p != nil && curr == p->right)
{//否则为沿右指针一直向上直到第一个拐弯处节点
curr = p;
p = p->parent;
}
return p;
}
template <typename T>
node<T>* RBTree<T>::minMum()const
{
node<T> *curr = root;
while (curr->left != nil)
curr = curr->left;
return curr;
}
template <typename T>
node<T>* RBTree<T>::maxMum()const
{
node<T> *curr = root;
while (curr->right != nil)
curr = curr->right;
return curr;
}
template <typename T>
node<T>* RBTree<T>::predecessor(const T &k)const
{
node<T> *curr = locate(k);
if (curr->left != nil)
{//若左子树不为空,则前驱为左子树最大值
RBTree LEFT(curr->left);
return LEFT.maxMum();
}
node<T> *p = curr->parent;
while (p != nil && curr == p->left)
{//否则为沿左指针一直往上的第一个拐弯处节点
curr = p;
p = p->parent;
}
return p;
}
template <typename T>
void RBTree<T>::erase(const T &k)
{
node<T> *curr = locate(k), *pdel, *child;
if (curr->left == nil || curr->right == nil)//决定删除节点
pdel = curr;//若当前节点至多有一个孩子,则删除它
else pdel = successor(k);//否则若有两孩子,则删除其后继
if (pdel->left != nil)//记下不为空的孩子
child = pdel->left;
else child = pdel->right;
child->parent = pdel->parent;
if (pdel->parent == nil)//若删除的是根节点
root = child;
else if (pdel == pdel->parent->left)//否则若被删节点是其父亲左孩子
pdel->parent->left = child;
else pdel->parent->right = child;
if (curr != pdel)
curr->key = pdel->key;//若被删的是后继,则将后继值赋给当前节点
if (pdel->color == black)//被删节点为黑色时才调整
eraseFixup(child);
delete pdel;//释放所占内存
}
template <typename T>
void RBTree<T>::eraseFixup(node<T> *curr)
{
while (curr != root && curr->color == black)
{//当前不为根,且为黑色
if (curr == curr->parent->left)
{//若其是父亲左孩子
node<T> *brother = curr->parent->right;//兄弟节点肯定存在
if (brother->color == red)
{//情况1,兄弟是红色,转变为情况2,3,4
brother->color = black;
curr->parent->color = red;
leftRotate(curr->parent);
brother = curr->parent->right;
}
if (brother->left->color == black && brother->right->color == black)
{//情况2,兄弟是黑色,且两孩子也是黑色,将当前节点和兄弟去一重黑色
brother->color = red;
curr = curr->parent;
}
else if (brother->right->color == black)
{//情况3,兄弟左孩子为红,右孩子为黑,转变为情况4
brother->color = red;
brother->left->color = black;
rightRotate(brother);
brother = curr->parent->right;
}
else
{//情况4,右孩子为黑色,左孩子随意
brother->color = curr->parent->color;
curr->parent->color = black;
brother->right->color = black;
leftRotate(curr->parent);
curr = root;
}
}
else
{//若其是父亲右孩子,与上面四中情况对称
node<T> *brother = curr->parent->left;
if (brother->color == red)
{//情况1
brother->color = black;
curr->parent->color = red;
rightRotate(curr->parent);
brother = curr->parent->left;
}
if (brother->right->color == black && brother->left->color == black)
{//情况2
brother->color = red;
curr = curr->parent;
}
else if (brother->left->color == black)
{//情况3
brother->color = red;
brother->right->color = black;
leftRotate(brother);
brother = curr->parent->left;
}
else
{//情况4
brother->color = curr->parent->color;
curr->parent->color = black;
brother->left->color = black;
rightRotate(curr->parent);
curr = root;
}
}
}
curr->color = black;//结束循环时将当前节点置为黑色
}
template <typename T>
node<T>* RBTree<T>::locate(const T &k)const
{
node<T> *curr = root;
while (curr != nil && curr->key != k)
{
if (k < curr->key)curr = curr->left;
else curr = curr->right;
}
return curr;
}
template <typename T>
void RBTree<T>::destroy()
{
while (root != nil)
{
cout << "erase: " << root->key << endl;
erase(root->key);
}
delete nil;
}
int main()
{//12 5 18 2 9 15 19 17
RBTree<int> rbt;
cout << "-------------create------------" << endl;
rbt.create();
cout << "------------inTraversal--------" << endl;
rbt.inTraversal();
rbt.insert(10);
rbt.insert(-12);
rbt.insert(100);
cout << "---after insert inTraversal----" << endl;
rbt.inTraversal();
cout << "--------------min_max----------" << endl;
cout << "max: " << rbt.maxMum()->getKey() << endl;
cout << "min: " << rbt.minMum()->getKey() << endl;
cout << "--------------suc_prede----------" << endl;
cout << "12_suc: " << rbt.successor(12)->getKey() << endl;
cout << "12_prede: " << rbt.predecessor(12)->getKey() << endl;
cout << "------------preTraversal-------" << endl;
rbt.preTraversal();
cout << "--------------locate-----------" << endl;
cout << "17_locate: " << rbt.locate(17)->getKey() << endl;
rbt.erase(100);
cout << "---after erase inTraversal----" << endl;
rbt.inTraversal();
cout << "------------destroy-----------" << endl;
rbt.destroy();
getchar();
return 0;
}









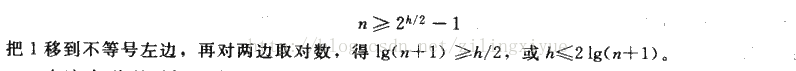














 441
441











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








