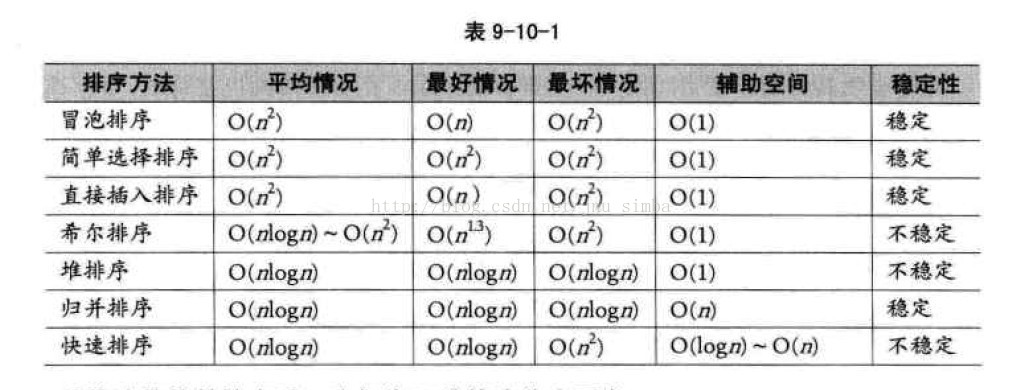
排序算法效率比较
各种排序算法的比较
冒泡排序
基本定义
两两比较相邻记录的的关键字,如果反序则交换,直到没有反序的记录为止。
时间复杂度分析
最好的情况是,数组是有序的,只需要n - 1次的比较,时间复杂度是
O(n)
最坏的情况是,数组是逆序的,需要比较
代码实现
void Bubble_sort(int arr[], int len)
{
bool flag = true;
for(int i = 0; i < len && flag; i ++)
{
flag = false;
for(int j = len - 1; j > i; j --)
{
if(arr[j-1] > arr[j])
{
flag = true;
swap(arr[j-1], arr[j]);
}
}
}
}选择排序
基本定义
首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
时间复杂度分析
比较次数 O(n2) ,比较次数与关键字的初始状态无关,总的比较次数
代码实现
void Select_sort(int arr[], int len)
{
int min_index;
for(int i = 0; i < len; i ++)
{
min_index = i;
for(int j = i+1; j < len; j++)
{
if(arr[j] < arr[min_index])
min_index = j;
}
if(i != min_index)
swap(arr[min_index], arr[i]);
}
}插入排序
基本定义
它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。

时间复杂度分析
最好情况就是,序列已经是升序排列了,在这种情况下,需要进行的比较操作需 (n−1) 次即可。
最坏情况就是,序列是降序排列,那么此时需要进行的比较共有 n(n−1)/2 次。插入排序的赋值操作是比较操作的次数减去 (n−1) 次。平均来说插入排序算法复杂度为 O(n2) 。
代码实现
void Insert_Sort(int arr[], int len)
{
int key;
int i, j;
for(i = 1; i < len; i ++)
{
key = arr[i];
for(j = i; j > 0; j --)
{
if(arr[j-1] < key)
break;
arr[j] = arr[j-1];
}
arr[j] = key;
}
}希尔排序
基本定义
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。

时间复杂度分析
希尔排序的时间复杂度跟选取步长序列有关,步长序列如果是 n/2i 的话,最坏的情况下的复杂度为 O(n2) ,步长序列如果是 (3k–1)/2 的话,最坏的情况下的复杂度为 O(n3/2) 。
代码实现
void Shell_Sort(int arr[], int len)
{
int increment = 0;
int key;
int i,j;
for(increment = len / 2; increment > 0; increment /= 2)
{
for(i = increment; i < len; i ++)
{
key = arr[i];
for(j = i; j >=increment; j -=increment)
{
if(arr[j-increment] < key)
break;
arr[j] = arr[j-increment];
}
arr[j] = key;
}
}
}归并排序
基本定义
归并排序(Merge Sort)完全遵循上述分治法三个步骤:
1、分解:将要排序的n个元素的序列分解成两个具有n/2个元素的子序列;
2、解决:使用归并排序分别递归地排序两个子序列;
3、合并:合并两个已排序的子序列,产生原问题的解。
所以说归并排序一种分治算法的典型应用。

时间复杂度分析
时间复杂度是 O(nlogn) ,空间复制度为 O(n) (归并排序的最大缺陷)。归并排序在数据量比较大的时候也有较为出色的表现(效率上),但是,其空间复杂度 O(n) 使得在数据量特别大的时候(例如,1千万数据)几乎不可接受。而且,考虑到有的机器内存本身就比较小。总结来说,归并排序是一种占用内存,但却效率高且稳定的算法。
代码实现
void merge_array(int arr[], int tmp[], int left, int mid, int right)
{
int i = left;
int j = mid + 1;
int index = 0;
while(i <= mid && j <= right)
{
if(arr[i] < arr[j])
tmp[index++] = arr[i++];
else
tmp[index++] = arr[j++];
}
while(i <= mid)
tmp[index++] = arr[i++];
while(j <= right)
tmp[index++] = arr[j++];
memcpy(arr + left, tmp, (right - left + 1) * sizeof(int));
}
void mergesort(int arr[], int tmp[], int left, int right)
{
int mid;
if(left < right)
{
mid = (left + right) / 2;
mergesort(arr, tmp, left, mid);
mergesort(arr, tmp, mid + 1, right);
merge_array(arr, tmp, left, mid, right);
}
}
void Merge_Sort(int arr[], int len)
{
assert(arr && len);
int *tmp = new int[len];
mergesort(arr, tmp, 0, len - 1);
delete[] tmp;
}堆排序
基本定义
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。堆排序可以看作是对选择排序的改进。
通常堆是通过一维数组来实现的。在起始数组为0的情形中:
- 父节点i的左子节点在位置 (2∗i+1) ;
- 父节点i的右子节点在位置 (2∗i+2) ;
- 子节点i的父节点在位置 floor((i−1)/2) ;
在堆的数据结构中,堆中的最大值总是位于根节点。堆中定义以下几种操作:
- 最大堆调整(Max_Heapify):将堆的末端子节点作调整,使得子节点永远小于父节点
- 创建最大堆(Build_Max_Heap):将堆所有数据重新排序
- 堆排序(HeapSort):移除位在第一个数据的根节点,并做最大堆调整的递归运算
时间复杂度分析
建立N个元素的二叉堆需要花费
O(n)
,在正式排序时,第
i
次取堆顶的数据事,重建堆需要用
代码实现
void Heap_adjust(int arr[], int index, int len)
{
int iMax = index;
int iLeftChild = 2 * index + 1;
int iRightChild = 2 * index + 2;
if(iLeftChild < len && arr[index] < arr[iLeftChild])
iMax = iLeftChild;
if(iRightChild < len && arr[iMax] < arr[iRightChild])
iMax = iRightChild;
if(iMax != index)
{
swap(arr[iMax], arr[index]);
Heap_adjust(arr, iMax, len);
}
}
void Build_Maxheap(int arr[], int len)
{
for(int i = len / 2; i >= 0; i--)
{
Heap_adjust(arr, i, len);
}
}
void Heap_Sort(int arr[], int len)
{
Build_Maxheap(arr, len);
for(int i = len - 1; i > 0; i --)
{
swap(arr[0], arr[i]);
Heap_adjust(arr, 0 , i);
}
}快速排序
基本定义
快速排序使用分治法(Divide and conquer)策略来把一个序列(list)分为两个子序列(sub-lists)。
算法步骤
算法步骤简述如下:
- 选择一个基准值(pivot)(选择方法很多,可以固体选某个值,比如第一个或最后一个或中间值,或者是三数取中法等);
- 将比基准值(pivot)小的数值划分到基准值左边,构成左子串列,将比基准值(pivot)大的数值划分到基准值右边,构成右子串列;
- 分别对左子串列和右子串列递归地作上述两个步骤;
- 直到左子串列或右子串列只剩一个值或者为空。
基准值的选取
上面的第一步基准值的选择对快速排序的效率有很大关系。基准值(pivot)的选择办法有下面几种:
- 固定位置:第一个,最后一个或中间值;
- 随机选取:用随机函数随机选取一个;
- 三数取中:去第一个,中间值和最后一个数的平均值。
固定位置和随机选取的方法容易造成一种极端,如果选取的那个数刚好是最小值或最大值,比如数组是有序的,就会导致一个很差的分割,是左子串或右子串列为0,而且随机选取过程还会有额外的时间开销。所以都是不可取的。三数取中的办法就避免了上面的情况。
时间复杂度分析
快速排序的时间性能跟递归的深度有关,而空间复杂度跟递归造成的栈空间使用有关。最好的情况是,选取的基准值刚好是中位数,刚好将数据等分成2个子串,递归树也就是平衡的。递归调用需要 log2n 次,空间复杂度为 O(logn) ,时间复杂度为 O(nlogn) ;最坏的情况就是待排序的数据是有序的,正序或者逆序。递归需要 n−1 次,空间复杂度则需要 O(n) 时间复杂度为 O(n2)
代码实现
int Partition(int arr[], int iLeft, int iRigth)
{
int mid = iLeft + (iRigth - iLeft) / 2;
if(arr[iLeft] > arr[iRigth])
swap(arr[iLeft], arr[iRigth]);
if(arr[mid] > arr[iRigth])
swap(arr[iRigth], arr[mid]);
if(arr[mid] > arr[iLeft])
swap(arr[mid], arr[iLeft]);
int pivot_key = arr[iLeft];
while(iLeft < iRigth)
{
while(iLeft < iRigth && arr[iRigth] >= pivot_key)
iRigth --;
arr[iLeft] = arr[iRigth];
while(iLeft < iRigth && arr[iLeft] <= pivot_key)
iLeft ++;
arr[iRigth] = arr[iLeft];
}
arr[iLeft] = pivot_key;
return iLeft;
}
void qsort(int arr[], int iLeft, int iRigth)
{
if(iLeft < iRigth)
{
int pivot_index = Partition(arr, iLeft, iRigth);
qsort(arr, iLeft, pivot_index - 1);
qsort(arr, pivot_index + 1, iRigth);
}
}
void Qsort(int arr[], int len)
{
qsort(arr, 0, len - 1);
}测试程序
#include <iostream>
#include <cstring>
#include <ctime>
#include <stdlib.h>
#include <assert.h>
#include <cmath>
using namespace std;
#define ArraySize 10
void swap(int *x, int *y)
{
int temp;
temp = *x;
*x = *y;
*y = temp;
}
void Print_array(int arr[], int len)
{
for(int i = 0; i < len; i++)
{
cout << arr[i] << " ";
}
cout << endl;
}
void Bubble_sort(int arr[], int len)
{
bool flag = true;
for(int i = 0; i < len && flag; i ++)
{
flag = false;
for(int j = len - 1; j > i; j --)
{
if(arr[j-1] > arr[j])
{
flag = true;
swap(arr[j-1], arr[j]);
}
}
}
}
void Slect_sort(int arr[], int len)
{
int min_index;
for(int i = 0; i < len; i ++)
{
min_index = i;
for(int j = i+1; j < len; j++)
{
if(arr[j] < arr[min_index])
min_index = j;
}
if(i != min_index)
swap(arr[min_index], arr[i]);
}
}
void Insert_Sort(int arr[], int len)
{
int key;
int i, j;
for(i = 1; i < len; i ++)
{
key = arr[i];
for(j = i; j > 0; j --)
{
if(arr[j] < key)
break;
arr[j] = arr[j-1];
}
arr[j] = key;
}
}
void Shell_Sort(int arr[], int len)
{
int increment = 0;
int key;
int i,j;
for(increment = len / 2; increment > 0; increment /= 2)
{
for(i = increment; i < len; i ++)
{
key = arr[i];
for(j = i; j >=increment; j -=increment)
{
if(arr[j-increment] < key)
break;
arr[j] = arr[j-increment];
}
arr[j] = key;
}
}
}
void merge_array(int arr[], int tmp[], int left, int mid, int right)
{
int i = left;
int j = mid + 1;
int index = 0;
while(i <= mid && j <= right)
{
if(arr[i] < arr[j])
tmp[index++] = arr[i++];
else
tmp[index++] = arr[j++];
}
while(i <= mid)
tmp[index++] = arr[i++];
while(j <= right)
tmp[index++] = arr[j++];
memcpy(arr + left, tmp, (right - left + 1) * sizeof(int));
}
void mergesort(int arr[], int tmp[], int left, int right)
{
int mid;
if(left < right)
{
mid = (left + right) / 2;
mergesort(arr, tmp, left, mid);
mergesort(arr, tmp, mid + 1, right);
merge_array(arr, tmp, left, mid, right);
}
}
void Merge_Sort(int arr[], int len)
{
assert(arr && len);
int *tmp = new int[len];
mergesort(arr, tmp, 0, len - 1);
delete[] tmp;
}
void Heap_adjust(int arr[], int index, int len)
{
int iMax = index;
int iLeftChild = 2 * index + 1;
int iRightChild = 2 * index + 2;
if(iLeftChild < len && arr[index] < arr[iLeftChild])
iMax = iLeftChild;
if(iRightChild < len && arr[iMax] < arr[iRightChild])
iMax = iRightChild;
if(iMax != index)
{
swap(arr[iMax], arr[index]);
Heap_adjust(arr, iMax, len);
}
}
void Build_Maxheap(int arr[], int len)
{
for(int i = len / 2; i >= 0; i--)
{
Heap_adjust(arr, i, len);
}
}
void Heap_Sort(int arr[], int len)
{
Build_Maxheap(arr, len);
for(int i = len - 1; i > 0; i --)
{
swap(arr[0], arr[i]);
Heap_adjust(arr, 0 , i);
}
}
int Partition(int arr[], int iLeft, int iRigth)
{
int mid = iLeft + (iRigth - iLeft) / 2;
if(arr[iLeft] > arr[iRigth])
swap(arr[iLeft], arr[iRigth]);
if(arr[mid] > arr[iRigth])
swap(arr[iRigth], arr[mid]);
if(arr[mid] > arr[iLeft])
swap(arr[mid], arr[iLeft]);
int pivot_key = arr[iLeft];
while(iLeft < iRigth)
{
while(iLeft < iRigth && arr[iRigth] >= pivot_key)
iRigth --;
arr[iLeft] = arr[iRigth];
while(iLeft < iRigth && arr[iLeft] <= pivot_key)
iLeft ++;
arr[iRigth] = arr[iLeft];
}
arr[iLeft] = pivot_key;
return iLeft;
}
void qsort(int arr[], int iLeft, int iRigth)
{
if(iLeft < iRigth)
{
int pivot_index = Partition(arr, iLeft, iRigth);
qsort(arr, iLeft, pivot_index - 1);
qsort(arr, pivot_index + 1, iRigth);
}
}
void Qsort(int arr[], int len)
{
qsort(arr, 0, len - 1);
}
int main(int argc, char const *argv[])
{
/* code */
int Array[ArraySize];
srand(time(NULL));
for(int i = 0; i < ArraySize; i ++)
{
Array[i] = rand()%100;
//cout << Array[i] << " ";
}
Print_array(Array, ArraySize);
Qsort(Array, ArraySize);
Print_array(Array, ArraySize);
return 0;
}





















 1210
1210

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








