兄弟们大家好,本来说好的是星期五出连连看的。不过被我给睡过去了,这些天一直都很瞌睡。不过睡眠好了做事的效率就高。希望兄弟们不要见怪。废话话不多说,首先我先说明说明一下《连连看地图布局之谜》
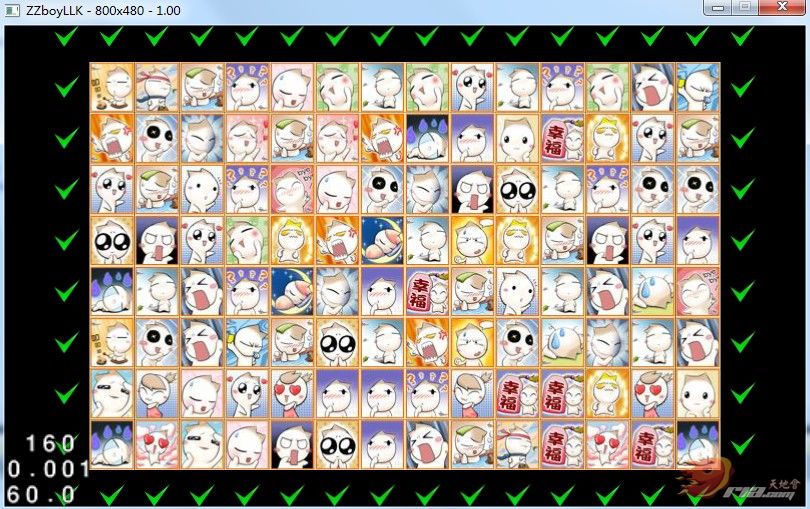
先上一张图给大家看看
当大家看到这张图片的时候会看到周围一圈对号,这个是我做标记用的,当然 真正的开发游戏过程中 这些对号是不存在的。我这里想给大家说明的是 假如我们的 地图是14*8的 那么其实真正的地图布局应该是16*10 为什么要这么做呢 那是因为我们要让我们所有的路线都从我们规定的方格内经过,不能越界。如果你是14*8 的那么当四边上有可以连通的时候 就要做大量的判断来处理。那么为什么我们不避免这些问题呢。这样我们在规划路线的时候 就不存在了特殊的情况。
不知道大家是否明白我说的什么意思。如果不懂的话可以给我留言我会给大家回复 解答。
关于图片的生成我这里说一下 如何保证所有的图片 都是成对出现呢 这里有个前提条件就是我们的地图布局一定要成偶数。那么我们在生出图片的 我们每一次取出一张图片生成两个一模一样的 这样就保证地图里面所有的图片肯定是成对出现的。
主要代码是这样的
int totalcout=this->row*this->cloum;
CCSpriteFrameCache::sharedSpriteFrameCache()->addSpriteFramesWithFile("point.plist","point.png");
CCArray* temparry=CCArray::create();
// 一次生成两张一样的
for (int i=0;i<totalcout/2;i++){
int num=CCRANDOM_0_1()*35;//因为是图片的张数是从0到36张 所以随机从0 到35
CustomSprite* phit1= CustomSprite::createWithSpritePicIndex(num,CCSize(picWidth,picHeight));
CustomSprite* phit2= CustomSprite::createWithSpritePicIndex(num,CCSize(picWidth,picHeight));
temparry->addObject(phit1);
temparry->addObject(phit2);
}是不是很简单啊
至于如何把生成的东西给打乱。这个cocos2d-x 提供了很好用的方法那就是从数组中取出的时候 可以随机去取出。
下面把整个地图布局的方法给贴出来
bool LLKmapLayer::setUpdateView(){
bool isRet=false;
do {
//得到需要的总张数 // 一定要是偶数
int totalcout=this->row*this->cloum;
CCSpriteFrameCache::sharedSpriteFrameCache()->addSpriteFramesWithFile("point.plist","point.png");
CCArray* temparry=CCArray::create();
// 一次生成两张一样的
for (int i=0;i<totalcout/2;i++){
int num=CCRANDOM_0_1()*35;//因为是图片的张数是从0到36张 所以随机从0 到35
CustomSprite* phit1= CustomSprite::createWithSpritePicIndex(num,CCSize(picWidth,picHeight));
CustomSprite* phit2= CustomSprite::createWithSpritePicIndex(num,CCSize(picWidth,picHeight));
temparry->addObject(phit1);
temparry->addObject(phit2);
}
for(int i=0;i<row+2;i++){
for(int j=0;j<this->cloum+2;j++){
if ((i==0)||(j==0)||(j==cloum+1)||(i==row+1)){
CustomSprite* temp= CustomSprite::createWithSpritePicIndex(0,CCSize(picWidth,picHeight));
temp->displayCustome();
temp->setX(j);
temp->setY(i);
temp->setAnchorPoint(ccp(0,0));
temp->setPosition(ccp(45*(j-1),51*(i-1)));
this->addChild(temp);
this->totalArray->addObject(temp);
}else {
CustomSprite* phit=(CustomSprite*)temparry->randomObject();
temparry->removeObject(phit,false);
phit->setAnchorPoint(ccp(0,0));
phit->setPosition(ccp(45*(j-1),51*(i-1)));
this->addChild(phit);
llkArray->addObject(phit);
phit->setX(j);
phit->setY(i);
this->totalArray->addObject(phit);
}
}
}
isRet=true;
} while (0);
return isRet;
}是不是很少的代码就实现了这个功能了。
下面就开始我们今天的重头戏 那就是连连看的主要算法
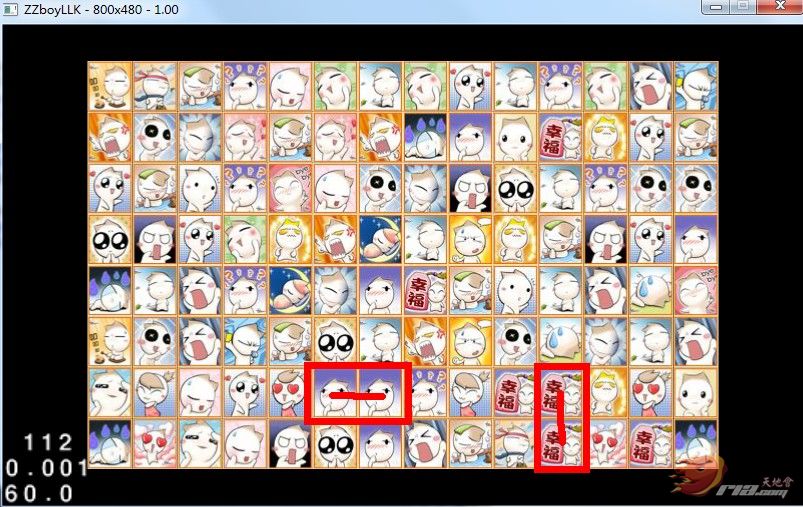
首先先说明最简单 那就是一线贯通。
大家看到我画的红线 是连连看中最简单的 两种连接方式
只要两张图片 处于同一水平线或者同一垂直线 如果两张图片中没有别的图片间隔就代表可以连通消除了
主要代码
// 这个是横向检测
CCArray* LLKAlgorithm::horizon(cocos2d::CCArray* llkArray,cocos2d::CCArray* hitArray){
CustomSprite* hit1=(CustomSprite*)hitArray->objectAtIndex(0);// 取出第一个
CustomSprite* hit2=(CustomSprite*)hitArray->objectAtIndex(1);// 取出第二个
int x1=hit1->getX(); // 得到第一个X 坐标
int x2=hit2->getX(); // 得到第二个X 坐标
bool isda=x1>x2?true:false;// 得出那个坐标肯后
int temp=isda?x1-x2:x2-x1; // 获取两个两个点之间的 间隔
CCArray* temparray=CCArray::create();// 记录两个点之间 所经过的点
if (temp==1){// 表示两个是相邻的两个
temparray->addObject(hit1);
temparray->addObject(hit2);
}else {
if (isda){
temparray->addObject(hit1);
temparray->addObject(hit2);
for(int i=1;i<temp;i++){
CustomSprite* hitteim=LLKAlgorithm::getCustByXandY(llkArray,x1-i,hit2->getY());
// 如果是已经消除的那么 就可以继续查询
if (!hitteim->getIsEliminate()){
LLKAlgorithm::removeAllArray(temparray,false);
break;
}else {
temparray->addObject(hitteim);
}
}
}else {
temparray->addObject(hit2);
temparray->addObject(hit1);
for(int i=1;i<temp;i++){
CustomSprite* hitteim=LLKAlgorithm::getCustByXandY(llkArray,x2-i,hit2->getY());
// 如果是已经消除的那么 就可以继续查询
if (!hitteim->getIsEliminate()){
LLKAlgorithm::removeAllArray(temparray,false);
break;
}else {
temparray->addObject(hitteim);
}
}
}
}
return temparray;
}
//这个是纵向检测
CCArray* LLKAlgorithm::vertical(cocos2d::CCArray* llkArray,cocos2d::CCArray* hitArray){
CustomSprite* hit1=(CustomSprite*)hitArray->objectAtIndex(0);// 取出第一个
CustomSprite* hit2=(CustomSprite*)hitArray->objectAtIndex(1);// 取出第二个
int y1=hit1->getY(); // 得到第一个Y 坐标
int y2=hit2->getY(); // 得到第二个Y 坐标
bool isda=y1>y2?true:false;// 得出那个坐标肯后
int temp=isda?y1-y2:y2-y1; // 获取两个两个点之间的 间隔
CCArray* temparray=CCArray::create();// 记录两个点之间 所经过的点
if (temp==1){// 表示两个是相邻的两个
temparray->addObject(hit1);
temparray->addObject(hit2);
}else {
if (isda){
temparray->addObject(hit1);
temparray->addObject(hit2);
for(int i=1;i<temp;i++){
CustomSprite* hitteim=LLKAlgorithm::getCustByXandY(llkArray,hit2->getX(),y1-i);
// 如果是已经消除的那么 就可以继续查询
if (!hitteim->getIsEliminate()){
LLKAlgorithm::removeAllArray(temparray,false);
break;
}else {
temparray->addObject(hitteim);
}
}
}else {
temparray->addObject(hit2);
temparray->addObject(hit1);
for(int i=1;i<temp;i++){
CustomSprite* hitteim=LLKAlgorithm::getCustByXandY(llkArray,hit2->getX(),y2-i);
// 如果是已经消除的那么 就可以继续查询
if (!hitteim->getIsEliminate()){
LLKAlgorithm::removeAllArray(temparray,false);
break;
}else {
temparray->addObject(hitteim);
}
}
}
}
return temparray;
}其中返回的 array 就是两个图片的之间的路径 包含两张图片在内。
对于两张图片是否可以垂直相连或者横向相连这个我不用多讲大家都应该明白怎么去做。
下面讲解一个拐角相连的情况
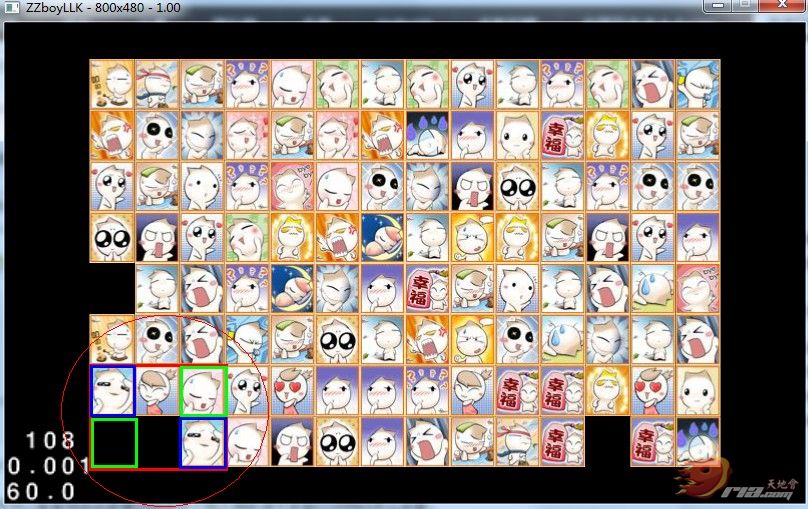
首先我先上张图
看到这张图片的时候大家先看蓝色矩形框里面 是两张可以经过一个拐角消除的图片 但是怎么确定两张图片可以经过一个拐角就可以连接呢
大家有没有发现 这两个张图片刚好是矩形的两个对角顶点 。也就是说围绕着两张图片我们可以画出一个最小的矩形,而矩形的其中两个顶点就是这两张图片。
好大家如果理解了这里 我们就说下面的,如果不理解好好的想一下。既然已知矩形的 其中两个顶点,那么另外两个顶点的坐标也就轻松的计算出来。就是我们看到的两个绿色的框。
我们先拿出最上面的那个绿色的矩形框,我们发现他不是一个空白或者说已经消除的一个图片 。那么这个顶点是不符合规则的。我们看下面的那个绿色矩形框。 我们惊奇的发现 他竟然和我们选择的那两张(蓝色框)图片能直接连通 也就是通过这个绿色的矩形框(已经消除掉的) 我们可以把他转化成 一个横向可以连通和一个纵向可以连通的。
看到这里有的人或许已经恍然大悟了。其实我们要向知道两个点是否可以经过一个拐角相连,我们首先要确定两个图片的坐标点是可以画出一个矩形的并且这个矩形的两个对角顶点就是你选中的两张图片。(必须是对角)然后我们找出这两个矩形另外两个顶点的坐标,找到时候首先要确定找到这个顶点必须是已经消除的掉的一个空白在哪里,或者说没有阻碍物。如果找到一个这样的顶点,那么只要这个顶点能和我们刚开始选择的那两张图片 形成一个纵向的连通和一个横向的连通 那么就说明这两个点可以经过一个拐角进行相连。
简单一点说就是 两个拐角的==想办法转成===》一个纵向连通+一个横向连通。
说到这里不知道大家是否已经明白我所表达的意思。
主要代码实现
CCArray* LLKAlgorithm::oneCorner(cocos2d::CCArray* llkArray,cocos2d::CCArray* hitArray){
CustomSprite* hit1=(CustomSprite*)hitArray->objectAtIndex(0);// 取出第一个
CustomSprite* hit2=(CustomSprite*)hitArray->objectAtIndex(1);// 取出第二个
int x1=hit1->getX();
int x2=hit2->getX();
int y1=hit1->getY();
int y2=hit2->getY();
bool isXg=x1>x2?true:false;//如果是true 表示hit1 在hit2 的后面
bool isYg=y1>y2?true:false;//如果是true 表示hit1 在hit2 的上面
// 下面我们计算出矩形的另外的两个重点
// 先计算出 在矩形上面所对应的
int temx=0;
int temy=0;
// 求取最上面的哪一个对应的坐标点
if(isYg){
temy=hit1->getY();
temx=hit2->getX();
}else {
temy=hit2->getY();
temx=hit1->getX();
}
CCArray* temparray=CCArray::create();// 记录两个点之间 所经过的点
CustomSprite* hity=LLKAlgorithm::getCustByXandY(llkArray,temx,temy);// 得到最上面的那个对应的矩形顶点的 精灵图片
CCArray* tempHit=CCArray::create();
//顶点必须是已经消除的 要不肯定不能贯通
if (hity->getIsEliminate()){
tempHit->addObject(hity);
tempHit->addObject(isYg?hit1:hit2);
CCArray* temx=LLKAlgorithm::horizon(llkArray,tempHit);// 获取X 方向上是否可以连通
if(temx->count()>0){// 表示可以连通
temparray->addObjectsFromArray(temx);
LLKAlgorithm::removeAllArray(tempHit,false);
tempHit->addObject(hity);
tempHit->addObject(isYg?hit2:hit1);
CCArray* temy=LLKAlgorithm::vertical(llkArray,tempHit);
if (temy->count()>0){
temparray->removeObject(hity,false);
temparray->addObjectsFromArray(temy);
}else {
LLKAlgorithm::removeAllArray(temparray,false);
}
}else {
LLKAlgorithm::removeAllArray(tempHit,false);
}
}
// 表示上面的路走不通
if (temparray->count()==0){
// 获取X 方向矩形所对应的的点
//temx=isXg?hit1->getX():hit2->getX();
//temy=isXg?hit2->getY():hit1->getY();
if (isYg){
temy=hit2->getY();
temx=hit1->getX();
}else {
temy=hit1->getY();
temx=hit2->getX();
}
CustomSprite* hitx=LLKAlgorithm::getCustByXandY(llkArray,temx,temy);// 得到最上面的那个对应的矩形顶点的 精灵图片
if (hitx->getIsEliminate()){
tempHit->addObject(hitx);
tempHit->addObject(isYg?hit2:hit1);
CCArray* temx=LLKAlgorithm::horizon(llkArray,tempHit);// 获取X 方向上是否可以连通
if(temx->count()>0){// 表示可以连通
temparray->addObjectsFromArray(temx);
LLKAlgorithm::removeAllArray(tempHit,false);
tempHit->addObject(hitx);
tempHit->addObject(isYg?hit1:hit2);
CCArray* temy=LLKAlgorithm::vertical(llkArray,tempHit);
if (temy->count()>0){
temparray->removeObject(hitx,false);
temparray->addObjectsFromArray(temy);
}else {
LLKAlgorithm::removeAllArray(temparray,false);
}
}else {
LLKAlgorithm::removeAllArray(tempHit,false);
}
}
}
return temparray;
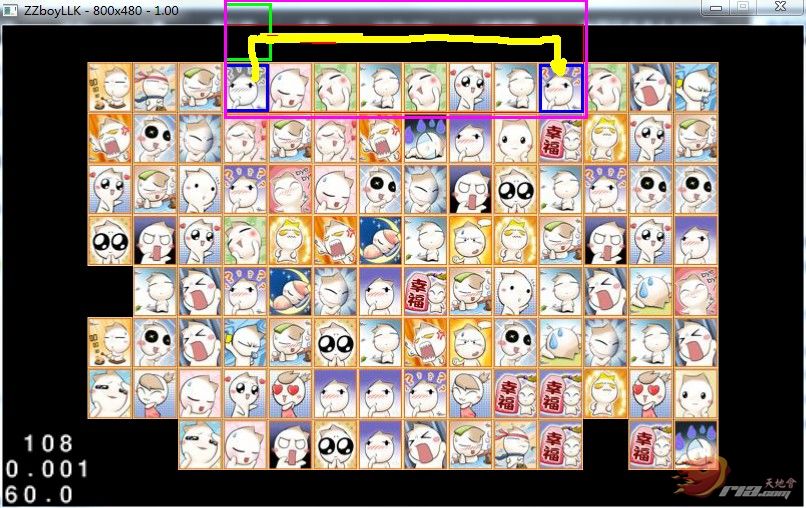
}下面我们说下拐两角 可以相连的。
大家看看蓝色区域内的是我选择的两张图片。从图中我们看出这两张图片是可以经过两个拐角相连的。
那么如何知道可以经过两个拐角可以 可以相连的 我相信通过上面那一个拐角的算法 大家或许就可以猜出来了。这里我详细说明一下 首先我们拿出一个点 那么就像这个点的上下左右去找,找到一个 可以经过一个拐角和另外一个点相连的。经过一个拐角的算法请看上面那个讲解。首先找到的这个点可以和我们拿出的这个点纵向相连或者横向相连 。(但是必须保证这个点已经没有别的图片占位置或者说是一个空白)。如果能找到这样的一个点那么就可以说明我们开始选择的两个图片是可以经过两个拐角进行相连的。
总体来说 可以这样理解 两个拐角==转化成===》(一个横向相连/纵向相连)+ 一个拐角可以相连的
一个拐角的看上面的解释。
主要实现代码
CCArray* LLKAlgorithm::twoCorner(cocos2d::CCArray* llkArray,cocos2d::CCArray* hitArray){
bool isjiance=false; // 这个主要来表示是否走了 一个拐角的判断
// 先获取 当前X 的最大是多少 y 的最大是多少
CustomSprite* lastCutom=(CustomSprite*)llkArray->lastObject();
int max=lastCutom->getX();
int may=lastCutom->getY();
CustomSprite* hit1=(CustomSprite*)hitArray->objectAtIndex(0);// 取出第一个
CustomSprite* hit2=(CustomSprite*)hitArray->objectAtIndex(1);// 取出第二个
// 随便拿出一个点 向他的四个方向出发 看看能否和另外一个变成一个拐角相连
// 这里我们就拿出取出的第一个点吧 hit1
CCArray* temparray=CCArray::create();// 记录两个点之间 所经过的点
int x1=hit1->getX(); // 得到第一个X 坐标
int y1=hit1->getY(); // 得到第1个Y坐标
// 首先向左检测
CCArray* temphit=CCArray::create();
temphit->addObject(hit2);
for(int i=(x1-1);i>=0;i--){
CustomSprite* tepcou =LLKAlgorithm::getCustByXandY(llkArray, i, y1);
if (tepcou->getIsEliminate()){
// 判断看能否组成一个矩形
temparray->addObject(tepcou);
if(tepcou->getX()==hit2->getX()||hit2->getY()==tepcou->getY()){
continue;
}
isjiance=true;
temphit->addObject(tepcou);
CCArray* temparr=LLKAlgorithm::oneCorner(llkArray,temphit);
if (temparr->count()>0){
temparray->addObjectsFromArray(temparr);
break;
}else {
if(i==0){
LLKAlgorithm::removeAllArray(temparray,false);
}
temphit->removeLastObject(false);
}
}else{
LLKAlgorithm::removeAllArray(temparray,false);
break;
}
}
if (isjiance==false){
LLKAlgorithm::removeAllArray(temparray,false);
}
if(temparray->count()==0){
bool isjiance=false;
// 向右检测
for(int i=(x1+1);i<=max;i++){
CustomSprite* tepcou =LLKAlgorithm::getCustByXandY(llkArray, i, y1);
if (tepcou->getIsEliminate()){
// 判断看能否组成一个矩形
temparray->addObject(tepcou);
if(tepcou->getX()==hit2->getX()||hit2->getY()==tepcou->getY()){
continue;
}
isjiance=true;
temphit->addObject(tepcou);
CCArray* temparr=LLKAlgorithm::oneCorner(llkArray,temphit);
if (temparr->count()>0){
temparray->addObjectsFromArray(temparr);
break;
}else {
if(i==max){
LLKAlgorithm::removeAllArray(temparray,false);
}
temphit->removeLastObject(false);
}
}else{
LLKAlgorithm::removeAllArray(temparray,false);
break;
}
}
if (isjiance==false){
LLKAlgorithm::removeAllArray(temparray,false);
}
}
if(temparray->count()==0){
bool isjiance=false;
// 向下检测
for(int i=(y1-1);i>=0;i--){
CustomSprite* tepcou =LLKAlgorithm::getCustByXandY(llkArray, x1, i);
if (tepcou->getIsEliminate()){
temparray->addObject(tepcou);
// 判断看能否组成一个矩形
if(tepcou->getX()==hit2->getX()||hit2->getY()==tepcou->getY()){
continue;
}
isjiance=true;
temphit->addObject(tepcou);
CCArray* temparr=LLKAlgorithm::oneCorner(llkArray,temphit);
if (temparr->count()>0){
temparray->addObjectsFromArray(temparr);
break;
}else {
if (i==0){
LLKAlgorithm::removeAllArray(temparray,false);
}
temphit->removeLastObject(false);
}
}else{
LLKAlgorithm::removeAllArray(temparray,false);
break;
}
}
if (isjiance==false){
LLKAlgorithm::removeAllArray(temparray,false);
}
}
if(temparray->count()==0){
bool isjiance=false;
// 向上检测
for(int i=(y1+1);i<=may;i++){
CustomSprite* tepcou =LLKAlgorithm::getCustByXandY(llkArray, x1, i);
if (tepcou->getIsEliminate()){
temparray->addObject(tepcou);
// 判断看能否组成一个矩形
if(tepcou->getX()==hit2->getX()||hit2->getY()==tepcou->getY()){
continue;
}
isjiance=true;
temphit->addObject(tepcou);
CCArray* temparr=LLKAlgorithm::oneCorner(llkArray,temphit);
if (temparr->count()>0){
temparray->addObjectsFromArray(temparr);
break;
}else {
if(i==may){
LLKAlgorithm::removeAllArray(temparray,false);
}
temphit->removeLastObject(false);
}
}else{
LLKAlgorithm::removeAllArray(temparray,false);
break;
}
}
if (isjiance==false){
LLKAlgorithm::removeAllArray(temparray,false);
}
}
if (temparray->count()>0){
temparray->addObject(hit1);
}
return temparray;写到这里连连看的算法基本算是已经完成了
我在网上看了很多方法感觉不太容易理解,这个是我自己想出来的。感觉很通俗易懂,其实就是化繁为简。我最麻烦的变成最简单。不过连连看的算法有很多种。不如著名的A* 寻路算法就可以。不过我感觉那个给大家讲解其实会很麻烦,有希望了解了解的同学可以在百度上上搜索一下A* 寻路算法。
其实我子所以写这个练练看看的算法是交大家以后学习中的一种思路,有些同学一开始把问题弄得很复杂导致一时半会想不通,我建议刚开始考虑情况的时候从最简单的开始考虑。到繁琐的阶段的时候看看能不能转化成 简单的方式。中国人其实都喜欢大事化小 小事化了 哈哈。 本章讲解结束。 至于重新布局+自动查找 等算法我会慢慢加进去 希望大家耐心等待。
另外给大家说下以后我所有的博客首发地址将会是天地会的论坛,由于我是他们哪里的原创管理。所以我以后在发布博客首发地址将会天地会感兴趣的同学可以关注一下
http://bbs.9ria.com/forum.php?mod=forumdisplay&fid=318
如果没有看懂的同学可给我留言,我给给大家仔细讲解一下























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








