中国剩余定理

最新推荐文章于 2024-09-28 22:05:59 发布

御前带可乐侍卫

最新推荐文章于 2024-09-28 22:05:59 发布

阅读量791

点赞数 18

文章标签：算法

本文链接：https://blog.csdn.net/2301_76861619/article/details/141902638

版权

预备知识：

（1） $(a+b)\%c = (a\%c+b\%c)\%c$

（2）存在两个数： $m_1$ 和 $m_2$ ，设 $d$ 是 $gcd(m_1,m_2)$ ( $m_1$ 和 $m_2$ 的最大公约数)，则有：

$\frac{m_1m_2}{d} = [m_1,m_2]$ ( $[m_1,m_2]$ 是 $m_1$ 和 $m_2$ 的最小公倍数)

（3）如果一个数 $x$ 可能的数值为 $x+kx_0$ ，那么这个数的最小正整数解可以表示为 $(x\%x_0+x_0)\%x_0$

（4）在计算机中，负数模上负数的结果仍然是负数：

如 $-5\quad mod\quad 3 = -2$

整数解（算法原理不是这个）：

已知 $m_1$ , $m_2$ , $m_3$ ,..., $m_k$ 两两互质（有解的前提条件），求解下列方程组：

设 $M = m_1m_2...m_k$

设 $M_i = \frac{M}{m_i}$ （ $m_i$ 是 $m_1,m_2,...,m_k$ 中的任意一个 $m_i$ ）， $M_i$ 就是除 $m_i$ 外所有项的乘积

因为 $m_1$ , $m_2$ , $m_3$ ,..., $m_k$ 两两互质，所以 $M_i$ 和 $m_i$ 互质，那么运用逆元的概念：

必定存在一个 $x$ 满足 $M_ix \equiv 1(mod\quad m_i)$ ，这个 $x$ 就是 $M_i$ 模 $m_i$ 意义下的乘法逆元，一般记作： ${M_i}^{-1}$

公式解（不要问公式怎么推的）： $x = a_1M_1{M_1}^{-1}+a_2M_2{M_2}^{-1}+...+a_kM_k{M_k}^{-1}$

实例：

对于第一个方程： $x\equiv a_1(mod \quad m_1)$ ，将这个方程翻译一下，就是：

$x\quad mod\quad m_1 =a_1\quad mod \quad m_1$ ，将 $x$ 的公式解代入到方程中，那么就是：

$(a_1M_1{M_1}^{-1}+a_2M_2{M_2}^{-1}+...+a_kM_k{M_k}^{-1})mod\quad m_1 = (a_1M_1{M_1}^{-1}mod\quad m_1+a_2M_2{M_2}^{-1}mod\quad m_1 + ...+a_kM_k{M_k}^{-1}mod\quad m_1)mod\quad m_1$

因为根据逆元的定义： $M_1{M_1}^{-1}mod\quad m_1 = 1mod \quad m_1 = 1$ ，将其代入至上面的公式中：

$(a_1M_1{M_1}^{-1}mod\quad m_1+a_2M_2{M_2}^{-1}mod\quad m_1 + ...+a_kM_k{M_k}^{-1}mod\quad m_1)mod\quad m_1$

得到：

$(a_1+a_2M_2{M_2}^{-1}mod\quad m_1 + ...+a_kM_k{M_k}^{-1}mod\quad m_1)mod\quad m_1$

对于括号中的第二项：因为 $M_2$ 是除 $m_2$ 外的所有数的乘积，所以 $M_2mod\quad m_1$ 一定是0，对于其它项，也是一样的道理，因此计算过后上式就变为：

$a_1 mod\quad m_1$ （这是 $xmod\quad m_1$ 化简之后的式子，发现正好方程组的第一个方程成立）

再以同样的方式将 $x$ 的公式解代入至方程组的其他方程中，发现均符合，所以 $x$ 的公式解就是：

$x = a_1M_1{M_1}^{-1} + a_2M_2{M_2}^{-1} +...+a_kM_k{M_k}^{-1}$

如何求逆元？

（之前学的快速幂求逆元要求模上的数必须是质数，才可以用快速幂，但此时模上的数不一定是质数，因此需要用裴蜀定理和扩展欧几里得算法）：

将 ${M_i}^{-1}$ 看成 $x$ ，有公式： $M_1x\equiv 1(mod\quad m_1)$ ，将公式进行变形得到： $M_1x = m_1y+1$

（其中的 $y$ 是任意一个整数，当 $M_1$ 和 $m_1$ 互质时必定存在），设 $y^{'} = -y$ ，得到：

$M_1x+m_1y^{'} =1$ ，因为 $M_1$ 和 $m_1$ 互质，所以 $gcd(M_1,m_1) = 1$ ，所以 $M_1x+m_1y^{'} = gcd(M_1,m_1)$ ，这就是裴蜀定理的公式，采用扩展欧几里得算法进行求解

算法原理：

假设此时方程组中只有两个方程

$x \equiv a_1(mod\quad m_1)$

$x \equiv a_2(mod\quad m_2)$

将他们变形为：

$x = k_1m_1+a_1$

$x = k_2m_2+a_2$

可得 $k_1m_1+a_1 = k_2m_2+a_2$ ，等式变换一下，得到 $k_1m_1+k_2(-m_2) = a_2-a_1$

发现这是线性同余方程的形式（线性同余方程：http://t.csdnimg.cn/1itN4http://t.csdnimg.cn/1itN4http://t.csdnimg.cn/1itN4）

因此只要 $(m_1,-m_2)|a_2-a_1$ ，那么就一定可以求出一组 $k_1,k_2$ ，使得等式成立

求出特解后，可以由此推算出 $k_1$ 的所有解的形式： $k_1+k\frac{m_2}{d}$

和 $k_2$ 的所有解的形式： $k_2+k\frac{m_1}{d}$

（其中： $d$ 是 $m_1$ 和 $-m_2$ 的最大公约数； $k$ 是任意一个整数）

那么 $x$ 的所有解就可以表示为：（用 $k_1$ 表示）

$x = (k_1+k\frac{m_2}{d})m_1+a_1 = k_1m_1+a_1+k\frac{m_2m_1}{d}$

（用 $k_2$ 表示）

$x = (k_2+k\frac{m_1}{d})m_2+a_2 = k_2m_2+a_2+k\frac{m_2m_1}{d}$

因为 $k_1m_1+a_1 = k_2m_2+a_2$ ，所以两种表示形式下， $x$ 是相等的。

因为 $k_1$ 的所有解为 $k_1+k\frac{m_1m_2}{d}$ ，我们想要取得 $k_1$ 的最小正整数解，用这样的方式：

ll t = abs(m_2/d);
k_1 = (k_1%t + t)%t;

就可以得到 $k_1$ 的最小正整数解。

那么 $x = k_1m_1+a_1$ ，这个 $x$ 就是开始方程组的解。

根据 $x$ 的所有解的形式，得到： $x = (k_1m_1+a_1)+k\frac{m_1m_2}{d}$

发现得到的等式的形式和一开始方程组中的方程形式类似，因此我们将第一个方程中的 $a_1$ 更新为 $k_1m_1+a_1$ ， $m_1$ 更新为 $abs(\frac{m_1m_2}{d})$

这样的话，我们就将一开始方程组中的两个方程合并为了一个方程，并且用这个合并之后的方程替代了原本方程组中的第一个方程，如果方程组中还有第三个方程，就用这个新的第一个方程和第三个方程合并，再次得到一个新的方程，接下来就以此类推，直到方程组中没有剩下的方程了。

那么最后得到的 $x = k_1m_1+a_1$ ，就一定是方程组中所有方程的解，但不一定是最小的

所以还要求 $x$ 的最小正整数解：

所以将 $k_1 = 0$ ，那么 $x = a_1$ ，所以求 $x$ 的最小正整数解就是求 $a_1$ 的最小正整数解，根据预备知识（3）所以 $x$ 的最小正整数解可以表示为：

$(a_1\%m_1+m_1)\%m_1$

step1：

在循环外读入 $m_1$ 和 $a_1$ ，因为除了第一次循环 $m_1$ 和 $a_1$ 会作为原始方程组中的第一个方程中的数，之后的循环中， $m_1$ 和 $a_1$ 是作为之前所有方程的合并方程的数

（ $m_1$ 和 $a_1$ 起到了记录合并方程的作用）

step2：

开始循环

读入新的方程中的数 $m_2$ 和 $a_2$ ，结合第一个方程，得到一个线性同余方程（http://t.csdnimg.cn/1itN4），利用扩展欧几里得算法求出 $m_1$ 和 $-m_2$ 的最大公约数 $d$ 。

如果 $a_2-a_1$ 不能整除 $d$ ，说明这个线性同余方程无解，那么读入的两个方程就没有共同的解，推出循环

如果 $a_1-a_1$ 能够整除 $d$ ，说明这个线性同余方程一定有解。

（但是因为扩展欧几里得算法求出的 $k_1$ 满足的是 $k_1m_1+k_2(-m_2) = d$ ，所以要想得到满足 $k_1m_1+k_2(-m_2) = a_2-a_1$ ，要将求出的 $k_1$ 更新为 $k_1*{\frac{a_2-a_1}{d}}$ ）

step3：

根据上一个板块 算法原理 我们知道了 $k_1$ 的所有解的形式为 $k_1+k\frac{m_2}{d}$ ，因为题目要求的是 $x$ 的最小整数解，所以要求出 $k_1$ 所有解中的最小正整数解：

$(k_1\%t+t)\%t$ （注意： $t$ 是 $\frac{m_2}{d}$ 的绝对值形式，如果 $t$ 取到负值的话， $k_1$ 是无法取得最小正整数）

step4：

将更新之后的 $k_1$ 代入至第一个方程中（或者第二个方程）， $x = k_1m_1+a_1$ ，得到的 $x$ 就是初始两个方程的共同解

step5：

将 $a_1$ 更新为 $k_1m_1+a_1$ ，将 $m_1$ 更新为 $abs(\frac{m_2m_1}{d})$ ，这样就将方程组中的第一个方程的数更新为了原来的第一个方程和第二个方程的合并方程的数。

继续循环下去，不断将 $m_1$ 和 $a_1$ 更新为循环读入的所有方程的合并方程中的数。

step6：

直到循环结束，那么此时 $m_1$ 和 $a_1$ 就是方程组中所有方程的合并方程的中的两个数

那么最后一次循环中的 $x = k_1m_1+a_1$ 就是所有方程合并方程的解，自然就是整个方程组的解

step7：

为了确保 $x$ 是 $x$ 所有解中的最小正整数解，将 $k_1 = 0$ ，那么 $x = a_1$ ，所以求 $x$ 的最小正整数解就是求 $a_1$ 的最小正整数解，根据预备知识（3）所以 $x$ 的最小正整数解可以表示为：

$(a_1\%m_1+m_1)\%m_1$

题目如下：

给定 2n 个整数 a1,a2,…,an和 m1,m2,…,mn，求一个最小的非负整数 x，满足 ∀i∈[1,n],x≡ai(mod mi)

输入格式

第 1 行包含整数 n。

第 2…n+1 行：每 i+1 行包含两个整数 mi 和 ai，数之间用空格隔开。

输出格式

输出最小非负整数 x，如果 x 不存在，则输出 −1。

数据范围

$1\leqslant a_i \leqslant 2^{31}-1$
0≤mi<ai
1≤n≤25
所有 mi 的最小公倍数在 64 位有符号整数范围内。

代码如下：

#include<iostream>
#include<cstring>

using namespace std;

typedef long long ll;

int n;

ll exgcd(ll a,ll b,ll &x,ll &y)
{
    if (b == 0)
    {
        x = 1;
        y = 0;
        return a;
    }
    ll d = exgcd(b,a%b,x,y);
    ll tmp = x;
    x =y;
    y = tmp-a/b*y;
    return d;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    
    cin >> n;
    
    ll a_1,m_1;
    cin >>m_1 >> a_1;
    
    ll x = 0;
    
    for (int i = 0;i<n-1;++i)
    {
        ll m_2,a_2;
        cin >> m_2 >> a_2;
        
        ll k_1,k_2;
        ll d = exgcd(m_1,-m_2,k_1,k_2);
        
        if ((a_2-a_1)%d != 0)
        {
            x = -1;
            break;
        }
        
        k_1 = k_1*(a_2-a_1)/d;
        
        ll t = abs(m_2/d);
        k_1 = (k_1%t+t)%t;
        
        x = k_1*m_1+a_1;
        
        a_1 = k_1*m_1+a_1;
        m_1 = abs(m_1/d*m_2);
    }
    if (x !=-1)
        x = (a_1%m_1+m_1)%m_1;
        
    cout << x;
    return 0;
}

（1）为什么需要 ll t = abs(m_2/d) 这一步

因为题目要求的是求 $x$ 的最小正整数解，而 $x$ 的解的形式为 $k_1m_1+a_1$ ，所以要让 $k_1$ 取得尽可能小，也就是取得 $k_1$ 的最小正整数解，而 $k_1$ 的所有解的形式为 $k_1+k\frac{m_2}{d}$ ，那么就通过 $(k_1\%t+t)\%t$ （其中： $t = abs(m_2/d)$ ）的方式，得到 $k_1$ 的最小正整数解。

（对于这个求最小正整数解的公式，简单模拟一下就明白过程和为什么需要 $t = abs(m_2/d)$ 了

需要用到预备知识（4））

（2）为什么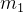 $m_1$ 要更新为 $abs(\frac{m_1m_2}{d})$ 要加abs

不会，背下来就完了。

但可以明确的是有没有 abs 对结果不会产生影响：

因为合并之后的方程的形式为： $x = k_1m_1+a_1+k\frac{m_1m_1}{d}$ ，我们将 $a_1$ 更新为 $k_1m_1+a_1$ ，将 $m_1$ 更新为 $abs(m_1/d*m_2)$

如果 $\frac{m_1m_2}{d}>0$ ，那么这个abs加不加都无所谓

如果 $\frac{m_1m_2}{d}<0$ ，那么加了这个abs后， $m_1$ 更新之后的值就会变为 $-\frac{m_2m_1}{d}$ ，和不加abs的更新值 $\frac{m_1m_2}{d}$ ，相差了 $2\frac{m_1m_2}{d}$ ，而合并方程中的 $k$ 是一个任意整数，因此 $k$ 可以适应 $m_1$ 更新之后的值的不同。