leetcode 51 N皇后

一、题目描述

二、解题思路

整体思路

画出本题的决策树，可以用回溯+剪枝的方法来解决这个问题。本题决策树的构造过程可以参考代码随想录视频这就是传说中的N皇后？ 回溯算法安排！| LeetCode：51.N皇后_哔哩哔哩_bilibili。

具体思路

一、剪枝策略

（1）摆放要求：在一个 n×n 的棋盘上放置 n 个皇后，使得任何两个皇后之间不能互相攻击；

（2）攻击条件(需要同时避免)：

<1>不能处于同一行；

<2>不能处于同一列；

<3>不能处于同一条主对角线（从左上角到右下角);

<4>不能处于同一条副对角线（从右上角到左下角);

（3）N皇后问题最核心的部分就是其独特的剪枝策略：

<1>不能在同一行。由于回溯是一行一行列举，所以可以满足这个条件；

<2>不能再同一列。可以定义bool向量Col，若Col[col]为false，则代表col列未摆放皇后。反之，则代表从来列已经摆放了皇后，不可以再在这列摆放皇后；

<3>不能处于同一条主对角线(从左上角到右下角)。以N=3为例子：

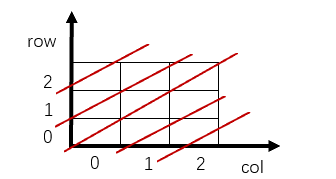
N=3时，主对角线有5条(为了便于抽象，我们粗略理解为2*n条)，这些主对角线的斜率都为1，截距b的范围为-(n-1)~n-1，这些主对角线的一般函数表达式为：

y=x+b -->  row=col+b -->  row-col=b 

所以在同一主对角线上的皇后的坐标row-col的截距b是相同的，我们可以使用布尔向量main_diagonal来记录截距b是否被使用（即当前主对角线是否已经摆放皇后）。由于截距b存在为负数的情况，而数组的下标必须为非负数，于是在等式两边都加上n，可以保证b+n为非负数：

row-col=b --> row-col+n=b+n

<4>能处于同一条副对角线（从右上角到左下角)。以N=3为例子：

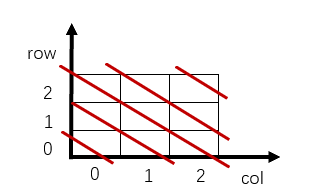
N=3时，副对角线有5条(为了便于抽象，我们粗略理解为2*n条)，这些主对角线的斜率都为-1，截距b的范围为0~n-1，这些主对角线的一般函数表达式为：

y=-x+b -->  row=-col+b -->  row+col=b 

所以在同一副对角线上的皇后的坐标row+col的截距b是相同的，我们可以使用布尔向量anti_diagonal来记录截距b是否被使用（即当前副对角线是否已经摆放皇后）。

二、函数逻辑

（1）函数功能：dfs函数用于从row行开始，尝试在col位置放置皇后，解决N皇后问题。

（2）递归出口：当row==n时，表示本次N皇后摆放完成，将path加入ret，然后return;

（3）函数体：处理每一层(row)

<1>从col=0到col=n-1循环，尝试在本行的每一列放置皇后；

<2>如果当前位置满足摆放皇后的条件(用Col、main_diagonal、anti_diagonal判断)，将path[row][col]修改为'Q'；

<3>再将当前位置对应的Col、main_diagonal、anti_diagonal值修改为true；

<4>dfs处理row+1行，处理完后回溯恢复现场，将当前位置修改为'.'，将对应的Col、main_diagonal、anti_diagonal值修改为false;

三、代码实现

class Solution {
    vector<vector<string>> ret;
    vector<string> path;
    //剪枝原则
    vector<bool> Col;
    vector<bool> main_diagonal;
    vector<bool> anti_diagonal;
public:
    vector<vector<string>> solveNQueens(int n) {
        //初始化path
        path=vector<string>(n,string(n,'.'));
        //空间优化
        Col.resize(n,false);
        main_diagonal.resize(2*n,false);
        anti_diagonal.resize(2*n,false);
        dfs(0,n);
        return ret;
    }
    void dfs(int row,int n){
        //递归出口
        if(row==n){
            ret.push_back(path);
            return ;
        }

        for(int col=0;col!=n;col++){
            if(!Col[col]&&!main_diagonal[row-col+n]&&!anti_diagonal[row+col]){
                path[row][col]='Q';
                Col[col]=main_diagonal[row-col+n]=anti_diagonal[row+col]=true;
                dfs(row+1,n);
                //恢复现场
                path[row][col]='.';
                Col[col]=main_diagonal[row-col+n]=anti_diagonal[row+col]=false;
            }
        }
    }
};