模式匹配---kmp算法

模式匹配--Kmp算法

暴力匹配

暴力匹配，既普通模式匹配，主串一个一个地与子串进行比对，一旦匹配失败就跳回主串原指针的下一个重新回溯，子串跳回第一个，重新开始匹配。

主串	B	A	B	C	B	F	D	A	B
下标	0	1	2	3	4	5	6	7	8

子串

B

C

B

主串原指针指向下标为0的字符‘B’，开始与子串第一个相等匹配，匹配发现相等，然后主串、子串都跳到下一个进行匹配。

主串	B	A	B	C	B	F	D	A	B
下标	0	1	2	3	4	5	6	7	8

子串

B

C

B

通过匹配发现不相等，就跳回主串原指针（下标为0的字符）的下一个（既下标为1的字符’A’重新回溯,注意这时主串原指针指向了下标为1的字符，子串又从第一个开始，重新开始匹配。

主串	B	A	B	C	B	F	D	A	B
下标	0	1	2	3	4	5	6	7	8

子串

B

C

B

通过匹配不难发现匹配失败，主串指针跳到下标为2的位置，子串还是指向第一个字符，又重新开始匹配。

主串	B	A	B	C	B	F	D	A	B
下标	0	1	2	3	4	5	6	7	8

子串

B

C

B

此时主串原指针指向下标下标为2的字符，匹配成功，然后主串、子串指针都跳到下一个进行匹配，但是原指针没有改变。

主串	B	A	B	C	B	F	D	A	B
下标	0	1	2	3	4	5	6	7	8

子串

B

C

B

以此找到子串的位置为下标为2的地方，但是返回的要是逻辑序号，既第3个位置。

代码 

#include<iostream>
#include<string>
using namespace std;
const int N = 100010, M = 1000010;
int n, m;
string s, p;
int main()
{
    cout << "主串长度为：";
    cin >> n;
    cout << "主串：";
    cin >> p;
    cout << "子串长度为：";
    cin >>m;
    cout << "子串：";
    cin >> s;
    int j = 0, i = 0;         //i,j分别扫描主串p和子串s
    while (i < n && j < m)    //主串和子串都没有扫完
    {
         if (p[i] == s[j] )
         {
             i++;
             j++;
         }
         else
         {
             i = i - (j - 1);
             j = 0;
         }
    }
    if (j>= m)
         cout<<"子串在主串的位置为："<<(i + 1 - m);
    else
         cout << "子串不在主串中";
}

通过代码发现此算法的时间复杂度为：

                            T=O(n*m)     n为主串的长度，m为子串的长度。

虽然此方法简单易懂，但是如果运气不好，到最后才发现匹配成功就会做不少的无用功，如图，此次时间复杂度达到O(n*m)，效率极低。

主串	A	A	A	A	A	A	A	A	B
下标	0	1	2	3	4	5	6	7	8

子串

A

A

A

B

kmp算法

求得next数组

为了减少回溯，提高执行效率，三位大佬们便研究出KMP算法，代码非常简洁，但是理解相对有点困难。

Kmp算法求得next数组，每次匹配失败，主串不再回溯，子串跳到与主串相匹配的位置，可以跳过一些不匹配的字符，而next数组就表示可以跳过的字符个数。

以这个为例：

主串	A	B	A	B	C	A	A	A	B
下标	0	1	2	3	4	5	6	7	8

子串

A

B

C

A

首先主串的前两个AB与子串AB匹配

主串	A	B	A	B	C	A	A	A	B
下标	0	1	2	3	4	5	6	7	8

子串

A

B

C

A

随后主串的下标为2的“A”与子串“C”不匹配，那么由于在此之前已经匹配过了，主串不动，子串第一个直接跳到与主串的下标为2的“A”进行匹配。

主串	A	B	A	B	C	A	A	A	B
下标	0	1	2	3	4	5	6	7	8

子串

A

B

C

A

随后依次匹配发现找到匹配位置

主串	A	B	A	B	C	A	A	A	B
下标	0	1	2	3	4	5	6	7	8

子串

A

B

C

A

那么我们该怎么表示出该跳过的字符长度呢，这就要引入最长前后缀的概念了，我们取next数组第一个为0（其实也有为-1，1的说法，为0的更好理解，在后续更好匹配）

首先前缀一定要包括最前面那一个，后缀一定要包括最后一个。

A              最长相等前后缀长度为0

AA               最长相等前后缀长度为1

AAA             最长相等前后缀长度为2

AAAB            最长相等前后缀长度为0

AAABA         最长相等前后缀长度为1

AAABAA      最长相等前后缀长度为2

AAABAAC     最长相等前后缀长度为0

那么以此生成子串的next数组

子串	A	A	A	B	A	A	C
next	0	1	2	0	1	2	0

再看abababc的next数组：

a         最长相等前后缀长度为0

ab       最长相等前后缀长度为0

aba     最长相等前后缀长度为1

abab    最长相等前后缀长度为2

ababa   最长相等前后缀长度为3

ababab  最长相等前后缀长度为4

abababc 最长相等前后缀长度为0

子串	a	b	a	b	a	b	c
next	0	0	1	2	3	4	0

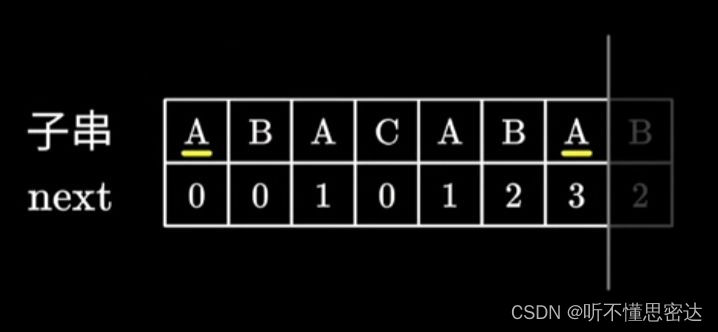
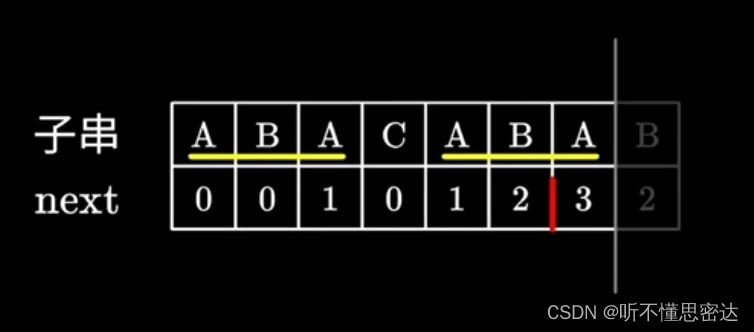
注意：最长相等前后缀

黄线画的是相等前后缀，但不是最长的，最长的相等前后缀应该是ABA,长度为3。

next数组算法

取两个指针i,j，j代表前缀指向，i代表扫描字符的后缀指向，指针j首先指向子串的第一个字符位置(既j=0),直接定义子串的第一个字符位置的next数组值为0（既next[0]=0），指针i指向子串的第二个字符位置(既i=1)，如果i，j指向的字符相等，就都往后移，next数组值+1，如果不相等就看前缀指向j的前一个next数组值，指针j就跳到指向j的前一个next数组值的物理序号，直到匹配到i，j指向的字符相等或者j=0。

next数组代码

具体的代码实现如下：

void get_Next(string s, int next[])

{

       int j = 0;

       next[0] = 0;                         //取next数组第一个为0

       for (int i = 1; i < s.size(); i++)   //子串未扫描完

       {     

              while (j > 0 && s[i] != s[j])           //前后缀不相等，前缀指针不为零的情况

                     j = next[j - 1];

              if (s[i] == s[j])

                     j++;                    //指针往后移，同时代表最长相等前后缀长度

                     ne[i] = j;                       //生成next数组

       }

}

匹配算法

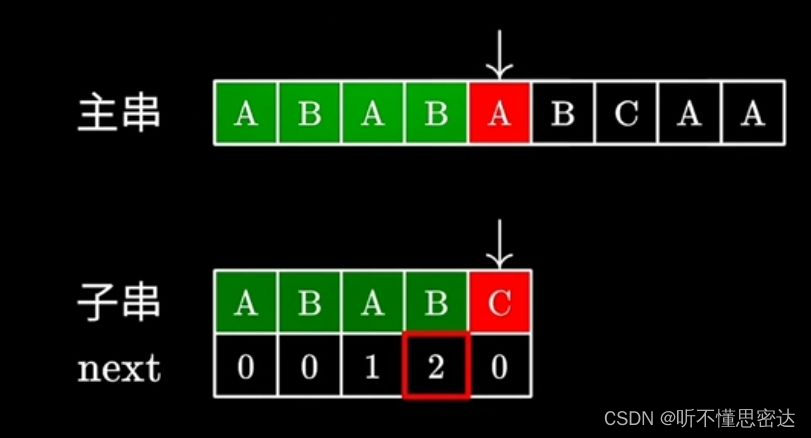
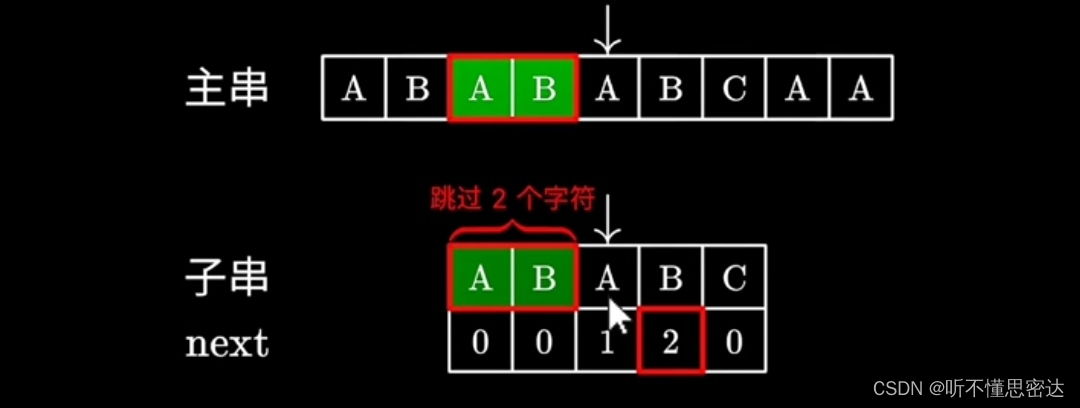
了解了next数组的原理，开始kmp匹配算法

取两个指针i，j,指针i指向主串第一个字符的位置，指针j指向子串的第一个位置，如果i，j指向的字符相等，则i，j都往后移动，如果不相等，则主串i指针不动。子串指针j跳到j前一个的next数组值，作为j指向子串的物理位置序号（既下标从0开始），知道匹配相等或者j为0。最后要返回的是子串在主串的逻辑序号（既下标从1开始）。

因此时间复杂度大大缩小

时间复杂度为：

          T=O(n+m)            n为主串的长度，m为子串的长度。

代码

具体代码实现如下：

int j = 0, i = 0;

       for (i = 0; i < n; i++)

       {

              while (p[i] != s[j] && j > 0)

                     j = next[j - 1];      //子串跳字符回溯

              if (p[i] = s[j])  

                       j++;

              if (j == m)

                     printf("%d", i - j + 2);//cout<<i-j+2<<" "    //要返回的是逻辑序号

       }

   return 0；

 总代码

最后kmp算法整体实现代码如下：

#include<iostream>
#include<string>
using namespace std;
const int N = 100010, M = 1000010;
int n, m;
int next[N];
string s, p;
void getNext(string s, int next[])
{
       int j = 0;
       next[0] = 0;   
       for (int i = 1; i < s.size(); i++)
       {     
              while (j > 0 && s[i] != s[j])   
                    j = next[j - 1];
              if (s[i] == s[j])
                     j++;
              next[i] = j;     
       }
}
int main()
{
    cout << "主串长度为：";
    cin >> n;
    cout << "主串：";
    cin >> p;
    cout << "子串长度为：";
    cin >>m;
    cout << "子串：";
    cin >> s;
       get_Next(s, next);
       int j = 0, i = 0;
       for (i = 0; i < n; i++)
       {
              while (p[i] != s[j] && j > 0)
                    j = next[j - 1];
              if (p[i] = s[j])  
                    j++;
              if (j == m)
                    printf("%d", i - j + 2);//cout<<i-j+2<<" "
       }
       return 0;
}