2025.3.6学习日志-CSDN博客

LeetCode-3 无重复子串

给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。

题目描述：

示例 1:

输入: s = "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2:

输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

示例 3:

输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
     请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

[分析]

核心思想：滑动窗口

使用一个map容器来保存每个字符的位置，通过滑动窗口，不断移动right右指针，每次移动后检索指向的元素是否在map里，如果存在则更新左指针位置，不存在则继续右移。

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        unordered_map<char,int> record;
        int left = 0,right = 0;
        int length = 0;
        while(right < s.size())
        {
            if(record.find(s[right]) != record.end())
            {
                left = max(left,record[s[right]] + 1);
            }
    
            record[s[right]] = right;
            length = max(length,right - left +1);
            right++;
        }

        return length;
        
    }
};

需要注意的点：

left = max(left,record[s[right]] + 1);

在更新左指针位置的时候要注意，当我们检测到right指针存在于map中时候，要使用max，原因如下：

如果 record[s[right]] + 1 比当前 left 还大，说明要把 left 更新到新的不重复起点。
如果 record[s[right]] + 1 比当前 left 小，说明 left 不能回退，保持原值。

CUDA内存模型

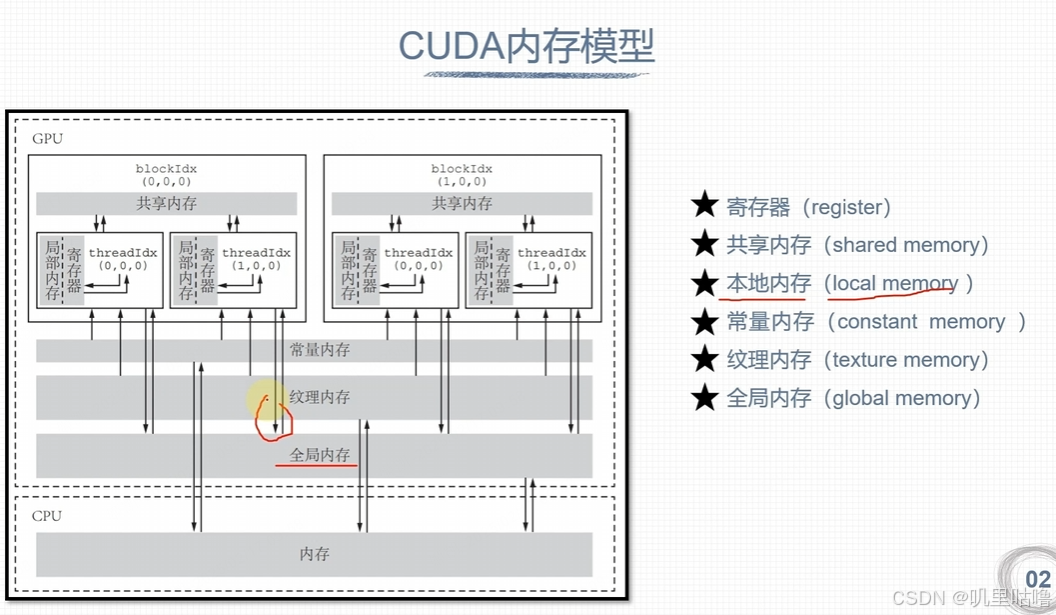
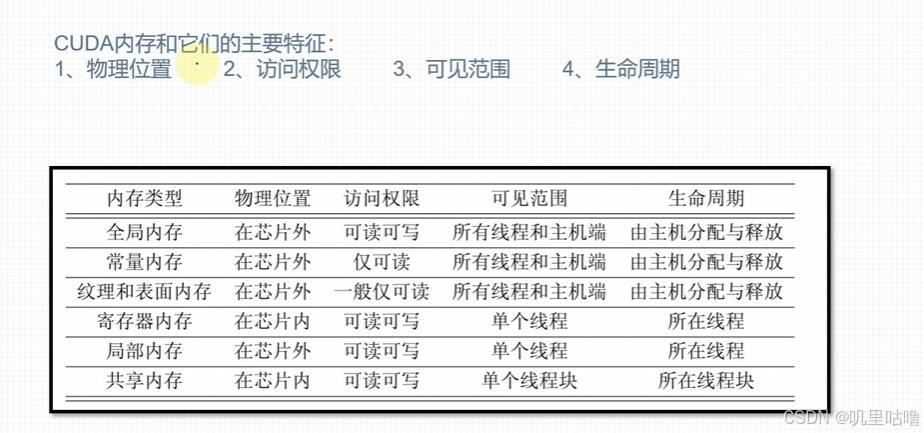
小测试：通过共享内存加速矩阵乘法运算：

代码链接（github）在MatrixMul文件夹中

cuda_learn/MatrixMul at main · Yoimiya-lover/cuda_learn

execution_v1的核函数如下：

    template <typename T>
    __global__ void matrixMulKernel(T* A, T* B, T* C,const int M, const int K, const int N) 
    {
        int row = blockIdx.y * blockDim.y + threadIdx.y;
        int col = blockIdx.x * blockDim.x + threadIdx.x;
        
        if (row < M && col < N) {
            float sum = 0.0f;
            for (int i = 0; i < K; i++) {
                sum += A[row * K + i] * B[i * N + col];
            }
            C[row * N + col] = sum;
        }
    }

execution_v2的核函数如下：

 template <typename T>
    __global__ void matrixMulkernel_v2(T* A, T* B, T* C,const int M, const int K, const int N)
    {
        int row = blockIdx.y * blockDim.y + threadIdx.y;
        int col = blockIdx.x * blockDim.x + threadIdx.x;

        int tx = threadIdx.x;
        int ty = threadIdx.y;

        __shared__ T SA[32][32];
        __shared__ T SB[32][32];
        int width =( K + blockDim.x -1 )/ blockDim.x;

        T Csum = 0;
        for (int ph = 0; ph < width; ph++) 
        {
            // 确保索引合法，避免越界访问
            if (row < M && (ph * blockDim.x + tx) < K) {
                SA[ty][tx] = A[row * K + (ph * blockDim.x + tx)];
            } else {
                SA[ty][tx] = 0.0f;
            }
    
            if ((ph * blockDim.x + ty) < K && col < N) {
                SB[ty][tx] = B[(ph * blockDim.x + ty) * N + col];
            } else {
                SB[ty][tx] = 0.0f;
            }
    
            __syncthreads();
    
            // 计算 C 的局部和
            for(int k = 0; k < blockDim.x; k++) {
                Csum += SA[ty][k] * SB[k][tx];
            }
    
            __syncthreads();
        }
    
        // 将计算结果写入全局内存
        if (row < M && col < N) {
            C[row * N + col] = Csum;
        }
    }

我们重点解释v2代码：

核心思想：把A,B矩阵变为分块矩阵

SA,SB为共享内存，共享内存访问速度大于全局内存，一般我们设为32*32的固定大小

 int width =( K + blockDim.x -1 )/ blockDim.x

width为每个线程处理矩阵的行数，使用向上取整

            if (row < M && (ph * blockDim.x + tx) < K) {
                SA[ty][tx] = A[row * K + (ph * blockDim.x + tx)];
            } else {
                SA[ty][tx] = 0.0f;
            }

将需要使用的矩阵加载到共享内存中

             if (row < M && (ph * blockDim.x + tx) < K) {
                SA[ty][tx] = A[row * K + (ph * blockDim.x + tx)];
            } else {
                SA[ty][tx] = 0.0f;
            }
    
            if ((ph * blockDim.x + ty) < K && col < N) {
                SB[ty][tx] = B[(ph * blockDim.x + ty) * N + col];
            } else {
                SB[ty][tx] = 0.0f;
            }
    
            __syncthreads();

注意！！最后一定要线程同步，否则不同步后计算将会出错。

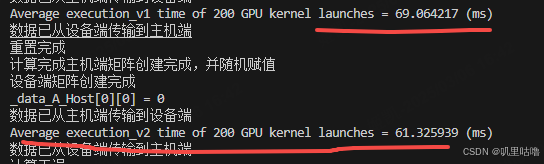
测试结果：

在做：2000 *3000 和3000 *5000 大小矩阵的结果如下