Java基础——递归思想-CSDN博客

一、递归思想

1.1 什么是递归

递归是指方法调用自身的编程技巧，通过将复杂问题分解为相似的子问题来求解。

// 最简单的递归示例（会导致栈溢出！）
public void endlessRecursion() {
    endlessRecursion(); // 无限递归，最终StackOverflowError
}

所以使用递归的时候，递归一定要有出口，否者会出现内存溢出。

工作原理是调用栈（Call Stack）机制

每次方法调用都会在栈内存中创建栈帧（Stack Frame），包含

1.2 递归练习

递归练习1

package com.lkbhua.Algorithm.sort;

public class RecursionTest {
    public static void main(String[] args) {
        /*利用递归思想：求1-100之间的和*/

        // 大问题拆解为小问题
        // 1-100之间的和 = 100 + (1-99之间的和)
        // 1-99之间的和 = 99 + (1-98之间的和)
        // 1-98之间的和 = 98 + (1-97之间的和)
        // 依次类推------------
        // 1-1之间的和 = 1 (递归的出口)
        int sum = getSum(100);
        System.out.println(sum);
    }

    public static int getSum(int n){
        if(n == 1){
            return 1;
        }

        // 递归调用
        return n + getSum(n - 1);
    }
}

递归练习2

package com.lkbhua.Algorithm.sort;

public class RecursionTest2 {
    public static void main(String[] args) {
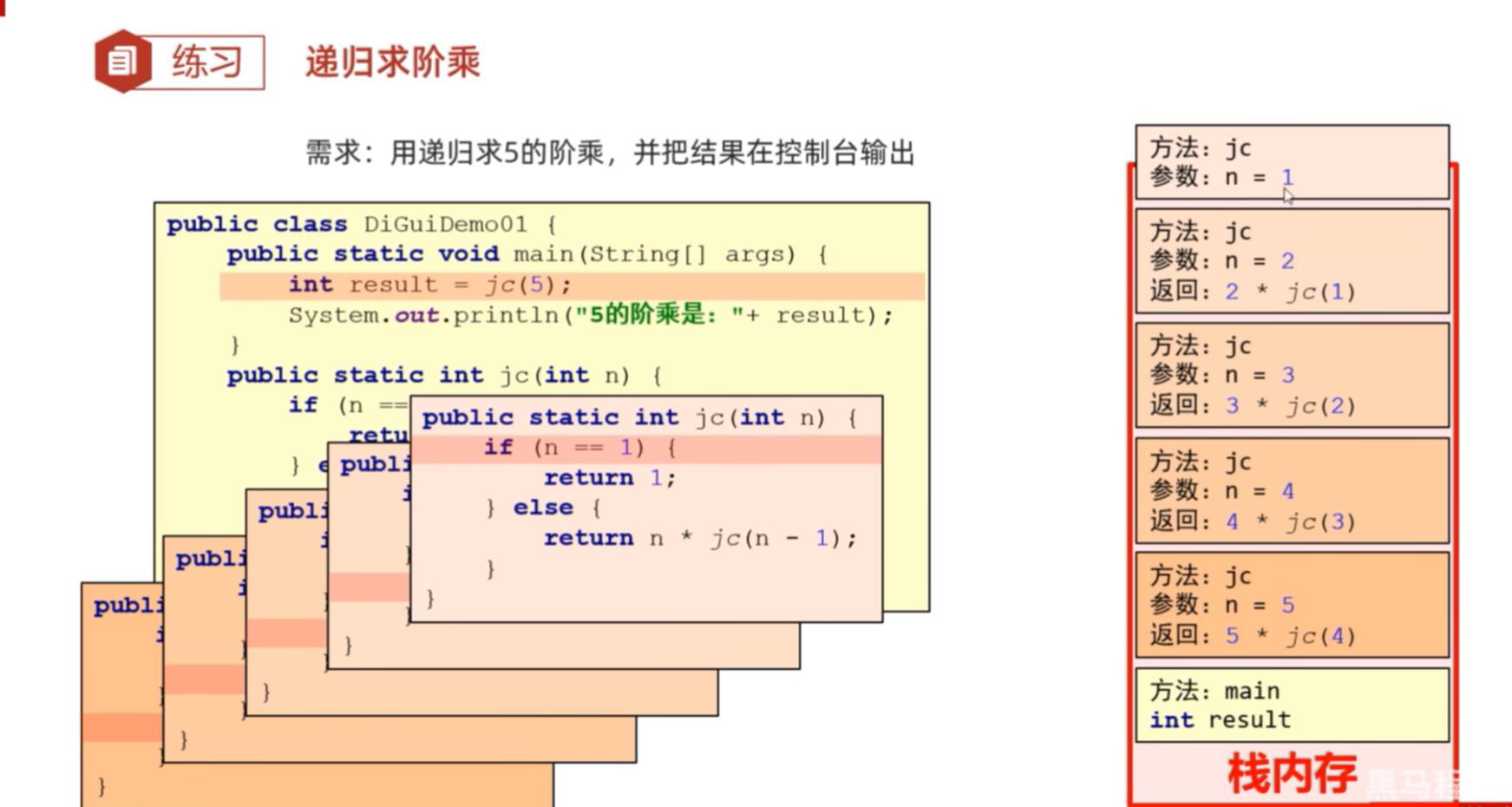
        /*求5的阶乘利用递归*/

        // 大事化小
        // 5！= 4! * 5
        // 4！= 3! * 4
        // 3！= 2! * 3
        
        System.out.println(factorial(5));

    }
    public static int factorial(int n){
        if(n == 1){
            return 1;
        }
        return n * factorial(n - 1);
    }
}

1.3 优缺点

优点	说明
代码简洁	自然表达问题的数学定义
逻辑清晰	符合人类思维模式，易于理解
问题分解	自动处理复杂的状态管理

缺点	说明
性能开销	每次调用都有栈帧创建和销毁的开销
栈溢出风险	递归深度过大导致 `StackOverflowError`
调试困难	调用栈深时难以追踪
内存占用	每个栈帧占用内存，可能导致内存不足