对称二叉树

一、题目

给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

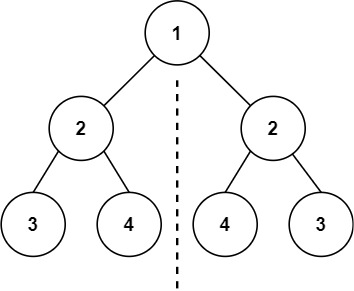
输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

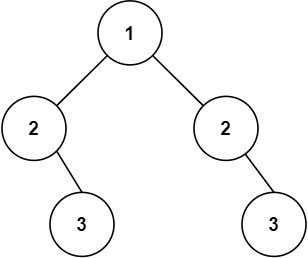
输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

• 树中节点数目在范围 [1, 1000] 内
• -100 <= Node.val <= 100

二、源代码

bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
    if (p == NULL || q == NULL) {
        return p == q;
    }
    return p->val == q->val && isSameTree(p->left, q->right) && isSameTree(p->right, q->left);
}

bool isSymmetric(struct TreeNode* root) {
    return isSameTree(root->left, root->right);
}

三、解题思路

1.核心逻辑：对称二叉树的定义

一棵二叉树是对称的，需满足：

根节点的左子树和右子树互为“镜像”

镜像的定义：结构对称（对应位置节点要么都存在，要么都不存在），且对应节点的值相等

2.代码解析

（1）辅助函数 isSameTree

功能：判断两棵树是否互为镜像（而非完全相同）。

边界处理：若两个节点中有一个为空，只有两者都为空（结构对称）时返回true；否则返回false（结构不对称）。

递归判断：若两节点都非空，需满足 3 个条件：

当前节点值相等（p->val == q->val）；

p的左子树与q的右子树对称（镜像关系的关键：左对右）；

p的右子树与q的左子树对称（镜像关系的关键：右对左）。

（2）主函数 isSymmetric

功能：判断整棵树是否对称。

对称二叉树的核心是“根节点的左子树与右子树互为镜像”，因此直接调用isSameTree比较根节点的左子树（root->left）和右子树（root->right）即可。

四、总结

1.核心逻辑：

对称二叉树的关键是“根节点的左子树与右子树互为镜像”。镜像需满足：结构对称（对应位置节点同时存在或同时不存在），且对应节点值相等。

2.函数分工：

isSymmetric（主函数）：直接判断根节点的左子树与右子树是否互为镜像，通过调用isSameTree实现。

isSameTree（辅助函数）：判断两棵树是否互为镜像（非完全相同）。