【深度学习|学习笔记】从背景→公式→性质→梯度→何时用哪一个→数值稳定性与常见坑方面描述sigmoid和softmax函数！

【深度学习|学习笔记】从背景→公式→性质→梯度→何时用哪一个→数值稳定性与常见坑方面描述sigmoid和softmax函数！

【深度学习|学习笔记】从背景→公式→性质→梯度→何时用哪一个→数值稳定性与常见坑方面描述sigmoid和softmax函数！

---

---

欢迎铁子们点赞、关注、收藏！
祝大家逢考必过！逢投必中！上岸上岸上岸！upupup

大多数高校硕博生毕业要求需要参加学术会议，发表EI或者SCI检索的学术论文会议论文。详细信息可扫描博文下方二维码 “学术会议小灵通”或参考学术信息专栏：https://blog.csdn.net/2401_89898861/article/details/148877490

---

1) 背景与直觉

• sigmoid 用于“二分类/单神经元输出”的概率映射：把一个实数 logit 映到 (0,1)。
• softmax 用于“多分类（互斥）/多神经元输出”的概率归一化：把一个 logits 向量 映到 K 维概率单纯形（各分量∈(0,1)，且总和=1）。

从优化角度看：

• 二分类逻辑回归 ←→ sigmoid + 二分类交叉熵。
• 多分类逻辑回归 ←→ softmax + 多分类交叉熵。

2) 定义与公式

Sigmoid（logistic 函数）

定义：

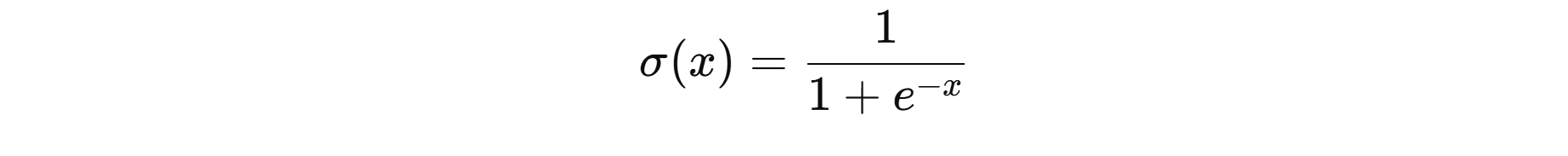
性质：

• 输出范围 (0,1)；对称点在 $x=0\Rightarrow \sigma (0)=0.5$；单调递增、两端饱和。

导数：

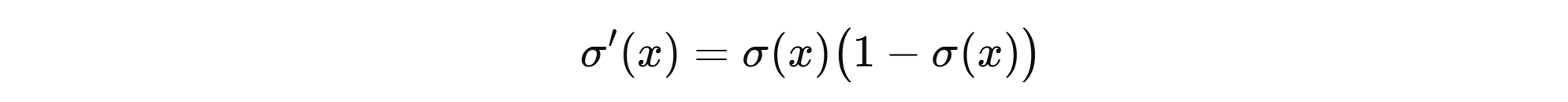
导数：损失（带 logits 的二分类交叉熵）（数值稳定写法，标签 $y\in 0,1$，logit = z）

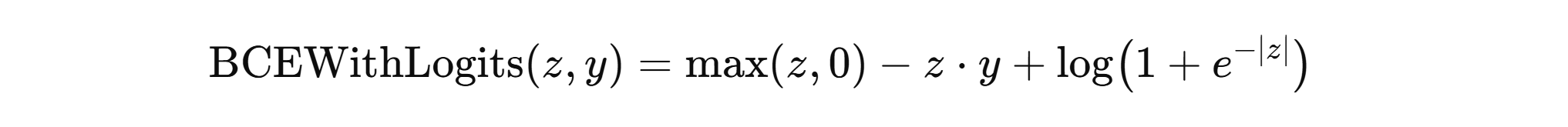
Softmax

• 对 K 维 logits 向量 $z=(z_1,\dots ,z_K)$：
  

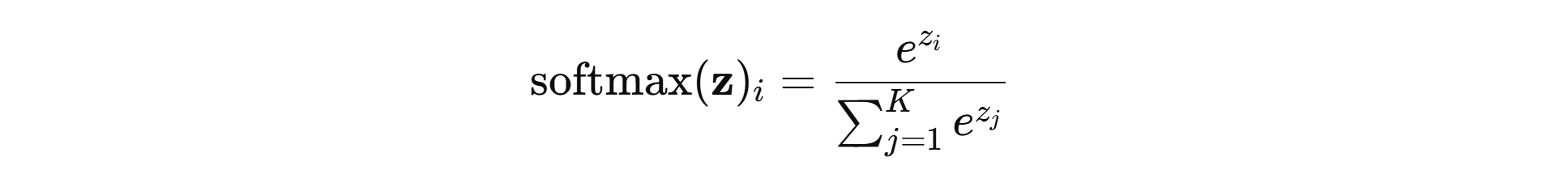
性质：

• 输出为概率分布，所有分量相加为 1。
• 雅可比矩阵（梯度）：

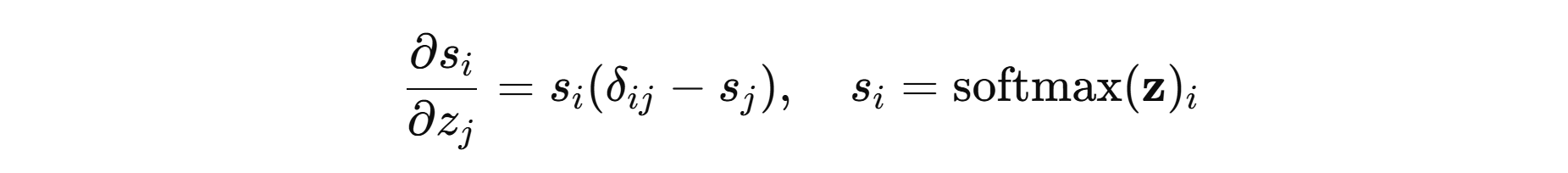
• 损失（多分类交叉熵）（数值稳定写法，真类索引为 $y$）：
  
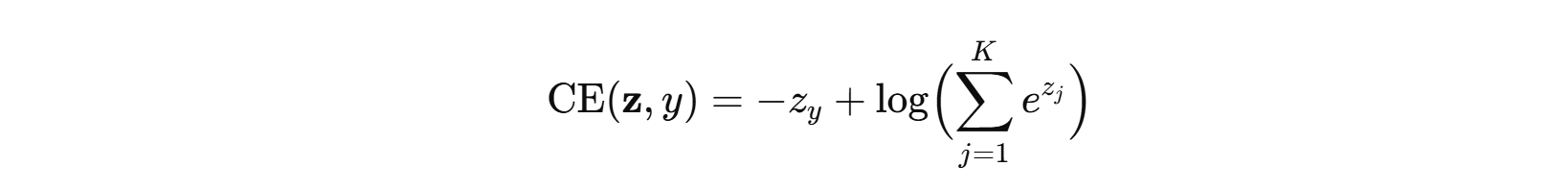
• 常用 log-sum-exp trick：先减去 m a x ( z ) max(z)