动手学运动规划: 2.2 3次样条曲线(Cubic Spline)

自动驾驶小白说

于 2024-09-29 09:03:34 发布

阅读量514

点赞数 12

分类专栏：动手学运动规划文章标签：算法自动驾驶运动规划

本文链接：https://blog.csdn.net/2403_86993842/article/details/142626696

版权

动手学运动规划专栏收录该内容

14 篇文章 0 订阅

订阅专栏

我自狂歌空度日, 飞扬跋扈为谁雄. — 亮剑楚云飞

🏰代码及环境配置：请参考0.2 环境配置和代码运行 | 动手学运动规划!

上一节说到多项式曲线的缺点: 不管是多少阶的多项式, 能够表达的曲线始终是有限的. 那么有没有什么简单的办法能够克服这个缺陷呢? 插值样条就是一种简单有效的方法.

2.2.1 3次样条曲线定义

3次样条曲线(Cubic Spline), 是一种通过一系列三次多项式来逼近给定数据点集的方法。每个多项式定义在两个相邻的数据点之间，且满足在数据点处及其一阶导数和二阶导数都连续的条件。

简单的说, 它在每两个采样点之间, 构造了一个3次多项式. 这样只要采样点和点之间距离足够近, 理论上可以表达任何曲线.

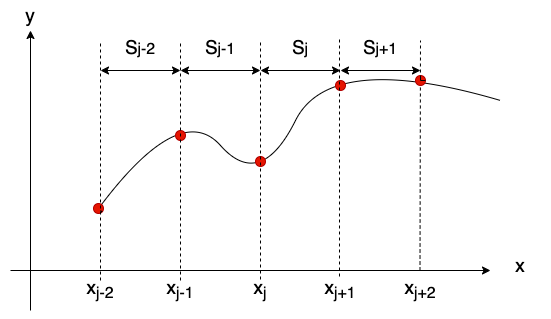
我们先从1维的3次样条开始解释, 比如图上的这5个点, 我们在每两个点之间构造一个3次多项式.那么有如下定义:

$\begin{align*} S_j(x)=a_j+b_j\left(x-x_j\right)+c_j\left(x-x_j\right)^2&+d_j\left(x-x_j\right)^3 \\ x_j < x < x_{j+1} \end{align*}$

$x_j$ 和 $x_{j+1}$ 是第j段样条的起点和终点, $a_j, b_j, c_j, d_j$ 是第j段样条的参数.

很好理解的是, 每段样条有起点和终点的这些约束:

$\begin{align*} S_j\left(x_j\right)&=y_j \\ S_j\left(x_{j+1}\right)&=S_{j+1}\left(x_{j+1}\right)=y_{j+1} \\ S_j^{\prime}\left(x_{j+1}\right)&=S_{j+1}^{\prime}\left(x_{j+1}\right)\\ S_j^{\prime \prime}\left(x_{j+1}\right)&=S_{j+1}^{\prime \prime}\left(x_{j+1}\right) \end{align*}$

以及第一个点和最后一个点, 我们给的2阶导约束:

$S_0^{\prime \prime}(0)=S_{n+1}^{\prime \prime}\left(x_n\right)=0$

2.2.2 3次样条曲线参数求解

带入方程求解样条曲线的参数, 求解 $a_j$ :

$a_j=y_j$

求解 $c_j$ :

将各个样条方程统一放到 $A, B$ 矩阵中, 求解线性方程组.

$c_j=B \\ \begin{gathered} A=\left[\begin{array}{cccccc} 1 & 0 & 0 & 0 & \cdots & 0 \\ h_0 & 2\left(h_0+h_1\right) & h_1 & 0 & \cdots & 0 \\ 0 & h_1 & 2\left(h_1+h_2\right) & h_2 & \cdots & 0 \\ 0 & 0 & h_2 & 2\left(h_2+h_3\right) & \cdots & 0 \\ 0 & 0 & 0 & h_3 & \ddots & \\ \vdots & \vdots & & & & \\ 0 & 0 & 0 & \cdots & 0 & 1 \end{array}\right] \\ \\ B=\left[\begin{array}{c} 0 \\ \frac{3}{h_1}\left(a_2-a_1\right)-\frac{3}{h_0}\left(a_1-a_0\right) \\ \vdots \\ \frac{3}{h_{n-1}}\left(a_n-a_{n-1}\right)-\frac{3}{h_{n-2}}\left(a_{n-1}-a_{n-2}\right) \\ 0 \end{array}\right] \end{gathered}\\ \\ where \ h_i=x_{i+1}-x_i$