【数据结构初阶】--二叉树(五)

原创 于 2025-07-31 07:29:42 发布 · 1w 阅读 · 35 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#c语言 #数据结构 #经验分享 #笔记 #其他

 🔥个人主页：@草莓熊Lotso

🎬作者简介：C++研发方向学习者

📖个人专栏： 《C语言》 《数据结构与算法》《C语言刷题集》《Leetcode刷题指南》

⭐️人生格言：生活是默默的坚持，毅力是永久的享受。  

前言： 通过前面几篇博客我们已经完成了前中后序的接口实现，我们现在开始需要进行其它二叉树常用方法的实现，比如二叉树节点个数，叶子节点个数等。还是和之前一样分部分实现，最后再展示全部的代码。

目录

一.求二叉树节点个数

代码实现： 

test.c： 

二.求二叉树叶子节点个数

代码实现：

test.c： 

 三.求二叉树第k层节点个数

代码实现： 

test.c： 

 四.求二叉树的深度/高度

 代码实现：

test.c： 

 五.二叉树查找值为x的节点

代码实现：

test.c：

 六.二叉树的销毁 

代码实现：

 七.代码展现

Tree.h：

Tree.c：

test.c：

一.求二叉树节点个数

--我们先来实现一个求二叉树的节点个数的接口，在正式开始之前我们先把上次写的代码里的test.c中创建树的代码优化一下，这样方便后续操作

#include"Tree.h"

BTNode* buyNode(char x)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	newnode->data = x;
	newnode->left = newnode->right = NULL;
	return newnode;
}
BTNode* CreateTree()
{
	BTNode* nodeA = buyNode('A');
	BTNode* nodeB = buyNode('B');
	BTNode* nodeC = buyNode('C');
	BTNode* nodeD = buyNode('D');
	BTNode* nodeE = buyNode('E');
	BTNode* nodeF = buyNode('F');

	nodeA->left = nodeB;
	nodeA->right = nodeC;
	nodeB->left = nodeD;
	nodeC->left = nodeE;
	nodeC->right = nodeF;

	return nodeA;
}

void test1()
{
	BTNode* root = CreateTree();

	//前中后序遍历
	//PreOrder(root);
	//InOrder(root);
	//PostOrder(root);
}

int main()
{
	test1();
	return 0;
}

--优化完之后，我们就可以开始实现求二叉树节点个数的接口了 

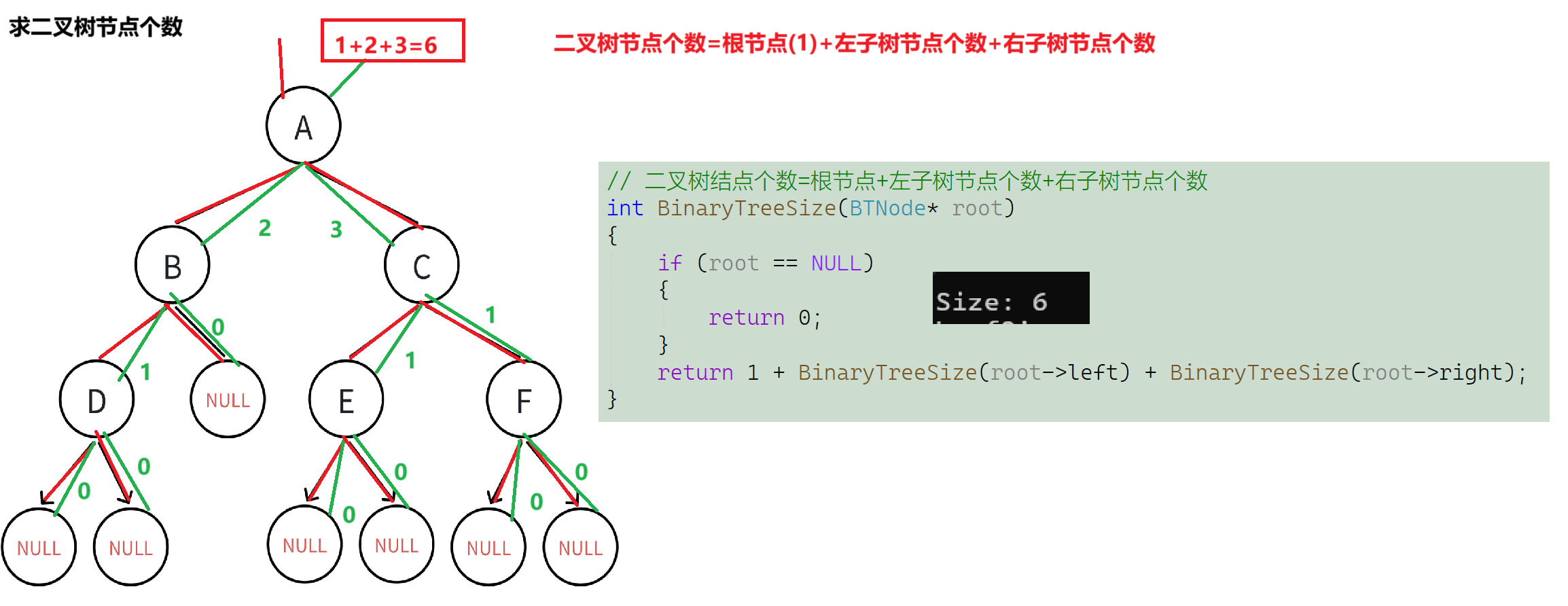
  •  二叉树结点个数=根节点+左子树结点个数+右子树结点个数

代码实现： 

// 二叉树结点个数=根节点+左子树节点个数+右子树节点个数
int BinaryTreeSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}

    图示如下：

    test.c： 

    #include"Tree.h"

BTNode* buyNode(char x)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	newnode->data = x;
	newnode->left = newnode->right = NULL;
	return newnode;
}
BTNode* CreateTree()
{
	BTNode* nodeA = buyNode('A');
	BTNode* nodeB = buyNode('B');
	BTNode* nodeC = buyNode('C');
	BTNode* nodeD = buyNode('D');
	BTNode* nodeE = buyNode('E');
	BTNode* nodeF = buyNode('F');

	nodeA->left = nodeB;
	nodeA->right = nodeC;
	nodeB->left = nodeD;
	nodeC->left = nodeE;
	nodeC->right = nodeF;

	return nodeA;
}

void test1()
{
	BTNode* root = CreateTree();

	//前中后序遍历
	//PreOrder(root);
	//InOrder(root);
	//PostOrder(root);

	//二叉树结点个数
	printf("Size: %d\n", BinaryTreeSize(root));
}

int main()
{
	test1();
	return 0;
}

    --测试完成，打印出来没有问题，退出码为0 

    二.求二叉树叶子节点个数

    --二叉树的叶子节点就是左右孩子都为空的节点

    • 二叉树叶子节点个数=左子树叶子节点个数+右子树叶子节点个数

    代码实现：

    // 二叉树叶子结点个数=左子树叶子节点个数+右子树节点个数
int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	//判断是否为叶子节点（没有左右孩子）
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}

	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

    图示如下： 

    test.c： 

    #include"Tree.h"

BTNode* buyNode(char x)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	newnode->data = x;
	newnode->left = newnode->right = NULL;
	return newnode;
}
BTNode* CreateTree()
{
	BTNode* nodeA = buyNode('A');
	BTNode* nodeB = buyNode('B');
	BTNode* nodeC = buyNode('C');
	BTNode* nodeD = buyNode('D');
	BTNode* nodeE = buyNode('E');
	BTNode* nodeF = buyNode('F');

	nodeA->left = nodeB;
	nodeA->right = nodeC;
	nodeB->left = nodeD;
	nodeC->left = nodeE;
	nodeC->right = nodeF;

	return nodeA;
}

void test1()
{
	BTNode* root = CreateTree();

	//前中后序遍历
	//PreOrder(root);
	//InOrder(root);
	//PostOrder(root);

	//二叉树结点个数
	printf("Size: %d\n", BinaryTreeSize(root));
	//二叉树叶子结点个数
	printf("LeafSize: %d\n", BinaryTreeLeafSize(root));
}

int main()
{
	test1();
	return 0;
}

    --测试完成，打印没有问题，退出码为0

     三.求二叉树第k层节点个数

    --当k==1时当前节点就是第k层节点

    • 二叉树第k层节点个数=左子树第k-1层节点个数+右子树第k-1层节点个数

    代码实现： 

    // 二叉树第k层节点个数=左子树第K-1层节点个数+右子树第k-1层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	if (root == NULL)
	{
		return 0;
	}
	//判断是否为第k层
	if (k == 1)
	{
		return 1;
	}
	//每次注意要k-1
	return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

    图示如下： 

    test.c： 

    #include"Tree.h"

BTNode* buyNode(char x)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	newnode->data = x;
	newnode->left = newnode->right = NULL;
	return newnode;
}
BTNode* CreateTree()
{
	BTNode* nodeA = buyNode('A');
	BTNode* nodeB = buyNode('B');
	BTNode* nodeC = buyNode('C');
	BTNode* nodeD = buyNode('D');
	BTNode* nodeE = buyNode('E');
	BTNode* nodeF = buyNode('F');

	nodeA->left = nodeB;
	nodeA->right = nodeC;
	nodeB->left = nodeD;
	nodeC->left = nodeE;
	nodeC->right = nodeF;

	return nodeA;
}

void test1()
{
	BTNode* root = CreateTree();

	//前中后序遍历
	//PreOrder(root);
	//InOrder(root);
	//PostOrder(root);

	//二叉树结点个数
	printf("Size: %d\n", BinaryTreeSize(root));
	//二叉树叶子结点个数
	printf("LeafSize: %d\n", BinaryTreeLeafSize(root));
	//第k层节点个数
	printf("K Size: %d\n", BinaryTreeLevelKSize(root,3));
}

int main()
{
	test1();
	return 0;
}

    --测试完成，打印没有问题，退出码为0

     四.求二叉树的深度/高度

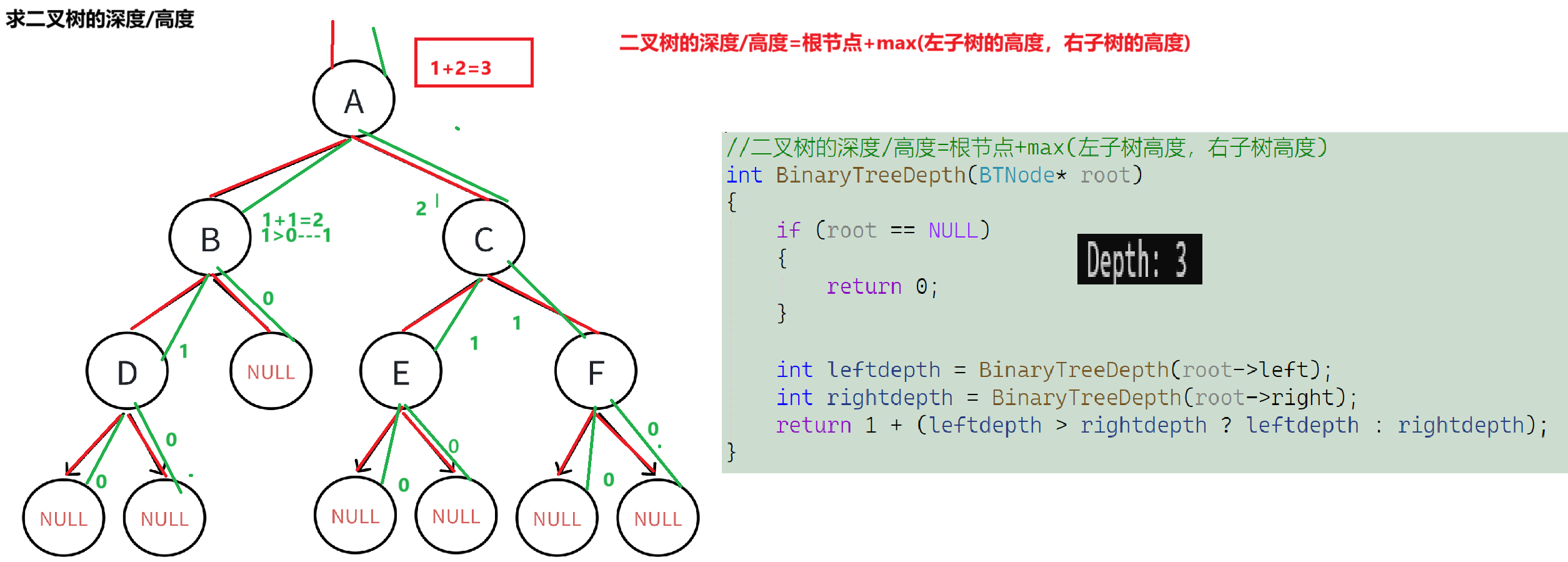
    • 二叉树的高度=根节点+max(左子树的高度，右子树的高度)

     代码实现：

    //二叉树的深度/高度=根节点+max(左子树高度，右子树高度)
int BinaryTreeDepth(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}

	int leftdepth = BinaryTreeDepth(root->left);
	int rightdepth = BinaryTreeDepth(root->right);
	return 1 + (leftdepth > rightdepth ? leftdepth : rightdepth);
}

    图示如下：

    test.c： 

    #include"Tree.h"

BTNode* buyNode(char x)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	newnode->data = x;
	newnode->left = newnode->right = NULL;
	return newnode;
}
BTNode* CreateTree()
{
	BTNode* nodeA = buyNode('A');
	BTNode* nodeB = buyNode('B');
	BTNode* nodeC = buyNode('C');
	BTNode* nodeD = buyNode('D');
	BTNode* nodeE = buyNode('E');
	BTNode* nodeF = buyNode('F');

	nodeA->left = nodeB;
	nodeA->right = nodeC;
	nodeB->left = nodeD;
	nodeC->left = nodeE;
	nodeC->right = nodeF;

	return nodeA;
}

void test1()
{
	BTNode* root = CreateTree();

	//前中后序遍历
	//PreOrder(root);
	//InOrder(root);
	//PostOrder(root);

	//二叉树结点个数
	printf("Size: %d\n", BinaryTreeSize(root));
	//二叉树叶子结点个数
	printf("LeafSize: %d\n", BinaryTreeLeafSize(root));
	//第k层节点个数
	printf("K Size: %d\n", BinaryTreeLevelKSize(root,3));
	//二叉树的深度/高度
	printf("Depth: %d\n", BinaryTreeDepth(root));
}

int main()
{
	test1();
	return 0;
}

    --测试完成，打印没有问题，退出码为0

     五.二叉树查找值为x的节点

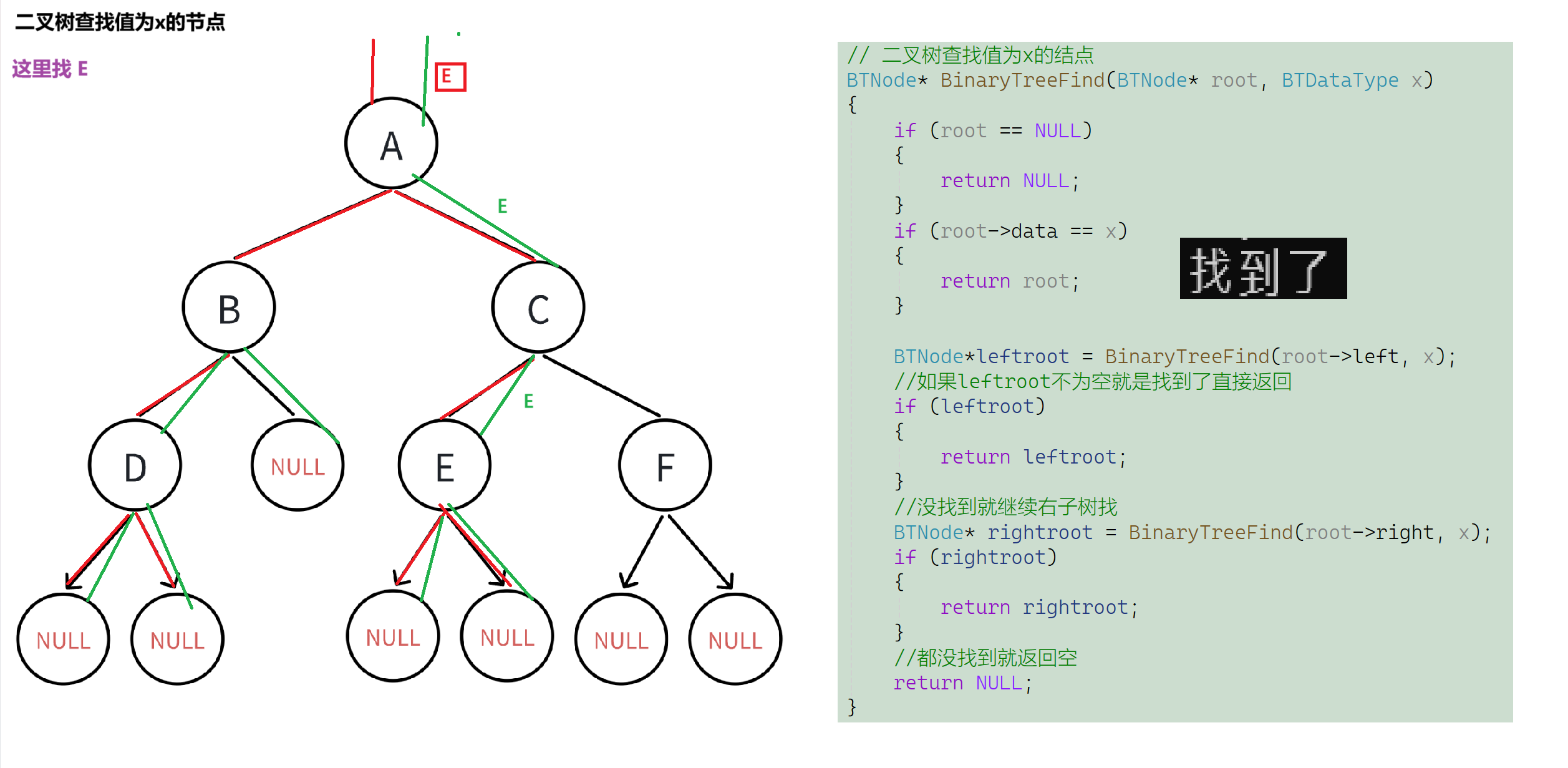
    --递归查找，找到了就返回当前节点，如果是在左子树中找到就直接返回，没找到继续来到右子树找，最好都没找到就返回NULL

    代码实现：

    // 二叉树查找值为x的结点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->data == x)
	{
		return root;
	}

	BTNode*leftroot = BinaryTreeFind(root->left, x);
	//如果leftroot不为空就是找到了直接返回
	if (leftroot)
	{
		return leftroot;
	}
	//没找到就继续右子树找
	BTNode* rightroot = BinaryTreeFind(root->right, x);
	if (rightroot)
	{
		return rightroot;
	}
	//都没找到就返回空
	return NULL;
}

    图示如下： 

    test.c：

    #include"Tree.h"

BTNode* buyNode(char x)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	newnode->data = x;
	newnode->left = newnode->right = NULL;
	return newnode;
}
BTNode* CreateTree()
{
	BTNode* nodeA = buyNode('A');
	BTNode* nodeB = buyNode('B');
	BTNode* nodeC = buyNode('C');
	BTNode* nodeD = buyNode('D');
	BTNode* nodeE = buyNode('E');
	BTNode* nodeF = buyNode('F');

	nodeA->left = nodeB;
	nodeA->right = nodeC;
	nodeB->left = nodeD;
	nodeC->left = nodeE;
	nodeC->right = nodeF;

	return nodeA;
}

void test1()
{
	BTNode* root = CreateTree();

	//前中后序遍历
	//PreOrder(root);
	//InOrder(root);
	//PostOrder(root);

	//二叉树结点个数
	printf("Size: %d\n", BinaryTreeSize(root));
	//二叉树叶子结点个数
	printf("LeafSize: %d\n", BinaryTreeLeafSize(root));
	//第k层节点个数
	printf("K Size: %d\n", BinaryTreeLevelKSize(root,3));
	//二叉树的深度/高度
	printf("Depth: %d\n", BinaryTreeDepth(root));
	//二叉树查找值为x的结点
	BTNode* pos = BinaryTreeFind(root, 'E');
	if (pos)
	{
		printf("找到了\n");
	}
	else {
		printf("没找到\n");
	}
}

int main()
{
	test1();
	return 0;
}

    --测试完成，找的到E，退出码为0

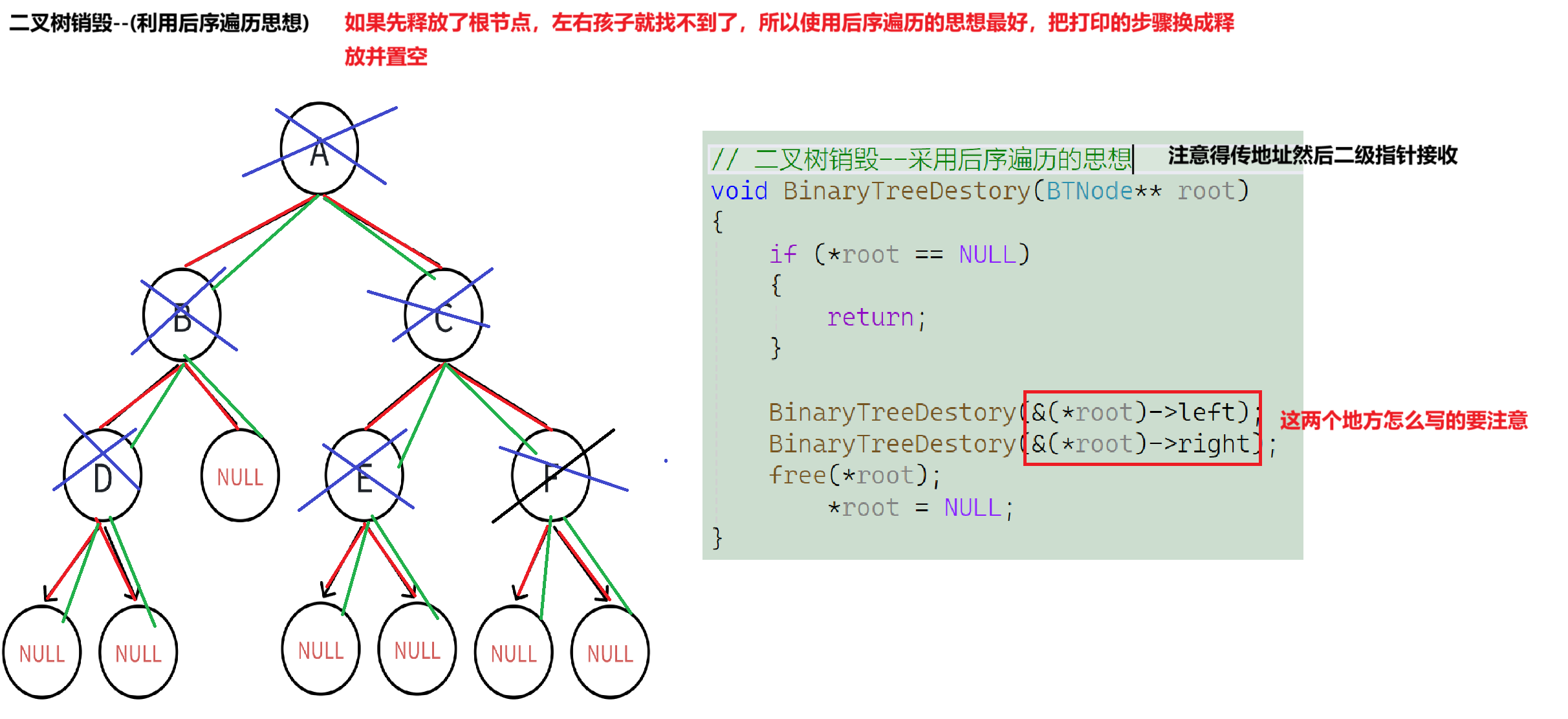
     六.二叉树的销毁 

    --由于提前释放根节点无法找到其左右节点，所以我们得采用后续遍历的思想，最后处理根节点，

    还有这里得传地址，后续的使用也需要注意一下写法。

    代码实现：

    // 二叉树销毁--采用后序遍历的思想
void BinaryTreeDestory(BTNode** root)
{
	if (*root == NULL)
	{
		return;
	}

	BinaryTreeDestory(&(*root)->left);
	BinaryTreeDestory(&(*root)->right);
	free(*root);
		*root = NULL;
}

    图示如下：

     七.代码展现

    Tree.h：

    #pragma once
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>

typedef char BTDataType;
typedef struct BinaryNode
{
	BTDataType data;
	struct BinaryNode* left;//左孩子
	struct BinaryNode* right;//右孩子
}BTNode;

//前序遍历
void PreOrder(BTNode* root);

//中序遍历
void InOrder(BTNode* root);

//后序遍历
void PostOrder(BTNode* root);

// 二叉树结点个数
int BinaryTreeSize(BTNode* root);

// 二叉树叶子结点个数
int BinaryTreeLeafSize(BTNode* root);

// 二叉树第k层结点个数
int BinaryTreeLevelKSize(BTNode* root, int k);

//二叉树的深度/高度
int BinaryTreeDepth(BTNode* root);

// 二叉树查找值为x的结点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);

// 二叉树销毁
void BinaryTreeDestory(BTNode** root);

    Tree.c：

    #include"Tree.h"

//前序遍历
void PreOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	//根左右
	printf("%c ", root->data);
	PreOrder(root->left);
	PreOrder(root->right);
}

//中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}

	//左根右
	InOrder(root->left);
	printf("%c ", root->data);
	InOrder(root->right);
}

//后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}

	//左右根
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%c ", root->data);
}

// 二叉树结点个数=根节点+左子树节点个数+右子树节点个数
int BinaryTreeSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}

// 二叉树叶子结点个数=左子树叶子节点个数+右子树节点个数
int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	//判断是否为叶子节点（没有左右孩子）
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}

	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

// 二叉树第k层节点个数=左子树第K-1层节点个数+右子树第k-1层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	if (root == NULL)
	{
		return 0;
	}
	//判断是否为第k层
	if (k == 1)
	{
		return 1;
	}
	//每次注意要k-1
	return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

//二叉树的深度/高度=根节点+max(左子树高度，右子树高度)
int BinaryTreeDepth(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}

	int leftdepth = BinaryTreeDepth(root->left);
	int rightdepth = BinaryTreeDepth(root->right);
	return 1 + (leftdepth > rightdepth ? leftdepth : rightdepth);
}

// 二叉树查找值为x的结点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->data == x)
	{
		return root;
	}

	BTNode*leftroot = BinaryTreeFind(root->left, x);
	//如果leftroot不为空就是找到了直接返回
	if (leftroot)
	{
		return leftroot;
	}
	//没找到就继续右子树找
	BTNode* rightroot = BinaryTreeFind(root->right, x);
	if (rightroot)
	{
		return rightroot;
	}
	//都没找到就返回空
	return NULL;
}

// 二叉树销毁--采用后序遍历的思想
void BinaryTreeDestory(BTNode** root)
{
	if (*root == NULL)
	{
		return;
	}

	BinaryTreeDestory(&(*root)->left);
	BinaryTreeDestory(&(*root)->right);
	free(*root);
		*root = NULL;
}

    test.c：

    #include"Tree.h"

BTNode* buyNode(char x)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	newnode->data = x;
	newnode->left = newnode->right = NULL;
	return newnode;
}
BTNode* CreateTree()
{
	BTNode* nodeA = buyNode('A');
	BTNode* nodeB = buyNode('B');
	BTNode* nodeC = buyNode('C');
	BTNode* nodeD = buyNode('D');
	BTNode* nodeE = buyNode('E');
	BTNode* nodeF = buyNode('F');

	nodeA->left = nodeB;
	nodeA->right = nodeC;
	nodeB->left = nodeD;
	nodeC->left = nodeE;
	nodeC->right = nodeF;

	return nodeA;
}

void test1()
{
	BTNode* root = CreateTree();

	//前中后序遍历
	//PreOrder(root);
	//InOrder(root);
	//PostOrder(root);

	//二叉树结点个数
	printf("Size: %d\n", BinaryTreeSize(root));
	//二叉树叶子结点个数
	printf("LeafSize: %d\n", BinaryTreeLeafSize(root));
	//第k层节点个数
	printf("K Size: %d\n", BinaryTreeLevelKSize(root,3));
	//二叉树的深度/高度
	printf("Depth: %d\n", BinaryTreeDepth(root));
	//二叉树查找值为x的结点
	BTNode* pos = BinaryTreeFind(root, 'E');
	if (pos)
	{
		printf("找到了\n");
	}
	else {
		printf("没找到\n");
	}
	// 二叉树销毁
	BinaryTreeDestory(&root);
}

int main()
{
	test1();
	return 0;
}

    往期回顾：

    【数据结构初阶】--树和二叉树先导篇

    【数据结构初阶】--二叉树(二)

    【数据结构初阶】--二叉树(三)

    【数据结构初阶】--二叉树(四)

    结语：在这篇博客中我们一起实现了二叉树的大部分常用接口，后面还有一个判断是否为完全二叉树和一个层序遍历的实现。如果文章对你有帮助的话，欢迎评论，点赞，收藏加关注，感谢大家的支持。

    二叉树，什么是叶子节点
    weixin_42720316的博客
    10-06 3万+
    1，树的深度：树中节点的最大层数即树的高度或深度 2，节点的度，一个节点拥有的子树数 3，叶子节点：度为0的节点 满二叉树：所有层的节点数都达到最大 完全二叉树：除最后一层不满外，其余层的都达到该层的最大节点数，最后如果不满，该层所有节点都全部靠左排 二叉树三种遍历方式： 前序遍历：先遍历根节点，再遍历左节点，最后遍历右节点 中序遍历：先遍历左节点，再遍历根节点，最后遍历右节点 后...
    数据结构入门-6-二叉树
    ifeng
    04-22 1304
    二叉树的入门
    【数据结构】二叉树
    YoungMLet的博客
    06-14 400
    二叉树的简单实现，前序，中序和后序，以及常见问题
    数据结构之二叉树
    m0_63635730的博客
    02-10 842
    数据结构之二叉树
    二叉树的概念、分类和性质
    星空
    04-21 1万+
    1、二叉树的概念 二叉树：每个节点最多有两个分支（分支的度小于2）的树结构，可为空树。 根节点：一棵树最上面的节点称为根节点。 左右子树：某个节点的左分支叫做左子树，右分支叫做右子树。 左右孩子：某个节点的左、右分支的根节点叫做该节点的左、右孩子。 兄弟节点：具有相同父节点的节点互为兄弟节点。 节点的度：节点拥有的子树数。 叶子节点：没有任何子节点的节点称为叶子节点。 内部节点：非叶子节点称为内...
    初阶数据结构之---二叉树链式结构（二叉树的构建，二叉树的前序，中序，后序和层序遍历，计算二叉树结点个数，第k层结点个数，叶子结点个数，判断是否为完全二叉树）
    2303_79329831的博客
    03-21 1752
    本篇博客围绕二叉树的遍历，结点个数计算以及数值查找等内容展开。关于二叉树更多有趣的内容还远远不止这些，不过再次深入时就会以C++的方式来给大家呈现了。
    初阶数据结构之---二叉树的顺序结构-堆
    2303_79329831的博客
    03-09 1528
    本篇博客带大家认识了一下树和堆，但这里只是带大家稍微看了看堆的实现。关于堆的内容其实还有很多，topk问题，堆排序，优先级队列中会更深入的带领大家去了解和使用堆，在下一篇数据结构中，会更深入的挖掘一些堆的应用，并计算一下其时间复杂度，让大家体会到堆的魅力。
    《数据结构初阶》一般二叉树题解-递归写法
    m0_62171658的博客
    04-13 1785
    关于普通二叉树的递归写法
    【初阶数据结构和算法】二叉树顺序结构---堆的定义与实现(附源码)
    最新发布
    hdxbufcbjuhg的博客
    11-30 3137
    【初阶数据结构和算法】初识树与二叉树的概念以及堆和完全二叉树之间的关系堆的本质是一颗完全二叉树，只是它的要求比完全二叉树更加严格，它要求每颗子树的根节点都是当前子树的最大值或最小值，当根节点是最大值时，它就是一个大根堆，当根节点是最小值时，它就是一个小根堆在上篇文章中我们也提到了，存储完全二叉树可以使用数组，存储非完全二叉树可以使用链表，而堆就是一种特殊的完全二叉树，所以堆的存储我们就使用数组，也就是顺序表的形式，如图：int size;}HP;
    【初阶数据结构】实现顺序结构二叉树-＞堆（附源码）
    braveact的博客
    11-02 1091
    文章目录。
    二叉树大总结
    m0_56987404的博客
    05-24 1010
    树的基本概念
    数据结构——二叉树
    mooooonster_QG的博客
    01-30 1048
    树形结构：有向无环图 树是图的一种树形结构有一个根节点没有回路A下面没有其他节点既不是根节点，也不是叶子节点的 普通节点树 中有最多叉的节点有多少个插叉，这棵树的度就为多少树最深有几层 深度就为几。
    【数据结构】二叉树 二叉树的深度优先遍历和广度优先遍历 完全二叉树和满二叉树的性质 二叉树的节点个数以及叶子节点个数
    qq_59702185的博客
    09-03 1539
    设二叉树的根节点所在的层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的根节点，然后从左到右访问第二层上的节点，以此类推，自上而下，自左至右逐层访问树的节点的过程就是层序遍历，也称为广度优先遍历。因为我们定义了一个全局的size，在我们计算了节点为A的节点个数时，得到的大小是5，但是在计算节点为B的节点个数为8,。但是，如果我们知道多线程的时候，程序在运行时，可能有多个进程在同时进行，我们就无法保证在求一个节点的数时的节点前，先把size赋值为0了。看下面的代码就很好的解决了这个问题。
    【数据结构】二叉树的节点数，叶子数，第K层节点数，高度，查找x节点，判断是否为完全二叉树等方法
    luhaoran814的博客
    09-20 4428
    二叉树的节点数，叶子数，第K层节点数，高度，查找x节点，判断是否为完全二叉树等方法
    39-二叉树的性质总结
    网络安全
    07-05 3460
    1. 性质1 性质1：非空二叉树上叶子节点数等于双分支节点数加1。   1. 假设二叉树上叶子节点数为n0n0n_0，单分支节点数为n1n1n_1，双分支节点数为n2n2n_2，则总的节点数n=n0+n1+n2n=n0+n1+n2n = n_0 + n_1 + n_2   我们仔细观察上图就能发现，二叉树中，叶子节点总共有4个（D，E，F，H），单分支节点数1个（G），双分支节点数总共3...
    数据结构（十四） -- C语言版 -- 树 - 二叉树的叶子节点、深度、拷贝等
    青椒*^_^*凤爪爪的博客
    05-31 5543
    本文中所有设计的代码均通过测试，并且在功能性方面均实现应有的功能。 设计的代码并非全部公开，部分无关紧要代码并没有贴出来。 如果你也对此感兴趣、也想测试源码的话，可以私聊我，非常欢迎一起探讨学习。 由于时间、水平、精力有限，文中难免会出现不准确、甚至错误的地方，也很欢迎大佬看见的话批评指正。 嘻嘻。。。。 。。。。。。。。收！
    带你全面的了解二叉树
    华为云官方博客
    09-24 1540
    摘要：日常生活中，很多事物都可以用树来描述，例如书的目录、工作单位的组织架构等等。树是计算机中非常重要的一种数据结构，树存储方式可以提高数据的存储、读取效率。
    完全二叉树的叶子节点数公式_二叉树基础知识
    热门推荐
    weixin_39960145的博客
    11-23 3万+
    一、二叉树定义二叉树是每个节点最多有两个子树的树结构，即二叉树中不存在度大于二的节点。并且，二叉树的子树有左右之分，其次序不能颠倒。二、二叉树的性质在二叉树的第i层上最多有2^(i-1)个结点深度为k的二叉树最多有2^(i)-1个结点对任意一个二叉树，若度为2的结点数为n2，叶子结点数为n0，则满足n0=n2+1具有n个结点的完全二叉树的深度为 [log2 n]+1，[]表示下取整三、三种遍历方式...
    评论 8
    添加红包

    请填写红包祝福语或标题

    个

    红包个数最小为10个

    元

    红包金额最低5元

    当前余额3.43元 前往充值 >
    需支付：10.00元
    成就一亿技术人!
    领取后你会自动成为博主和红包主的粉丝 规则
    hope_wisdom
    发出的红包
    实付元
    使用余额支付
    点击重新获取
    扫码支付
    钱包余额 0

    抵扣说明：

    1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
    2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

    余额充值