CSP二叉树通关秘籍 ①

对于考CSP(中国计算机学会非专业级别软件能力认证)的同学们对于二叉树这个东西并不陌生，他常常在考试中占那么一题，而对于尚未理解二叉树的同学，二叉树的几种遍历和画图可谓十分困难。那么，如何正确、快速理解二叉树呢？

1、二叉树是什么

二叉树（Binary tree）是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式，即使是一般的树也能简单地转换为二叉树，而且二叉树的存储结构及其算法都较为简单，因此二叉树显得特别重要。二叉树特点是每个节点最多只能有两棵子树，且有左右之分。

看起来有点抽象是吗，其实它的形态有点像倒过来的毕达哥拉斯树。以个节点最多可以有两条分支，左边的边可以叫做左子树或者左孩子，右边的同理。

2、二叉树的公式

一般来讲，一颗满二叉树(左右枝都是满的，不存在只有一条边的情况)的通用公式是

2^k-1

这个无需追其原理，考试时列方程即可，注意结果向上取整。

3、二叉树的遍历

一般来讲，二叉树的遍历有三：先序遍历(也称前序遍历)、中序遍历、后序遍历。一般的，考试时会给出一下两种情况：

        先序遍历和中序遍历

        后序遍历和中序遍历

需要注意的是，如果只知道一棵树的先序和后序遍历，是无法直接得到这颗树的图像。

而一般的，

        先序遍历的顺序是：根 -> 左 -> 右（这里指根节点、左子树和右子树）

        中序遍历的顺序是：左 -> 根 -> 右

        后序遍历的顺序是：左 -> 右 -> 根

甭管为啥，只是乌龟的屁股（龟腚）根据大多数人的习惯而定，记住就行。

考试时，我们需要根据已知的遍历画出二叉树，从而推出另一种遍历，具体如何去做呢？看个例题：

已知某二叉树的先序遍历是 ABDCE，中序遍历是 BDAEC，则该二叉树的后序遍历是什么？

我们通过公式 根 -> 左 -> 右 可以得知这颗树的根节点应该是A，那么我们在题目上做一个标记：BDAEC，这样我们可以清晰得区分树的左子树和右子树，分别是BD和EC。继续拆开来看，由于B在先序遍历先于D出现，由于 根 -> 左 -> 右 的公式，B应该是根节点，回到中序遍历中，以B为根节点，D在B的右边，所以D就是B的右子树。同理，右边的C先出现，故C为根节点，E在C的左侧，故E为C的左子树。画出的图像是这样的

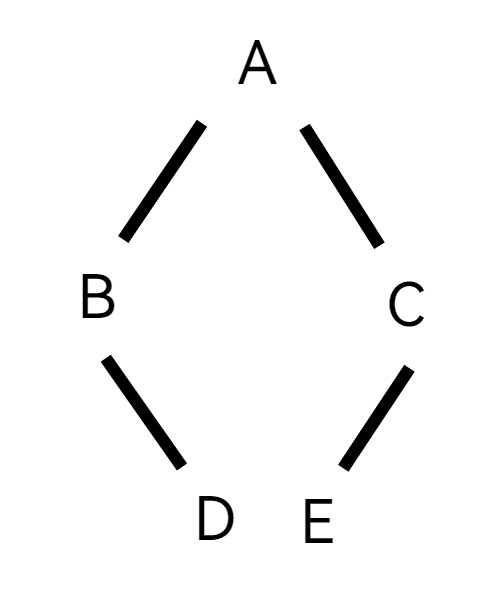
我们再根据后序遍历来对二叉树进行遍历得到：DBECA，至此，我们便可以总结出一套规律：我们要想知道先序或后序，要先画出二叉树的图像，才能对其进行遍历，从而解题。

这是第一章，后面回更新第二章，作者本人也是学者，文章中难免出现错误的情况如发现错误，望大佬们及时指正，谢谢大家！

---