图的DFS遍历：像侦探一样敲门遍历

一、先搞懂：图到底是个啥？（人话版）

你以为数据结构里的 “图” 是画的流程图？No No No！它其实是个 “人际关系网”—— 比如代码里的 A、B、C 九个节点，就像你的九个朋友，而arc[i][j]=1就代表 “这俩朋友认识”（无向边就是互相认识，不像微信单方面好友）。

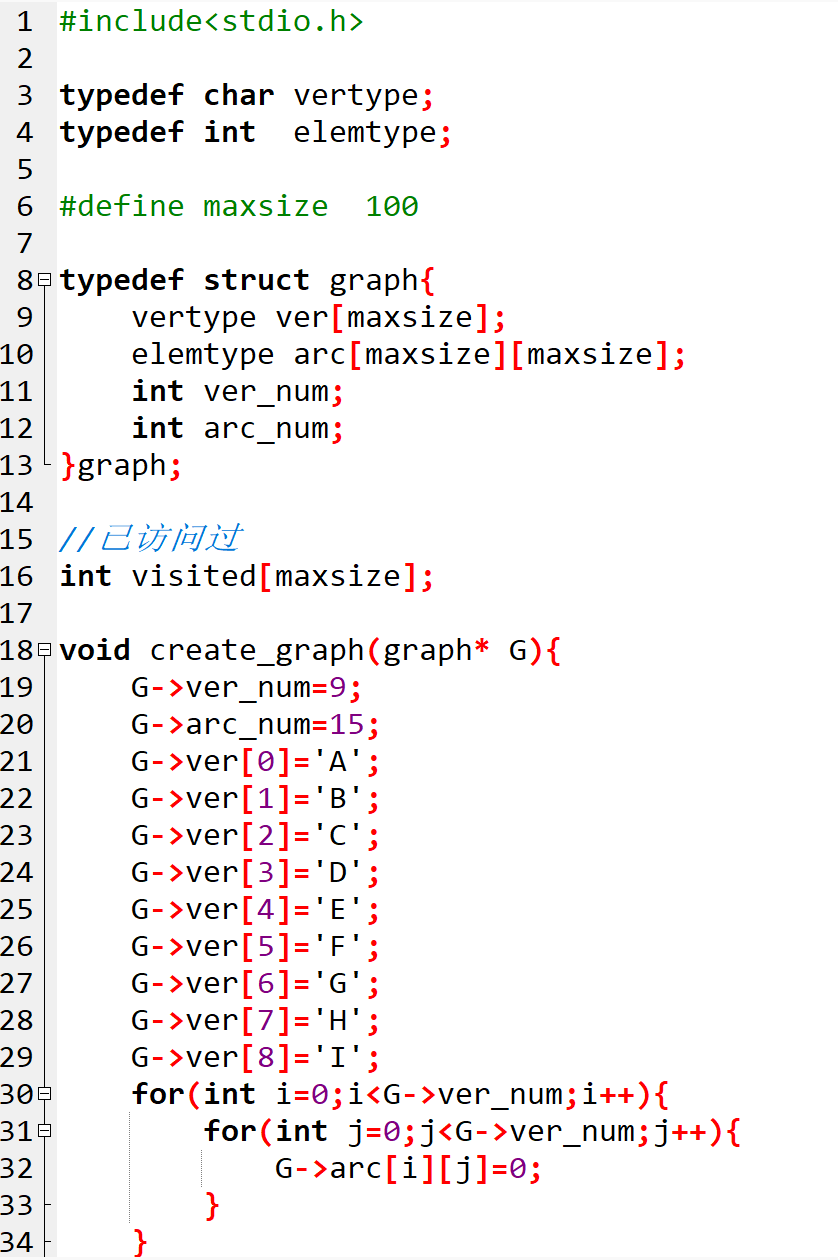
看看代码里的create_graph函数：9 个节点（A-I）、15 条边，比如 A 认识 B 和 F，B 认识 C、G、I…… 这就是一个典型的 “社交网络图”，而我们要做的，就是不重复、不遗漏地拜访所有朋友—— 这就是 “图的遍历”。

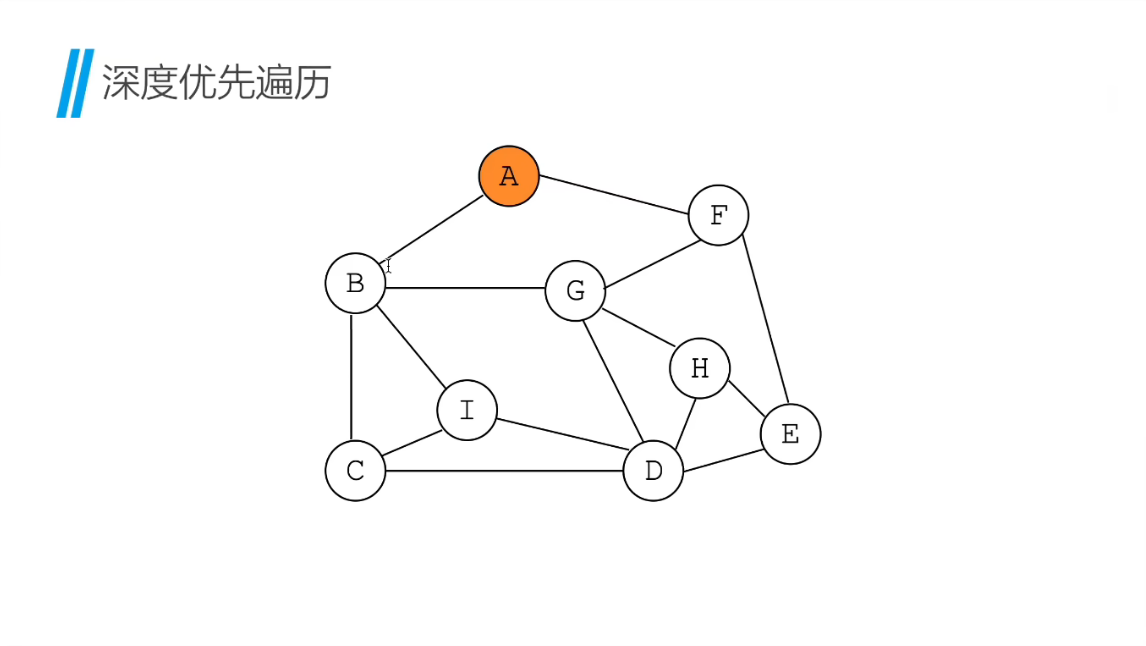
二、DFS：深度优先 = 一条路走到黑的侦探

遍历图有两种主流玩法，今天主角是DFS（深度优先遍历） ，它的核心逻辑堪称 “一根筋式破案”：

想象你是个侦探，要走访所有嫌疑人（节点）。你从 A 家出发，进门就问：“你认识谁还没被问过？”A 说 “我认识 B 和 F”，你二话不说先冲去 B 家（不纠结选谁，先选一个走到底）。到了 B 家，B 说 “我认识 C、G、I”，你又扎进 C 家…… 就这么 “一条路走到头”，直到某个节点的所有朋友都被问过了，再回头找下一个没走访的分支。

这就是 DFS 的精髓：优先往深走，走不动了再回头，像极了迷宫里不撞南墙不回头的探险家！

三、代码拆解：原来 DFS 这么简单！

结合你给的代码，咱们用 “侦探破案” 的视角拆解每一步：

1. 准备工作：给侦探配装备

int visited[maxsize]; // 记录谁被问过（0=没问，1=问过）

这就像侦探的 “走访记录本”，避免重复问同一个人（不然嫌疑人会烦的！）。main 函数里先把所有记录初始化 0，相当于 “所有人都没走访”。

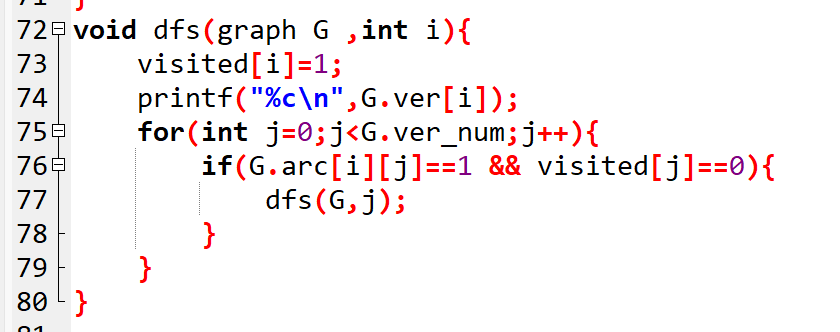
2. DFS 核心函数：侦探的行动指南

void dfs(graph G ,int i){

visited[i]=1; // 标记：这个人已经问过了

printf("%c\n",G.ver[i]); // 告诉老板：我找到他了

// 看看这个人认识的人里，有没有没问过的

for(int j=0;j.ver_num;j++){

// 条件：认识（arc[i][j]=1）且没问过（visited[j]=0）

if(G.arc[i][j]==1 && visited[j]==0){

dfs(G,j); // 冲！去下一家

}

}

}

这段代码翻译成人话就是：

• 到了第 i 个朋友家，先在本子上打勾（visited [i]=1），然后喊一声 “我到这儿了”（printf）；

• 挨个问这个朋友：“你认识的人里，谁还没被我问过？”；

• 只要找到一个没问过的，立刻冲过去（递归调用 dfs），把当前朋友扔在脑后；

• 等把这个朋友的所有 “关系链” 都问完，再回头找之前没走完的分支。

3. 实际运行效果（从 A 出发）

按照代码里的图结构，DFS 的走访顺序是：

A → B → C → D → E → F → G → H → I

（当然，顺序可能因循环顺序略有差异，但核心是 “一条路走到头”）

比如从 A 到 B，B 到 C，C 到 D，D 到 E，E 到 F（E 的朋友 F 没问过），F 到 G（F 的朋友 G 没问过），G 到 H（G 的朋友 H 没问过），H 的朋友都问过了，回头看 D 的朋友 I 没问过，最后去 I—— 完美遍历所有节点！

四、豁然开朗时刻：DFS 的核心是 “递归 + 回溯”

很多人觉得 DFS 难，其实就俩关键词：

• 递归：走得动就一直往下走（比如 A→B→C→D…）；

• 回溯：走不动了就回头找下一个分支（比如 H 没朋友了，回头找 D 的 I）。

就像你玩迷宫，遇到岔路先选左边，走到死胡同就退回来选右边，本质上和 DFS 是一个逻辑！而代码里的递归，就是帮我们自动 “退回来” 的魔法 —— 不用手动记录退路，函数调用栈会帮你搞定。

五、最后叨叨：DFS 有啥用？

别以为这只是个 “走访朋友” 的算法，实际用处可大了：

• 迷宫求解（找出口）；

• 搜索引擎爬虫（顺着链接爬网页）；

• 电路设计（找连通的元件）；

• 甚至游戏里的 “寻路 AI”（比如怪物追你时，找最短路径）。

而你给的代码，就是 DFS 最经典的实现 —— 用邻接矩阵存图，递归实现遍历，简单又直观，新手入门必看！