C：求一元二次方程ax^2+bx+c=0的根

分析

输入系数 a、b、c，用空格分隔。

如果 a=0 则是一元一次方程，根为 - c / b 。

a≠0 时，计算判别式，并根据三种情况用公式求根，结果保留两位小数。

另外用一个 ex 变量接受 sacnf() 返回值，如果 ex==3 则说明正确读取了3个数字，否则重新输入。

代码

#include <stdio.h>
#include <math.h>

int main()
{
	float x1 = 0, x2 = 0, d = 0, a = 0, b = 0, c = 0;
	int ch = 0, ex = 0; //ex用于根据scanf返回值判断输入是不是三个数字
	while (1)			//循环输入
	{
		printf("输入a(≠0) b c；Ctrl+C退出\n");
		ex = scanf("%f %f %f", &a, &b, &c);
		while ((ch = getchar()) != EOF && ch != '\n')
			; //吸收回车防止干扰
		if (ex != 3)
			printf("NO\n");
		else if (ex == 3) //ex=3说明正确读取了三个数字
		{
			if (a != 0)
			{
				d = b*b - 4*a*c;
				if (d > 0)
				{
					x1 = (-b + sqrt(d)) / (2 * a); //求根公式
					x2 = (-b - sqrt(d)) / (2 * a);
					printf("Δ = %.2f >0\nx1=%.2f\nx2=%.2f\n\n", d, x1, x2);
				} //保留两位小数
				else if (d == 0)//两相等实根
					printf("Δ = 0\nx1=x2=%.2f\n\n", -b / (2 * a));
				else//两个共轭复根
				{
					x1 = -b / (2 * a);
					x2 = (sqrt(-d)) / (2 * a);
					printf("Δ = %.2f <0\nx1=%.2f+i%.2f\n", d, x1, x2);
					printf("x2=%.2f-i%.2f\n\n", x1, x2);
				}
			}
			else
			{
				printf("a不能为0\n");
				printf("一次方程的根x=%.2f\n\n", -(c / b));
			}
		}
	}
	return 0;
}

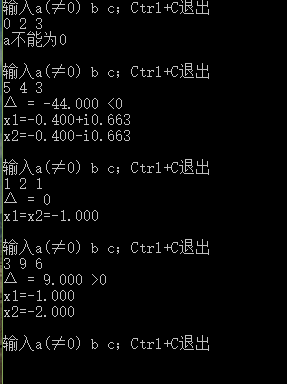
结果