题意:给你一棵树,每个节点有个value,定义一条路径的从u1开始到um的A(u1,um)为:
#include<stdio.h>
#include<vector>
#define mod 1000000007
using namespace std;
typedef long long ll;
vector<ll>vt[200005];
ll v[200005],dp[200005][2],num[200005][2],ans;
void dfs(ll u,ll fa)
{
ll now=0;
for(ll i=0;i<vt[u].size();i++)
{
ll to=vt[u][i];
if(to==fa)continue;
dfs(to,u);
dp[u][0]=((dp[u][0]+dp[to][1]-num[to][1]*v[u]%mod)%mod+mod)%mod;
dp[u][1]=((dp[u][1]+dp[to][0]+num[to][0]*v[u]%mod)%mod+mod)%mod;
num[u][0]=(num[u][0]+num[to][1])%mod;
num[u][1]=(num[u][1]+num[to][0])%mod;
}
for(ll i=0;i<vt[u].size();i++)
{
ll to=vt[u][i];
if(to==fa)continue;
if(num[to][0]!=0)now=((now+2*dp[to][0]*(num[u][1]-num[to][0])%mod+num[to][0]*(num[u][1]-num[to][0])*v[u]%mod)%mod+mod)%mod;
if(num[to][1]!=0)now=((now+2*dp[to][1]*(num[u][0]-num[to][1])%mod-num[to][1]*(num[u][0]-num[to][1])*v[u]%mod)%mod+mod)%mod;
}
now=((now+dp[u][1]*2+v[u])%mod+mod)%mod;
ans=(ans+now)%mod;
dp[u][1]=((dp[u][1]+v[u])%mod+mod)%mod;
num[u][1]=(num[u][1]+1)%mod;
}
int main()
{
ll n;
scanf("%lld",&n);
for(ll i=1;i<=n;i++)
scanf("%lld",&v[i]);
for(ll i=0;i<n-1;i++)
{
ll u,v;
scanf("%lld%lld",&u,&v);
vt[u].push_back(v);
vt[v].push_back(u);
}
dfs(1,1);
printf("%lld\n",ans%mod);
}
求所有路径的A(u1,um)的总和。
题解:当路径的长度是偶数时,这条路从开始走到结尾,与其从结尾走到开始的贡献为0,所以我们只需要考虑奇数长度的路径,定义dp[u][2]表示当前节点子树中往上到当前节点i的长度为偶数的路的A(vuj,vui)的和,num[u][2]表示从子树往上到当前节点i奇数长度的路径与偶数长度的路径的个数。根据当前节点的dp值,我们可以知道一条通过当前节点的有效路径肯定是两边长度的奇偶性是一样的,于是只要统计出答案即可。
AC代码:







 本文介绍了一种使用树形动态规划解决特定路径问题的方法,该问题要求计算一棵树上所有奇数长度路径的累加值。通过定义状态转移方程,文章详细解释了如何递归地计算每个节点的贡献值。
本文介绍了一种使用树形动态规划解决特定路径问题的方法,该问题要求计算一棵树上所有奇数长度路径的累加值。通过定义状态转移方程,文章详细解释了如何递归地计算每个节点的贡献值。
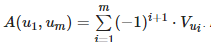
















 589
589

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








