差分约束系统之Bellman_Ford与Spfa判断负权回路

题目：http://poj.org/problem?id=1364

题意：就是简单的差分约束模型。

分析：首先我们必须知道，如果图中存在负权回路，那么差分约束没有可行解。而存在负权回路的条件是：图中某条边的松

弛操作的次数超过n次。对于Bellman_Ford，我们很容易解。如下：

#include <iostream>
#include <string.h>
#include <stdio.h>

using namespace std;
const int N = 105;
const int INF = 1<<29;

struct Edge
{
    int s,t;
    int w;
};

Edge edge[N*N];

int dist[N];
int cnt,n,m;

void add(int u,int v,int w)
{
    edge[cnt].s = u;
    edge[cnt].t = v;
    edge[cnt].w = w;
    cnt++;
}

void Relax(int s,int t,int w)
{
    if(dist[t] > dist[s] + w)
        dist[t] = dist[s] + w;
}

bool Bellman_Ford(int s)
{
    for(int i=0; i<n; i++)
        dist[i] = INF;
    dist[s] = 0;
    for(int i=0; i<n; i++)
        for(int j=0; j<cnt; j++)
            Relax(edge[j].s,edge[j].t,edge[j].w);
    for(int i=0; i<cnt; i++)
        if(dist[edge[i].t] > dist[edge[i].s] + edge[i].w)
            return true;
    return false;
}

int main()
{
    char str[5];
    while(cin>>n)
    {
        if(n == 0)  break;
        cin>>m;
        cnt = 0;
        while(m--)
        {
            int a,b,c;
            cin>>a>>b>>str>>c;
            if(str[0]=='l')
                add(a-1,a+b,c-1);
            else
                add(a+b,a-1,-c-1);
        }
        if(Bellman_Ford(0))  cout<<"successful conspiracy"<<endl;
        else                 cout<<"lamentable kingdom"<<endl;
    }
    return 0;
}

Bellman_Ford算法的时间复杂度为O(VE)，算法简单，适用范围又广，虽然复杂度稍高，仍不失为一个很实用的算法。

对于判断负权回路问题，我们还是用Spfa算法最好，时间复杂度比较低。实际上Spfa跟Bellman_Ford算法差不多，Spfa

是Bellman_Ford算法的一种队列实现，大大减少了不必要的冗余计算。

下面是Spfa判断负权回路的方法：

#include <iostream>
#include <string.h>
#include <stdio.h>
#include <queue>

using namespace std;
const int N = 105;
const int INF = 1<<29;

struct Edge
{
    int to;
    int w;
    int next;
};

Edge edge[N*N];

bool vis[N];
int head[N],time[N],dist[N];

int n,m,cnt;
queue<int> Q;

void add(int u,int v,int w)
{
    edge[cnt].to = v;
    edge[cnt].w = w;
    edge[cnt].next = head[u];
    head[u] = cnt++;
}

void Init()
{
    cnt = 0;
    memset(head,-1,sizeof(head));
    memset(vis,0,sizeof(vis));
    memset(time,0,sizeof(time));
}

bool Spfa(int s)
{
    for(int i=0; i<=n+1; i++)
        dist[i] = -INF;
    dist[s] = 0;
    time[s] = 1;
    vis[s] = 1;
    while(!Q.empty()) Q.pop();
    Q.push(s);
    while(!Q.empty())
    {
        int u  =Q.front();
        vis[u] = 0;
        Q.pop();
        for(int i=head[u]; ~i; i=edge[i].next)
        {
            int v = edge[i].to;
            int w = edge[i].w;
            if(dist[v] < dist[u] + w)
            {
                dist[v] = dist[u] + w;
                if(!vis[v])
                {
                    vis[v] = 1;
                    Q.push(v);
                    time[v]++;
                    if(time[v] > n)
                        return false;
                }
            }
        }
    }
    return true;
}

int main()
{
    char str[5];
    while(cin>>n)
    {
        Init();
        if(n == 0) break;
        cin>>m;
        for(int i=0; i<n+1; i++)
            add(0,i,0);
        while(m--)
        {
            int a,b,c;
            cin>>a>>b>>str>>c;
            if(str[0] == 'g')
                add(a + b + 1,a,c + 1);
            else
                add(a,a + b + 1,1 - c);
        }
        int s = 0;
        if(Spfa(s)) cout<<"lamentable kingdom"<<endl;
        else        cout<<"successful conspiracy"<<endl;
    }
    return 0;
}

当然，对于Spfa判负环，实际上还有优化：就是把判断单个点的入队次数大于n改为：如果总的点入队次数大于所有点两倍

时有负环，或者单个点的入队次数大于sqrt(点数)有负环。这样时间复杂度就降了很多了。

经典题目：

题目：http://acm.hdu.edu.cn/showproblem.php?pid=3666

分析：本题要先取对数，然后转化为差分约束模型，再判断有没有解就可以了。注意这里时间限制紧，判负环要优化。

题目：http://poj.org/problem?id=3259

分析：典型的差分约束题目，直接判断负环就行，这里数据不大，可以直接就用单个点入队次数是否超过n判断就可以了。

题目：http://acm.hdu.edu.cn/showproblem.php?pid=1384

题意：在每个区间上至少选择个元素，构成一个集合S，使得集合S中的元素最少。

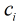
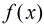
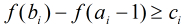
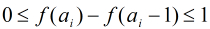
分析：设表示在区间上选择的元素的个数。那么有：，并且很明显还有：

，然后我们根据这两个不等式建图，然后就转化为最长路径问题。

#include <iostream>
#include <string.h>
#include <stdio.h>
#include <queue>

using namespace std;
const int N = 50005;
const int INF = 1<<30;

struct Edge
{
    int to;
    int w;
    int next;
};

Edge edge[4*N];

bool vis[N];
int head[N],dist[N];
int cnt,s,t;

queue<int> Q;

void Init()
{
    cnt = 0;
    memset(vis,0,sizeof(vis));
    memset(head,-1,sizeof(head));
}

void add(int u,int v,int w)
{
    edge[cnt].to = v;
    edge[cnt].w = w;
    edge[cnt].next = head[u];
    head[u] = cnt++;
}

void Spfa(int s)
{
    for(int i=0; i<N; i++)
        dist[i] = -INF;
    dist[s] = 0;
    while(!Q.empty()) Q.pop();
    Q.push(s);
    vis[s] = 1;
    while(!Q.empty())
    {
        int u = Q.front();
        vis[u] = 0;
        Q.pop();
        for(int i=head[u]; ~i; i=edge[i].next)
        {
            int v = edge[i].to;
            int w = edge[i].w;
            if(dist[v] < dist[u] + w)
            {
                dist[v] = dist[u] + w;
                if(!vis[v])
                {
                    vis[v] = 1;
                    Q.push(v);
                }
            }
        }
    }
}

int main()
{
    int n;
    while(~scanf("%d",&n))
    {
        Init();
        s = INF;
        t = -1;
        while(n--)
        {
            int u,v,w;
            scanf("%d%d%d",&u,&v,&w);
            if(u < s)  s = u;
            if(v + 1 > t) t = v + 1;
            add(u,v+1,w);
        }
        for(int i=s; i<=t; i++)
        {
            add(i,i-1,-1);
            add(i-1,i,0);
        }
        Spfa(s);
        printf("%d\n",dist[t]);
    }
    return 0;
}