量子计算：从入门到进阶

置顶莲华君

已于 2025-04-19 18:55:52 修改

阅读量1.1k

点赞数 36

文章标签：量子计算

于 2025-04-18 13:58:25 首次发布

本文链接：https://blog.csdn.net/Aria_Miazzy/article/details/147328217

版权

《量子计算：从入门到进阶》

——从量子叠加到现实颠覆的认知跃迁

引言：当硬币旋转时，世界开始改变

从经典到量子：一个不可思议的旅程

想象一下，你正站在一个巨大的迷宫入口，面前是无数条错综复杂的路径。在经典计算的世界里，计算机就像一个勤奋但有点“死脑筋”的探险家，它只能一次尝试一条路径，缓慢而坚定地寻找出口。而你，作为旁观者，只能耐心等待，希望它最终能找到正确的路。

但现在，请想象另一种可能性：在这个迷宫中，你拥有一种神奇的力量，可以同时探索所有路径，仿佛你拥有无数个分身，每个分身都沿着不同的路径前进。这就是量子计算的世界，一个充满奇迹和无限可能的领域。

1. 硬币的启示：当“非此即彼”成为过去式

想象一枚永远旋转的硬币——在它停下的瞬间，你只能看到“正面”或“反面”，正如经典计算机的比特非0即1。但若在硬币旋转时窥探它的秘密，你会发现一种颠覆认知的真相：它同时是正与反的叠加态。这便是量子比特的魔力——一种既能包容矛盾，又因“观测”而坍缩为确定性的存在。

关键隐喻：量子世界像一场未落幕的戏剧，所有可能性同时上演，直到观众入场才选定结局。

2. 幽灵契约：跨越时空的量子纠缠

若将两枚硬币用“量子魔法”绑定，即便相隔银河，它们也会默契地呈现相反状态。爱因斯坦曾称此为“幽灵般的超距作用”，而今日的科学家正用这种量子纠缠构建新型计算语言——两个量子比特的关联无需任何信号传递，却能实现超越经典极限的信息同步。

冷知识：量子纠缠虽能“瞬间感应”，却无法传递有效信息（物理法则依旧捍卫着光速不可逾越的铁律）。

3. 魔法手套：量子门的概率之舞

经典计算机用逻辑门（如AND/OR）像木匠般精确凿刻0与1；量子计算机的“量子门”却像巫师的手套，扭曲概率波的形态，让叠加态中的无数可能性同时演化。例如，它能让一台量子计算机在眨眼间尝试所有密码组合——就像让一支军队同时探索迷宫的每一条岔路。

震撼案例：Shor算法利用这一特性，理论上可瓦解现代银行系统的RSA加密堡垒（前提是量子比特足够多且稳定）。

4. 脆弱的神迹：量子世界的蝴蝶效应

量子态如同晨露上的肥皂泡，温度波动、电磁干扰甚至一次不经意的观测，都可能引发退相干——量子信息如泡沫般破裂消散。为此，科学家发明了“量子纠错码”：用数百个物理量子比特保护一个逻辑比特，如同为易碎的水晶打造钢铁盔甲。

现实挑战：今天的量子计算机像初生婴孩，需在-273℃的超低温中运行，且错误率居高不下。

5. 未来已来：计算的维度革命

量子计算绝非“更快”的经典计算机，而是一场计算本质的范式革命：

药物设计：模拟分子量子行为，加速癌症药物研发
物流优化：为全球航运网络找到最优路径
人工智能：重构机器学习底层逻辑

当前量子技术相当于1940年代的电子管计算机，但其发展速度远超摩尔定律。正如蒸汽机开启了工业文明，量子计算或许正孕育着下一次文明级跃迁的种子。

本书将带你完成的旅程：

从旋转硬币的比喻走向希尔伯特空间的数学之美
从量子幽灵的玄妙触及超导量子芯片的工程细节
从实验室的低温装置眺望量子互联网的星际蓝图

翻开下一页，你将不再是被动的观察者，而是量子革命的共舞者——在这里，矛盾即是力量，不确定孕育可能，而每一个量子比特的旋转，都在重构人类认知的边界。

导言：量子计算的寒武纪大爆发

从图灵机到量子比特：计算范式的维度跃迁
历史三幕剧：薛定谔的猫→贝尔不等式→量子霸权
认知框架："物理直觉×数学语言×工程实践"三维穿透法

量子计算的寒武纪大爆发

翻开这本书，你将解锁人类史上最炸裂的科技革命！

准备好了吗？我们即将穿越到量子世界，见证一场比寒武纪生命大爆发更震撼的算力狂飙！这可不是普通的技术升级，而是一场要掀翻传统计算机桌子的颠覆风暴——你的手机、电脑甚至超级计算机，在它面前都会秒变"古董算盘"！

寒武纪2.0已启动：量子计算，一场算力革命正在改写人类文明！

还记得5亿年前那个生命大爆炸的奇迹吗？现在的量子计算界正在上演同样疯狂的进化！全球实验室里，科学家们像造物主一样"捏"出各种量子黑科技，这场景就像当年三叶虫突然进化成霸王龙一样刺激！

💥 量子三件套颠覆世界：

叠加态暴走：量子比特同时狂飙亿万种可能，传统计算机还在吭哧吭哧跑单线程

纠缠术开挂：隔着一个银河系也能"心电感应"，数据传输直接突破光速结界

量子干涉秀：在亿万可能性中精准锁定正确答案，就像给大海捞针装上了GPS

为什么说这是改变游戏规则的时刻？

最近三年爆发的黑科技：

谷歌量子计算机3分20秒干完超算1万年的活
中国科学家把量子纠缠传送到1200公里外
微软搞出能自我纠错的"不死量子比特"

现实世界已沦陷：

银行金库正在连夜更换量子加密锁
制药巨头用量子计算机设计"长生药"
马斯克团队悄悄研发量子版自动驾驶
天气预报即将精确到分钟级！

暗流涌动：

当量子计算机能暴力破解所有密码，当某个国家垄断量子霸权，当AI装上量子引擎...这场革命带来的不仅是机遇，更是全人类必须面对的生存级挑战！

这本书能给你什么超能力？
✔️ 量子黑话翻译器：从"叠加态"到"拓扑量子"，让你三句话唬住投资人
✔️ 未来商业藏宝图：提前锁定量子计算+金融/医药/AI的万亿级风口
✔️ 人类文明生存指南：在量子时代如何守住你的财富、隐私和安全

这不是一本教科书，而是一张通往未来的船票。当量子计算撕开时空裂缝时，你可以选择继续围观——或者，跟着我们纵身跃入这个算力沸腾的新纪元！

从图灵机到量子比特：计算范式的维度跃迁

当传统计算机还在二进制小路上蹬三轮，量子比特已经开着曲速引擎冲进星辰大海！让我们一起回顾计算机的算力进化史吧！

图灵机：计算机的"老祖宗"长啥样？

1936年某个阴雨的英国下午
数学怪才图灵在咖啡馆画下改变世界的草图——

无限纸带+机械头：这台想象中的机器，居然藏着所有电脑的灵魂！你的手机、笔记本甚至超算，都是它的曾曾曾孙

天才洞察：只要能用算法描述的问题，这台机器都能解！但有个致命bug...

图灵魔咒：所有传统计算机都被封印在这个模型里，就像恐龙永远飞不上蓝天

经典计算机的末日审判

当AI、元宇宙、核聚变都在喊"饿"——

传统计算机突然发现自己得了绝症：

指数级龟速：要破解银行密码？等地球爆炸吧！要模拟新药分子？太阳熄灭都算不完！
量子模拟灾难：30个量子比特的运算，能把全球硬盘撑爆！科学家怒吼：我们需要算力核弹！
神秘预言：摩尔定律将死，硅基芯片已触天花板...除非找到新次元入口！

量子比特：来自高维空间的作弊器

物理学家的逆袭：既然打不过，就修改物理规则！

他们从量子世界偷来三大神器：

1️⃣ 分身叠加态：一个量子比特=∞个经典比特同时运算
2️⃣ 纠缠感应术：隔银河系也能瞬间同步，算力直接突破三维限制
3️⃣ 量子干涉术：在亿万可能性中精准捞出答案，就像拥有预知未来的水晶球

震惊案例：

传统超算要算10万年的药物分子，量子计算机分分钟就能搞定
比特币加密在量子算法面前像纸糊的，金融圈连夜研发量子盾牌
AI喂了量子算力后，突然顿悟般跨入新次元...

维度战争：当算力突破物理法则

这不是升级，是降维打击！

操作模式：从"开/关"的二极管思维，到驾驭概率云的量子冲浪
数学革命：希尔伯特空间取代二进制，每个方程都在扭曲现实
新宇宙法则：量子纠缠无视光速，并行计算撕裂时空连续性

未来已来：你准备好被量子化了吗？

职业地震：密码学家下岗？材料科学家转行？金融交易员失业？
生存挑战：当量子计算机能模拟宇宙大爆炸，我们该如何控制这种神力？
人类2.0：脑机接口+量子AI=？或许意识上传就在下个十年...

历史三幕剧：薛定谔的猫→贝尔不等式→量子霸权

欢迎继续深入量子计算的探索之旅。在本节中，我们将通过历史三幕剧的形式，回顾量子计算发展历程中的三个关键时刻。这些关键时刻不仅塑造了量子力学的基础理论，还推动了量子计算从理论走向实践，最终实现了量子霸权的里程碑。让我们一同回顾这段波澜壮阔的历史旅程。

第一幕：薛定谔的猫 —— 量子力学的奇异世界

1. 背景：量子力学的诞生

20世纪初： 量子力学作为一门新兴学科诞生，颠覆了经典物理学对微观世界的理解。
核心概念： 叠加性、不确定性原理、量子态的波函数描述等。

2. 薛定谔的猫思想实验

提出者： 奥地利物理学家埃尔温·薛定谔在1935年提出了这个著名的思想实验。
实验描述：
- 一只猫被关在一个密闭的盒子里，盒子里有一个放射性原子、一个盖革计数器、一瓶毒药和一个装置。
- 如果放射性原子发生衰变，盖革计数器会检测到，并触发装置释放毒药，导致猫死亡。
- 根据量子力学的叠加原理，在未进行观测之前，放射性原子处于衰变和未衰变的叠加态。
- 因此，猫也处于“既死又活”的叠加态。

3. 思想实验的意义

量子叠加性： 薛定谔的猫生动地展示了量子叠加性的奇异特性，即微观粒子可以同时处于多个状态。
测量问题： 思想实验引发了关于量子测量问题的讨论，即观测如何导致量子态的坍缩。
量子力学的解释： 薛定谔的猫成为不同量子力学解释（例如，哥本哈根解释、多世界解释）争论的焦点。

4. 对量子计算的影响

量子态的操控： 薛定谔的猫启发了科学家们思考如何操控和利用量子叠加态进行计算。
量子比特的诞生： 量子比特的概念正是基于量子叠加性，它能够同时表示 0 和 1 的叠加态。

第二幕：贝尔不等式 —— 量子纠缠的胜利

1. 背景：爱因斯坦-波多尔斯基-罗森佯谬（EPR 佯谬）

1935年： 爱因斯坦、波多尔斯基和罗森发表论文，对量子力学的完备性提出质疑。
核心问题： 量子纠缠现象似乎违反了经典物理学的局域性原理，即“鬼魅般的超距作用”。

2. 贝尔不等式的提出

约翰·贝尔（John Bell）： 1964年，贝尔提出了一个不等式，为检验量子纠缠的真实性提供了实验依据。
贝尔不等式： 描述了经典局域性理论对某些测量结果的限制。

3. 阿斯派克特实验

阿兰·阿斯派克特（Alain Aspect）： 1982年，阿斯派克特等人进行了著名的实验，验证了贝尔不等式被违反。
实验结果： 实验结果表明，量子纠缠是真实存在的，量子力学对微观世界的描述是准确的。

4. 对量子计算的影响

量子纠缠的确认： 贝尔不等式的验证证实了量子纠缠的存在，为量子计算奠定了理论基础。
量子通信的基础： 量子纠缠是量子密钥分发和量子隐形传态等量子通信技术的基础。
量子计算的资源： 量子纠缠是量子计算的重要资源，可以实现量子并行计算和量子纠缠态的操作。

第三幕：量子霸权 —— 量子计算的里程碑

1. 背景：量子计算的发展

20世纪90年代以来： 量子计算理论不断发展，量子算法（例如，Shor 算法、Grover 算法）被提出。
量子硬件的进步： 超导量子计算、离子阱量子计算、光子量子计算等技术取得突破。

2. 谷歌的量子霸权实验

2019年10月： 谷歌的研究团队在《Nature》杂志上发表论文，声称其量子处理器“悬铃木”（Sycamore）实现了量子霸权。
实验内容： 悬铃木处理器包含53个量子比特，在200秒内完成了一项复杂的随机量子电路采样任务，而谷歌估计，使用目前最强大的超级计算机完成同样的任务需要1万年。

3. 量子霸权的意义

计算能力的证明： 量子霸权的实现证明了量子计算在某些特定任务上具有超越经典计算的能力。
技术突破的标志： 量子霸权的实现标志着量子计算技术取得了重大突破，激励着科学家们继续探索量子计算的应用。
挑战与争议： 量子霸权的实现也引发了关于其实际意义的讨论，例如，量子霸权任务是否具有实际应用价值，以及量子计算机是否能够解决实际问题。

4. 对量子计算的影响

推动技术进步： 量子霸权的实现激励着研究人员开发更强大的量子硬件和更高效的量子算法。
加速商业化进程： 量子霸权的实现吸引了更多企业和机构投资量子计算，加速了量子计算的商业化进程。
引发社会关注： 量子霸权的实现引发了公众对量子计算的广泛关注，促进了量子计算知识的普及。

通过回顾量子计算发展历程中的三个关键时刻，我们可以更好地理解量子计算的发展脉络：

薛定谔的猫： 揭示了量子力学的奇异特性，为量子计算提供了理论基础。
贝尔不等式： 证实了量子纠缠的存在，为量子通信和量子计算奠定了基础。
谷歌量子霸权： 标志着量子计算技术取得了重大突破，激励着量子计算的未来发展。

这些关键时刻不仅塑造了量子计算的历史进程，还为我们描绘了一幅充满希望的未来图景。

认知框架："物理直觉×数学语言×工程实践"三维穿透法

欢迎继续深入量子计算的探索之旅。在前面的内容中，我们探讨了从图灵机到量子比特的演变，以及量子计算发展历程中的三个关键时刻。在本节中，我们将介绍本书的认知框架："物理直觉×数学语言×工程实践"三维穿透法。这一框架旨在帮助读者从多个维度全面理解量子计算的本质和应用。接下来，我们将详细解释每个维度，并说明它们如何协同作用，以实现对量子计算的深入理解。

一、物理直觉：理解量子世界的本质

1. 什么是物理直觉？

物理直觉： 指对物理现象和原理的直观理解和感知。它不仅仅是记住公式和定理，而是能够从物理世界的本质出发，理解和解释各种现象。

2. 量子力学的核心概念

叠加性： 量子比特可以同时处于多个状态，例如，。这种特性是量子计算强大计算能力的基础。
- 类比： 就像一个旋转的硬币，在落地之前，它同时处于正面和反面的叠加状态。
纠缠性： 两个或多个量子比特可以形成纠缠态，即使它们相距遥远，一个量子比特的状态变化会立即影响另一个量子比特的状态。
- 类比： 就像一对双胞胎，无论相隔多远，一个人的情绪变化会立即影响另一个人。
不确定性原理： 对某些物理量（例如，位置和动量）的同时测量存在基本限制。
- 类比： 就像试图同时测量一个高速旋转的陀螺的位置和速度，测量一个会影响另一个。
量子干涉： 量子态之间可以发生干涉，从而影响计算结果。
- 类比： 就像水波相互叠加，可以产生增强或抵消的效果。

3. 物理直觉的重要性

理解量子现象： 物理直觉帮助我们理解量子力学的奇异特性，例如，叠加性、纠缠性和不确定性原理。
设计量子算法： 物理直觉可以帮助我们设计更有效的量子算法，例如，利用量子干涉来增强正确结果的概率。
解决实际问题： 物理直觉可以帮助我们将量子计算应用于实际问题，例如，模拟量子系统、优化问题等。

二、数学语言：描述量子世界的工具

1. 什么是数学语言？

数学语言： 指用数学符号、公式和逻辑推理来描述和解释物理现象。它为量子力学和量子计算提供了精确的描述和严谨的理论基础。

2. 量子力学的数学基础

希尔伯特空间： 量子态空间被表示为希尔伯特空间，量子比特的状态可以用复向量来表示。
- 公式： ，其中 α 和 β 是复数，满足。
算符： 量子力学中的物理量（例如，能量、动量）由厄米算符表示。
薛定谔方程： 描述量子态随时间的演化。
- 公式：，其中是哈密顿算符。

3. 量子计算的数学描述

量子门： 量子门是量子计算的基本操作单元，可以用幺正矩阵来表示。
- 例子： Hadamard 门、CNOT 门、Pauli 门等。
量子电路： 量子电路由一系列量子门组成，可以用矩阵乘法来描述其操作。
量子算法： 量子算法可以用量子电路来表示，并通过量子力学原理来分析其性能。

4. 数学语言的重要性

精确描述： 数学语言为量子力学和量子计算提供了精确的描述，避免了模糊和歧义。
理论分析： 数学工具（例如，线性代数、概率论）可以帮助我们分析量子系统的行为和量子算法的性能。
设计优化： 数学语言可以帮助我们优化量子电路的设计，提高量子计算的效率。

三、工程实践：实现量子计算的关键

1. 什么是工程实践？

工程实践： 指将理论和技术转化为实际应用的过程。在量子计算领域，工程实践涉及量子硬件的制造、量子控制系统的开发、量子软件的实现等。

2. 量子硬件的实现

量子比特的实现： 不同的物理系统被用于实现量子比特，例如，超导量子比特、离子阱量子比特、光子量子比特等。
量子门操作： 量子门操作需要精确的控制和测量技术，以确保量子计算的准确性。
量子纠错： 为了克服量子退相干和量子错误，需要实现量子纠错码，例如，表面编码、拓扑量子纠错等。

3. 量子控制与测量

量子控制： 精确控制量子比特的量子态是实现量子计算的关键，需要开发先进的控制技术，例如，微波控制、激光控制等。
量子测量： 量子测量需要高精度的测量设备和技术，以获取量子态的信息。

4. 量子软件开发

量子编程框架： 开发功能强大、易于使用的量子编程框架和工具，例如，Qiskit、Cirq、Q# 等。
量子编译器： 将高级量子算法编译成可执行的量子电路，并进行优化。
量子模拟器： 模拟量子算法的行为，帮助开发者进行调试和优化。

5. 工程实践的重要性

实现理论： 工程实践将量子力学的理论转化为实际的量子计算系统。
推动技术进步： 工程实践中的挑战和突破推动着量子计算技术的发展。
应用落地： 工程实践使得量子计算的应用成为可能，例如，量子化学模拟、量子机器学习等。

四、三维协同：构建完整的量子计算认知体系

1. 物理直觉、数学语言和工程实践的协同作用

相互促进： 物理直觉为数学语言和工程实践提供方向和灵感；数学语言为物理直觉和工程实践提供精确描述和理论支持；工程实践为物理直觉和数学语言提供验证和应用场景。
循环迭代： 三者之间形成了一个循环迭代的过程，推动着量子计算的发展。例如，物理直觉激发新的量子算法设计，数学语言分析其性能，工程实践实现其应用，并反馈新的物理直觉。

2. 全面理解量子计算

多维度视角： 通过物理直觉、数学语言和工程实践三个维度，我们可以从多个角度全面理解量子计算的本质和应用。
深入浅出： 这种三维穿透法可以帮助读者在理解量子计算的基本概念的同时，也能深入了解其背后的物理原理和工程实现。
应用导向： 这种方法强调了量子计算的实际应用价值，引导读者思考如何将量子计算技术应用于实际问题。

在本节中，我们介绍了本书的认知框架："物理直觉×数学语言×工程实践"三维穿透法：

物理直觉： 帮助我们理解量子世界的本质，例如，叠加性、纠缠性和不确定性原理。
数学语言： 为我们提供了描述量子现象和量子计算的工具，例如，希尔伯特空间、量子门和量子电路。
工程实践： 实现了量子计算从理论到实践的跨越，例如，量子硬件、量子控制、量子软件等。

本书将通过三维协同的方式：即物理直觉、数学语言和工程实践三者相互促进，共同构建了完整的量子计算认知体系。通过运用这一认知框架，您可以更全面、更深入地理解量子计算，并为其未来的发展贡献力量。

现在，请让我们一起按下量子阅读的启动键——3...2...1...穿越开始！

！@#￥￥#￥…*&%￥…&*￥%……&*

》》时空漩涡

》》欢迎来到量子计算的法则世界！

第一部分：量子世界基础篇

第1章量子力学第一性原理

叠加态与坍缩：双缝实验的哲学启示
量子纠缠之谜：EPR佯谬与贝尔态的非定域性
不可克隆定理：量子信息学的保护神

1.1 叠加态与坍缩：双缝实验的哲学启示

亲爱的读者，欢迎来到量子力学的奇妙世界。在本章中，我们将深入探讨量子力学中最具代表性的实验之一——双缝实验，以及它所揭示的叠加态与坍缩概念。这些概念不仅是量子力学的核心支柱，更蕴含着深刻的哲学启示，挑战着我们对于现实本质的认知。为了让这段旅程既富有深度又充满趣味，我们将从多个角度展开讨论，包括实验背景、历史发展、理论分析、哲学思考以及其在现代科技中的应用。

一、双缝实验的起源与发展：从经典到量子的跨越

1.1.1 经典双缝实验：光的波动性

双缝实验的历史可以追溯到19世纪初，由英国科学家托马斯·杨（Thomas Young）在1801年首次提出。这个实验最初是为了解决一个长期存在的争论：光是粒子还是波？

实验装置：

一个光源发射光线。
光线通过一个有两条缝隙的屏幕。
在屏幕后方放置一个观察屏，用于记录光线的到达位置。

实验结果：

在观察屏上出现了明暗相间的条纹，即干涉图样。
这种干涉图样是波特有的现象，表明光具有波动性。

经典解释：

光被看作是一种波，通过双缝后分成两部分。
这两部分波在观察屏处重新叠加，形成干涉图样。

托马斯·杨的实验成功地证明了光的波动性，结束了关于光是粒子还是波的争论。然而，这个结论在20世纪初被量子力学的出现彻底颠覆。

1.1.2 量子双缝实验：光的粒子性

20世纪初，随着量子力学的兴起，科学家们开始重新审视双缝实验。1905年，爱因斯坦提出了光量子假说，认为光由离散的粒子（光子）组成。这一假说在1923年被康普顿散射实验所证实。

量子双缝实验的设置与经典实验类似，但光源被减弱到每次只发射一个光子。

实验结果：

单个光子通过双缝后，在观察屏上仍然形成了干涉图样。
这意味着单个光子似乎同时通过了双缝，并与自身发生了干涉。

解释：

光子被描述为一个波函数，这个波函数在通过双缝时分裂成两部分。
这两部分波函数在观察屏处重新叠加，形成干涉图样。

这个结果令人震惊，因为它表明光子既具有粒子性，又具有波动性，即波粒二象性。单个光子似乎能够同时通过两条缝隙，这与经典物理学中的粒子概念完全相悖。

1.1.2.1 波粒二象性：量子力学的核心概念

波粒二象性是量子力学中最具革命性的概念之一。它表明，微观粒子（如电子、光子等）既可以表现为粒子，也可以表现为波，具体表现为哪种形式取决于实验设置。

粒子性： 粒子具有确定的位置和动量，可以被探测到。
波动性： 波具有干涉、衍射等特性，可以与自身发生干涉。

在双缝实验中，光子的波动性表现为干涉图样的形成，而其粒子性则表现为单个光子的探测。

1.1.2.2 量子力学的概率解释

量子力学对双缝实验的解释基于概率解释，即：

光子通过双缝的概率由波函数的平方决定，即。
波函数 ψ 描述了光子可能的状态。
测量结果是不确定的，服从量子力学的概率分布。

这种概率解释与经典物理学中的确定性描述截然不同。在经典物理学中，粒子的运动轨迹是确定的，可以被精确预测。而在量子力学中，我们只能预测粒子在某一位置出现的概率。

二、叠加态：量子世界的奇异本质

1.1.3 叠加态的概念

在量子力学中，叠加态是一个核心概念，指的是一个量子系统可以同时处于多个状态的叠加中。

1.1.3.1 数学描述

在量子力学中，量子态由波函数描述。波函数是一个复值函数，其平方的绝对值表示粒子在空间中出现的概率密度。

线性叠加原理： 量子态的叠加是线性的，即如果和是两个可能的量子态，那么它们的任意线性组合（其中 c1 和 c2 是复数）也是一个可能的量子态。
归一化条件： 波函数必须满足归一化条件，即，确保粒子在空间中出现的总概率为1。

在双缝实验中，单个光子的波函数可以表示为：

其中，ψ1 和 ψ2 分别表示光子通过缝隙1和缝隙2的状态。

1.1.3.2 物理意义

叠加态是量子力学与经典物理学最根本的区别之一。在经典物理学中，一个物体只能处于一个确定的状态。例如，一个硬币要么是正面朝上，要么是反面朝上，不可能同时处于两种状态的叠加中。

然而，在量子力学中，量子系统可以同时处于多个状态的叠加中。这种叠加态并不是一种简单的混合，而是量子系统的一种真实存在状态。例如，在双缝实验中，单个光子同时处于通过两条缝隙的状态，这种状态是真实的，而不是一种数学上的抽象。

1.1.3.3 奇异性质

干涉现象： 叠加态的存在是量子干涉现象的根源。在双缝实验中，单个光子与自身的波函数发生干涉，形成了干涉图样。
量子纠缠： 叠加态是量子纠缠的基础。两个或多个量子系统可以处于纠缠态，即它们的量子态是相互关联的，即使它们相距遥远。

1.1.3.4 量子叠加的实例

自旋叠加： 一个电子可以处于自旋向上和自旋向下的叠加态。
能量叠加： 一个原子可以处于不同能级的叠加态。
位置叠加： 一个粒子可以处于不同位置的叠加态。

1.1.3.5 量子叠加的应用

量子计算： 量子比特的叠加态是量子计算的基础，使得量子计算机能够并行处理大量信息。
量子通信： 量子纠缠态可以用于实现量子通信，实现信息的安全传输。
量子传感： 量子叠加态可以用于制造高精度的量子传感器，例如原子钟、量子磁力计等。

三、坍缩：从量子到经典的桥梁

1.1.4 坍缩的概念

坍缩是量子力学中另一个关键概念，指的是当对量子系统进行测量时，系统的波函数会突然从多个状态的叠加态“坍缩”到一个确定的状态。

在双缝实验中，当光子到达探测器时，其波函数从叠加态：

坍缩到一个确定的位置，例如：

1.1.4.1 坍缩的瞬时性和不可逆性

瞬时性： 坍缩过程是瞬时的，不存在任何过渡状态。
不可逆性： 坍缩过程是不可逆的，一旦发生，量子态就无法恢复到原来的叠加态。

1.1.4.2 哥本哈根解释

哥本哈根解释是量子力学最著名的解释之一，由尼尔斯·玻尔和维尔纳·海森堡提出。该解释认为：

量子系统的状态由波函数描述。
测量过程会导致波函数坍缩。
测量结果是不确定的，服从量子力学的概率解释。

然而，哥本哈根解释并没有解释坍缩的具体机制，也没有解释测量过程与普通物理过程之间的区别。

1.1.4.3 测量问题

测量问题是量子力学中最具挑战性的问题之一。它可以表述为：

为什么测量会导致波函数坍缩？
测量过程与普通物理过程有何不同？
量子力学的基本方程（薛定谔方程）是确定性的，但测量结果却是不确定的，如何解释这种矛盾？

1.1.4.4 量子坍缩的解释

哥本哈根解释： 强调测量过程的重要性，但无法解释坍缩机制。
多世界解释： 认为每次测量都会导致宇宙分裂成多个平行宇宙，每个宇宙对应于测量结果的一种可能性。
隐变量理论： 试图引入隐藏的变量来解释量子力学的概率性，但目前尚未得到实验证实。
量子退相干理论： 解释了量子系统如何与环境相互作用，导致量子相干性的丧失，从而解释了经典世界的出现。

1.1.4.5 量子退相干理论

量子退相干理论是解释量子坍缩的一种重要理论。该理论认为：

量子系统与环境的相互作用会导致量子相干性的丧失。
量子相干性的丧失使得量子系统表现出经典的行为。
测量过程可以被看作是一种特殊的量子退相干过程。

量子退相干理论为理解量子坍缩提供了一种新的思路，但它并没有完全解决测量问题。

四、哲学启示：挑战经典世界观

双缝实验及其背后的叠加态和坍缩概念，对经典世界观提出了严峻挑战，引发了深刻的哲学思考。

1.1.5.1 实在性问题

经典实在性： 在经典物理学中，物体的属性是客观存在的，不依赖于观测。
量子实在性： 在量子力学中，量子态的叠加性意味着物体的属性在测量之前并不确定，而是处于一种不确定的状态。

1.1.5.2 因果性问题

经典因果性： 在经典物理学中，事件的发生是由初始条件决定的，遵循严格的因果关系。
量子因果性： 在量子力学中，测量结果具有内在的随机性，不存在严格的因果关系。

1.1.5.3 观测者的角色

经典观测者： 在经典物理学中，观测者是被动的，不会影响被观测的对象。
量子观测者： 在量子力学中，观测者的存在和测量行为会影响量子系统的状态。

1.1.5.4 量子力学的解释问题

哥本哈根解释： 强调测量过程的重要性，但无法解释坍缩机制。
多世界解释： 认为每次测量都会导致宇宙分裂成多个平行宇宙，每个宇宙对应于测量结果的一种可能性。
隐变量理论： 试图引入隐藏的变量来解释量子力学的概率性，但目前尚未得到实验证实。
量子退相干理论： 解释了量子系统如何与环境相互作用，导致量子相干性的丧失，从而解释了经典世界的出现。

1.1.5.5 量子力学的哲学影响

对经典物理学的挑战： 量子力学打破了经典物理学中关于实在性、因果性、决定论等基本假设。
对哲学的影响： 量子力学引发了关于物质世界本质、意识与物质的关系、观测者的角色等哲学问题的深入思考。
对人类认知的影响： 量子力学改变了我们对宇宙的理解，揭示了微观世界的奇异性和复杂性。

五、量子计算：叠加态与坍缩的应用

双缝实验所揭示的叠加态和坍缩概念，不仅具有理论意义，还在现代科技中找到了应用，其中最引人注目的就是量子计算。

1.1.6.1 量子比特与叠加态

经典比特： 经典计算机的基本单位是比特，它只能处于0或1两种状态之一。
量子比特（qubit）： 量子计算机的基本单位是量子比特，它可以处于0和1的叠加态，即：

其中，α 和 β 是复数，满足。
量子叠加的优势： 量子比特的叠加态使得量子计算机能够同时处理大量信息，从而实现并行计算。

1.1.6.2 量子纠缠与量子门

量子纠缠： 量子比特之间可以处于纠缠态，即它们的量子态是相互关联的，即使它们相距遥远。
量子门： 量子门是量子计算的基本操作单元，它可以对量子比特进行操作，例如旋转、翻转等。
量子纠缠的应用： 量子纠缠可以用于实现量子门操作，从而实现量子计算。

1.1.6.3 量子坍缩与量子测量

量子测量： 在量子计算中，量子测量是必不可少的步骤，它将量子比特的叠加态坍缩到一个确定的状态。
量子测量的挑战： 量子测量会导致量子相干性的丧失，从而影响量子计算的准确性。
量子纠错： 为了克服量子测量的问题，量子计算机需要采用量子纠错技术来保护量子信息。

1.1.6.4 量子计算的应用前景

密码学： 量子计算可以破解许多现有的加密算法，例如RSA算法。
材料科学： 量子计算可以模拟复杂的量子系统，从而加速新材料的设计。
人工智能： 量子计算可以加速机器学习算法的训练，提高人工智能的性能。

1.1.6.5 量子计算面临的挑战

量子相干性： 量子相干性的丧失是量子计算面临的主要挑战之一。
量子纠错： 量子纠错技术是实现大规模量子计算的关键。
量子硬件： 制造稳定的、可扩展的量子硬件是量子计算发展的瓶颈。

六、结语

双缝实验是量子力学的象征，它揭示了量子世界的奇异本质，挑战了我们对于现实的理解。叠加态和坍缩概念不仅是量子力学的核心支柱，更蕴含着深刻的哲学启示。

通过深入探讨双缝实验，我们不仅能够更好地理解量子力学的原理，还能更深刻地思考一些根本性的哲学问题，例如：

什么是实在性？
因果关系是普遍存在的吗？
观测者的角色是什么？
量子力学的基本问题如何影响我们对宇宙的理解？

这些问题没有简单的答案，但正是这些问题的存在，推动着人类对宇宙奥秘的不断探索。

在量子计算领域，叠加态和坍缩概念为实现更强大的计算能力提供了新的思路。随着量子计算技术的不断发展，我们有理由相信，量子计算机将在未来改变我们的生活方式，推动科学技术的进步。

总而言之，双缝实验和量子力学为我们打开了一扇通往未知世界的大门，而探索这片神秘领域的过程，将继续激励着无数科学家和哲学家不断前行。

希望这段旅程能够激发您对量子力学的兴趣，并为您理解量子计算的未来发展提供一些启示。

1.2 量子纠缠之谜：EPR佯谬与贝尔态的非定域性

亲爱的读者，欢迎继续我们的量子力学探索之旅。在上一节中，我们探讨了叠加态与坍缩，以及它们在双缝实验中的体现，这些概念揭示了量子世界与经典物理学的根本区别。然而，量子力学的奇异性质远不止于此。在本节中，我们将深入探讨另一个令人着迷的概念——量子纠缠，以及与之相关的EPR佯谬和贝尔态的非定域性。这些概念不仅挑战了经典物理学的核心假设，还引发了关于宇宙本质的深刻哲学思考。

一、量子纠缠的起源与定义

1.2.1 量子纠缠的发现

量子纠缠的概念最早可以追溯到20世纪30年代。当时，量子力学的哥本哈根解释已经逐渐被物理学家们接受，但爱因斯坦（Albert Einstein）、波多尔斯基（Boris Podolsky）和罗森（Nathan Rosen）三位物理学家对量子力学的完备性提出了质疑。

1935年，爱因斯坦、波多尔斯基和罗森发表了一篇题为《Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?》的论文，这篇论文后来被称为EPR论文。在论文中，他们提出了一个思想实验，旨在证明量子力学是不完备的。

EPR思想实验：

假设有两个粒子A和B，它们曾经相互作用过，然后彼此分离。
根据量子力学的描述，即使粒子A和B相距遥远，它们的量子态仍然是相互关联的。
对粒子A进行测量，例如测量其位置或动量，会立即影响粒子B的状态。

爱因斯坦等人认为，这种“幽灵般的超距作用”（spooky action at a distance）与相对论中信息传递速度不能超过光速的原则相矛盾。因此，他们得出结论，量子力学是不完备的，必须存在一些隐藏的变量来解释这种关联。

1.2.2 量子纠缠的定义

量子纠缠是指两个或多个量子系统之间存在一种特殊的关联，即使它们相距遥远，其量子态仍然相互依赖。具体来说：

纠缠态： 如果两个或多个量子系统的量子态不能被表示为各个子系统量子态的直积，则称这些系统处于纠缠态。
数学表示： 假设有两个量子比特A和B，它们的纠缠态可以表示为：

其中，∣0⟩ 和 ∣1⟩ 是量子比特的基本状态。

在这个例子中，量子比特A和B的量子态是相互关联的：

如果测量A得到 ∣0⟩，那么B必定处于 ∣0⟩。
如果测量A得到 ∣1⟩，那么B必定处于 ∣1⟩。

这种关联是瞬时的，不受距离限制，即使A和B相距遥远。

二、EPR佯谬：量子力学的挑战

1.2.3 EPR佯谬的提出

EPR论文的核心是提出了一个佯谬，旨在证明量子力学是不完备的。EPR佯谬可以概括如下：

1.完备性条件：如果一个物理理论的预测是完备的，那么物理实在的每一个元素都必须在这个理论中有对应的元素。

2.物理实在的标准：如果我们能够精确地预测一个物理量的值，而不对系统进行任何干扰，那么这个物理量对应于一个物理实在的元素。

3.量子力学的预测：对于处于纠缠态的两个粒子，对一个粒子的测量可以立即影响另一个粒子的状态。

4.矛盾：根据上述条件，量子力学预测的瞬时影响意味着存在一种超距作用，这与相对论相矛盾。因此，量子力学是不完备的。

1.2.4 爱因斯坦的隐变量理论

爱因斯坦认为，量子力学的概率解释只是表面现象，背后一定存在某种更深层次的机制，即隐变量，它们决定了测量结果。

隐变量理论： 假设存在一些隐藏的变量，它们决定了量子系统的状态和测量结果。
局域性： 隐变量理论必须满足局域性条件，即信息传递速度不能超过光速。

爱因斯坦相信，引入隐变量可以解释量子纠缠现象，并恢复经典物理学的局域性和因果性。

三、贝尔不等式：量子纠缠的实验检验

1.2.5 贝尔不等式的提出

1964年，约翰·贝尔（John S. Bell）发表了一篇题为《On the Einstein Podolsky Rosen Paradox》的论文，提出了一个不等式，为检验量子纠缠提供了实验依据。

贝尔不等式：

假设存在隐变量，并且隐变量理论满足局域性条件。
贝尔推导出一个不等式，即贝尔不等式，它对某些可观测量的期望值施加了限制。

贝尔不等式的推导基于以下假设：

1.局域性：信息传递速度不能超过光速。

2.实在性：物理实在的元素是独立于观测的。

3.自由意志：实验者可以自由选择测量哪些物理量。

1.2.6 贝尔不等式的实验验证

自贝尔不等式提出以来，科学家们进行了多次实验来检验它。其中最著名的实验包括：

阿兰·阿斯派克特（Alain Aspect）实验（1981-1982）： 首次严格地验证了贝尔不等式，结果表明量子力学的预测是正确的，贝尔不等式被违反。
安东·蔡林格（Anton Zeilinger）实验（1998）： 进一步验证了量子纠缠的非局域性，并排除了实验漏洞。

这些实验结果一致表明：

量子纠缠现象是真实的。
贝尔不等式被违反。
隐变量理论如果满足局域性条件，则无法解释量子纠缠。

1.2.7 量子纠缠的非局域性

贝尔不等式的违反意味着：

量子力学违反了局域性原则。
量子纠缠是一种非局域的关联。
量子系统之间的关联是瞬时的，不受距离限制。

这种非局域性并不意味着信息可以超光速传递，因为量子纠缠本身并不能传递信息。但是，它确实挑战了我们对空间和时间的传统理解。

四、量子纠缠的应用

1.2.8 量子通信

量子纠缠是量子通信的基础：

量子密钥分发（QKD）： 利用量子纠缠可以安全地分发密钥，因为任何窃听行为都会破坏量子态，从而被检测到。
量子隐形传态： 量子纠缠可以用于实现量子隐形传态，即在量子态不传输的情况下，将量子态从一个位置传递到另一个位置。

1.2.9 量子计算

量子纠缠是量子计算的核心资源：

量子纠缠态： 量子计算机可以利用纠缠态来实现并行计算。
量子门操作： 量子纠缠可以用于实现量子门操作，从而实现量子计算。

1.2.10 量子传感

量子纠缠可以用于制造高精度的量子传感器：

量子纠缠增强的测量： 利用量子纠缠可以提高测量的精度，例如原子钟、量子磁力计等。

五、哲学思考：量子纠缠的启示

量子纠缠现象对经典世界观提出了严峻挑战，引发了深刻的哲学思考。

1.2.11 实在性问题

量子纠缠表明，物理实在的元素之间存在一种非局域的关联。
这种关联是瞬时的，不受距离限制，挑战了经典物理学中关于空间和时间的概念。

1.2.12 因果性问题

量子纠缠似乎暗示着一种超距作用，但这种作用并不能传递信息。
这意味着因果关系在量子力学中具有不同的含义。

1.2.13 局域性原则的挑战

贝尔不等式的违反表明，量子力学违反了局域性原则。
这对爱因斯坦的相对论和经典物理学的基础提出了挑战。

1.2.14 量子力学的解释问题

量子纠缠现象进一步凸显了量子力学的解释问题。
现有的解释，例如哥本哈根解释、多世界解释等，都无法完全解释量子纠缠的非局域性。

六、结语

量子纠缠是量子力学中最神秘、最令人着迷的现象之一。它揭示了量子系统之间存在一种非局域的关联，挑战了经典物理学的核心假设，并引发了关于宇宙本质的深刻哲学思考。

EPR佯谬和贝尔不等式为检验量子纠缠提供了理论框架和实验依据，而实验结果则表明，量子纠缠现象是真实的，量子力学是非局域的。

量子纠缠不仅具有重要的理论意义，还在量子通信、量子计算、量子传感等领域具有广阔的应用前景。随着量子技术的发展，量子纠缠的研究将继续推动科学技术的进步，并加深我们对量子力学的理解。

总而言之，量子纠缠现象为我们打开了一扇通往未知世界的大门，而探索这片神秘领域的过程，将继续激励着无数科学家和哲学家不断前行。

1.3 不可克隆定理：量子信息学的保护神

亲爱的读者，欢迎继续我们的量子力学与量子信息学之旅。在前两节中，我们探讨了叠加态与坍缩以及量子纠缠，这些概念揭示了量子世界的奇异本质，并挑战了我们对现实的理解。在本节中，我们将深入探讨另一个至关重要的概念——不可克隆定理（No-Cloning Theorem）。这个定理不仅是量子力学的基本原理之一，更是量子信息学的基石，为量子通信和量子计算提供了重要的安全保障。

一、不可克隆定理的起源与定义

1.3.1 不可克隆定理的提出

不可克隆定理最早由威廉·伍特斯（W. K. Wootters）和沃伊切赫·祖莱克（Wojciech H. Zurek）在1982年的一篇论文中提出。该定理指出，在量子力学中，不存在一个物理过程可以完美地复制一个未知的量子态。

1.3.2 定理的数学表述

为了更好地理解不可克隆定理，我们需要从数学角度进行阐述。

假设我们有一个未知的量子态 ∣ψ⟩，我们希望将其复制到另一个量子系统上，即：

其中，∣A⟩ 是初始的辅助态。

不可克隆定理表明，不存在一个幺正算符 U 可以实现上述变换，除非 ∣ψ⟩ 是已知的，或者属于一组特定的量子态。

二、不可克隆定理的物理意义

1.3.3 量子态的独特性

不可克隆定理揭示了量子态的独特性：

不可复制性： 量子态不能被完美复制。
不可区分性： 量子态的测量结果具有概率性，无法通过测量完全确定量子态。

这种独特性是量子力学与经典物理学的一个重要区别。在经典物理学中，物体的状态可以被精确测量和复制，例如，我们可以复制一本书或一张光盘的内容。

1.3.4 量子态的脆弱性

量子态的不可克隆性也意味着量子态是脆弱的：

测量干扰： 对量子态的测量会不可避免地改变其状态。
退相干： 量子系统与环境相互作用会导致量子相干性的丧失。

这种脆弱性使得量子态难以保持和操控，但也为量子信息的安全提供了保障。

1.3.5 量子信息学的基石

不可克隆定理是量子信息学的基石，它为量子通信和量子计算提供了重要的安全保障：

量子密钥分发： 不可克隆定理保证了量子密钥分发的安全性，因为任何窃听行为都会不可避免地改变量子态，从而被检测到。
量子计算： 不可克隆定理意味着量子信息不能被简单地复制，这为量子计算中的错误校正带来了挑战，但也为量子计算的安全性提供了保障。

三、不可克隆定理的应用

1.3.6 量子密钥分发（QKD）

量子密钥分发是量子信息学最重要的应用之一，其安全性基于不可克隆定理。

BB84协议：

1984年，查尔斯·贝内特（Charles H. Bennett）和吉勒斯·布拉萨德（Gilles Brassard）提出了BB84协议，这是第一个量子密钥分发协议。
该协议利用量子态的不可克隆性和测量干扰来实现安全的密钥分发。

协议流程：

1.量子态传输：爱丽丝（发送者）随机选择一组量子态（例如，单个光子）并将其发送给鲍勃（接收者）。这些量子态可以是水平的、垂直的、45度或135度偏振态。

2.测量：鲍勃随机选择测量基（例如，水平和垂直或45度和135度）来测量接收到的量子态。

3.通信：爱丽丝和鲍勃通过经典信道公开交流他们使用的测量基，但不会透露测量结果。

4.密钥生成：对于那些鲍勃使用与爱丽丝相同的测量基的情况，测量结果可以作为密钥的一部分。

5.安全性：由于任何窃听行为都会改变量子态，爱丽丝和鲍勃可以通过比较部分密钥来检测是否存在窃听。

1.3.7 量子秘密共享

量子秘密共享是利用量子纠缠实现的一种安全的信息共享方案。

协议流程：

1.纠缠态制备：爱丽丝制备一组纠缠态（例如，贝尔态）并将它们分发给鲍勃和查理。

2.信息编码：爱丽丝对其中一部分纠缠态进行操作，将她想要共享的信息编码到量子态中。

3.测量：鲍勃和查理对接收到的量子态进行测量。

4.信息恢复：通过经典通信，爱丽丝、鲍勃和查理可以合作恢复出共享的信息。

由于不可克隆定理，任何窃听者都无法复制纠缠态，因此量子秘密共享具有很高的安全性。

1.3.8 量子计算中的量子态复制

虽然不可克隆定理表明量子态不能被完美复制，但在量子计算中，我们仍然需要复制量子态来进行量子纠错。

量子复制机：

量子复制机是一种可以近似复制量子态的装置。
它可以复制一组已知的量子态，但不能复制任意未知的量子态。

量子纠错：

量子纠错利用量子复制机来复制量子信息，并通过冗余编码来纠正错误。
由于不可克隆定理，量子纠错面临着独特的挑战，但也在不断发展。

四、不可克隆定理的哲学思考

1.3.9 量子态的独特性与经典物理学的区别

不可克隆定理强调了量子态的独特性，这与经典物理学中的可复制性形成鲜明对比。

经典物理学： 物体的状态可以被精确测量和复制。
量子力学： 量子态的测量具有概率性，且不能被完美复制。

这种区别反映了量子力学与经典物理学在本质上的不同，也引发了关于量子力学解释的哲学思考。

1.3.10 量子信息与经典信息的区别

不可克隆定理也揭示了量子信息与经典信息的区别：

经典信息： 可以被复制和克隆。
量子信息： 不能被完美复制。

这种区别对信息论和计算理论产生了深远的影响。

1.3.11 量子力学的解释问题

不可克隆定理对量子力学的解释问题提出了新的挑战：

哥本哈根解释： 强调测量过程的重要性，但无法解释不可克隆性。
多世界解释： 认为所有可能的量子态都存在于不同的平行宇宙中，但无法解释量子信息的独特性。
量子信息解释： 将量子态看作是一种信息载体，强调量子信息与经典信息的区别。

五、结语

不可克隆定理是量子信息学的基石，它揭示了量子态的独特性和脆弱性，为量子通信和量子计算提供了重要的安全保障。

通过深入理解不可克隆定理，我们不仅可以更好地理解量子力学的原理，还能更深刻地思考量子信息与经典信息的区别，以及量子力学的解释问题。

量子信息学是一个充满活力和挑战的领域，而不可克隆定理作为其核心原理之一，将继续推动着量子技术的发展，并加深我们对量子世界的理解。

总而言之，不可克隆定理为我们理解量子信息学提供了一个重要的视角，它提醒我们，量子世界是一个充满奇异性和复杂性的领域，而探索这片神秘领域的过程，将继续激励着无数科学家和哲学家不断前行。

第2章量子计算数学基石

希尔伯特空间漫步：狄拉克符号的几何化理解
张量积的魔法：多量子比特系统的维度爆炸
酉变换之道：量子门操作的保范性原理

2.1 希尔伯特空间漫步：狄拉克符号的几何化理解

欢迎来到量子计算数学基石的旅程。在这一章中，我们将深入探讨量子力学和量子计算背后的数学结构，这些数学工具不仅为描述量子系统提供了精确的语言，还为理解和设计量子算法奠定了基础。在本节中，我们将聚焦于希尔伯特空间和狄拉克符号，并尝试以一种几何化的视角来理解它们。

一、希尔伯特空间：量子力学的数学舞台

2.1.1 什么是希尔伯特空间？

希尔伯特空间（Hilbert space）是以德国数学家大卫·希尔伯特（David Hilbert）的名字命名的，它是量子力学的数学基础之一。

定义：

希尔伯特空间是一个完备的内积空间，具有以下性质：

1.线性：希尔伯特空间是一个向量空间，任意两个向量可以相加，数乘运算也满足线性性质。

2.内积：希尔伯特空间具有内积运算，它为向量之间的角度和长度提供了度量。

3.完备性：希尔伯特空间是完备的，即任何柯西序列在该空间中都收敛于一个极限。

2.1.2 量子力学中的希尔伯特空间

在量子力学中，希尔伯特空间被用来描述量子系统的状态空间：

态矢量： 量子系统的状态由希尔伯特空间中的向量（态矢量）描述。
波函数： 态矢量通常用波函数表示，例如，表示粒子ψ在位置 x 处的概率幅。
概率解释： 态矢量的内积提供了量子态的概率解释。例如，表示总概率为1。

2.1.3 狄拉克符号：量子力学的语言

为了更方便地处理量子态，物理学家保罗·狄拉克（Paul Dirac）引入了一种简洁的符号体系，称为狄拉克符号。

2.1.3.1 狄拉克符号的基本元素

右矢（ket）： 表示量子态的向量，记作。
左矢（bra）： 表示量子态的对偶向量，记作。
内积： 两个量子态的内积记作，它是一个复数。

2.1.3.2 狄拉克符号的优势

简洁性： 狄拉克符号提供了一种简洁的方式来表示量子态和操作。
几何直观： 狄拉克符号可以与几何直观联系起来，例如，可以看作是一个向量，可以看作是一个线性泛函。
运算规则： 狄拉克符号具有明确的运算规则，例如：

二、几何化理解：希尔伯特空间中的几何图像

2.1.4 态矢量的几何解释

在希尔伯特空间中，量子态可以看作是高维空间中的向量：

向量长度： 态矢量的长度由内积给出，即。由于量子态是归一化的，其长度为1。
向量方向： 态矢量的方向表示量子态的相位信息。

2.1.4.1 量子态的叠加

量子态的叠加可以看作是两个或多个向量的线性组合：

其中，c1 和 c2 是复数，满足。

几何上，这意味着位于由和张成的平面上。

2.1.4.2 量子态的测量

量子态的测量可以看作是将态矢量投影到一个特定的方向上：

投影算符： 测量一个物理量对应的算符可以看作是一个投影算符。
测量结果： 测量结果对应于投影后态矢量的长度平方，即概率。

例如，测量一个量子比特的状态，可以看作是将态矢量投影到 ∣0⟩∣0⟩ 或 ∣1⟩∣1⟩ 方向上。

2.1.4.3 量子纠缠的几何解释

量子纠缠态的几何解释更加复杂：

纠缠态： 纠缠态不能被分解为两个子系统的直积。例如，贝尔态：

不能被表示为。
几何意义： 纠缠态对应于希尔伯特空间中的高维结构，不能被简单地分解为低维子空间。

2.1.5 狄拉克符号的几何化理解

狄拉克符号可以与几何图像联系起来：

右矢（ket）： 可以看作是高维空间中的向量。
左矢（bra）： 可以看作是对偶空间中的线性泛函。
内积：可以看作是将 ∣ψ⟩ 投影到 ∣ϕ⟩ 方向上的分量。

2.1.5.1 算符的几何解释

量子力学中的算符可以看作是对向量进行线性变换：

幺正算符： 幺正算符保持向量的内积不变，对应于旋转或反射操作。
厄米算符： 厄米算符对应于可观测量的算符，其特征值是实数。

例如，泡利矩阵是厄米算符，它们对应于量子比特的不同可观测量。

2.1.5.2 量子门操作的几何解释

量子门操作可以看作是对量子态进行幺正变换：

单量子比特门： 例如，泡利矩阵、哈达玛门（Hadamard gate）等，可以看作是对量子态进行旋转或反射。
多量子比特门： 例如，CNOT门，可以看作是对量子态进行纠缠操作。

几何上，量子门操作对应于希尔伯特空间中的旋转或反射操作。

三、量子计算中的希尔伯特空间和狄拉克符号

2.1.6 量子比特的状态空间

一个量子比特的状态空间是一个二维希尔伯特空间：

基态： 通常选择 ∣0⟩ 和 ∣1⟩ 作为基态。
任意态： 任意量子比特态可以表示为：

其中，α 和 β 是复数，满足。

2.1.7 多量子比特系统

多量子比特系统的状态空间是张量积希尔伯特空间：

张量积： 两个量子比特的状态空间是，其维数为 2×2=4。
基态： 例如，两个量子比特的基态为 ∣00⟩, ∣01⟩, ∣10⟩, ∣11⟩。
任意态： 任意两个量子比特态可以表示为：

其中，α, β, γ, δ 是复数，满足。

2.1.8 量子算法中的几何图像

许多量子算法都可以用希尔伯特空间中的几何图像来解释：

量子傅里叶变换： 可以看作是对量子态进行旋转操作。
量子相位估计算法： 可以看作是对量子态进行相位旋转。
量子搜索算法： 可以看作是在希尔伯特空间中寻找特定状态的过程。

四、总结

在本节中，我们对希尔伯特空间和狄拉克符号进行了深入探讨，并尝试从几何化的角度来理解它们：

希尔伯特空间： 为量子力学提供了数学框架，描述了量子系统的状态空间。
狄拉克符号： 提供了一种简洁而强大的符号体系，使得量子态和操作更容易处理。
几何化理解： 通过将量子态看作是高维空间中的向量，我们可以更直观地理解量子力学的概念和操作。

这种几何化的视角不仅有助于我们更好地理解量子力学的原理，还为我们设计和分析量子算法提供了新的思路。总而言之，希尔伯特空间和狄拉克符号是量子力学的核心工具，它们为我们探索量子世界的奥秘提供了强大的数学武器。希望本小节的内容能够激发您对量子力学的兴趣，并为您的量子计算学习之旅提供帮助。加油，让我们在后续的小节继续深入学习！

2.2 张量积的魔法：多量子比特系统的维度爆炸

欢迎继续深入量子计算的奇妙世界。在上一节中，我们探讨了希尔伯特空间和狄拉克符号，它们为描述量子态提供了强大的数学工具。在本节中，我们将聚焦于张量积，一个在量子计算中无处不在的重要概念。张量积不仅是描述多量子比特系统的关键，还揭示了量子计算复杂性的根源，即所谓的“维度爆炸”。让我们一起踏上这段探索之旅。

一、张量积的基本概念

2.2.1 什么是张量积？

张量积（tensor product）是线性代数中的一个重要运算，用于构造更高维度的向量空间。在量子力学和量子计算中，张量积被用来描述复合量子系统的状态空间。

定义：

假设 V 和 W 是两个向量空间，其维数分别为 m 和 n。那么，它们的张量积 V⊗W 是一个新的向量空间，其维数为 m×n。

2.2.2 张量积的性质

双线性： 张量积对每个分量都是线性的，即：
分配律： 张量积对加法满足分配律。
结合律： 张量积是结合的，即 (U⊗V)⊗W=U⊗(V⊗W)。

2.2.3 张量积的表示

在量子力学中，张量积通常用符号 ⊗ 表示。例如：

如果 ∣ψ⟩ 和 ∣ϕ⟩ 是两个量子态，那么它们的张量积表示为：

∣ψ⟩⊗∣ϕ⟩
为了简化表示，通常省略 ⊗ 符号，直接写作：

∣ψ⟩∣ϕ⟩或∣ψϕ⟩

二、多量子比特系统的状态空间

2.2.4 单量子比特状态空间

一个量子比特的状态空间是一个二维希尔伯特空间，其基态通常表示为：

任意单量子比特态可以表示为：

其中，α 和 β 是复数，满足。

2.2.5 双量子比特状态空间

两个量子比特的状态空间是单量子比特状态空间的张量积：

其维数为 2×2=4。基态为：

任意双量子比特态可以表示为：

其中，α, β, γ, δ 是复数，满足。

2.2.6 多量子比特状态空间

类似地，n 个量子比特的状态空间是 n 个单量子比特状态空间的张量积：

其维数为。基态为：

例如，三个量子比特的状态空间维数为，其基态为：

三、维度爆炸：量子计算复杂性的根源

2.2.7 维度爆炸的含义

维度爆炸（dimensionality explosion）指的是，随着量子比特数的增加，量子系统的状态空间维度呈指数级增长。

单量子比特： 2维
双量子比特： 4维
三量子比特： 8维
n个量子比特： 维

2.2.8 维度爆炸的影响

计算能力： 维度爆炸赋予了量子计算机强大的并行计算能力。一个量子比特可以同时表示0和1，两个量子比特可以同时表示00, 01, 10, 11四种状态，依此类推。
存储需求： 维度爆炸也意味着量子计算机需要存储和处理的信息量呈指数级增长。例如，一个包含1000个量子比特的量子计算机，其状态空间维度为 2^1000，远远超过了经典计算机的处理能力。
复杂性： 维度爆炸使得量子系统的行为变得极其复杂，难以用经典计算机进行模拟。

2.2.9 量子计算的优势

维度爆炸是量子计算相对于经典计算的主要优势之一：

并行性： 量子计算机可以利用量子叠加态同时处理大量信息。
指数加速： 对于某些特定问题，量子计算机可以实现指数级的加速，例如，Shor算法可以在多项式时间内分解大整数，而经典算法则需要指数时间。

2.2.10 量子计算的挑战

然而，维度爆炸也带来了巨大的挑战：

量子纠错： 维度爆炸使得量子系统更容易受到噪声和退相干的影响，需要更强大的量子纠错技术。
量子算法设计： 寻找可以利用维度爆炸优势的量子算法是一个巨大的挑战。
量子硬件实现： 构建能够控制和处理大量量子比特的量子硬件是一个巨大的工程挑战。

四、张量积在量子计算中的应用

2.2.11 量子纠缠

张量积是描述量子纠缠的基础：

纠缠态： 纠缠态是张量积空间中的特殊状态，不能被分解为各个子系统状态的直积。
贝尔态： 例如，贝尔态：

是双量子比特张量积空间中的一个纠缠态。

2.2.12 量子门操作

量子门操作可以看作是对量子态进行张量积和线性变换：

单量子比特门： 例如，泡利矩阵、哈达玛门等，可以看作是对单个量子比特进行张量积和线性变换。
多量子比特门： 例如，CNOT门，可以看作是对两个量子比特进行张量积和受控操作。

2.2.13 量子算法

许多量子算法都利用了张量积和维度爆炸的优势：

量子傅里叶变换： 可以看作是对量子态进行张量积和傅里叶变换。
量子相位估计算法： 可以看作是对量子态进行张量积和相位估计。
量子搜索算法： 可以看作是在张量积空间中搜索特定状态。

五、总结

在本节中，我们深入探讨了张量积的概念及其在量子计算中的应用：

张量积： 提供了构造高维向量空间的方法，是描述多量子比特系统的基础。
维度爆炸： 揭示了量子计算复杂性的根源，赋予了量子计算机强大的计算能力。
量子纠缠： 张量积是描述量子纠缠的关键工具。
量子门操作： 张量积和线性变换是实现量子门操作的基础。

维度爆炸既是量子计算的优势，也是其挑战所在。它为量子计算提供了指数级的加速潜力，但也带来了巨大的技术挑战。

总而言之，张量积是量子计算的核心概念，它为我们理解量子计算的本质和潜力提供了重要的视角。希望这段旅程能够加深您对量子计算的理解，并为您的量子计算学习之旅提供一些启示。

2.3 酉变换之道：量子门操作的保范性原理

欢迎继续深入量子计算的数学世界。在前两节中，我们探讨了希尔伯特空间和张量积，这些概念为我们理解量子态和量子系统的结构提供了基础。在本节中，我们将聚焦于酉变换（Unitary Transformation）和量子门操作，并深入理解它们背后的保范性原理（Preservation of Norm）。这些概念不仅是量子计算的理论基石，也是实现量子计算的实际工具。让我们一起踏上这段探索之旅。

一、酉变换的基本概念

2.3.1 什么是酉变换？

在数学中，酉变换是一种保持内积不变的线性变换。在量子力学和量子计算中，酉变换被用来描述量子态的演化。

定义：

一个线性变换 U 被称为酉变换，如果它满足以下条件：

1. 幺正性（Unitarity）： U 的共轭转置是其逆，即：

其中，�I 是单位矩阵。

2. 保内积性： 酉变换保持向量的内积不变，即对于任意两个向量 ∣ψ⟩ 和 ∣ϕ⟩，有：

2.3.2 酉变换的性质

保范性： 酉变换保持向量的范数不变，即：

其中，表示向量的欧几里得范数。
可逆性： 酉变换是可逆的，其逆变换也是酉变换。
保概率性： 酉变换保持量子态的概率分布不变，即：

二、量子门操作：酉变换在量子计算中的应用

2.3.3 量子门的基本概念

在量子计算中，量子门（Quantum Gate）是实现量子计算的基本操作单元。量子门可以看作是对量子态进行酉变换的装置。

定义：

一个量子门是一个幺正矩阵 U，它对量子态进行如下变换：

2.3.4 常见的量子门

单量子比特门：
- 泡利矩阵：
  
  泡利矩阵是厄米矩阵，也是酉矩阵，它们对应于量子比特的不同可观测量。
- 哈达玛门（Hadamard Gate）：
  
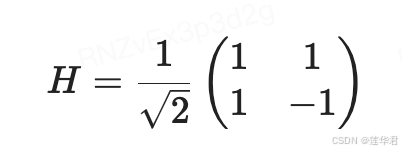
  哈达玛门将 ∣0⟩ 转换为，将 ∣1⟩ 转换为。
- 相位门（Phase Gate）：
  
  相位门将 ∣1⟩∣1⟩ 的相位旋转 90∘90∘。
- 8π/8 门（T Gate）：

8π/8 门将 ∣1⟩ 的相位旋转 45°。

双量子比特门：
- CNOT门（Controlled-NOT Gate）：
  
  CNOT门以第一个量子比特为控制比特，第二个量子比特为目标比特。当控制比特为 ∣1⟩ 时，交换目标比特的 ∣0⟩ 和 ∣1⟩。
- SWAP门：
  
  SWAP门将两个量子比特的状态交换。

2.3.5 量子门操作的保范性

量子门操作是酉变换，因此具有保范性：

保概率： 量子门操作不会改变量子态的概率分布。
保内积： 量子门操作不会改变量子态之间的内积。

这意味着，量子门操作是量子态演化的可逆过程，不会导致信息的丢失或增加。

2.3.6 量子门操作的组合

量子门操作可以组合起来，形成更复杂的量子电路：

序列组合： 多个量子门依次作用，相当于将它们的酉矩阵相乘。
并行组合： 多个量子门同时作用，相当于对量子态进行张量积和酉变换。

例如，一个简单的量子电路可以表示为：

其中，是量子门。

三、保范性原理：量子计算的基石

2.3.7 保范性的重要性

保范性是量子计算的一个关键特性：

信息保护： 保范性确保了量子信息在量子门操作过程中不会丢失或改变。
可逆性： 保范性意味着量子门操作是可逆的，这使得量子计算具有可逆计算的特性。
幺正演化： 保范性是量子力学中幺正演化的体现，即量子系统的演化由幺正算符描述。

2.3.8 保范性与量子纠错

保范性对于量子纠错至关重要：

量子纠错码： 量子纠错码利用保范性来检测和纠正量子错误。
错误检测： 通过测量量子态的保范性，可以检测出量子错误。
错误纠正： 利用保范性，可以设计出纠正量子错误的操作。

2.3.9 保范性与量子算法的实现

保范性是实现量子算法的基础：

量子算法设计： 量子算法必须满足保范性，以确保计算结果的正确性。
量子电路实现： 量子电路中的所有量子门操作都必须满足保范性。

四、量子计算中的酉变换

2.3.10 量子态的演化

在量子计算中，量子态的演化由酉变换描述：

时间演化： 量子态的时间演化由哈密顿算符 H 描述，即：

其中，是一个酉算符。
量子门操作： 量子门操作可以看作是对量子态进行离散的时间演化。

2.3.11 量子算法的实现

许多量子算法都依赖于酉变换来实现：

量子傅里叶变换： 可以看作是对量子态进行酉变换。
量子相位估计算法： 可以看作是对量子态进行相位旋转的酉变换。
量子搜索算法： 可以看作是对量子态进行特定酉变换的过程。

2.3.12 量子计算的局限性

保范性也带来了量子计算的局限性：

不可克隆定理： 由于保范性，量子态不能被完美克隆。
不可删除定理： 同样由于保范性，量子态不能被完美删除。

五、总结

在本节中，我们深入探讨了酉变换和量子门操作的保范性原理：

酉变换： 保持内积和范数不变的线性变换，是量子态演化的数学描述。
量子门操作： 量子计算的基本操作单元，是实现量子算法的工具。
保范性原理： 保证了量子信息在量子计算过程中的完整性和可逆性，是量子计算的理论基石。

保范性原理不仅是量子力学的基本原理，也是量子计算的核心特性。它确保了量子信息的安全性和可逆性，但也带来了量子计算的独特挑战。

总而言之，酉变换和保范性原理是量子计算的灵魂，它们为我们理解量子计算的本质和潜力提供了重要的视角。希望这段旅程能够加深您对量子计算的理解，并为您的量子计算学习之旅提供一些启示。

第3章量子比特实现之路

物理载体巡礼：超导电路、离子阱与拓扑量子比特
量子态制备术：激光冷却与微波脉冲的操控艺术
退相干对抗战：T1/T2时间的生死时速

3.1 物理载体巡礼：超导电路、离子阱与拓扑量子比特

欢迎来到量子计算实现之路的第三章。在前两章中，我们深入探讨了量子力学的数学基础和量子计算的基本原理。然而，要将量子计算的强大潜力转化为现实，我们需要找到合适的物理载体来实现量子比特（qubit）。在本节中，我们将巡礼三种主要的量子比特实现方案：超导电路、离子阱和拓扑量子比特。这些方案各具特色，代表了当前量子计算硬件发展的前沿方向。让我们一同踏上这段探索之旅。

一、超导电路：量子计算的前沿阵地

3.1.1 超导量子比特的原理

超导量子比特是利用超导电路中的约瑟夫森结（Josephson junction）来实现量子态的量子比特。约瑟夫森结是由两个超导体之间夹着一层薄薄的绝缘体构成的器件。

主要特点：

宏观量子态： 超导量子比特利用宏观尺度的电路来实现量子态，这使得它们相对容易控制和测量。
可扩展性： 超导电路可以利用现有的半导体制造技术进行大规模集成。
快速操作速度： 超导量子比特的操作速度通常在纳秒量级。

3.1.2 超导量子比特的类型

电荷量子比特（Charge Qubit）： 基于单个库珀对（Cooper pair）在两个超导岛之间的隧穿效应。电荷量子比特对电荷噪声敏感，但操作速度快。
磁通量子比特（Flux Qubit）： 基于超导环中磁通量的量子化状态。磁通量子比特对磁通噪声敏感，但相干时间较长。
相位量子比特（Phase Qubit）： 基于约瑟夫森结中相位差的量子化状态。相位量子比特对相位噪声敏感，但相干时间较长。

3.1.3 超导量子比特的优缺点

优点：

可扩展性强： 可以利用现有的半导体制造技术进行大规模集成。
操作速度快： 量子门操作速度通常在纳秒量级。
与经典电子器件兼容： 可以利用现有的电子技术进行控制和测量。

缺点：

相干时间有限： 超导量子比特的相干时间通常在微秒量级，需要强大的量子纠错技术。
对环境敏感： 需要极低温环境（通常在 10-20 mK）来抑制热噪声。
制造工艺复杂： 需要精确的制造工艺来控制约瑟夫森结的特性。

3.1.4 超导量子计算的代表

谷歌（Google）： 谷歌的量子计算团队开发了名为“悬铃木”（Sycamore）的超导量子处理器，并在2019年宣布实现了“量子优越性”，即量子计算机在特定任务上超越了经典超级计算机。
IBM： IBM 拥有强大的超导量子计算平台，提供了基于云的量子计算服务，并不断推动超导量子比特技术的发展。
Rigetti Computing： 这是一家专注于超导量子计算的初创公司，致力于构建商业化的量子计算机。

二、离子阱：精确操控的典范

3.1.5 离子阱量子比特的原理

离子阱量子比特是利用电磁场囚禁的单个离子来实现量子态的量子比特。常见的离子阱类型包括保罗阱（Paul trap）和彭宁阱（Penning trap）。

主要特点：

单离子操控： 可以精确操控单个离子的量子态，实现高保真度的量子门操作。
长相干时间： 离子阱量子比特的相干时间通常在秒到分钟量级。
高保真度： 量子门操作的保真度通常在 99.9% 以上。

3.1.6 离子阱量子比特的类型

钙离子（Ca+）： 钙离子具有简单的能级结构和良好的相干性，是离子阱量子计算中常用的离子。
铍离子（Be+）： 铍离子对磁场噪声不敏感，是另一种常用的离子。
镱离子（Yb+）： 镱离子具有较长的相干时间和良好的光学特性。

3.1.7 离子阱量子比特的优缺点

优点：

相干时间长： 离子阱量子比特的相干时间远长于超导量子比特。
高保真度： 量子门操作的保真度高。
可扩展性： 理论上可以通过离子链或离子阱阵列实现大规模集成。

缺点：

操作速度慢： 量子门操作速度通常在微秒到毫秒量级。
对激光控制要求高： 需要精确的激光控制系统来实现量子态的操控。
可扩展性挑战： 虽然理论上可行，但实现大规模离子阱量子计算机仍然面临技术挑战。

3.1.8 离子阱量子计算的代表

霍尼韦尔（Honeywell）： 霍尼韦尔在离子阱量子计算领域处于领先地位，推出了多款商业化的离子阱量子计算机。
IonQ： 这是一家专注于离子阱量子计算的初创公司，声称其量子计算机具有最高的量子体积。
奥地利的因斯布鲁克大学（University of Innsbruck）： 该大学的量子物理学家团队在离子阱量子计算领域做出了许多开创性的工作。

三、拓扑量子比特：稳健的未来之星

3.1.9 拓扑量子比特的原理

拓扑量子比特是基于拓扑量子态的量子比特，其量子信息存储在拓扑不变量中，具有很强的抗干扰能力。

主要特点：

拓扑保护： 拓扑量子比特的量子信息对局部扰动不敏感，具有很强的抗噪声能力。
低错误率： 理论上，拓扑量子比特的错误率可以降低到非常低的水平。
长相干时间： 拓扑量子比特的相干时间可以很长。

3.1.10 拓扑量子比特的类型

马约拉纳零模（Majorana Zero Mode）： 基于马约拉纳费米子的拓扑量子态。马约拉纳零模是实现拓扑量子计算的一种候选方案。
非阿贝尔任意子（Non-Abelian Anyon）： 基于非阿贝尔任意子的拓扑量子态，例如，斐波那契任意子（Fibonacci Anyon）。

3.1.11 拓扑量子比特的优缺点

优点：

强大的抗干扰能力： 拓扑保护使得拓扑量子比特对环境噪声具有很强的免疫力。
低错误率： 拓扑量子比特具有很低的错误率，适合实现容错量子计算。
长相干时间： 拓扑量子比特的相干时间可以很长。

缺点：

实现难度大： 拓扑量子比特的实现需要克服许多技术挑战，例如，制造稳定的拓扑量子态。
可扩展性挑战： 拓扑量子比特的可扩展性仍然是一个未解决的问题。
缺乏实验验证： 目前，拓扑量子计算仍然处于实验验证阶段，距离实用化还有很长的路要走。

3.1.12 拓扑量子计算的代表

微软（Microsoft）： 微软在拓扑量子计算领域投入了大量资源，目标是实现基于马约拉纳零模的拓扑量子计算机。
谷歌（Google）： 谷歌也在探索拓扑量子计算的潜力，并研究非阿贝尔任意子。
学术界： 许多大学和研究机构都在积极研究拓扑量子计算，例如，荷兰代尔夫特理工大学（Delft University of Technology）和美国加州大学圣巴巴拉分校（University of California, Santa Barbara）。

四、总结

在本节中，我们巡礼了三种主要的量子比特实现方案：

超导电路： 利用超导电路中的约瑟夫森结实现量子态，具有可扩展性强、操作速度快的优点，但相干时间有限。
离子阱： 利用电磁场囚禁的单个离子实现量子态，具有长相干时间和高保真度的优点，但操作速度慢。
拓扑量子比特： 基于拓扑量子态的量子比特，具有强大的抗干扰能力和低错误率的优点，但实现难度大。

每种方案都有其独特的优势和挑战，目前还没有一种方案能够完全满足量子计算的所有要求。未来，量子比特实现方案的多样化发展将为量子计算的实现提供更多的可能性。

总而言之，量子比特的实现是量子计算发展的关键一步，而探索不同的物理载体和实现方案，将继续推动着量子计算技术的不断进步。希望这段旅程能够加深您对量子比特实现方案的理解，并为您的量子计算学习之旅提供一些启示。

3.2 量子态制备术：激光冷却与微波脉冲的操控艺术

欢迎继续深入量子比特实现之路的探索。在上一节中，我们探讨了实现量子比特的几种主要物理载体，包括超导电路、离子阱和拓扑量子比特。然而，无论选择哪种物理载体，量子态的制备都是构建量子计算机的关键步骤之一。在本节中，我们将深入探讨两种关键的量子态制备技术：激光冷却和微波脉冲操控。这些技术不仅展示了人类对微观世界的精确操控能力，也为实现高保真度的量子计算奠定了基础。

一、激光冷却：驯服原子的艺术

3.2.1 激光冷却的原理

激光冷却（Laser Cooling）是一种利用激光来降低原子或离子动能的技术，其核心思想是利用光子的动量传递来减速运动中的原子。

主要原理：

多普勒效应： 当原子运动时，它吸收和发射的光子频率会因多普勒效应而发生偏移。
光子反冲： 当原子吸收光子时，它会获得一个与光子运动方向相反的动量。
自发辐射： 原子在吸收光子后，会自发辐射光子，并获得一个随机的动量变化。

3.2.2 多普勒冷却

多普勒冷却是最常见的激光冷却技术：

激光配置： 将一束激光调谐到略低于原子共振频率的频率。
冷却机制： 当原子向激光源运动时，由于多普勒效应，它会看到更高的激光频率，更容易吸收光子，并获得一个与运动方向相反的动量。
净效应： 原子在吸收和自发辐射光子的过程中，平均而言会损失动能，从而被冷却。

3.2.3 塞曼冷却和西西弗斯冷却

为了克服多普勒冷却的局限性，科学家们开发了更先进的激光冷却技术：

塞曼冷却（Zeeman Cooling）： 利用磁场来调节原子能级，从而实现更有效的冷却。
西西弗斯冷却（Sisyphus Cooling）： 通过周期性改变激光场的极化，使原子在吸收和自发辐射过程中不断“攀登”能量坡，最终达到更低的温度。

3.2.4 激光冷却的应用

离子阱量子计算： 激光冷却是制备和操控离子阱中离子的关键技术。通过激光冷却，可以将离子冷却到接近绝对零度，从而抑制热噪声，提高量子态的相干性。
原子钟： 激光冷却用于制备超冷原子，从而提高原子钟的精度。
玻色-爱因斯坦凝聚（BEC）： 激光冷却是实现玻色-爱因斯坦凝聚的关键技术。

3.2.5 激光冷却的优势与挑战

优势：

精确控制： 可以实现对原子运动的精确控制。
高效冷却： 可以将原子冷却到极低的温度（微开尔文量级）。
广泛应用： 在量子计算、精密测量等领域具有广泛应用。

挑战：

复杂性： 激光冷却系统复杂，需要精确的激光和磁场控制。
局限性： 对于某些类型的量子比特（例如，超导量子比特），激光冷却不适用。

二、微波脉冲操控：驾驭量子态的魔法

3.2.6 微波脉冲操控的原理

微波脉冲操控（Microwave Pulse Control）是一种利用微波脉冲来操控量子态的技术。在量子计算中，微波脉冲被用来实现量子门操作。

主要原理：

共振激发： 当微波脉冲的频率与量子系统的能级差共振时，会引起量子态之间的跃迁。
拉比振荡（Rabi Oscillation）： 在共振条件下，量子态会在两个能级之间来回振荡，振荡的频率和幅度由微波脉冲的强度和持续时间决定。
π脉冲和π/2脉冲： 特定强度的微波脉冲可以实现对量子态的完全翻转（π脉冲）或将其置于叠加态（π/2脉冲）。

3.2.7 量子门操作的实现

微波脉冲操控是实现量子门操作的重要手段：

单量子比特门： 例如，哈达玛门（Hadamard Gate）和泡利门（Pauli Gates）可以通过适当的微波脉冲序列来实现。
双量子比特门： 例如，CNOT门可以通过微波脉冲与离子阱或超导电路中的相互作用来实现。

3.2.8 微波脉冲操控的优势与挑战

优势：

精确控制： 可以实现对量子态的精确操控。
高速操作： 微波脉冲的操作速度可以达到纳秒量级。
可编程性： 可以通过编程实现不同的量子门操作。

挑战：

退相干： 微波脉冲操控过程中，量子态容易受到环境噪声的影响，导致退相干。
校准问题： 微波脉冲的强度、频率和持续时间需要精确校准。
串扰： 多个量子比特之间的微波脉冲可能会相互干扰，导致操作错误。

3.2.9 微波脉冲操控的应用

超导量子计算： 微波脉冲操控是超导量子计算机中实现量子门操作的主要手段。
离子阱量子计算： 微波脉冲也可以用于操控离子阱中的量子态，例如，通过微波脉冲实现离子之间的纠缠。
核磁共振量子计算： 在核磁共振量子计算中，微波脉冲被用来操控核自旋的量子态。

三、量子态制备的挑战与未来

3.2.10 量子态制备的挑战

高保真度： 量子态制备的保真度直接影响量子计算的准确性，需要尽可能减少制备过程中的错误。
可重复性： 量子态制备过程需要具有高度的可重复性，以确保量子计算的可靠性。
可扩展性： 随着量子比特数的增加，量子态制备的复杂性也相应增加，需要开发更有效的制备方法。

3.2.11 未来发展方向

量子态制备的自动化： 开发自动化技术来实现量子态制备过程的自动化和优化。
新型量子态制备方法： 探索新的量子态制备方法，例如，利用量子纠缠态或量子隐形传态来制备量子态。
量子态制备的集成化： 将量子态制备技术与量子纠错技术相结合，实现更强大的量子计算系统。

四、总结

在本节中，我们深入探讨了量子态制备的两种关键技术：

激光冷却： 利用激光来降低原子或离子的动能，是实现超冷原子和离子阱量子计算的关键技术。
微波脉冲操控： 利用微波脉冲来操控量子态，是实现量子门操作的重要手段。

这两种技术展示了人类对微观世界的精确操控能力，为实现高保真度的量子计算奠定了基础。然而，量子态制备仍然面临诸多挑战，需要不断的技术创新和突破。

总而言之，量子态的制备是量子计算实现过程中至关重要的一环，而激光冷却和微波脉冲操控则是实现这一目标的关键工具。希望这段旅程能够加深您对量子态制备技术的理解，并为您的量子计算学习之旅提供一些启示。

3.3 退相干对抗战：T1/T2时间的生死时速

欢迎来到量子计算实现之路的最后一节。在前两节中，我们探讨了实现量子比特的物理载体以及量子态的制备技术。然而，量子计算的实现不仅仅依赖于量子态的制备和控制，更面临着另一个严峻的挑战：退相干（decoherence）。退相干是量子系统与环境相互作用导致量子相干性丧失的过程，它直接影响量子计算的准确性和可靠性。在本节中，我们将深入探讨退相干现象、其对量子计算的影响以及应对退相干的策略，特别是T1（纵向弛豫时间）和T2（横向弛豫时间）这两个关键参数。

一、退相干：量子计算的“隐形敌人”

3.3.1 什么是退相干？

退相干是指量子系统由于与环境相互作用，导致其量子相干性逐渐丧失的过程。具体来说：

量子相干性： 量子态的叠加性和纠缠性是量子计算的核心优势，而量子相干性是维持这些特性的关键。
退相干过程： 量子系统不可避免地与环境发生相互作用，例如，与热库、电磁场、杂质等的相互作用，这些相互作用会导致量子态的相位信息逐渐丢失。

3.3.2 退相干的影响

退相干对量子计算的影响是毁灭性的：

量子态的破坏： 退相干会导致量子态从纯态演化为混合态，破坏量子态的叠加性和纠缠性。
计算错误： 退相干会导致量子门操作出现错误，影响计算结果的准确性。
信息丢失： 退相干最终会导致量子信息的丢失，使得量子计算无法完成。

3.3.3 退相干的来源

热噪声： 环境中的热能会导致量子系统发生非相干跃迁。
电磁场噪声： 电磁场波动会导致量子态的相位发生随机变化。
自发性辐射： 量子系统会自发辐射光子，导致能量损失和相干性丧失。
与其他量子系统的相互作用： 量子系统与其他量子系统（例如，杂质原子、缺陷等）相互作用，会导致量子态的改变。

二、T1 和 T2：衡量退相干的关键参数

3.3.4 T1（纵向弛豫时间）

T1 描述了量子系统能量弛豫的时间尺度，即量子态从高能级向低能级跃迁所需的时间。

定义： T1 是量子系统从激发态回到基态所需的平均时间。
物理意义： T1 反映了量子系统与环境交换能量的速率。
对量子计算的影响： T1 时间越长，量子态的能量信息越稳定，退相干的影响越小。

3.3.5 T2（横向弛豫时间）

T2 描述了量子系统相位弛豫的时间尺度，即量子态的相位信息丧失所需的时间。

定义： T2 是量子态的相干性丧失所需的平均时间。
物理意义： T2 反映了量子系统相位信息的稳定性。
与 T1 的关系： 通常情况下，T2 ≤ 2T1，因为相位信息丧失的速度总是快于能量信息丧失的速度。
对量子计算的影响： T2 时间越长，量子态的相位信息越稳定，量子门操作的保真度越高。

3.3.6 T1 和 T2 的测量

T1 测量： 可以通过测量量子态从激发态回到基态的衰减曲线来获得 T1 时间。
T2 测量： 可以通过测量量子态的拉比振荡或自旋回波（spin echo）来获得 T2 时间。

三、应对退相干的策略

3.3.7 量子纠错码

量子纠错码（Quantum Error Correction Codes）是应对退相干的重要手段：

基本原理： 通过冗余编码，将量子信息编码到多个量子比特上，并利用量子态的纠缠特性来检测和纠正错误。
常见编码： 例如，重复码（Repetition Code）、稳定子码（Stabilizer Code）等。
挑战： 量子纠错码需要消耗大量的量子资源，并且对量子门操作的保真度要求很高。

3.3.8 量子错误缓解

量子错误缓解（Quantum Error Mitigation）是一系列降低量子计算错误率的技术：

动态去耦（Dynamic Decoupling）： 通过施加特定的脉冲序列来抑制环境噪声的影响，延长 T2 时间。
脉冲整形（Pulse Shaping）： 通过优化微波脉冲的形状和参数来减少操作错误。
错误检测与纠正： 在量子电路中嵌入错误检测电路，并在发现错误时采取措施进行纠正。

3.3.9 改进硬件设计

改进硬件设计是提高量子比特相干性的根本途径：

材料优化： 选择更纯净的材料，减少杂质和缺陷对量子态的影响。
封装技术： 改进封装技术，减少环境噪声对量子比特的干扰。
低温技术： 降低量子比特的工作温度，例如，采用稀释制冷机来达到更低的温度。

3.3.10 拓扑量子计算

拓扑量子计算（Topological Quantum Computing）提供了一种从根本上解决退相干问题的方法：

拓扑保护： 拓扑量子比特的量子信息存储在拓扑不变量中，对局部扰动不敏感，具有很强的抗退相干能力。
低错误率： 理论上，拓扑量子比特的错误率可以降低到非常低的水平。

四、总结

在本节中，我们深入探讨了退相干现象及其对量子计算的影响：

退相干： 是量子系统与环境相互作用导致的量子相干性丧失的过程，是量子计算面临的主要挑战之一。
T1 和 T2： 是衡量退相干的关键参数，分别描述了能量弛豫和相位弛豫的时间尺度。
应对策略： 包括量子纠错码、量子错误缓解、改进硬件设计和拓扑量子计算等。

退相干是量子计算发展道路上必须克服的障碍。尽管目前我们还没有找到完美的解决方案，但科学家们正在不断探索新的方法和策略，以期实现更强大的量子计算系统。

总而言之，退相干是量子计算实现过程中的一大挑战，而 T1 和 T2 时间则是衡量退相干程度的重要指标。通过不断的技术创新和突破，我们有理由相信，量子计算的未来将更加光明。希望这段旅程能够加深您对退相干现象的理解，并为您的量子计算学习之旅提供一些启示。

第二部分：量子编程入门篇

第4章量子编程模型

量子电路模型：从经典逻辑门到CNOT门的认知跨越
量子编程语言：Qiskit与Cirq的编程范式对比
量子虚拟机实战：IBM Quantum Experience初探

4.1 量子电路模型：从经典逻辑门到 CNOT 门的认知跨越

欢迎来到量子编程模型的第一节。在本章中，我们将深入探讨量子电路模型，它是量子计算中最基础、最直观的计算模型之一。量子电路模型借鉴了经典计算中电路的概念，但引入了量子力学的独特特性，如叠加性、纠缠性和量子门操作的幺正性。在本节中，我们将从经典逻辑门出发，逐步深入到量子门，特别是CNOT 门，并探讨它们之间的本质区别和联系。

一、经典逻辑门回顾：计算的基础

在深入量子电路之前，让我们先回顾一下经典计算中的逻辑门。

4.1.1 经典逻辑门概述

经典逻辑门是构建数字电路的基本单元，它们对二进制输入进行逻辑运算，并产生二进制输出。常见的经典逻辑门包括：

与门（AND Gate）： 只有当所有输入都为 1 时，输出才为 1。
或门（OR Gate）： 只要有一个输入为 1，输出就为 1。
非门（NOT Gate）： 对输入进行取反操作。
异或门（XOR Gate）： 当两个输入不同时，输出为 1。

4.1.2 经典逻辑门的特性

确定性： 对于给定的输入，经典逻辑门的输出是确定的。
不可逆性： 大多数经典逻辑门操作是不可逆的，例如，与门和或门无法从输出推断出输入。
组合性： 经典逻辑门可以组合起来，实现更复杂的逻辑运算。

4.1.3 经典逻辑门的局限性

经典逻辑门基于布尔代数，只能处理二进制状态（0 和 1），这限制了它们的计算能力。例如，经典计算机无法有效地解决某些指数级复杂性的问题，例如，大整数分解和图着色问题。

二、量子电路模型的基本概念

4.1.4 量子电路模型概述

量子电路模型是量子计算中的一种重要计算模型，它将量子计算过程表示为一系列量子门的组合。

主要特点：

量子比特（qubit）： 量子电路的基本单元是量子比特，它不仅可以处于 0 和 1 的状态，还可以处于它们的叠加态。
量子门（quantum gate）： 量子电路由一系列量子门组成，这些量子门对量子比特进行幺正变换。
量子线路（quantum circuit）： 量子电路可以表示为一系列量子门的组合，形成一个量子线路。

4.1.5 量子电路与经典电路的区别

状态空间： 经典电路的状态空间是离散的，而量子电路的状态空间是连续的。
叠加性： 量子电路可以利用量子叠加态进行并行计算，而经典电路只能处理确定的状态。
纠缠性： 量子电路可以创建和操控量子纠缠态，而经典电路无法实现这种特性。
幺正性： 量子门操作是幺正的，即它们是可逆的，并且保持量子态的内积不变，而经典逻辑门操作通常是不可逆的。

三、从经典逻辑门到量子门：跨越认知的桥梁

4.1.6 经典逻辑门的量子对应物

一些经典逻辑门在量子计算中有对应的量子门：

非门（NOT Gate）： 对应于量子门 X 门（Pauli X Gate），它将 ∣0⟩ 转换为 ∣1⟩，将 ∣1⟩ 转换为∣0⟩。
恒等门（Identity Gate）： 对应于量子门 I 门，它保持量子态不变。
受控非门（Controlled-NOT Gate）： 对应于量子门 CNOT 门，它以第一个量子比特为控制比特，第二个量子比特为目标比特。当控制比特为∣1⟩ 时，对目标比特执行 X 门操作。

4.1.7 量子门的独特性

然而，大多数量子门在经典计算中没有直接的逻辑门：

哈达玛门（Hadamard Gate）： 哈达玛门将量子比特置于叠加态。

将∣0⟩ 转换为。

将∣1⟩ 转换为。

相位门（Phase Gate）： 将∣1⟩ 的相位旋转90°。相位门可以改变量子态的相位信息。
π/8π/8 门（T Gate）： 将∣1⟩ 的相位旋转45°。T 门是实现通用量子计算的重要门。

4.1.8 量子门的组合与量子线路

量子门可以组合起来，形成更复杂的量子线路。例如：

量子傅里叶变换（Quantum Fourier Transform）： 是一系列量子门的组合，用于实现量子态的傅里叶变换。
量子相位估计算法（Quantum Phase Estimation）： 利用量子傅里叶变换来估计量子态的相位。
量子搜索算法（Quantum Search Algorithm）： 例如，Grover 算法，利用量子门操作来加速搜索过程。

四、CNOT 门：量子纠缠的引擎

4.1.9 CNOT 门的定义

CNOT 门（Controlled-NOT Gate）是量子电路中最重要的双量子比特门之一，其定义如下：

控制比特： 第一个量子比特。
目标比特： 第二个量子比特。
操作规则： 当控制比特为∣1⟩ 时，对目标比特执行 X 门操作；否则，保持目标比特不变。

数学表示：

4.1.10 CNOT 门的特性

受控操作： CNOT 门实现了受控非操作，是构建更复杂量子门的基础。
量子纠缠： CNOT 门可以用于创建量子纠缠态。例如，将两个量子比特初始化到∣0⟩ 状态，然后应用哈达玛门和 CNOT 门，可以得到贝尔态：
通用性： CNOT 门与单量子比特门一起，构成了一个通用的量子门集合，可以实现任意量子计算。

4.1.11 CNOT 门的应用

量子纠缠： CNOT 门是创建量子纠缠态的主要工具。
量子纠错： CNOT 门用于实现量子纠错码，例如，重复码和稳定子码。
量子算法： 许多量子算法，例如，量子傅里叶变换和量子相位估计算法，都依赖于 CNOT 门。

五、量子电路模型的局限性

尽管量子电路模型是量子计算的重要工具，但它也存在一些局限性：

噪声和退相干： 量子电路容易受到噪声和退相干的影响，导致量子态的破坏。
可扩展性： 随着量子比特数的增加，量子电路的复杂性也相应增加，需要更有效的量子电路优化技术。
实现难度： 构建大规模的量子电路仍然面临技术挑战，例如，量子门的精确控制和量子比特的连接。

六、总结

在本节中，我们从经典逻辑门出发，逐步深入到量子电路模型，并重点探讨了 CNOT 门的特性：

经典逻辑门： 是经典计算的基础，但存在局限性。
量子电路模型： 借鉴了经典电路的概念，但引入了量子力学的独特特性，例如，叠加性、纠缠性和幺正性。
CNOT 门： 是量子电路中最重要的双量子比特门，是创建量子纠缠态和实现量子计算的关键工具。

量子电路模型为我们理解量子计算的实现方式提供了重要的框架，而 CNOT 门则是量子电路的核心组件。通过学习和掌握量子电路模型，您可以更好地理解量子计算的基本原理，并为未来的量子编程和量子算法设计做好准备。

总而言之，量子电路模型是量子计算的重要组成部分，而 CNOT 门则是其灵魂所在。希望这段旅程能够激发您对量子电路的兴趣，并为您的量子计算学习之旅提供一些启示。

4.2 量子编程语言：Qiskit 与 Cirq 的编程范式对比

欢迎继续深入量子编程模型的世界。在上一节中，我们探讨了量子电路模型，并了解了如何从经典逻辑门过渡到量子门，特别是 CNOT 门。在本节中，我们将把目光转向量子编程语言和框架，重点对比两种主流的量子编程工具：Qiskit 和 Cirq。这两种框架分别由 IBM 和 Google 开发，各自代表了不同的编程范式和设计理念。通过对比，我们将深入了解量子编程的现状，并探索如何选择合适的工具来实现量子算法。

一、Qiskit：模块化与用户友好的典范

4.2.1 Qiskit 概述

Qiskit（Quantum Information Science Kit）是 IBM 开发的一个开源量子计算框架，旨在为量子计算的研究和应用提供全面的工具包。Qiskit 基于 Python 语言，具有以下主要特点：

模块化设计： Qiskit 分为多个子模块，每个模块负责不同的功能。
用户友好性： 提供简洁的 API 和丰富的文档，方便用户快速上手。
与 IBM Quantum Experience 集成： 可以直接提交量子程序到 IBM 的量子硬件上运行。

4.2.2 Qiskit 的模块化结构

Qiskit 的模块化设计是其一大亮点，主要包括以下模块：

Terra（基础模块）： 提供构建、编译和优化量子电路的基本工具。
- QuantumCircuit： 用于构建量子电路的核心类。
- QuantumRegister 和 ClassicalRegister： 用于定义量子比特和经典比特。
- 各种量子门： 例如，HGate, XGate, CNOTGate 等。
Aer（模拟器模块）： 提供高性能的量子电路模拟器。
- QasmSimulator： 模拟量子电路的测量结果。
- StatevectorSimulator： 模拟量子态的演化。
- UnitarySimulator： 模拟量子电路的幺正矩阵。
Ignis（量子纠错模块）： 提供量子纠错和量子错误缓解的工具。
- 量子错误检测与纠正： 例如，重复码、稳定子码等。
- 量子错误缓解技术： 例如，动态去耦、错误缓解算法等。
Aqua（量子算法模块）： 提供各种量子算法的实现。
- 量子傅里叶变换： 实现量子态的傅里叶变换。
- 量子相位估计算法： 估计量子态的相位。
- Grover 搜索算法： 实现量子搜索。
- VQE（变分量子本征求解器）： 用于量子化学计算。

4.2.3 Qiskit 的编程范式

Qiskit 采用面向对象的编程范式，用户可以通过创建对象和调用方法来构建和操作量子电路。

示例代码：

from qiskit import QuantumCircuit, Aer, execute

# 创建量子电路，包含 2 个量子比特和 2 个经典比特
qc = QuantumCircuit(2, 2)

# 应用哈达玛门到第一个量子比特
qc.h(0)

# 应用 CNOT 门，以第一个量子比特为控制比特，第二个量子比特为目标比特
qc.cx(0, 1)

# 添加测量操作
qc.measure([0,1], [0,1])

# 选择模拟器
backend = Aer.get_backend('qasm_simulator')

# 执行量子电路
job = execute(qc, backend, shots=1024)

# 获取结果
result = job.result()
counts = result.get_counts(qc)
print(counts)

4.2.4 Qiskit 的优势

模块化： 不同的功能被封装在不同的模块中，易于管理和扩展。
用户友好： 提供了简洁的 API 和丰富的文档，适合初学者和高级用户。
与硬件集成： 可以直接与 IBM 的量子硬件进行交互，方便进行实际的量子计算实验。
社区支持： 拥有庞大的用户社区和丰富的资源，例如，教程、示例代码和论坛。

二、Cirq：灵活与底层控制的代表

4.2.5 Cirq 概述

Cirq 是 Google 开发的一个开源量子计算框架，旨在为量子计算的研究和开发提供灵活的工具。与 Qiskit 不同，Cirq 更注重对量子电路的底层控制和灵活性。

4.2.6 Cirq 的设计理念

灵活性： 提供更底层的接口，允许用户对量子电路进行更精细的控制。
可扩展性： 设计上考虑了未来量子硬件的发展，支持自定义量子门和量子比特。
与谷歌量子硬件集成： 可以将量子程序提交到谷歌的量子处理器上运行，例如，Sycamore 处理器。

4.2.7 Cirq 的编程范式

Cirq 采用函数式编程和面向对象编程的混合范式，用户可以通过函数和类来构建和操作量子电路。

示例代码：

import cirq

# 创建量子比特
q0, q1 = cirq.LineQubit.range(2)

# 创建量子电路
circuit = cirq.Circuit()
circuit.append(cirq.H(q0))
circuit.append(cirq.CNOT(q0, q1))
circuit.append(cirq.measure(q0, q1))

# 打印量子电路
print(circuit)

# 运行模拟器
simulator = cirq.Simulator()
result = simulator.run(circuit, repetitions=1024)
print(result.histogram(key=[q0, q1]))

4.2.8 Cirq 的优势

灵活性： 提供了更底层的接口，允许用户对量子电路进行更精细的控制，例如，自定义量子门和量子比特。
可扩展性： 设计上考虑了未来量子硬件的发展，支持自定义量子门和量子比特。
与谷歌量子硬件集成： 可以将量子程序提交到谷歌的量子处理器上运行。
性能优化： 提供了高效的量子电路优化和编译工具。

4.2.9 Cirq 的局限性

用户友好性： 对于初学者来说，Cirq 的学习曲线可能比 Qiskit 更陡峭。
社区支持： 与 Qiskit 相比，Cirq 的用户社区和资源相对较少。

三、Qiskit 与 Cirq 的对比

特性	Qiskit	Cirq
编程语言	Python	Python
设计理念	模块化、用户友好	灵活性、底层控制
与硬件集成	与 IBM Quantum Experience 集成	与谷歌量子硬件集成
模拟器	功能强大的 Aer 模拟器	内置模拟器
量子门库	丰富的量子门库	灵活的量子门定义
社区支持	庞大的用户社区和丰富的资源	较新的框架，社区正在发展
文档和教程	丰富的文档和教程	良好的文档，但资源较少
应用领域	量子算法开发、量子模拟、量子机器学习	量子电路设计、量子硬件控制、量子算法实现

4.2.10 如何选择合适的量子编程框架？

选择合适的量子编程框架取决于您的具体需求：

目标平台： 如果您计划使用 IBM 的量子硬件，Qiskit 是更好的选择；如果您计划使用谷歌的量子硬件，Cirq 更为合适。
编程风格： 如果您喜欢模块化设计和用户友好的 API，Qiskit 可能更适合；如果您更倾向于底层控制和灵活性，Cirq 可能更合适。
应用领域： 如果您专注于量子算法开发、量子模拟或量子机器学习，Qiskit 提供了更丰富的工具和资源；如果您更关注量子电路设计和量子硬件控制，Cirq 提供了更灵活的工具。
社区支持： Qiskit 拥有更大的用户社区和更多资源，而 Cirq 作为一个较新的框架，社区正在发展。

四、总结

在本节中，我们深入对比了两种主流的量子编程语言和框架：

Qiskit： 模块化、用户友好，与 IBM Quantum Experience 集成，适合量子算法开发和模拟。
Cirq： 灵活、底层控制，与谷歌量子硬件集成，适合量子电路设计和硬件控制。

这两种框架各有优缺点，选择合适的框架取决于您的具体需求和目标。无论选择哪一种，Qiskit 和 Cirq 都为量子计算的研究和应用提供了强大的工具。

总而言之，量子编程语言和框架是实现量子计算的重要工具，而 Qiskit 和 Cirq 则是其中的佼佼者。通过学习和掌握这些工具，您可以更好地探索量子计算的奥秘，并为未来的量子计算应用做好准备。希望这段旅程能够激发您对量子编程的兴趣，并为您的量子计算学习之旅提供一些启示。

4.3 量子虚拟机实战：IBM Quantum Experience 初探

欢迎来到量子编程模型的最后一节。在前两节中，我们探讨了量子电路模型以及两种主流的量子编程语言和框架：Qiskit 和 Cirq。在本节中，我们将通过IBM Quantum Experience（以下简称 IBM QX）进行一场量子虚拟机实战，带领您亲身体验量子计算的魅力。IBM QX 是一个基于云的量子计算平台，为用户提供了访问量子硬件和模拟器的接口，即使您没有实际的量子硬件，也可以通过它来编写和运行量子程序。

一、IBM Quantum Experience 概述

4.3.1 什么是 IBM Quantum Experience？

IBM Quantum Experience 是 IBM 于 2016 年推出的全球首个基于云的量子计算平台，旨在让全球的研究人员、开发者和爱好者能够访问量子计算资源。该平台提供：

量子硬件访问： 用户可以提交量子程序到 IBM 的量子处理器上运行。
量子模拟器： 提供功能强大的模拟器，用于模拟量子电路的行为。
图形化界面： 提供直观的图形化界面，方便用户构建和运行量子电路。
Qiskit 集成： 与 Qiskit 无缝集成，用户可以使用 Qiskit 编写量子程序并提交到 IBM QX 上运行。

4.3.2 IBM QX 的主要功能

1.量子电路编辑器（Quantum Composer）：提供一个图形化的界面，用户可以通过拖放量子门来构建量子电路。

2.量子模拟器：提供多种模拟器选项，例如，理想模拟器、噪声模拟器等，用于模拟量子电路的行为。

3.量子硬件访问：用户可以提交量子程序到 IBM 的量子处理器上运行，例如，IBM Q System One。

4.Qiskit 集成：用户可以使用 Qiskit 编写量子程序，并通过 IBM QX 的 API 将其提交到云端运行。

5.社区和资源：提供丰富的教程、文档和社区支持，帮助用户学习和使用量子计算。

二、IBM Quantum Experience 实战指南

4.3.3 注册和登录

1.访问 IBM QX 网站：打开浏览器，访问 IBM Quantum Experience。

2.注册账户：如果您还没有账户，点击“Sign Up”按钮，按照提示注册一个 IBM 账户。

3.登录：使用您的 IBM 账户登录 IBM QX。

4.3.4 探索量子电路编辑器

1.进入量子实验室（Quantum Lab）：登录后，点击左侧导航栏中的“Quantum Lab”进入量子实验室。

2.创建新电路：点击“New Circuit”按钮，进入量子电路编辑器。

3. 构建简单电路：

添加量子比特： 默认情况下，电路包含一个量子比特。您可以通过点击“+”按钮添加更多量子比特。
添加量子门： 从左侧的量子门库中拖放量子门到量子比特线上。例如，拖放一个 H 门（哈达玛门）到第一个量子比特上。
添加测量操作： 从量子门库中拖放一个测量门（Measure）到每个量子比特上。

示例电路：

q[0]: ───H───M───

这个电路将一个量子比特初始化到 ∣0⟩∣0⟩ 状态，应用哈达玛门将其置于叠加态，然后进行测量。

4. 运行电路：

选择后端： 在“Backend”下拉菜单中选择一个模拟器，例如，“qasm_simulator”。
运行电路： 点击“Run”按钮，提交电路到模拟器上运行。
查看结果： 等待几秒钟，查看测量结果的概率分布。

预期结果：

{'0': 50, '1': 50}

这表明量子比特处于 0 和 1 的叠加态，测量结果为 0 或 1 的概率各为 50%。

4.3.5 构建更复杂的电路

1. 添加更多量子比特和量子门：

双量子比特电路：
```
q[0]: ───H───@───M───
              │
q[1]: ───────X───M───
```
这个电路将第一个量子比特置于叠加态，然后通过 CNOT 门将其与第二个量子比特纠缠起来，最后进行测量。
预期结果：
```
{'00': 50, '11': 50}
```
这表明两个量子比特处于纠缠态，测量结果为 00 或 11 的概率各为 50%。

2. 运行电路并查看结果：

选择“qasm_simulator”作为后端，运行电路。
查看测量结果的概率分布，验证电路的正确性。

4.3.6 提交量子程序到量子硬件

1. 选择量子硬件后端：

在“Backend”下拉菜单中选择一个可用的量子处理器，例如，“ibmq_bogota”。
注意：量子硬件资源有限，您可能需要排队等待。

2. 提交电路：

点击“Run”按钮，提交电路到量子硬件上运行。
等待一段时间，具体时间取决于队列长度和硬件负载。

3. 查看结果：

量子硬件的结果可能与模拟器结果略有不同，因为量子硬件存在噪声和误差。
比较模拟器结果和硬件结果，分析误差来源。

4.3.7 使用 Qiskit 编写和运行量子程序

1. 安装 Qiskit：

pip install qiskit

2. 编写量子程序：

from qiskit import QuantumCircuit, transpile, assemble, Aer, execute
from qiskit.visualization import plot_histogram

# 创建量子电路
qc = QuantumCircuit(2, 2)
qc.h(0)
qc.cx(0, 1)
qc.measure([0,1], [0,1])

# 选择模拟器
backend = Aer.get_backend('qasm_simulator')

# 运行电路
job = execute(qc, backend, shots=1024)

# 获取结果
result = job.result()
counts = result.get_counts(qc)
print(counts)

# 可视化结果
plot_histogram(counts)

3. 运行量子程序：

运行上述代码，您将看到测量结果的概率分布，并生成一个直方图。

4. 将量子程序提交到 IBM QX：

from qiskit import IBMQ

# 加载 IBM QX 账户
IBMQ.load_account()

# 选择后端
provider = IBMQ.get_provider(hub='ibm-q')
backend = provider.get_backend('ibmq_bogota')

# 运行电路
job = execute(qc, backend, shots=1024)

# 获取结果
result = job.result()
counts = result.get_counts(qc)
print(counts)

这段代码将您的量子程序提交到 IBM QX 上的指定量子处理器上运行，并返回测量结果。

三、总结

在本节中，我们通过 IBM Quantum Experience 进行了一场量子虚拟机实战：

IBM QX 概述： 提供了访问量子硬件和模拟器的接口，是学习和探索量子计算的重要工具。
实战指南： 带领您一步步构建和运行量子电路，包括简单电路和更复杂的纠缠电路。
Qiskit 集成： 展示了如何使用 Qiskit 编写量子程序，并将其提交到 IBM QX 上运行。

通过 IBM QX，您可以亲身体验量子计算的魅力，并探索量子算法的实际应用。无论您是量子计算的研究者、开发者，还是对量子计算感兴趣的爱好者，IBM QX 都是一个理想的平台。

总而言之，IBM Quantum Experience 是开启量子计算之旅的钥匙，它为我们提供了一个强大的工具来探索量子计算的奥秘。希望这段旅程能够激发您对量子计算的热情，并为您的量子计算学习之旅提供一些启示。

第5章基本量子算法

Deutsch-Jozsa算法：量子并行性的首次惊艳亮相
量子傅里叶变换：相位估计算法的交响乐指挥
振幅放大原理：Grover搜索的几何旋转艺术

5.1 Deutsch-Jozsa算法：量子并行性的首次惊艳亮相

欢迎来到量子算法世界的大门。在本章中，我们将深入探讨量子计算史上第一个具有里程碑意义的算法——Deutsch-Jozsa算法。这个算法不仅展示了量子计算的强大潜力，还首次揭示了量子并行性的惊人威力。让我们一同踏上这段探索之旅，了解这个算法如何通过量子力学的独特特性，实现了经典计算无法企及的速度提升。

一、背景与动机：经典计算的限制

在深入探讨Deutsch-Jozsa算法之前，我们需要了解它所要解决的问题，以及经典计算在解决这些问题时的局限性。

5.1.1 布尔函数分类问题

Deutsch-Jozsa算法旨在解决以下问题：

问题描述： 给定一个函数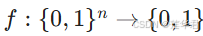，该函数保证是常数函数或平衡函数。
- 常数函数： 对所有输入，函数值都相同，即 f(x)=0 或 f(x)=1 对所有 x 成立。
- 平衡函数： 一半输入的函数值为 0，另一半为 1。
目标： 确定给定的函数是常数函数还是平衡函数。

5.1.2 经典算法的局限性

在经典计算中，解决这个问题需要以下步骤：

1.查询函数：对不同的输入 x 查询函数 f(x)。

2.统计结果：统计函数值为 0 和 1 的输入数量。

3.判断函数类型：如果所有查询结果相同，则函数是常数函数；否则，是平衡函数。

经典算法的复杂度：

最坏情况： 需要查询次才能确定函数的类型。
- 例如，对于 n=2，需要查询 3 次。
- 对于 n=10，需要查询 513 次。
平均情况： 需要查询次。

这意味着，随着输入规模的增加，经典算法所需的查询次数呈指数级增长。

二、Deutsch-Jozsa算法的诞生

1992年，大卫·杜奇（David Deutsch）和理查德·乔萨（Richard Jozsa）提出了Deutsch-Jozsa算法，这是第一个证明量子计算在解决某些特定问题上具有指数级优势的算法。

5.1.3 算法思想

Deutsch-Jozsa算法的核心思想是利用量子力学的叠加性和量子并行性：

叠加性： 量子比特可以处于多个状态的叠加态。
量子并行性： 通过对叠加态进行操作，量子计算机可以同时处理所有可能的输入。

5.1.4 算法步骤

1. 量子比特初始化：

准备 n+1 个量子比特，将前 nn 个量子比特初始化到∣0⟩ 状态，最后一个量子比特初始化到∣1⟩ 状态。
状态表示为：

2. 应用哈达玛门：

对所有 n+1 个量子比特应用哈达玛门（Hadamard gate）。
哈达玛门将∣0⟩ 转换为，将∣1⟩ 转换为。
状态变为：

3. 应用量子黑盒函数  :

是一个量子黑盒，它对输入状态∣x⟩⊗∣y⟩ 进行如下操作：

其中，⊕ 表示按位异或。
应用后，状态变为：

4. 再次应用哈达玛门：

对前 n 个量子比特再次应用哈达玛门。
状态变为：

其中，表示 x 和 y 的点积。

5. 测量前 n 个量子比特：

测量前 n 个量子比特。
如果函数是常数函数，则测量结果为 0^n （即，所有比特都为 0）。
如果函数是平衡函数，则测量结果不会是 0^n。

5.1.5 算法分析

正确性： 上述步骤可以正确判断函数是常数函数还是平衡函数。
复杂度： 算法只需要对量子黑盒函数进行一次查询，而经典算法则需要指数次查询。
量子优势： Deutsch-Jozsa算法展示了量子计算在解决特定问题上具有指数级的速度提升。

三、量子并行性的体现

Deutsch-Jozsa算法是量子并行性的典型例子：

叠加态： 通过对量子比特应用哈达玛门，算法将输入状态制备成叠加态，使得所有可能的输入 xx 同时被处理。
量子黑盒函数： 量子黑盒函数对叠加态进行操作，相当于同时对所有输入 x 计算 f(x)。
干涉效应： 再次应用哈达玛门后，干涉效应使得常数函数和平衡函数产生不同的测量结果。

这种利用叠加态和干涉效应的方法，使得 Deutsch-Jozsa 算法能够以指数级的速度解决经典计算难以解决的问题。

四、Deutsch-Jozsa算法的意义

开创性： Deutsch-Jozsa算法是第一个证明量子计算优势的算法，为后续量子算法的发展奠定了基础。
量子并行性的展示： 该算法展示了量子并行性的强大威力，启发了许多其他量子算法的设计。
理论基础： 为量子计算的理论研究提供了重要的案例，证明了量子计算在某些问题上具有超越经典计算的潜力。

五、总结

在本节中，我们深入探讨了 Deutsch-Jozsa 算法：

问题背景： 经典计算在解决布尔函数分类问题上存在指数级的复杂度瓶颈。
算法思想： 利用量子叠加性和量子并行性，通过一次查询即可确定函数的类型。
算法步骤： 详细介绍了算法的实现步骤，包括量子比特初始化、哈达玛门应用、量子黑盒函数应用等。
量子并行性的体现： 展示了量子并行性如何使算法实现指数级的速度提升。
意义： 证明了量子计算的优势，并为量子计算的发展开辟了道路。

Deutsch-Jozsa 算法是量子计算史上的一个重要里程碑，它不仅展示了量子计算的强大潜力，还为后续的量子算法研究提供了宝贵的思路。希望这段旅程能够激发您对量子算法的兴趣，并为您的量子计算学习之旅提供一些启示。

5.2 量子傅里叶变换：相位估计算法的交响乐指挥

欢迎继续深入量子算法的奇妙世界。在上一节中，我们探讨了Deutsch-Jozsa算法，它展示了量子计算在解决特定问题上相对于经典计算的指数级优势。在本节中，我们将深入探讨另一个至关重要的量子算法——量子傅里叶变换（Quantum Fourier Transform, QFT），它是许多其他量子算法的基石，特别是相位估计算法。量子傅里叶变换可以被视为量子计算中的“交响乐指挥”，它协调着量子态的相位信息，为解决复杂问题提供了强大的工具。

一、经典傅里叶变换回顾

在深入量子傅里叶变换之前，让我们先回顾一下经典傅里叶变换。

5.2.1 经典傅里叶变换概述

经典傅里叶变换（Discrete Fourier Transform, DFT）是一种将时域信号转换为频域信号的数学工具。其定义如下：

其中：

是时域信号的第 j 个样本。
是频域信号的第 k 个频率分量。
是信号的长度。

5.2.2 经典傅里叶变换的应用

经典傅里叶变换在信号处理、图像处理、音频分析等领域有着广泛的应用，例如：

频谱分析： 分析信号的频率成分。
滤波： 去除或增强特定频率的信号成分。
数据压缩： 通过去除冗余频率成分来压缩数据。

二、量子傅里叶变换的定义与特性

5.2.3 量子傅里叶变换的定义

量子傅里叶变换是经典傅里叶变换的量子版本，其定义如下：

其中：

∣j⟩ 是输入量子态，表示二进制数 j。
∣k⟩ 是输出量子态，表示二进制数 k。
N = 2^n，其中 n 是量子比特的数量。

5.2.4 量子傅里叶变换的特性

幺正性： 量子傅里叶变换是一个幺正变换，这意味着它是一个可逆的线性变换，并且保持量子态的内积不变。
指数级加速： 量子傅里叶变换可以利用量子并行性，在 O(n^2) 时间内完成，而经典傅里叶变换需要 O(NlogN) 时间。对于 n 个量子比特，N=2^n，因此量子傅里叶变换实现了指数级的加速。
相位信息的利用： 量子傅里叶变换对量子态的相位信息进行操作，这是其区别于经典傅里叶变换的关键。

5.2.5 量子傅里叶变换的电路实现

量子傅里叶变换可以通过一系列量子门操作来实现，主要包括：

1.哈达玛门（Hadamard Gate）：对每个量子比特应用哈达玛门。

2.受控相位门（Controlled Phase Gate）：对不同量子比特对应用受控相位门，旋转角度取决于量子比特的索引。

3.交换门（SWAP Gate）：对量子比特进行重新排序。

示例电路：

对于 3 个量子比特，量子傅里叶变换的电路可以表示为

q[0]: ───H───P(π/2)───P(π/4)───@───SWAP───
                                 │         │
q[1]: ───────H───P(π/2)───@───────X───────
                           │               │
q[2]: ───────────H───P(π/2)───X─────────────

其中：

H 表示哈达玛门。
P(θ) 表示相位门，旋转角度为 θ。
@ 表示受控相位门。
X 表示 NOT 门。
SWAP 表示交换门。

三、相位估计算法：量子傅里叶变换的应用

5.2.6 相位估计算法概述

相位估计算法（Quantum Phase Estimation, QPE）是利用量子傅里叶变换来估计量子态的相位信息的一种算法。其主要应用包括：

特征值估计： 估计酉矩阵的特征值。
量子模拟： 模拟量子系统的演化。
Shor算法： 分解大整数，是量子计算的重要应用之一。

5.2.7 相位估计算法的步骤

1. 量子态准备：

准备一个包含 nn 个辅助量子比特的量子态 ∣0⟩⊗n∣0⟩⊗n，以及一个包含 mm 个量子比特的量子态 ∣ψ⟩∣ψ⟩，其中 ∣ψ⟩∣ψ⟩ 是待估计相位的量子态。
状态表示为：

2. 应用哈达玛门：

对辅助量子比特应用哈达玛门。
状态变为：

3. 应用受控酉变换：

对每个辅助量子比特应用受控酉变换 U2kU2k，其中 UU 是待估计相位的酉矩阵。
状态变为：

由于，因此：

状态可以表示为：

4. 应用量子傅里叶变换：

对辅助量子比特应用量子傅里叶变换。
状态变为：

5. 测量辅助量子比特：

测量辅助量子比特，得到测量结果 j 。
通过对 j 进行经典计算，可以估计相位 ϕ 。

5.2.8 相位估计算法的应用

Shor算法： 相位估计算法是 Shor 算法的重要组成部分，用于估计周期，从而实现大整数分解。
量子模拟： 相位估计算法可以用于估计量子系统的能量本征值。
量子化学计算： 相位估计算法可以用于计算分子的基态能量。

四、量子傅里叶变换的意义

核心变换： 量子傅里叶变换是许多量子算法的核心组件，例如，相位估计算法、Shor 算法等。
指数级加速： 量子傅里叶变换实现了对经典傅里叶变换的指数级加速，是量子计算优势的重要体现。
量子态操控： 量子傅里叶变换对量子态的相位信息进行操控，为量子计算提供了强大的工具。

五、总结

在本节中，我们深入探讨了量子傅里叶变换：

定义与特性： 量子傅里叶变换是经典傅里叶变换的量子版本，具有幺正性、指数级加速和相位信息操控等特性。
电路实现： 详细介绍了量子傅里叶变换的电路实现，包括哈达玛门、受控相位门和交换门等。
相位估计算法： 展示了量子傅里叶变换在相位估计算法中的应用，以及其在量子计算中的重要性。
意义： 量子傅里叶变换是量子计算的核心变换，是实现许多量子算法的基础。

量子傅里叶变换是量子计算中不可或缺的工具，它为解决复杂问题提供了强大的数学手段。通过学习和掌握量子傅里叶变换，您可以更好地理解量子算法的设计原理，并为未来的量子计算应用做好准备。

总而言之，量子傅里叶变换是量子计算交响乐的指挥家，它协调着量子态的相位信息，为量子计算的实现和发展提供了重要的支持。希望这段旅程能够激发您对量子算法的兴趣，并为您的量子计算学习之旅提供一些启示。

5.3 振幅放大原理：Grover搜索的几何旋转艺术

欢迎来到量子算法世界的最后一节。在前两节中，我们探讨了Deutsch-Jozsa算法和量子傅里叶变换，它们展示了量子计算在解决特定问题上的强大潜力。在本节中，我们将深入探讨另一个具有里程碑意义的量子算法——Grover搜索算法，以及其背后的核心原理——振幅放大原理。Grover算法不仅在理论上具有重要意义，还在实践中展示了量子计算在解决搜索问题上的优势。让我们一同揭开这个算法的神秘面纱，探索其几何旋转的艺术。

一、经典搜索问题与Grover算法的提出

5.3.1 经典搜索问题

在经典计算中，搜索问题是一个基本问题：

问题描述： 给定一个无序数据库，包含 N 个元素，其中只有一个目标元素满足特定条件（例如，目标元素的值为 1，其他元素值为 0）。
目标： 找到目标元素。

5.3.2 经典算法的局限性

在经典计算中，解决这个问题需要以下步骤：

1.线性搜索：从数据库的第一个元素开始，逐个检查每个元素，直到找到目标元素。

2.复杂度：平均需要 O(N) 次查询，最坏情况下需要 N 次查询。

这意味着，随着数据库规模的增加，经典算法所需的查询次数线性增长。

5.3.3 Grover算法的提出

1996年，洛夫·格罗弗（Lov Grover）提出了Grover搜索算法，该算法利用量子力学的特性，在无序数据库中以的时间复杂度找到目标元素，实现了平方加速。

二、振幅放大原理：Grover算法的核心

5.3.4 振幅放大的概念

振幅放大（Amplitude Amplification）是Grover算法的核心思想，其基本思想是：

量子态的振幅： 量子态的每个基态都有一个对应的振幅，振幅的平方表示测量到该基态的概率。
目标： 增大目标状态的振幅，同时减小非目标状态的振幅，从而提高测量到目标状态的可能性。

5.3.5 Grover迭代：振幅放大的实现

Grover算法通过一系列迭代操作来实现振幅放大，每个迭代包括两个主要步骤：

1.相位翻转（Oracle）：对目标状态应用一个相位翻转操作，将目标状态的相位翻转 180∘180∘。

2.平均翻转（Diffusion Operator）：对所有状态应用一个平均翻转操作，将所有状态的振幅关于平均值进行翻转。

5.3.6 Grover迭代的数学描述

假设初始状态为：

其中，N=2^n，n 是量子比特的数量。

相位翻转（Oracle）：

定义一个量子黑盒函数 f(x)，当 x 是目标状态时，f(x)=1；否则，f(x)=0。
对量子态应用一个酉变换：

这意味着，目标状态的相位被翻转 180∘180∘，而其他状态的相位保持不变。

平均翻转（Diffusion Operator）：

定义一个扩散算符：

其中，是单位矩阵。
对量子态应用：

这意味着，所有状态的振幅关于平均值进行翻转。

5.3.7 Grover迭代的几何解释

Grover迭代的几何解释可以更好地理解振幅放大的过程：

状态空间： 量子态可以看作是一个高维空间中的向量。
初始状态： 初始状态是所有基态的等概率叠加。
目标状态： 目标状态是我们想要找到的状态。
迭代过程：

1.相位翻转：将目标状态的相位翻转180°，相当于将向量关于超平面 H 反射。

2.平均翻转：将所有状态的振幅关于平均值进行翻转，相当于将向量关于初始状态反射。
迭代效果： 每次迭代都会使目标状态的振幅增大，而非目标状态的振幅减小。经过次迭代后，目标状态的振幅达到最大值。

5.3.8 Grover算法的步骤

1. 量子比特初始化： 将 n 个量子比特初始化到∣0⟩ 状态。

2. 应用哈达玛门： 对所有量子比特应用哈达玛门，将初始状态制备成等概率叠加态：

3. Grover迭代： 重复以下步骤 k 次：

相位翻转： 对目标状态应用相位翻转操作。
平均翻转： 对所有状态应用平均翻转操作。

其中，。

4.测量：对量子比特进行测量，得到目标状态。

5.3.9 Grover算法的复杂度

时间复杂度：，实现了对经典线性搜索的平方加速。
空间复杂度：。

三、Grover算法的应用与局限性

5.3.10 应用

数据库搜索： 在无序数据库中搜索目标元素。
组合优化： 解决组合优化问题，例如，旅行商问题。
量子模拟： 在量子模拟中寻找特定量子态。

5.3.11 局限性

无序性： Grover算法假设数据库是无序的。如果数据库有序，可以利用经典算法实现更快的搜索。
重复元素： 如果数据库中存在多个目标元素，Grover算法的性能会下降。
量子资源： 实现Grover算法需要大量的量子资源，例如，量子比特和量子门操作。

四、总结

在本节中，我们深入探讨了Grover搜索算法：

问题背景： 经典搜索问题在无序数据库中需要线性时间复杂度。
振幅放大原理： 解释了Grover算法的核心思想，即通过相位翻转和平均翻转来放大目标状态的振幅。
Grover迭代： 详细介绍了Grover迭代的几何解释和数学描述。
算法步骤： 描述了Grover算法的实现步骤，包括量子比特初始化、哈达玛门应用、Grover迭代和测量等。
应用与局限性： 讨论了Grover算法的应用领域和局限性。

Grover算法是量子计算中最重要的算法之一，它展示了量子计算在解决搜索问题上的强大优势。通过学习和掌握Grover算法，您可以更好地理解量子计算的实际应用，并为未来的量子计算研究提供重要的参考。

总而言之，振幅放大原理是Grover算法的灵魂，它通过几何旋转的艺术，实现了量子态的振幅放大，为量子搜索开辟了新的道路。希望这段旅程能够激发您对量子算法的兴趣，并为您的量子计算学习之旅提供一些启示。

第6章量子纠错入门

表面编码：拓扑量子计算的保护伞
稳定子码解析：泡利矩阵的纠错密码
容错阈值定理：量子可靠性的生死线

6.1 表面编码：拓扑量子计算的保护伞

欢迎来到量子纠错的世界。在前面的章节中，我们探讨了量子计算的基本原理、量子算法以及量子编程模型。然而，量子计算的实现面临着巨大的挑战，其中最严峻的挑战之一就是退相干（decoherence）和量子错误（quantum errors）。为了克服这些挑战，科学家们提出了量子纠错（quantum error correction）技术。在本章中，我们将深入探讨量子纠错领域的一个重要概念——表面编码（Surface Code），它被广泛认为是实现容错量子计算最有前途的方法之一。让我们一同揭开表面编码的神秘面纱，了解其如何利用拓扑学原理来保护量子信息。

一、量子纠错的必要性

在深入探讨表面编码之前，我们需要了解量子纠错的必要性。

6.1.1 量子退相干与错误

退相干： 量子系统不可避免地与环境相互作用，导致量子相干性逐渐丧失，最终导致量子态的破坏。
量子错误： 退相干会导致各种类型的量子错误，例如：
- 比特翻转错误（Bit-flip Error）：∣0⟩ ↔ ∣1⟩。
- 相位翻转错误（Phase-flip Error）： ，其中，。
- 更复杂的错误： 例如，X, Y, Z 错误（泡利错误）。

6.1.2 量子纠错的需求

错误率： 量子门操作和量子比特的错误率远高于经典计算。例如，超导量子比特的错误率通常在 $10^{-3}$ 到 $10^{-2}$ 量级。
容错计算： 为了实现可靠的量子计算，需要将错误率降低到可接受的水平（例如， $10^{-15}$ 或更低）。
量子纠错码： 量子纠错码是实现容错量子计算的关键工具，它们可以检测和纠正量子错误。

二、表面编码的基本概念

6.1.3 什么是表面编码？

表面编码（Surface Code）是一种基于拓扑量子纠错原理的量子纠错码。它利用二维量子比特阵列中的拓扑特性来保护量子信息。

主要特点：

二维结构： 表面编码使用一个二维的量子比特阵列，通常是正方形或六边形的格子。
物理量子比特与逻辑量子比特： 表面编码将多个物理量子比特组合起来，形成一个逻辑量子比特。
拓扑保护： 表面编码利用拓扑学原理，使得量子信息对局部错误具有很强的免疫力。

6.1.4 表面编码的编码方式

数据量子比特（Data Qubits）： 位于格子的顶点，用于存储量子信息。
测量量子比特（Measure Qubits）： 位于格子的边或面上，用于检测错误。
稳定子（Stabilizer）： 表面编码使用稳定子来定义逻辑量子比特的状态。稳定子是一组相互对易的厄米算符，其本征值为 +1。

6.1.5 表面编码的错误检测

表面编码通过以下步骤来检测错误：

1.测量稳定子：对每个稳定子进行测量，得到测量结果。

2.错误综合征：通过分析测量结果，可以推断出错误的发生位置和类型。

3.错误纠正：根据错误综合征结果，应用相应的纠正操作。

6.1.6 表面编码的优势

高容错阈值： 表面编码具有较高的容错阈值（例如，~1%），这意味着即使量子门的错误率较高，也可以实现容错量子计算。
可扩展性： 表面编码的结构简单，易于扩展到大量量子比特。
与现有技术兼容： 表面编码可以利用现有的量子硬件技术实现，例如，超导电路和离子阱。

6.1.7 表面编码的局限性

资源消耗大： 表面编码需要大量的物理量子比特来实现一个逻辑量子比特。例如，实现一个容错逻辑量子比特可能需要数百个物理量子比特。
操作复杂度高： 表面编码的操作（例如，错误检测和纠正）相对复杂，需要精确的控制和协调。
二维限制： 表面编码主要基于二维结构，可能限制了其未来的扩展性。

三、表面编码的工作原理

6.1.8 稳定子测量

表面编码的核心是稳定子测量：

Z 型稳定子： 对每个 plaquette（由四个数据量子比特包围的区域）进行测量，得到 Z 型稳定子测量值。
X 型稳定子： 对每个 star（由四个数据量子比特相交的点）进行测量，得到 X 型稳定子测量值。

6.1.9 错误检测

通过分析稳定子测量值，可以检测出错误：

Z 型错误： 导致 Z 型稳定子测量值发生变化。
X 型错误： 导致 X 型稳定子测量值发生变化。
Y 型错误： 同时影响 X 型和 Z 型稳定子测量值。

6.1.10 错误纠正

根据错误检测结果，应用相应的纠正操作：

Z 型错误纠正： 对相应的数据量子比特应用 Z 门。
X 型错误纠正： 对相应的数据量子比特应用 X 门。
Y 型错误纠正： 对相应的数据量子比特应用 Y 门。

6.1.11 逻辑操作

表面编码不仅可以检测和纠正错误，还可以实现逻辑量子门操作：

逻辑 X 门： 对一行数据量子比特应用 X 门。
逻辑 Z 门： 对一列数据量子比特应用 Z 门。
逻辑 CNOT 门： 通过一系列复杂的操作实现。

四、表面编码的应用

6.1.12 拓扑量子计算

表面编码是实现拓扑量子计算的重要工具：

拓扑量子比特： 表面编码将量子信息存储在拓扑不变量中，具有很强的抗干扰能力。
容错量子计算： 表面编码为实现容错量子计算提供了可行的方案。

6.1.13 量子模拟与量子化学计算

表面编码可以用于构建大型量子模拟器和量子计算机，用于模拟复杂的量子系统，例如，分子结构和化学反应。

6.1.14 量子通信

表面编码可以用于实现更可靠的量子通信协议，例如，量子密钥分发和量子隐形传态。

五、总结

在本节中，我们深入探讨了表面编码：

基本概念： 表面编码是一种基于拓扑量子纠错原理的量子纠错码。
编码方式： 利用二维量子比特阵列中的稳定子来定义逻辑量子比特。
错误检测与纠正： 通过测量稳定子来检测错误，并应用相应的纠正操作。
优势： 高容错阈值、可扩展性强、与现有技术兼容。
应用： 拓扑量子计算、量子模拟、量子通信等。

表面编码是量子纠错领域的一项重要技术，它为实现容错量子计算提供了可行的方案。通过学习和掌握表面编码，您可以更好地理解量子纠错的基本原理，并为未来的量子计算研究提供重要的参考。

总而言之，表面编码是量子计算的“保护伞”，它利用拓扑学原理，为量子信息提供了强大的保护。希望这段旅程能够激发您对量子纠错的兴趣，并为您的量子计算学习之旅提供一些启示。

6.2 稳定子码解析：泡利矩阵的纠错密码

欢迎继续深入量子纠错的世界。在上一节中，我们探讨了表面编码，它利用拓扑学原理来保护量子信息，是实现容错量子计算的重要工具。在本节中，我们将深入探讨量子纠错领域另一个至关重要的概念——稳定子码（Stabilizer Code），特别是其与泡利矩阵（Pauli Matrices）的密切关系。稳定子码不仅为量子纠错提供了一个强大的数学框架，还揭示了量子纠错与经典纠错之间的深刻联系。让我们一同揭开稳定子码的神秘面纱，探索其背后的纠错密码。

一、经典纠错码回顾

在深入稳定子码之前，让我们先回顾一下经典纠错码的基本概念。

6.2.1 经典纠错码概述

经典纠错码用于检测和纠正数据传输或存储过程中出现的错误。常见的经典纠错码包括：

汉明码（Hamming Code）： 能够纠正单个比特错误。
里德-所罗门码（Reed-Solomon Code）： 能够纠正多个比特错误，广泛应用于 CD、DVD 和 QR 码中。
卷积码（Convolutional Code）： 适用于连续数据流，广泛应用于无线通信中。

6.2.2 经典纠错码的基本原理

冗余编码： 通过添加冗余比特来增加信息的冗余度。
错误检测： 利用冗余信息检测错误的发生。
错误纠正： 利用冗余信息和纠错算法纠正错误。

二、稳定子码的基本概念

6.2.3 什么是稳定子码？

稳定子码是一类重要的量子纠错码，其定义基于一组相互对易的厄米算符，称为稳定子（stabilizers）。稳定子码利用稳定子来定义量子码字空间，并检测和纠正量子错误。

6.2.4 稳定子的定义

稳定子： 一个厄米算符 SS 被称为稳定子，如果它满足以下条件：

对于所有码字。
稳定子群： 一组相互对易的稳定子构成一个群，称为稳定子群。

6.2.5 稳定子码的编码方式

码字空间： 稳定子码的码字空间由所有满足稳定子条件的量子态组成，即：

其中，Si 是稳定子群中的稳定子。
逻辑量子比特： 稳定子码将多个物理量子比特组合起来，形成一个逻辑量子比特。

6.2.6 稳定子码与泡利矩阵的关系

泡利矩阵是量子力学中描述自旋-1/2 粒子的基本算符，包括：

X 矩阵（泡利 X 矩阵）： 对应于比特翻转错误。
Z 矩阵（泡利 Z 矩阵）： 对应于相位翻转错误。
Y 矩阵（泡利 Y 矩阵）： 对应于同时发生比特翻转和相位翻转错误。

稳定子码的稳定子通常由泡利矩阵的乘积构成。例如：

X 型稳定子： 由多个 X 矩阵的乘积构成。
Z 型稳定子： 由多个 Z 矩阵的乘积构成。

6.2.7 稳定子码的错误检测

稳定子码通过测量稳定子来检测错误：

错误检测： 如果某个稳定子的测量值发生变化，则说明发生了错误。
错误综合征： 通过分析哪些稳定子的测量值发生了变化，可以推断出错误的发生位置和类型。

6.2.8 稳定子码的错误纠正

根据错误检测结果，应用相应的纠正操作：

X 型错误： 对相应的量子比特应用 X 门。
Z 型错误： 对相应的量子比特应用 Z 门。
Y 型错误： 对相应的量子比特应用 Y 门。

三、稳定子码的优势

6.2.9 高效的错误检测与纠正

稳定子码利用稳定子群的结构，可以高效地检测和纠正量子错误：

线性性： 稳定子码的错误检测和纠正过程是线性的，易于实现。
可扩展性： 稳定子码可以扩展到大量量子比特，适用于构建大型量子纠错码。

6.2.10 与经典纠错码的联系

稳定子码与经典线性码有着深刻的联系：

经典对应物： 每个稳定子码都有一个对应的经典线性码。
经典-量子对应： 稳定子码的错误检测和纠正过程可以看作是经典线性码在量子领域的推广。

6.2.11 丰富的编码构造方法

稳定子码的构造方法非常丰富，例如：

CSS 码（Calderbank-Shor-Steane Code）： 结合了经典线性码和量子纠错码的优点。
拓扑码： 例如，表面编码和色码，利用拓扑学原理来实现量子纠错。

四、稳定子码的应用

6.2.12 表面编码

表面编码是稳定子码的一个重要例子，它利用二维量子比特阵列中的稳定子来实现量子纠错。

6.2.13 量子计算

稳定子码是实现容错量子计算的关键工具：

量子门操作： 稳定子码可以用于实现容错的量子门操作。
量子算法： 许多量子算法，例如，Shor 算法和 Grover 算法，都需要稳定的量子纠错机制。

6.2.14 量子通信

稳定子码可以用于实现更可靠的量子通信协议：

量子密钥分发： 稳定子码可以用于检测和纠正量子密钥分发过程中的错误。
量子隐形传态： 稳定子码可以用于实现更可靠的量子隐形传态。

五、总结

在本节中，我们深入探讨了稳定子码：

基本概念： 稳定子码是一类基于稳定子群的量子纠错码。
与泡利矩阵的关系： 稳定子通常由泡利矩阵的乘积构成。
错误检测与纠正： 通过测量稳定子来检测错误，并应用相应的纠正操作。
优势： 高效的错误检测与纠正、与经典纠错码的联系、丰富的编码构造方法。
应用： 表面编码、量子计算、量子通信等。

稳定子码是量子纠错领域的一个重要工具，它为实现容错量子计算提供了强大的数学框架。通过学习和掌握稳定子码，您可以更好地理解量子纠错的基本原理，并为未来的量子计算研究提供重要的参考。

总而言之，稳定子码是量子纠错的“密码”，它利用泡利矩阵的数学结构，为量子信息提供了可靠的保护。希望这段旅程能够激发您对量子纠错的兴趣，并为您的量子计算学习之旅提供一些启示。

6.3 容错阈值定理：量子可靠性的生死线

欢迎来到量子纠错章节的最后一节。在前两节中，我们探讨了表面编码和稳定子码，这些技术为量子纠错提供了重要的理论框架和实现方法。然而，量子纠错的有效性最终取决于一个关键因素：容错阈值（Fault-tolerant Threshold）。在本节中，我们将深入探讨容错阈值定理，它揭示了量子计算能否走向实用化的关键条件。让我们一同深入理解这个定理，探讨其对量子计算未来发展的深远影响。

一、量子计算的可靠性挑战

在深入探讨容错阈值定理之前，我们需要了解量子计算面临的可靠性挑战。

6.3.1 量子错误的来源

量子计算系统中的错误来源主要包括：

退相干： 量子系统与环境相互作用，导致量子相干性丧失。
门操作错误： 量子门操作（例如，哈达玛门、CNOT 门等）存在固有错误。
测量错误： 量子测量过程存在误差。
初始化错误： 量子比特的初始化过程存在误差。

6.3.2 量子错误的累积效应

错误传播： 量子错误会随着量子门的操作而传播和累积。
错误率： 随着量子电路深度的增加，错误率呈指数级增长。
可靠性瓶颈： 量子计算的可靠性受到错误率的严重限制。

6.3.3 经典纠错的局限性

经典纠错方法无法直接应用于量子计算：

不可克隆定理： 量子态不能被完美复制，这使得经典纠错中常用的冗余编码方法难以直接应用。
测量干扰： 对量子态的测量会不可避免地改变其状态，这使得经典纠错中常用的错误检测方法难以直接应用。

二、容错量子计算的概念

为了克服上述挑战，科学家们提出了容错量子计算（Fault-tolerant Quantum Computing）的概念。

6.3.4 容错量子计算的定义

容错量子计算是指在存在错误的情况下，仍然能够可靠地执行量子计算的技术。其核心思想是：

错误检测与纠正： 通过量子纠错码来检测和纠正量子错误。
容错操作： 设计容错的量子门操作，使得即使在存在错误的情况下，量子计算仍然能够正确进行。

6.3.5 容错量子计算的关键要素

量子纠错码： 例如，表面编码和稳定子码，用于保护量子信息。
容错量子门： 例如，容错的 CNOT 门和单量子比特门，用于实现可靠的量子操作。
量子错误检测与纠正协议： 例如，重复测量和纠错操作，用于处理检测到的错误。

三、容错阈值定理

6.3.6 定理的提出

1996年，约翰·普雷斯基尔（John Preskill）提出了容错阈值定理，该定理为量子计算的可靠性提供了理论依据。

6.3.7 定理的内容

容错阈值定理可以表述如下：

存在一个阈值： 对于给定的量子纠错码和量子门操作，存在一个错误率阈值 pthpth。
低于阈值： 如果每个量子门的错误率低于 pth，并且量子纠错码能够有效地纠正错误，那么量子计算就可以以任意高的可靠性进行。
高于阈值： 如果错误率高于 pth，则量子计算的可靠性将迅速下降，无法实现可靠的量子计算。

6.3.8 定理的物理意义

生死线： 容错阈值 pth 可以看作是量子计算的“生死线”。只有当错误率低于这个阈值时，量子计算才有可能实现。
可扩展性： 容错阈值定理表明，只要错误率足够低，量子计算就可以通过增加量子比特数量来实现可扩展性。

6.3.9 阈值估计

不同的量子纠错码和量子门操作方案具有不同的容错阈值：

表面编码： 理论估计的容错阈值约为 1%。
稳定子码： 不同的稳定子码具有不同的容错阈值，例如，Steane 码的阈值约为 0.75%。
实际实现： 由于实际量子硬件中存在各种非理想因素，实际的容错阈值通常低于理论估计值。

四、实现容错量子计算的挑战

6.3.10 低错误率的要求

硬件改进： 为了达到容错阈值，需要大幅降低量子门的错误率。这需要对量子硬件进行持续改进，例如，提高量子比特的相干时间、减少噪声和退相干等。
量子纠错码优化： 需要开发更高效的量子纠错码和错误检测与纠正协议，以降低资源消耗和提高纠错效率。

6.3.11 资源消耗

物理量子比特： 实现一个逻辑量子比特需要大量的物理量子比特。例如，表面编码需要数百个物理量子比特来实现一个逻辑量子比特。
量子门操作： 容错量子计算需要更多的量子门操作来执行纠错和容错操作，这增加了量子电路的复杂性和资源消耗。

6.3.12 量子硬件的集成与控制

大规模集成： 构建大规模的量子纠错系统需要将大量的量子比特和量子门集成在一起，并实现精确的控制和协调。
量子控制技术： 需要开发更先进的量子控制技术，以实现对量子比特的精确操控和测量。

五、容错量子计算的进展与展望

6.3.13 实验进展

近年来，科学家们在实现容错量子计算方面取得了重要进展：

表面编码实验： 一些实验已经实现了小规模的表面编码，并成功检测和纠正了量子错误。
量子纠错码优化： 研究人员正在开发更高效的量子纠错码，例如，色码（Color Code）和拓扑量子码（Topological Quantum Code）。
量子硬件改进： 量子硬件技术正在不断进步，例如，超导电路、离子阱和拓扑量子比特的错误率正在逐渐降低。

6.3.14 未来展望

突破容错阈值： 未来，随着量子硬件技术的进步和量子纠错码的优化，突破容错阈值将成为可能。
实现容错量子计算： 一旦突破容错阈值，量子计算将进入一个新的时代，量子计算机将能够可靠地执行复杂的量子算法。
量子计算的广泛应用： 容错量子计算的实现将推动量子计算在密码学、材料科学、药物设计、人工智能等领域的广泛应用。

六、总结

在本节中，我们深入探讨了容错阈值定理：

量子计算的可靠性挑战： 量子错误是量子计算面临的主要挑战。
容错量子计算的概念： 通过量子纠错码和容错操作来实现可靠的量子计算。
容错阈值定理： 揭示了量子计算能否实现的关键条件，即错误率必须低于容错阈值。
实现容错量子计算的挑战： 包括低错误率的要求、资源消耗和量子硬件的集成与控制。
进展与展望： 近年来取得了重要进展，未来突破容错阈值和实现容错量子计算充满希望。

容错阈值定理是量子计算发展道路上的一个重要里程碑，它为量子计算的可靠性提供了理论依据，并为实现容错量子计算指明了方向。希望这段旅程能够加深您对量子纠错的理解，并为您的量子计算学习之旅提供一些启示。

第三部分：量子算法进阶篇

第7章量子算法三巨头

Shor算法详解：周期查找与RSA加密的量子葬礼
HHL算法革命：线性方程组的量子加速奥秘
量子行走理论：图论问题的新型解决范式

7.1 Shor算法详解：周期查找与RSA加密的量子葬礼

欢迎来到量子算法三巨头的第一章。在本章中，我们将深入探讨Shor算法，它无疑是量子计算领域最具影响力的算法之一。Shor算法由彼得·肖尔（Peter Shor）于1994年提出，它展示了量子计算在解决某些特定问题上相对于经典计算的指数级优势，特别是整数分解问题。这一突破不仅在理论上有重要意义，还对现有的RSA加密系统构成了巨大威胁。让我们一同深入了解Shor算法的原理、步骤及其对密码学的深远影响。

一、背景与动机：RSA加密与整数分解问题

在深入探讨Shor算法之前，我们需要了解它所要解决的问题，以及这个问题对经典密码学的重要性。

7.1.1 RSA加密概述

RSA（Rivest-Shamir-Adleman）加密是一种广泛使用的公钥加密算法，其安全性基于以下数学难题：

整数分解问题： 给定两个大素数 p 和 q，计算它们的乘积 N=p×q 是容易的；但给定 N，分解出 p 和 q 是极其困难的。

7.1.2 RSA加密的安全性

公钥和私钥： RSA加密使用一对密钥，公钥用于加密，私钥用于解密。
安全性假设： RSA的安全性依赖于整数分解问题的计算难度。如果能够有效地分解大整数，那么RSA加密就会被破解。

7.1.3 经典算法的局限性

在经典计算中，解决整数分解问题的主要算法包括：

试除法： 最简单的方法，但效率极低，对于大整数几乎不可行。
Pollard's Rho 算法： 适用于中等大小的整数，但无法处理非常大的整数。
数域筛法（Number Field Sieve）： 目前最有效的经典整数分解算法，但其时间复杂度仍然是亚指数级的，即，其中 c 是常数。

这意味着，随着整数位数的增加，经典算法所需的计算时间呈指数级增长。

二、Shor算法的核心思想

Shor算法的核心思想是利用量子力学的特性，特别是量子傅里叶变换，来有效地解决整数分解问题。其基本思路是：

周期查找： 将整数分解问题转化为周期查找问题。
量子傅里叶变换： 利用量子傅里叶变换来加速周期查找过程。

7.1.4 周期查找问题

给定一个函数，其中 a 是与 N 互素的整数，Shor算法旨在找到该函数的周期 r，即满足：

7.1.5 周期查找与整数分解的关系

一旦找到周期 r，可以通过以下步骤来分解 N：

三、Shor算法的步骤

Shor算法可以分为以下几个主要步骤：

7.1.6 量子态准备

1. 初始化： 准备 n 个量子比特，将其初始化到 ∣0⟩ 状态。

2. 应用哈达玛门： 对所有 nn 个量子比特应用哈达玛门，将其制备成等概率叠加态：

7.1.7 量子黑盒函数应用

1. 定义量子黑盒函数： 定义一个量子黑盒函数 UfUf，它对输入状态 ∣x⟩⊗∣0⟩∣x⟩⊗∣0⟩ 进行如下操作：

其中，。

2. 应用：对量子态应用：

7.1.8 量子傅里叶变换

1. 应用量子傅里叶变换： 对前 nn 个量子比特应用量子傅里叶变换：

7.1.9 测量与经典计算

1.测量前 n 个量子比特：测量前 n 个量子比特，得到测量结果 k。

2.经典计算：对 k 进行经典计算，例如，计算其连分数展开，以估计周期 r。

7.1.10 周期验证

1.验证周期：检查 r 是否为 f(x) 的周期。

2.重复实验：如果 r 不是周期，则重复上述步骤，直到找到正确的周期。

7.1.11 整数分解

四、Shor算法的优势与挑战

7.1.12 优势

指数级加速： Shor算法能够在多项式时间内解决整数分解问题，而经典算法需要亚指数时间。
对RSA加密的威胁： Shor算法对RSA加密构成了巨大威胁，因为RSA的安全性依赖于整数分解问题的困难性。

7.1.13 挑战

量子资源需求： 实现 Shor 算法需要大量的量子比特和量子门操作。
量子纠错： Shor算法对量子错误非常敏感，需要强大的量子纠错机制。
硬件实现： 目前的量子硬件技术还无法实现大规模的 Shor 算法。

五、Shor算法的意义

密码学革命： Shor算法对现有的公钥加密系统，例如，RSA、ECC（椭圆曲线加密）等，构成了巨大威胁，迫使人们寻找新的加密方法。
量子计算的优势： Shor算法展示了量子计算在解决某些特定问题上相对于经典计算的指数级优势。
量子计算发展的推动力： Shor算法的提出极大地推动了量子计算的发展，激励着科学家们探索新的量子算法和量子硬件技术。

六、总结

在本节中，我们深入探讨了 Shor 算法：

问题背景： RSA 加密的安全性依赖于整数分解问题的困难性。
算法思想： 利用量子傅里叶变换来加速周期查找过程，从而实现整数分解。
算法步骤： 详细介绍了 Shor 算法的实现步骤，包括量子态准备、量子黑盒函数应用、量子傅里叶变换、测量与经典计算等。
优势与挑战： 分析了 Shor 算法的优势，例如，指数级加速，以及面临的挑战，例如，量子资源需求和硬件实现。
意义： Shor 算法对密码学产生了深远影响，并推动了量子计算的发展。

Shor 算法是量子计算发展史上的一个重要里程碑，它不仅展示了量子计算的优势，还对现有的密码学体系构成了巨大挑战。希望这段旅程能够激发您对量子算法的兴趣，并为您的量子计算学习之旅提供一些启示。

7.2 HHL算法革命：线性方程组的量子加速奥秘

欢迎来到量子算法三巨头的第二章。在本章中，我们将深入探讨HHL算法，这是由阿伦·阿维达（Aram Harrow）、阿维纳什·哈里（Avinash Hall）和赛斯·劳埃德（Seth Lloyd）在2009年提出的一个革命性算法。HHL算法展示了量子计算在解决线性方程组问题上的强大潜力，其速度相对于经典算法实现了指数级的提升。这一突破不仅在理论上有重要意义，还在科学计算、工程、金融等领域具有广泛的应用前景。让我们一同深入了解HHL算法的原理、步骤及其对计算科学的深远影响。

一、背景与动机：线性方程组的挑战

在深入探讨HHL算法之前，我们需要了解它所要解决的问题，以及这个问题在科学计算中的重要性。

7.2.1 线性方程组概述

线性方程组是科学计算中最基本、最常见的问题之一，其一般形式为：

$Ax=b$

其中：

A 是一个 $N * N$ 的矩阵。
x 是未知向量。
b 是已知向量。

7.2.2 经典算法的局限性

在经典计算中，解决线性方程组的主要方法包括：

高斯消元法： 时间复杂度为。
共轭梯度法： 对于稀疏矩阵，时间复杂度为，其中 κ 是矩阵 A 的条件数。
迭代法： 例如，雅可比迭代、高斯-赛德尔迭代等，时间复杂度取决于矩阵的性质和迭代次数。

对于大规模线性方程组，经典算法的计算成本非常高，尤其是当矩阵 A 非常大或条件数 κ 很大时。

7.2.3 量子计算的优势

量子计算在解决线性方程组问题上的优势主要体现在：

指数级加速： HHL算法能够在某些情况下以指数级的速度解决线性方程组。
量子并行性： 量子计算可以利用叠加态同时处理多个向量，从而实现并行计算。

二、HHL算法的核心思想

HHL算法的核心思想是利用量子相位估计算法来估计矩阵 AA 的特征值，并利用这些特征值来构造解向量 x。

7.2.4 算法思想

特征值估计： 对矩阵 A 进行量子相位估计，得到其特征值。
构造解向量： 利用特征值和向量 b 的量子态来构造解向量 x 的量子态。
振幅放大： 利用振幅放大技术来放大解向量的振幅，从而提高测量到解向量的概率。

三、HHL算法的步骤

HHL算法可以分为以下几个主要步骤：

7.2.5 量子态准备

1.初始化：准备 n 个量子比特，将其初始化到 ∣0⟩ 状态。

2. 编码向量 b： 将向量 b 编码到量子态 ∣b⟩ 中：

其中，N=2^n。

7.2.6 量子相位估计

1. 定义酉矩阵： 定义一个酉矩阵，其中 tt 是一个合适的参数。

2. 应用量子相位估计算法： 对量子态 ∣b⟩ 和辅助量子比特应用量子相位估计算法，得到：

其中，λj 是矩阵 A 的特征值，∣uj⟩ 是对应的特征向量，βj 是向量 b 在特征向量基下的展开系数。

7.2.7 构造解向量

1. 应用条件相位门： 对每个特征值 λjλj，应用一个条件相位门，其中是的函数。

2. 构造解向量： 通过选择合适的，可以将解向量 x 的量子态表示为：

7.2.8 振幅放大

1.应用振幅放大技术：对量子态 ∣x⟩ 应用振幅放大技术，放大解向量的振幅。

2.测量：对量子态进行测量，得到解向量 x 的近似值。

7.2.9 经典后处理

误差分析： 分析测量结果的误差，并进行必要的经典后处理，例如，重采样或迭代改进。

四、HHL算法的优势与挑战

7.2.10 优势

指数级加速： 在某些情况下，HHL算法能够以指数级的速度解决线性方程组。
量子并行性： 利用量子并行性，可以同时处理多个向量。
适用范围广： HHL算法可以应用于各种线性方程组，包括稀疏矩阵和稠密矩阵。

7.2.11 挑战

量子资源需求： 实现 HHL 算法需要大量的量子比特和量子门操作。
条件数依赖性： HHL算法的性能依赖于矩阵 AA 的条件数 κκ。对于条件数很大的矩阵，算法的效率会降低。
量子态提取： HHL算法输出的是解向量的量子态，而不是经典向量。需要额外的步骤来提取经典信息，这可能会引入额外的误差和复杂性。
误差控制： 量子相位估计和振幅放大过程中的误差会影响最终结果的精度，需要有效的误差控制机制。

五、HHL算法的应用

线性代数计算： 例如，求解大规模线性方程组、矩阵求逆等。
科学计算： 例如，量子化学计算、量子模拟等。
工程应用： 例如，电路分析、结构分析等。
金融建模： 例如，期权定价、风险分析等。

六、总结

在本节中，我们深入探讨了 HHL 算法：

问题背景： 线性方程组是科学计算中的基本问题，经典算法在处理大规模问题时面临挑战。
算法思想： 利用量子相位估计和振幅放大技术来构造解向量的量子态。
算法步骤： 详细介绍了 HHL 算法的实现步骤，包括量子态准备、量子相位估计、构造解向量、振幅放大和经典后处理等。
优势与挑战： 分析了 HHL 算法的优势，例如，指数级加速，以及面临的挑战，例如，量子资源需求和误差控制。
应用： HHL 算法在科学计算、工程、金融等领域具有广泛的应用前景。

HHL 算法是量子计算发展史上的一个重要里程碑，它展示了量子计算在解决线性方程组问题上的强大潜力，并为量子计算在科学计算领域的应用开辟了新的道路。希望这段旅程能够激发您对量子算法的兴趣，并为您的量子计算学习之旅提供一些启示。

7.3 量子行走理论：图论问题的新型解决范式

欢迎来到量子算法三巨头的最后一章。在本章中，我们将深入探讨量子行走理论（Quantum Walk Theory），这是一个新兴的量子计算领域，它为解决图论问题和许多其他计算问题提供了一种全新的范式。量子行走是经典随机行走的量子对应物，但它利用了量子力学的独特特性，例如叠加性、干涉性和纠缠性，从而实现了超越经典算法的性能提升。让我们一同深入了解量子行走的原理、应用及其对图论问题解决的革命性影响。

一、经典随机行走回顾

在深入探讨量子行走之前，我们需要先回顾一下经典随机行走的基本概念。

7.3.1 经典随机行走概述

经典随机行走（Classical Random Walk）是一个描述粒子在空间中随机移动的数学模型：

离散时间随机行走： 粒子在离散的时间步长中移动，每次移动的方向是随机的。
连续时间随机行走： 粒子的移动是连续的，时间是连续的。

7.3.2 经典随机行走的应用

经典随机行走广泛应用于：

物理学： 模拟分子运动、布朗运动等。
计算机科学： 随机算法、图遍历、随机搜索等。
金融学： 股票价格模型、期权定价等。

二、量子行走的定义与特性

7.3.3 什么是量子行走？

量子行走（Quantum Walk）是经典随机行走在量子力学框架下的推广。与经典随机行走不同，量子行走利用了量子力学的叠加性、干涉性和纠缠性。

7.3.4 量子行走的类型

离散时间量子行走（Discrete-Time Quantum Walk）： 粒子在离散的时间步长中移动，每次移动由一个幺正算符描述。
连续时间量子行走（Continuous-Time Quantum Walk）： 粒子的移动是连续的，时间是连续的，由一个哈密顿量描述。

7.3.5 量子行走的特性

叠加性： 量子行走中的粒子可以同时处于多个位置的状态。
干涉性： 量子行走的演化过程中，不同路径的量子态会发生干涉，导致概率幅的增强或减弱。
纠缠性： 在多粒子量子行走中，粒子之间可以形成纠缠态。

7.3.6 量子行走与经典随机行走的区别

概率分布： 经典随机行走的概率分布通常是扩散的，而量子行走的概率分布可以表现出干涉效应，导致非经典的概率分布。
速度： 量子行走可以比经典随机行走更快地遍历图结构。
可逆性： 量子行走是幺正变换，因此是可逆的，而经典随机行走是不可逆的。

三、量子行走在图论中的应用

7.3.7 图遍历

量子行走可以用于更有效地遍历图结构：

快速遍历： 量子行走可以利用叠加性和干涉性，在更短的时间内遍历图的所有节点。
搜索算法： 例如，量子行走搜索算法可以在图中更有效地搜索目标节点。

7.3.8 量子行走搜索算法

量子行走搜索算法是 Grover 搜索算法在图结构上的推广：

算法思想： 利用量子行走来探索图结构，并通过振幅放大技术来放大目标节点的振幅。
优势： 相对于经典算法，量子行走搜索算法在某些图结构上可以实现更快的搜索速度。

7.3.9 量子行走与图论问题

量子行走可以用于解决各种图论问题，例如：

最短路径问题： 量子行走可以用于寻找图中两个节点之间的最短路径。
连通游走问题： 量子行走可以用于判断图中两个节点是否连通。
图同构问题： 量子行走可以用于检测图同构。

四、量子行走的优势与挑战

7.3.10 优势

速度优势： 量子行走可以利用量子力学的特性，在某些情况下实现比经典算法更快的计算速度。
并行性： 量子行走可以同时探索多个路径，从而实现并行计算。
非经典特性： 量子行走可以表现出非经典的概率分布和干涉效应，为解决某些问题提供了新的思路。

7.3.11 挑战

实现难度： 量子行走的实现需要精确的量子控制和高保真度的量子门操作。
退相干： 量子行走容易受到退相干的影响，导致量子态的破坏。
算法设计： 设计有效的量子行走算法需要深入理解量子力学和图论知识。

五、量子行走的应用前景

量子算法设计： 量子行走为设计新的量子算法提供了新的工具，例如，量子游走算法、量子随机游走算法等。
量子模拟： 量子行走可以用于模拟量子系统的演化，例如，量子漫步、量子扩散等。
量子计算的其他领域： 量子行走可以应用于量子计算的其他领域，例如，量子密码学、量子机器学习等。

六、总结

在本节中，我们深入探讨了量子行走理论：

定义与特性： 量子行走是经典随机行走在量子力学框架下的推广，具有叠加性、干涉性和纠缠性等特性。
与经典随机行走的区别： 量子行走表现出非经典的概率分布和干涉效应，速度更快，可逆性更强。
图论应用： 量子行走可以用于图遍历、搜索算法、最短路径问题、连通游走问题等。
优势与挑战： 量子行走具有速度优势和并行性，但也面临着实现难度、退相干和算法设计等挑战。
应用前景： 量子行走为量子算法设计、量子模拟和其他量子计算领域提供了新的思路和方法。

量子行走理论是量子计算领域的一颗新星，它为解决图论问题和许多其他计算问题提供了一种全新的范式。通过学习和掌握量子行走，您可以更好地理解量子计算的前沿发展，并为未来的量子计算研究提供重要的参考。

总而言之，量子行走是量子计算的重要组成部分，它利用量子力学的独特特性，为我们提供了一种超越经典算法的新型解决范式。希望这段旅程能够激发您对量子计算的热情，并为您的量子计算学习之旅提供一些启示。

第8章量子机器学习

量子神经网络：参数化量子电路的梯度下降法
量子核方法：希尔伯特空间的特征映射革命
量子强化学习：决策过程的叠加态优化

8.1 量子神经网络：参数化量子电路的梯度下降法

欢迎来到量子机器学习的世界。在本章中，我们将深入探讨量子神经网络（Quantum Neural Networks, QNNs），这是一个新兴的研究领域，旨在将量子计算与深度学习相结合，以期实现超越经典神经网络的性能。量子神经网络利用参数化量子电路（Parameterized Quantum Circuits, PQCs）作为其基本构建模块，并通过梯度下降法等优化技术进行训练。在本节中，我们将详细探讨量子神经网络的原理、结构、训练方法及其潜在应用。

一、量子神经网络的背景与动机

8.1.1 经典神经网络的局限性

经典神经网络在图像识别、自然语言处理等领域取得了巨大成功，但其发展也面临着一些挑战：

计算复杂度： 训练深度神经网络需要大量的计算资源和时间。
数据需求： 深度学习模型通常需要大量标注数据才能取得良好的性能。
可解释性： 深度神经网络的决策过程通常难以解释。

8.1.2 量子计算的优势

量子计算具有以下潜在优势，可以弥补经典神经网络的不足：

指数级并行性： 量子计算可以利用叠加态同时处理大量数据。
量子纠缠： 量子纠缠可以创建复杂的非线性关系。
量子隧穿效应： 量子隧穿效应可以帮助优化算法跳出局部最优解。

8.1.3 量子神经网络的提出

量子神经网络的概念最早可以追溯到20世纪90年代，但随着量子计算技术的进步，近年来才取得了实质性进展。量子神经网络旨在利用量子计算的独特特性来增强或替代经典神经网络。

二、量子神经网络的基本概念

8.1.4 什么是量子神经网络？

量子神经网络是一种利用量子力学原理构建的神经网络，其基本构建模块是参数化量子电路。量子神经网络可以看作是经典神经网络在量子领域的推广。

8.1.5 参数化量子电路（PQC）

参数化量子电路是量子神经网络的核心组件，其结构类似于经典神经网络中的层：

量子比特： PQC 由一组量子比特组成。
参数化量子门： PQC 包含一系列参数化量子门（例如，旋转门），其旋转角度由可训练的参数控制。
测量： 对量子比特进行测量，将量子态转换为经典输出。

8.1.6 量子神经网络的结构

量子神经网络的结构可以多种多样，以下是几种常见的结构：

浅层量子神经网络： 由少量参数化量子门组成，类似于经典神经网络中的浅层网络。
深度量子神经网络： 由多层参数化量子门组成，类似于经典神经网络中的深度网络。
混合量子-经典神经网络： 结合了量子层和经典层，例如，量子层用于特征提取，经典层用于分类或回归。

8.1.7 量子神经网络的示例

一个简单的量子神经网络可以表示为：

1.量子比特初始化：将 n 个量子比特初始化到 ∣0⟩ 状态。

2.参数化量子门层：对每个量子比特应用参数化旋转门（例如，），其中是可训练的参数。

3.纠缠层：应用 CNOT 门或其他纠缠门，在量子比特之间创建纠缠。

4.重复参数化量子门层和纠缠层：重复上述步骤，构建更深的量子电路。

5.测量：对量子比特进行测量，得到经典输出。

三、量子神经网络的训练

8.1.8 梯度下降法

量子神经网络的训练通常采用梯度下降法，其基本思想是：

损失函数： 定义一个损失函数（例如，均方误差、交叉熵等）来衡量量子神经网络的输出与目标值之间的差异。
梯度计算： 计算损失函数关于参数的梯度。
参数更新： 根据梯度信息更新参数，使得损失函数最小化。

8.1.9 参数化量子电路的梯度计算

由于量子电路的幺正性和量子态的叠加性，参数化量子电路的梯度计算与经典神经网络有所不同：

参数移位规则（Parameter Shift Rule）： 一种常用的方法，通过对参数进行微小的偏移来计算梯度。
有限差分法： 通过对参数进行微小的扰动来近似计算梯度。
自动微分： 利用量子计算框架（例如，Qiskit）提供的自动微分工具来计算梯度。

8.1.10 训练过程

1.初始化参数：随机初始化量子神经网络的参数。

2.前向传播：将输入数据编码到量子态中，通过参数化量子电路进行处理，并进行测量，得到输出。

3.计算损失：计算损失函数的值。

4.反向传播：计算损失函数关于参数的梯度。

5.参数更新：根据梯度信息更新参数。

6.重复迭代：重复上述步骤，直到损失函数收敛或达到预定的迭代次数。

四、量子神经网络的挑战

退相干和噪声： 量子神经网络容易受到退相干和噪声的影响，导致量子态的破坏和计算结果的误差。
可训练参数数量： 量子神经网络的参数化量子门数量有限，如何有效地利用这些参数来表达复杂的函数是一个挑战。
训练算法： 量子神经网络的训练算法需要适应量子计算的特性，例如，量子态的叠加性和幺正性。
硬件限制： 目前的量子硬件技术还无法实现大规模的量子神经网络，需要克服硬件限制。

五、量子神经网络的潜在应用

量子化学计算： 量子神经网络可以用于模拟分子结构和化学反应。
量子机器学习： 量子神经网络可以用于构建量子版本的机器学习模型，例如，量子分类器、量子回归模型等。
量子优化： 量子神经网络可以用于解决组合优化问题，例如，旅行商问题、图着色问题等。
量子控制： 量子神经网络可以用于量子系统的控制，例如，量子门的校准和量子态的制备。

六、总结

在本节中，我们深入探讨了量子神经网络：

背景与动机： 量子神经网络旨在结合量子计算和深度学习的优势，解决经典神经网络面临的挑战。
基本概念： 量子神经网络的核心组件是参数化量子电路，其结构类似于经典神经网络。
训练方法： 量子神经网络的训练通常采用梯度下降法，但需要考虑量子计算的特性。
挑战： 退相干、噪声、可训练参数数量、训练算法和硬件限制是量子神经网络面临的主要挑战。
应用： 量子神经网络在量子化学、量子机器学习、量子优化和量子控制等领域具有潜在应用。

量子神经网络是量子计算与机器学习交叉领域的前沿研究方向，它为解决复杂问题提供了新的思路和方法。通过学习和掌握量子神经网络，您可以更好地理解量子计算与机器学习的融合发展，并为未来的量子计算研究提供重要的参考。

总而言之，量子神经网络是量子计算的重要组成部分，它融合了量子计算和深度学习的优势，为我们提供了一种全新的计算范式。希望这段旅程能够激发您对量子机器学习的兴趣，并为您的量子计算学习之旅提供一些启示。

8.2 量子核方法：希尔伯特空间的特征映射革命

欢迎继续深入量子机器学习的世界。在上一节中，我们探讨了量子神经网络，它利用参数化量子电路和梯度下降法，将量子计算与深度学习相结合。在本节中，我们将深入探讨另一种新兴的量子机器学习范式——量子核方法（Quantum Kernel Methods）。量子核方法利用量子力学的独特特性，特别是希尔伯特空间（Hilbert Space）中的特征映射，为机器学习任务提供了全新的视角和强大的工具。让我们一同揭开量子核方法的神秘面纱，探索其在机器学习领域的革命性潜力。

一、经典核方法回顾

在深入探讨量子核方法之前，我们需要先回顾一下经典核方法的基本概念。

8.2.1 经典核方法概述

经典核方法是一类重要的机器学习算法，其核心思想是通过核函数（Kernel Function）将数据映射到高维特征空间，从而实现线性可分的分类或回归。

常见的经典核函数包括：

线性核：
多项式核：
径向基函数核（RBF）：

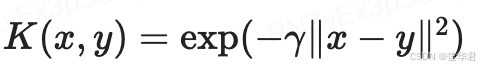
8.2.2 核技巧（Kernel Trick）

核技巧是经典核方法的核心，它允许我们在不显式计算高维特征映射的情况下，利用核函数计算高维空间中的内积：

其中，是数据点 x 的特征映射。

8.2.3 经典核方法的应用

经典核方法广泛应用于：

支持向量机（SVM）： 利用核技巧实现非线性分类。
核主成分分析（Kernel PCA）： 利用核技巧进行非线性降维。
高斯过程回归： 利用核函数进行非线性回归。

二、量子核方法的基本概念

8.2.4 什么是量子核方法？

量子核方法是将经典核方法的思想推广到量子计算领域的一种方法。其核心思想是利用量子态的希尔伯特空间作为特征空间，并通过量子电路来实现特征映射。

8.2.5 量子核函数

量子核函数（Quantum Kernel Function）是量子核方法的核心组件，它定义了在希尔伯特空间中的内积：

其中：

是数据点的量子态表示。
是数据点的量子态表示。

8.2.6 量子特征映射

量子特征映射（Quantum Feature Map）是将经典数据映射到量子态的过程：

量子特征映射可以通过参数化量子电路来实现：

1.数据编码：将经典数据 xx 编码到量子态的初始参数中，例如，使用角度编码（Angle Encoding）或振幅编码（Amplitude Encoding）。

2.量子电路演化：通过参数化量子电路对量子态进行演化，得到最终的量子态。

8.2.7 量子核方法的优势

高维特征空间： 量子态的希尔伯特空间具有极高的维度，甚至可以是无限维的，这使得量子核方法能够捕捉到更复杂的非线性关系。
量子纠缠： 量子纠缠可以创建数据点之间更复杂的关联。
量子干涉： 量子干涉效应可以增强或减弱某些特征，从而提高模型的表达能力。

三、量子核方法的实现

8.2.8 量子核矩阵的计算

量子核矩阵（Quantum Kernel Matrix）是量子核方法的关键，其元素为量子核函数的值：

计算量子核矩阵的过程包括：

1.量子态制备：对每个数据点，制备相应的量子态。

2.内积计算：利用量子电路计算量子态之间的内积。

3.测量：对量子电路进行测量，得到内积的估计值。

8.2.9 量子核支持向量机（Quantum Kernel SVM）

量子核支持向量机是量子核方法的一个典型应用，其步骤如下：

1.计算量子核矩阵：对训练数据计算量子核矩阵。

2.训练 SVM 模型：使用量子核矩阵训练 SVM 模型。

3.预测：对新数据点进行预测，利用量子核函数计算其与支持向量的内积。

8.2.10 量子核主成分分析（Quantum Kernel PCA）

量子核主成分分析是另一种量子核方法的应用，其步骤如下：

1.计算量子核矩阵：对数据计算量子核矩阵。

2.特征值分解：对量子核矩阵进行特征值分解。

3.降维：选择主要特征值对应的特征向量，实现数据降维。

四、量子核方法的挑战

量子资源需求： 计算量子核矩阵需要大量的量子比特和量子门操作。
噪声和退相干： 量子核方法容易受到噪声和退相干的影响，导致计算结果的误差。
数据编码： 选择合适的数据编码方式对于量子核方法的效果至关重要。
可解释性： 量子核方法的结果通常难以解释，需要开发新的解释方法。

五、量子核方法的潜在应用

模式识别： 例如，图像识别、语音识别等。
生物信息学： 例如，蛋白质结构预测、基因数据分析等。
化学和材料科学： 例如，分子性质预测、材料设计等。
金融数据分析： 例如，股票价格预测、风险分析等。

六、总结

在本节中，我们深入探讨了量子核方法：

背景与动机： 量子核方法旨在利用量子力学的特性来增强经典核方法。
基本概念： 量子核方法的核心是量子核函数和量子特征映射。
实现方法： 详细介绍了量子核矩阵的计算以及量子核 SVM 和量子核 PCA 的实现步骤。
优势与挑战： 量子核方法具有高维特征空间和量子纠缠等优势，但也面临着量子资源需求、噪声和退相干等挑战。
应用： 量子核方法在模式识别、生物信息学、化学和材料科学以及金融数据分析等领域具有潜在应用。

量子核方法是量子计算与机器学习交叉领域的又一重要研究方向，它为解决复杂问题提供了新的思路和方法。通过学习和掌握量子核方法，您可以更好地理解量子计算在机器学习中的应用，并为未来的量子计算研究提供重要的参考。

总而言之，量子核方法是量子计算的重要组成部分，它利用希尔伯特空间的特征映射，为我们提供了一种全新的机器学习范式。希望这段旅程能够激发您对量子机器学习的兴趣，并为您的量子计算学习之旅提供一些启示。

8.3 量子强化学习：决策过程的叠加态优化

欢迎来到量子机器学习章节的最后一节。在前两节中，我们探讨了量子神经网络和量子核方法，它们展示了量子计算在机器学习领域的创新应用。在本节中，我们将深入探讨另一个令人兴奋的领域——量子强化学习（Quantum Reinforcement Learning, QRL）。量子强化学习结合了量子计算和强化学习的优势，旨在通过量子力学的独特特性，例如叠加态和纠缠性，来优化决策过程。让我们一同深入了解量子强化学习的原理、方法和潜在应用。

一、强化学习回顾

在深入探讨量子强化学习之前，我们需要先回顾一下经典强化学习的基本概念。

8.3.1 强化学习概述

强化学习（Reinforcement Learning, RL）是一种机器学习方法，智能体（agent）通过与环境的交互来学习如何做出最优决策。其基本要素包括：

智能体（Agent）： 做出决策并执行动作的实体。
环境（Environment）： 智能体与之交互的外部系统。
状态（State）： 环境的当前情况。
动作（Action）： 智能体可以采取的行为。
奖励（Reward）： 智能体执行动作后获得的反馈信号，用于评估动作的好坏。

8.3.2 强化学习的目标

强化学习的目标是学习一个策略（Policy），即从状态到动作的映射，使得智能体在长期内获得最大的累积奖励。

8.3.3 经典强化学习算法

常见的经典强化学习算法包括：

Q 学习（Q-Learning）： 一种基于值函数的学习算法，通过迭代更新 Q 值函数来学习最优策略。
深度 Q 网络（Deep Q-Network, DQN）： 将深度学习与 Q 学习相结合，利用神经网络来近似 Q 值函数。
策略梯度方法（Policy Gradient Methods）： 直接优化策略函数，例如，REINFORCE 算法。

二、量子强化学习的基本概念

8.3.4 什么是量子强化学习？

量子强化学习是将量子计算与强化学习相结合的一种方法。其核心思想是利用量子力学的特性，例如叠加态、纠缠性和量子干涉，来加速强化学习过程或提高其性能。

8.3.5 量子强化学习的主要研究方向

量子态表示： 利用量子态来表示强化学习中的状态、动作或策略。
量子计算加速： 利用量子算法来加速强化学习中的关键步骤，例如，值函数估计、策略优化等。
量子纠缠与协作： 利用量子纠缠来实现智能体之间的协作学习。

三、量子强化学习的方法

8.3.6 量子态表示

状态量子化： 将经典状态空间离散化，并用量子比特来表示不同的状态。
量子态编码： 利用量子态的叠加性来表示多个状态。例如，一个量子比特可以同时表示多个状态：

其中，α 和 β 是复数，满足。
量子纠缠： 利用量子纠缠来表示状态之间的复杂关系。例如，两个量子比特可以处于纠缠态：

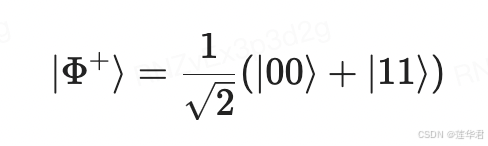
这意味着两个量子比特的状态是相互关联的。

8.3.7 量子计算加速

量子相位估计算法： 可以用于加速值函数估计过程。
量子线性代数算法： 例如，HHL 算法，可以用于加速线性方程组的求解，这在强化学习中具有应用价值。
量子优化算法： 例如，量子近似优化算法（QAOA），可以用于优化策略函数。

8.3.8 量子纠缠与协作

多智能体量子强化学习： 利用量子纠缠来实现多个智能体之间的协作学习。例如，智能体之间的量子态可以处于纠缠态，从而实现更有效的协作。

8.3.9 量子强化学习的示例

量子 Q 学习（Quantum Q-Learning）：

状态表示： 使用量子比特来表示状态。
Q 值函数： 使用量子电路来近似 Q 值函数。
更新规则： 利用量子门操作来更新 Q 值函数。

量子策略梯度方法（Quantum Policy Gradient Methods）：

策略表示： 使用量子电路来表示策略函数。
梯度估计： 利用量子计算的优势来加速梯度估计过程。
策略优化： 通过优化量子电路的参数来优化策略函数。

四、量子强化学习的优势与挑战

8.3.10 优势

量子并行性： 量子计算可以利用叠加态同时处理多个状态或动作，从而加速学习过程。
量子纠缠： 量子纠缠可以创建智能体之间或状态之间的复杂关联，提高学习效率。
量子隧穿效应： 量子隧穿效应可以帮助优化算法跳出局部最优解，找到更优的策略。

8.3.11 挑战

量子资源需求： 实现量子强化学习需要大量的量子比特和量子门操作。
噪声和退相干： 量子强化学习容易受到噪声和退相干的影响，导致计算结果的误差。
算法设计： 设计有效的量子强化学习算法需要深入理解量子力学和强化学习理论。
硬件限制： 目前的量子硬件技术还无法实现大规模的量子强化学习，需要克服硬件限制。

五、量子强化学习的潜在应用

机器人控制： 利用量子计算的优势来实现更高效的机器人控制算法。
自动驾驶： 量子强化学习可以用于优化自动驾驶汽车的决策过程。
金融交易： 量子强化学习可以用于开发更智能的金融交易策略。
游戏 AI： 量子强化学习可以用于开发更强大的游戏 AI，例如，棋类游戏、策略游戏等。

六、总结

在本节中，我们深入探讨了量子强化学习：

背景与动机： 量子强化学习结合了量子计算和强化学习的优势，旨在优化决策过程。
基本概念： 量子强化学习利用量子态表示、量子计算加速和量子纠缠等方法来实现强化学习。
方法： 详细介绍了量子态表示、量子计算加速和量子纠缠与协作等方法。
优势与挑战： 量子强化学习具有量子并行性、量子纠缠和量子隧穿效应等优势，但也面临着量子资源需求、噪声和退相干等挑战。
应用： 量子强化学习在机器人控制、自动驾驶、金融交易和游戏 AI 等领域具有潜在应用。

量子强化学习是量子计算与人工智能交叉领域的前沿研究方向，它为解决复杂决策问题提供了新的思路和方法。通过学习和掌握量子强化学习，您可以更好地理解量子计算在人工智能中的应用，并为未来的量子计算研究提供重要的参考。

总而言之，量子强化学习是量子计算的重要组成部分，它融合了量子计算和强化学习的优势，为我们提供了一种全新的决策智能范式。希望这段旅程能够激发您对量子机器学习的兴趣，并为您的量子计算学习之旅提供一些启示。

第9章量子化学模拟

变分量子本征求解器（VQE）：分子基态的能量狩猎
量子相位估计算法：电子结构的精确测绘
费曼猜想验证：量子计算机的自然属性优势

9.1 变分量子本征求解器（VQE）：分子基态的能量狩猎

欢迎来到量子化学模拟的章节。在本章中，我们将深入探讨量子计算在化学领域的应用，特别是如何利用量子计算机来模拟分子结构和计算分子能量。这一领域的研究不仅对化学、材料科学和药物设计具有重要意义，还展示了量子计算解决实际问题的潜力。在本节中，我们将聚焦于变分量子本征求解器（Variational Quantum Eigensolver，VQE），一种利用量子计算来寻找分子基态能量的算法。让我们一同深入了解VQE的原理、实现方法及其在化学模拟中的革命性应用。

一、背景与动机：量子化学计算的挑战

在深入探讨VQE之前，我们需要了解量子化学计算面临的挑战，以及量子计算如何应对这些挑战。

9.1.1 量子化学计算的重要性

量子化学计算旨在通过求解薛定谔方程来预测分子的结构和性质，例如：

分子能量： 分子在不同状态下的能量。
电子结构： 电子在分子中的分布和运动。
化学反应： 化学反应的路径和能量变化。

9.1.2 经典计算方法的局限性

在经典计算中，量子化学计算主要依赖于以下方法：

哈特里-福克方法（Hartree-Fock Method）： 一种近似方法，但无法准确描述电子关联效应。
密度泛函理论（Density Functional Theory, DFT）： 考虑了电子关联效应，但精度有限。
耦合簇方法（Coupled Cluster Method）： 精度较高，但计算成本随分子大小呈指数级增长。

对于大型分子或复杂化学反应，经典方法的计算成本过高，甚至无法实现。

9.1.3 量子计算的优势

量子计算具有以下潜在优势，可以克服经典计算方法的局限性：

指数级并行性： 量子计算可以利用叠加态同时处理多个电子态。
量子纠缠： 量子纠缠可以准确描述电子之间的关联效应。
量子隧穿效应： 量子隧穿效应可以帮助优化算法更有效地找到分子基态。

二、VQE 算法概述

9.1.4 什么是 VQE？

变分量子本征求解器（VQE）是一种混合量子-经典算法，用于估计分子基态能量。其基本思想是：

变分原理： 任何试探波函数（trial wavefunction）的能量期望值都大于或等于真实基态能量。
参数化量子电路： 使用参数化量子电路来构建试探波函数。
经典优化： 利用经典优化算法来最小化能量期望值，从而逼近基态能量。

9.1.5 VQE 的优势

资源效率： 相对于其他量子算法（例如，量子相位估计算法），VQE 对量子资源的要求较低，更容易在当前的量子硬件上实现。
鲁棒性： VQE 对量子噪声和退相干具有一定的鲁棒性，因为它利用经典优化来纠正部分错误。
灵活性： VQE 可以与不同的量子电路结构和优化算法结合使用，具有很高的灵活性。

三、VQE 算法的步骤

9.1.6 量子态准备

1. 初始化： 准备 n 个量子比特，将其初始化到 ∣0⟩ 状态。

2. 参数化量子电路： 对量子比特应用参数化量子电路，将经典参数 θ 编码到量子态中：

其中，U(θ) 是参数化量子电路。

9.1.7 能量期望值计算

1. 哈密顿量映射： 将分子哈密顿量 HH 映射到量子算符上。

2. 测量： 对量子态 ∣ψ(θ)⟩ 进行测量，计算能量期望值：

由于直接测量 HH 是不可能的，需要将 HH 分解为一系列泡利算符的和：

其中，cici 是系数，PiPi 是泡利算符。

因此，能量期望值可以表示为：

通过对每个泡利算符进行测量，可以得到能量期望值。

9.1.8 经典优化

1.优化算法：使用经典优化算法（例如，梯度下降法、BFGS 算法等）来最小化能量期望值E(θ)。

2.参数更新：根据优化算法的输出，更新参数 θ 。

3.迭代：重复上述步骤，直到能量期望值收敛或达到预定的迭代次数。

9.1.9 结果输出

基态能量估计： 最终的能量期望值 E(θ) 是分子基态能量的估计值。
试探波函数： 优化后的量子态是分子基态的近似试探波函数。

四、VQE 算法的实现

9.1.10 量子电路结构

VQE 的性能在很大程度上取决于参数化量子电路的结构。常见的电路结构包括：

硬件高效电路： 电路结构与量子硬件的特性相匹配，例如，使用 CNOT 门和单量子比特旋转门。
UCC（Unitary Coupled Cluster）电路： 基于耦合簇理论的电路结构，可以更准确地描述电子关联效应。
自适应电路： 根据分子的特性，自适应地选择电路结构。

9.1.11 优化算法

选择合适的优化算法对于 VQE 的成功至关重要：

梯度下降法： 简单易实现，但可能陷入局部最优。
BFGS 算法： 拟牛顿法，收敛速度较快。
共轭梯度法： 适用于大规模优化问题。
进化算法： 例如，遗传算法，可以有效避免局部最优。

9.1.12 量子硬件实现

VQE 可以利用现有的量子硬件实现，例如：

超导电路： 例如，IBM 的量子处理器。
离子阱： 例如，Honeywell 的量子计算机。
光子量子计算： 例如，光学量子计算机。

五、VQE 算法的应用

分子能量计算： 计算分子的基态能量和激发态能量。
化学反应模拟： 模拟化学反应路径和能量变化。
材料科学： 预测材料的性质和结构。
药物设计： 预测药物分子与靶标的相互作用。

六、VQE 算法的优势与挑战

9.1.13 优势

资源效率： 相对于其他量子算法，VQE 对量子资源的要求较低。
鲁棒性： 对量子噪声和退相干具有一定的鲁棒性。
灵活性： 可以与不同的量子电路结构和优化算法结合使用。

9.1.14 挑战

优化问题： 寻找全局最优解是一个挑战，尤其是对于大型分子。
量子资源需求： 虽然 VQE 对量子资源的要求较低，但仍然需要大量的量子比特和量子门操作。
误差控制： 量子硬件的误差会影响 VQE 的结果，需要有效的误差控制机制。

七、总结

在本节中，我们深入探讨了变分量子本征求解器（VQE）：

背景与动机： 量子化学计算面临经典计算方法的局限性，量子计算提供了新的解决方案。
算法思想： 利用变分原理和参数化量子电路，通过经典优化来逼近分子基态能量。
算法步骤： 详细介绍了 VQE 的实现步骤，包括量子态准备、能量期望值计算、经典优化和结果输出。
实现方法： 讨论了量子电路结构、优化算法和量子硬件实现。
应用： VQE 在分子能量计算、化学反应模拟、材料科学和药物设计等领域具有应用前景。
优势与挑战： VQE 具有资源效率、鲁棒性和灵活性等优势，但也面临着优化问题、量子资源需求和误差控制等挑战。

VQE 是量子计算在化学模拟领域的重要应用，它展示了量子计算解决实际问题的潜力。通过学习和掌握 VQE，您可以更好地理解量子计算在化学中的应用，并为未来的量子计算研究提供重要的参考。

总而言之，VQE 是量子化学模拟的重要组成部分，它利用量子计算的优势，为我们提供了一种全新的分子能量计算方法。希望这段旅程能够激发您对量子化学模拟的兴趣，并为您的量子计算学习之旅提供一些启示。

9.2 量子相位估计算法：电子结构的精确测绘

欢迎继续深入量子化学模拟的世界。在上一节中，我们探讨了变分量子本征求解器（VQE），它通过结合量子计算和经典优化，为分子基态能量的计算提供了一种高效且资源友好的方法。然而，VQE 是一种近似方法，其精度受到参数化量子电路和优化算法的限制。在本节中，我们将深入探讨另一种强大的量子算法——量子相位估计算法（Quantum Phase Estimation, QPE），它能够以极高的精度计算分子的电子结构，包括基态能量和其他性质。让我们一同揭开量子相位估计算法的神秘面纱，探索其在化学模拟中的革命性应用。

一、背景与动机：精确电子结构计算的需求

在深入探讨量子相位估计算法之前，我们需要了解精确电子结构计算的重要性以及经典计算方法的局限性。

9.2.1 电子结构计算的重要性

电子结构计算是量子化学的核心，它旨在确定分子的电子分布和能量状态，包括：

基态能量： 分子在基态下的能量。
激发态能量： 分子在不同激发态下的能量。
电子密度分布： 电子在分子中的空间分布。
化学键性质： 化学键的强度、长度和极性。

9.2.2 经典计算方法的局限性

经典计算方法在精确计算电子结构方面面临以下挑战：

哈特里-福克方法： 无法准确描述电子关联效应，导致结果不够精确。
密度泛函理论（DFT）： 虽然考虑了电子关联效应，但精度依赖于所选择的泛函，对于某些体系可能不够准确。
耦合簇方法（CC）： 精度较高，但计算成本随分子大小呈指数级增长，难以处理大型分子。

9.2.3 量子计算的优势

量子计算具有以下潜力，可以克服经典计算方法的局限性：

指数级并行性： 量子计算可以利用叠加态同时处理多个电子态。
量子纠缠： 量子纠缠可以准确描述电子之间的复杂关联。
量子相位估计算法： 能够以极高的精度计算分子的能量本征值。

二、量子相位估计算法概述

9.2.4 什么是量子相位估计算法？

量子相位估计算法（QPE）是一种量子算法，用于估计酉算符的本征值相位。在化学模拟中，QPE 可以用来计算分子哈密顿量的本征值，即分子的能量本征值。

9.2.5 QPE 的基本原理

QPE 的核心思想是利用量子傅里叶变换来估计酉算符的本征值相位。其主要步骤包括：

1.量子态准备：准备一个包含 n 个辅助量子比特的量子态，以及一个包含 m 个量子比特的量子态∣ψ⟩，其中∣ψ⟩ 是待估计相位的量子态。

2.应用哈达玛门：对辅助量子比特应用哈达玛门，将其制备成等概率叠加态。

3.应用受控酉变换：对每个辅助量子比特应用受控酉变换，其中 U 是待估计相位的酉算符。

4.应用量子傅里叶变换：对辅助量子比特应用量子傅里叶变换。

5.测量：对辅助量子比特进行测量，得到测量结果 k 。

6.相位估计：通过对 kk 进行经典计算，可以估计相位 ϕ 。

9.2.6 QPE 在化学模拟中的应用

在化学模拟中，QPE 可以用来计算分子哈密顿量 HH 的本征值：

1.定义酉算符：定义一个酉算符，其中 tt 是一个合适的参数。

2.应用 QPE：对量子态 ∣ψ⟩ 和辅助量子比特应用 QPE，得到 H 的本征值 E。

三、QPE 算法的步骤

9.2.7 量子态准备

1.初始化：准备 n+m 个量子比特，其中 nn 个用于辅助，mm 个用于存储分子波函数。

2.编码分子波函数：将分子波函数 ∣ψ⟩∣ψ⟩ 编码到 mm 个量子比特中。

3. 哈达玛门应用： 对辅助量子比特应用哈达玛门：

9.2.8 受控酉变换

1. 定义受控酉变换： 对每个辅助量子比特应用受控酉变换 U2kU2k，其中 U=eiHtU=eiHt。

2. 状态演化： 状态变为：

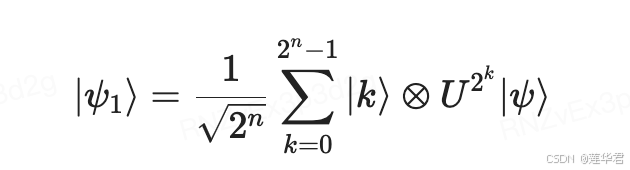
由于，因此：

状态可以表示为：

9.2.9 量子傅里叶变换

1. 应用量子傅里叶变换： 对辅助量子比特应用量子傅里叶变换：

9.2.10 测量与相位估计

1.测量辅助量子比特：测量辅助量子比特，得到测量结果 j 。

2.相位估计：通过对 jj 进行经典计算，可以估计相位。

四、QPE 算法的优势与挑战

9.2.11 优势

高精度： QPE 能够以极高的精度计算分子的能量本征值。
理论保证： QPE 提供了理论上的保证，即误差可以随辅助量子比特数量增加而指数级降低。

9.2.12 挑战

量子资源需求： QPE 需要大量的辅助量子比特和量子门操作。
深度量子电路： QPE 的量子电路深度较大，容易受到退相干的影响。
硬件实现： 目前的量子硬件技术还无法实现大规模的 QPE，需要克服硬件限制。

五、QPE 与 VQE 的比较

特性	VQE	QPE
精度	近似方法，精度依赖于参数化量子电路和优化算法	高精度，误差随辅助量子比特数量增加而指数级降低
量子资源需求	较低	较高
电路深度	较浅	较深
对退相干的敏感性	较低	较高
硬件实现难度	较低	较高

六、总结

在本节中，我们深入探讨了量子相位估计算法：

背景与动机： 精确的电子结构计算对化学模拟至关重要，经典计算方法存在局限性。
算法思想： 利用量子傅里叶变换来估计分子哈密顿量的本征值相位。
算法步骤： 详细介绍了 QPE 的实现步骤，包括量子态准备、受控酉变换、量子傅里叶变换、测量与相位估计。
优势与挑战： QPE 具有高精度和理论保证，但也面临着量子资源需求、电路深度和硬件实现等挑战。
与 VQE 的比较： QPE 和 VQE 各有优缺点，VQE 更适合当前量子硬件的限制，而 QPE 提供了更高的精度。

QPE 是量子化学模拟中的一种强大工具，它能够以极高的精度计算分子的电子结构，为化学研究提供了新的可能性。通过学习和掌握 QPE，您可以更好地理解量子计算在化学中的应用，并为未来的量子计算研究提供重要的参考。

总而言之，QPE 是量子化学模拟的重要组成部分，它利用量子计算的优势，为我们提供了一种精确的电子结构计算方法。希望这段旅程能够激发您对量子化学模拟的兴趣，并为您的量子计算学习之旅提供一些启示。

9.3 费曼猜想验证：量子计算机的自然属性优势

欢迎来到量子化学模拟章节的最后一节。在前两节中，我们探讨了变分量子本征求解器（VQE）和量子相位估计算法（QPE），它们展示了量子计算在计算分子能量和电子结构方面的强大潜力。然而，量子计算在化学模拟中的应用远不止于此。在本节中，我们将深入探讨费曼猜想（Feynman Conjecture），以及量子计算机如何利用其自然属性来模拟量子系统。这一猜想不仅为量子计算的应用提供了理论依据，还揭示了量子计算机在模拟复杂量子系统方面的独特优势。让我们一同深入了解费曼猜想的内容、验证过程及其对量子化学模拟的深远影响。

一、费曼猜想的提出

9.3.1 费曼猜想的背景

1981年，著名物理学家理查德·费曼（Richard Feynman）在一次演讲中提出了一个开创性的问题：

问题： 经典计算机能否有效地模拟量子系统？

9.3.2 经典计算机的局限性

费曼指出，经典计算机在模拟量子系统方面存在以下局限性：

1.指数级资源需求：经典计算机需要指数级的资源（例如，内存和计算时间）来模拟量子系统的演化。

例如，一个包含 n 个量子比特的量子系统，其状态空间维度为 2^n。要精确模拟其演化，经典计算机需要存储和处理 2^n 个复数。

2.复杂量子关联：量子系统中的纠缠和叠加效应难以用经典计算机准确描述。

9.3.3 费曼的猜想

基于上述局限性，费曼提出了以下猜想：

猜想： 量子系统只能被量子计算机有效地模拟。

换句话说，只有量子计算机才能有效地模拟量子系统的行为。

二、费曼猜想的内容

费曼猜想可以概括如下：

1.量子系统的模拟：模拟量子系统的演化需要精确地描述其量子态和量子关联。

2.经典计算的局限性：经典计算机由于其固有的局限性，无法有效地模拟大型量子系统。

3.量子计算的优势：量子计算机可以利用其自身的量子特性（例如，叠加性、纠缠性和幺正性）来模拟量子系统，而无需指数级的资源。

三、费曼猜想的验证

9.3.4 量子模拟的概念

量子模拟（Quantum Simulation）是指利用量子计算机来模拟量子系统的行为。其主要目标包括：

研究量子多体问题： 例如，凝聚态物理中的强关联电子系统。
模拟化学反应： 模拟化学反应路径和能量变化。
研究量子相变： 研究量子系统在相变过程中的行为。

9.3.5 量子模拟的实现方法

量子模拟可以通过以下几种方法实现：

1. 数字量子模拟（Digital Quantum Simulation）： 利用量子门操作来模拟量子系统的演化。

优点： 通用性强，可以模拟各种量子系统。
缺点： 需要大量的量子门操作，容易受到退相干的影响。

2. 模拟量子模拟（Analog Quantum Simulation）： 利用可控的量子系统（例如，超导电路、离子阱）来模拟目标量子系统。

优点： 硬件实现相对简单，可以模拟特定的量子系统。
缺点： 通用性较差，只能模拟特定的量子系统。

3.混合量子-经典模拟（Hybrid Quantum-Classical Simulation）：结合量子计算和经典计算的优势，例如，利用量子计算机计算关键部分，利用经典计算机处理其他部分。

9.3.6 费曼猜想的实验验证

近年来，科学家们在量子模拟方面取得了重要进展，验证了费曼猜想的正确性：

超导量子模拟器： 例如，谷歌的“悬铃木”处理器被用于模拟量子多体系统，展示了量子模拟的优势。
离子阱量子模拟： 例如，科学家们利用离子阱量子计算机模拟了量子磁性模型。
光子量子模拟： 例如，光子量子计算机被用于模拟量子化学系统。

这些实验结果表明，量子计算机能够有效地模拟量子系统的行为，验证了费曼猜想的正确性。

四、费曼猜想的意义

理论依据： 费曼猜想为量子计算的应用提供了重要的理论依据，证明了量子计算机在模拟量子系统方面的独特优势。
量子计算发展的推动力： 费曼猜想激励着科学家们探索量子模拟的应用，推动了量子计算技术的发展。
量子化学模拟的突破： 费曼猜想为量子化学模拟开辟了新的道路，使得精确模拟复杂化学反应和材料性质成为可能。

五、量子模拟的应用

化学和材料科学： 模拟分子结构和化学反应，设计新材料。
凝聚态物理： 研究强关联电子系统，探索新的物理现象。
量子多体物理： 研究量子多体系统的性质，例如，超导性、磁性等。
量子生物学： 模拟生物分子（例如，蛋白质、DNA）的结构和功能。

六、总结

在本节中，我们深入探讨了费曼猜想：

背景与动机： 费曼猜想源于经典计算机在模拟量子系统方面的局限性。
猜想内容： 只有量子计算机才能有效地模拟量子系统的行为。
验证过程： 通过量子模拟实验，验证了费曼猜想的正确性。
意义： 费曼猜想为量子计算的应用提供了理论依据，推动了量子计算和量子模拟的发展。
应用： 量子模拟在化学、材料科学、凝聚态物理、量子多体物理和量子生物学等领域具有广泛的应用前景。

费曼猜想是量子计算发展史上的一个重要里程碑，它揭示了量子计算机在模拟量子系统方面的独特优势，为量子计算的应用开辟了新的道路。希望这段旅程能够激发您对量子模拟的兴趣，并为您的量子计算学习之旅提供一些启示。

第四部分：量子工程实战篇

第10章量子硬件架构

超导量子芯片：约瑟夫森结的量子舞蹈
光子量子计算：量子隐形传态的工程实现
低温控制系统：稀释制冷机的绝对零度挑战

10.1 超导量子芯片：约瑟夫森结的量子舞蹈

欢迎来到量子硬件架构的章节。在本章中，我们将深入探讨实现量子计算的关键硬件技术之一——超导量子芯片。超导量子计算利用超导电路中的约瑟夫森结（Josephson Junction）来实现量子比特，并利用超导体的独特性质来操控和测量量子态。在本节中，我们将深入了解超导量子芯片的工作原理、关键技术挑战以及其在量子计算领域的应用前景。让我们一同踏上这段探索之旅，了解超导量子计算的“量子舞蹈”。

一、超导量子计算的兴起

10.1.1 超导量子计算的背景

超导量子计算是量子计算领域的一个重要分支，其发展可以追溯到20世纪90年代。随着对量子计算研究的深入，科学家们开始探索利用超导电路来实现量子比特的可能性。

10.1.2 超导体的独特性质

超导体具有以下独特性质，使其成为实现量子比特的理想候选者：

零电阻： 在临界温度以下，超导体电阻为零，电流可以无损耗地流动。
迈斯纳效应： 超导体排斥外部磁场，使其内部磁场为零。
宏观量子态： 超导体可以形成宏观尺度的量子态，例如，超导量子干涉仪（SQUID）。

二、超导量子比特的基本原理

10.1.3 约瑟夫森结

约瑟夫森结是超导量子比特的核心组件，它由两个超导体之间夹着一层薄薄的绝缘体构成。

约瑟夫森结的工作原理：

约瑟夫森效应： 当两个超导体之间存在弱耦合时，电子对（库珀对）可以通过隧道效应穿过绝缘体，形成超导电流。
相位差： 约瑟夫森结两端的超导体之间存在相位差，该相位差与通过结的电流和结两端的电压有关。

10.1.4 超导量子比特的类型

根据约瑟夫森结的不同配置和操控方式，超导量子比特可以分为以下几种主要类型：

1. 电荷量子比特（Charge Qubit）：

工作原理： 基于单个库珀对在两个超导岛之间的隧穿效应。
优点： 操作速度快，对电荷噪声敏感。
缺点： 对电荷噪声敏感，相干时间较短。

2. 磁通量子比特（Flux Qubit）：

工作原理： 基于超导环中磁通量的量子化状态。
优点： 对磁通噪声敏感，相干时间较长。
缺点： 对磁场噪声敏感，操控相对复杂。

3. 相位量子比特（Phase Qubit）：

工作原理： 基于约瑟夫森结中相位差的量子化状态。
优点： 相干时间较长，对相位噪声敏感。
缺点： 对相位噪声敏感，操控相对复杂。

4. 传输量子比特（Transmon Qubit）：

工作原理： 是一种改进的电荷量子比特，通过增加约瑟夫森结的电容来降低对电荷噪声的敏感性。
优点： 相干时间较长，对电荷噪声不敏感，易于操控。
缺点： 占用空间较大。

10.1.5 超导量子比特的操控与测量

操控： 通过微波脉冲（例如，射频脉冲）来操控超导量子比特的量子态。微波脉冲的频率、幅度和持续时间决定了量子态的演化。
测量： 通常采用量子态读取（Quantum State Readout）技术，例如，色散读取（Dispersive Readout）。该技术利用超导量子比特与谐振腔的相互作用，通过测量谐振腔的频率变化来推断量子比特的状态。

三、超导量子芯片的架构

10.1.6 单量子比特架构

一个基本的超导量子比特芯片包含以下组件：

约瑟夫森结： 实现量子比特的非线性元件。
电容： 与约瑟夫森结并联，用于调节量子比特的频率。
微波线路： 用于施加微波脉冲来操控量子比特。
谐振腔： 用于量子态读取。

10.1.7 多量子比特架构

为了实现多量子比特系统，需要将多个单量子比特单元集成在一起，并实现量子比特之间的耦合。

耦合方式： 常见的耦合方式包括电容耦合、电感耦合和谐振腔耦合。
布线挑战： 随着量子比特数量的增加，布线复杂度呈指数级增长，需要开发新的布线技术，例如，三维布线。

10.1.8 量子纠错架构

为了实现容错量子计算，超导量子芯片需要集成量子纠错功能：

表面编码： 利用二维量子比特阵列中的稳定子来实现量子纠错。
量子纠错码实现： 例如，重复码、稳定子码等。
错误检测与纠正： 通过量子态测量和量子门操作来实现错误检测与纠正。

四、超导量子计算的优势与挑战

10.1.9 优势

可扩展性： 超导量子比特可以利用现有的半导体制造技术进行大规模集成。
操控精度高： 微波脉冲操控可以实现高精度的量子门操作。
与经典电子器件兼容： 可以利用现有的电子技术进行控制和测量。

10.1.10 挑战

相干时间有限： 超导量子比特的相干时间通常在微秒量级，需要强大的量子纠错技术。
对环境敏感： 需要极低温环境（通常在 10-20 mK）来抑制热噪声。
制造工艺复杂： 需要精确的制造工艺来控制约瑟夫森结的特性。
布线复杂度高： 随着量子比特数量的增加，布线复杂度呈指数级增长。

五、超导量子计算的应用前景

量子模拟： 超导量子计算机可以用于模拟复杂的量子系统，例如，分子结构、化学反应和材料性质。
量子算法实现： 例如，Shor 算法和 Grover 算法，可以用于密码学、搜索和优化等领域。
量子机器学习： 超导量子计算机可以用于构建量子神经网络和量子核方法，用于模式识别、数据分析和决策优化。

六、总结

在本节中，我们深入探讨了超导量子芯片：

基本原理： 超导量子比特的核心组件是约瑟夫森结，其工作原理基于约瑟夫森效应。
主要类型： 介绍了电荷量子比特、磁通量子比特、相位量子比特和传输量子比特等主要类型。
操控与测量： 讨论了微波脉冲操控和量子态读取技术。
架构： 描述了单量子比特和多量子比特架构，以及量子纠错架构。
优势与挑战： 超导量子计算具有可扩展性、操控精度高等优势，但也面临着相干时间有限、对环境敏感等挑战。
应用前景： 超导量子计算在量子模拟、量子算法实现和量子机器学习等领域具有广阔的应用前景。

超导量子芯片是实现超导量子计算的关键硬件，其发展对量子计算的未来至关重要。通过学习和掌握超导量子芯片的知识，您可以更好地理解超导量子计算的实现方式，并为未来的量子计算研究提供重要的参考。

总而言之，超导量子芯片是量子计算的重要组成部分，它利用约瑟夫森结的独特性质，为我们提供了一种实现量子计算的有效途径。希望这段旅程能够激发您对超导量子计算的兴趣，并为您的量子计算学习之旅提供一些启示。

10.2 光子量子计算：量子隐形传态的工程实现

欢迎继续深入量子硬件架构的世界。在上一节中，我们探讨了超导量子芯片，它利用约瑟夫森结和超导体的独特性质来实现量子计算。在本节中，我们将把目光转向另一种重要的量子计算实现方案——光子量子计算。光子量子计算利用光子的量子特性，例如，叠加性、纠缠性和相干性，来执行量子计算任务。光子量子计算的一个突出优势在于其与现有光纤通信技术的兼容性，这使得它成为实现量子网络和量子通信的有力候选者。让我们一同深入了解光子量子计算的原理、技术挑战及其应用前景。

一、光子量子计算的基本原理

10.2.1 光子的量子特性

光子是光的基本粒子，具有以下量子特性，使其成为量子计算的理想载体：

叠加性： 光子可以处于多个状态的叠加态，例如，水平和垂直偏振态的叠加。
纠缠性： 两个或多个光子可以形成纠缠态，例如，贝尔态。
相干性： 光子可以在长距离上保持其量子相干性。
无相互作用： 光子之间几乎没有相互作用，这使得它们在传输过程中不易受到干扰。

10.2.2 光子量子比特

在光子量子计算中，量子比特（qubit）通常由光子的不同自由度来表示，例如：

偏振： 例如，水平偏振 ∣H⟩ 和垂直偏振 ∣V⟩。
路径： 光子通过不同路径传播，例如，左路径 ∣L⟩ 和右路径 ∣R⟩ 。
时间： 光子在不同时间到达，例如，早到∣E⟩ 和晚到∣L⟩。

10.2.3 光子量子门

光子量子门是实现光子量子计算的基本操作单元。常见的单光子量子门包括：

偏振旋转门： 例如，波片（Wave Plate），用于旋转光子的偏振态。
分束器（Beam Splitter）： 将光子分成两个路径，实现叠加态。
相位门： 改变光子的相位。

双光子量子门，例如，控制非门（CNOT Gate），可以通过以下方式实现：

非线性光学过程： 利用非线性光学晶体（例如，β-硼酸钡晶体）实现光子之间的相互作用。
线性光学量子计算（LOQC）： 结合分束器、相位门和单光子探测器，利用测量诱导的非线性来实现 CNOT 门。

二、光子量子计算的实现方案

10.2.4 线性光学量子计算（LOQC）

LOQC 是光子量子计算的一种重要实现方案，其核心思想是利用线性光学元件（例如，分束器、相位门）和测量诱导的非线性来实现量子门操作。

主要特点：

可扩展性： LOQC 可以利用现有的光学技术和设备实现。
高保真度： 光子量子态在传输过程中不易受到干扰，量子门操作的保真度较高。
挑战： 实现 CNOT 门等非线性量子门需要复杂的线性光学网络和精确的测量控制。

10.2.5 集成光子量子计算

集成光子量子计算旨在将光子量子器件集成到芯片上，以实现更紧凑、更稳定和更高效的光子量子计算系统。

主要特点：

小型化： 将光学元件集成到芯片上，可以大大减小系统的体积。
稳定性： 集成光学器件可以提供更高的稳定性和可重复性。
可扩展性： 集成光子芯片可以更容易地实现大规模集成。

10.2.6 拓扑光子量子计算

拓扑光子量子计算利用拓扑光子态来实现量子计算，其优势在于对局部扰动的免疫力。

主要特点：

拓扑保护： 拓扑光子态对局部扰动不敏感，具有很强的抗噪声能力。
高保真度： 拓扑保护可以提高量子门操作的保真度。
挑战： 实现拓扑光子态和相应的量子门操作需要克服许多技术挑战。

三、光子量子计算的优势与挑战

10.2.7 优势

高速度： 光子以光速传播，量子门操作速度极快。
长距离传输： 光子可以在长距离上保持其量子相干性，适合用于量子通信。
与光纤通信兼容： 光子量子计算可以与现有的光纤通信技术无缝集成。
无相互作用： 光子之间几乎没有相互作用，减少了量子态之间的串扰。

10.2.8 挑战

非线性量子门： 实现非线性量子门（例如，CNOT 门）需要复杂的线性光学网络和精确的测量控制。
光子损失： 光子在传输和操作过程中容易发生损失，需要有效的光子源和探测器。
可扩展性： 尽管集成光子技术可以提高可扩展性，但实现大规模光子量子计算机仍然面临挑战。
资源消耗： 光子量子计算通常需要大量的光学元件和资源。

四、光子量子计算的应用

量子通信： 光子量子计算可以用于实现量子密钥分发、量子隐形传态和量子网络。
量子模拟： 光子量子计算机可以用于模拟量子系统，例如，量子化学和凝聚态物理。
量子算法实现： 例如，量子傅里叶变换和量子相位估计算法，可以用于密码学和优化问题。
量子机器学习： 光子量子计算可以用于构建量子神经网络和量子核方法，用于模式识别和数据处理。

五、量子隐形传态：光子量子计算的标志性应用

10.2.9 什么是量子隐形传态？

量子隐形传态（Quantum Teleportation）是一种利用量子纠缠和经典通信来实现量子态传输的技术。

10.2.10 量子隐形传态的原理

量子隐形传态的原理可以概括如下：

1.量子纠缠：制备一对纠缠态光子，例如，贝尔态。

2.量子态传输：将要传输的量子态与纠缠态中的一个光子进行贝尔测量。

3.经典通信：将测量结果通过经典信道发送给接收方。

4.量子态重建：接收方根据经典信息对纠缠态中的另一个光子进行相应的量子门操作，从而重建出原始量子态。

10.2.11 光子量子计算与量子隐形传态

光子量子计算为实现量子隐形传态提供了理想的平台：

光子纠缠： 光子纠缠态易于制备和操控。
长距离传输： 光子可以在长距离上保持其量子相干性。
线性光学实现： 线性光学元件可以用于实现量子隐形传态所需的量子门操作和测量。

六、总结

在本节中，我们深入探讨了光子量子计算：

基本原理： 光子量子计算利用光子的量子特性，例如，叠加性、纠缠性和相干性。
光子量子比特： 光子量子比特可以通过偏振、路径和时间等自由度来表示。
光子量子门： 介绍了偏振旋转门、分束器、相位门和 CNOT 门等常见的光子量子门。
实现方案： 讨论了线性光学量子计算、集成光子量子计算和拓扑光子量子计算等实现方案。
优势与挑战： 光子量子计算具有高速度、长距离传输和与光纤通信兼容等优势，但也面临着非线性量子门、光子损失和可扩展性等挑战。
应用： 光子量子计算在量子通信、量子模拟、量子算法实现和量子机器学习等领域具有应用前景。
量子隐形传态： 光子量子计算为实现量子隐形传态提供了理想的平台。

光子量子计算是量子计算领域的重要组成部分，它利用光子的独特性质，为我们提供了一种实现量子计算的有效途径。希望这段旅程能够激发您对光子量子计算的兴趣，并为您的量子计算学习之旅提供一些启示。

10.3 低温控制系统：稀释制冷机的绝对零度挑战

欢迎来到量子硬件架构章节的最后一节。在前两节中，我们探讨了超导量子芯片和光子量子计算，它们分别利用超导体和光子的独特性质来实现量子计算。然而，无论选择哪种物理载体，低温环境都是实现量子计算的关键因素之一。在本节中，我们将深入探讨低温控制系统，特别是稀释制冷机（Dilution Refrigerator），它是目前实现量子计算所需极低温环境的主要技术手段。让我们一同深入了解稀释制冷机的工作原理、技术挑战及其在量子计算中的关键作用。

一、低温环境的必要性

在深入探讨稀释制冷机之前，我们需要了解为什么量子计算需要如此极端的低温环境。

10.3.1 量子退相干与热噪声

量子退相干： 量子系统与环境相互作用，导致量子相干性丧失，是量子计算面临的主要挑战之一。
热噪声： 环境中的热能会导致量子系统发生非相干跃迁，从而破坏量子态。
温度与退相干： 温度越高，热噪声越强，量子退相干的速度越快。

10.3.2 低温环境的作用

抑制热噪声： 通过降低温度，可以有效抑制热噪声的影响，从而延长量子比特的相干时间。
提高量子态稳定性： 低温环境可以提高量子态的稳定性，减少量子态的随机波动。

10.3.3 量子计算对温度的要求

不同的量子计算实现方案对温度的要求不同：

超导量子计算： 需要极低温环境（通常在 10-20 mK），以实现超导态并抑制热噪声。
离子阱量子计算： 可以在相对较高的温度下工作（几开尔文），但仍然需要低温来提高相干时间。
拓扑量子计算： 对温度的要求取决于具体的实现方案，但通常也需要低温环境。

二、稀释制冷机的工作原理

10.3.4 什么是稀释制冷机？

稀释制冷机是一种利用氦的同位素（氦-3 和氦-4）来实现极低温的设备。它是目前能够达到最低温度的制冷技术之一，通常可以将温度降低到 10 mK 左右。

10.3.5 稀释制冷机的工作循环

稀释制冷机的工作循环可以分为以下几个阶段：

1.预冷阶段：利用液氦-4 和液氮将系统预冷到 4 K 左右。

2.氦-3/氦-4 混合制冷：

混合室： 在混合室中，氦-3 和氦-4 形成一个混合液体。
相分离： 在低温下，氦-3 和氦-4 会发生相分离，形成富氦-3 相和贫氦-3 相。
蒸发制冷： 富氦-3 相的蒸发会带走热量，从而进一步降低温度。

3.循环过程：通过不断循环氦-3 和氦-4 的混合和分离过程，实现持续的制冷效果。

10.3.6 稀释制冷机的关键组件

压缩机： 提供制冷所需的动力。
热交换器： 用于传递热量，提高制冷效率。
混合室： 氦-3 和氦-4 发生相分离的地方。
冷板： 连接到量子芯片，提供极低温环境。

三、稀释制冷机的技术挑战

10.3.7 温度稳定性

挑战： 维持稳定的极低温环境对于量子计算至关重要，任何温度波动都会影响量子比特的性能。
解决方案： 采用精密的温度控制系统，例如，PID 控制器，来维持温度的稳定性。

10.3.8 制冷效率

挑战： 稀释制冷机的制冷效率相对较低，需要消耗大量的氦-3 和氦-4。
解决方案： 开发更高效的制冷循环和热交换器，以及回收和循环利用氦-3 和氦-4。

10.3.9 振动与噪声

挑战： 制冷机运行过程中产生的振动和电磁噪声会影响量子比特的性能。
解决方案： 采用减震和屏蔽技术，例如，使用振动隔离器和电磁屏蔽材料，来减少对量子比特的影响。

10.3.10 可靠性与维护

挑战： 稀释制冷机是一个复杂的系统，需要定期维护和保养。
解决方案： 提高制冷机的可靠性和自动化程度，例如，采用故障检测和诊断系统。

四、稀释制冷机在量子计算中的应用

10.3.11 超导量子计算

稀释制冷机是超导量子计算的核心组件：

提供极低温环境： 将超导量子芯片冷却到 10-20 mK，以实现超导态并抑制热噪声。
量子比特操控与测量： 稀释制冷机内部集成了量子比特操控和测量所需的微波线路和电子设备。

10.3.12 其他量子计算方案

离子阱量子计算： 虽然可以在相对较高的温度下工作，但稀释制冷机可以进一步提高其相干时间。
拓扑量子计算： 某些拓扑量子计算方案也需要低温环境，稀释制冷机可以为其提供必要的温度条件。

五、总结

在本节中，我们深入探讨了低温控制系统，特别是稀释制冷机：

低温环境的必要性： 低温环境可以抑制热噪声，提高量子态的稳定性，是实现量子计算的关键。
稀释制冷机的工作原理： 利用氦-3 和氦-4 的相分离和蒸发制冷来实现极低温。
技术挑战： 温度稳定性、制冷效率、振动与噪声以及可靠性与维护是稀释制冷机面临的主要挑战。
应用： 稀释制冷机在超导量子计算和其他量子计算方案中发挥着至关重要的作用。

稀释制冷机是量子计算硬件架构的重要组成部分，它为量子计算的实现提供了必要的低温环境。通过学习和掌握稀释制冷机的知识，您可以更好地理解量子计算的实现方式，并为未来的量子计算研究提供重要的参考。

总而言之，稀释制冷机是量子计算的重要组成部分，它利用氦的同位素，为我们提供了一种实现极低温环境的有效途径。希望这段旅程能够激发您对量子硬件架构的兴趣，并为您的量子计算学习之旅提供一些启示。

第11章量子软件开发

量子编译优化：量子电路的综合与简化艺术
混合计算框架：CPU+QPU的协同作战策略
量子基准测试：量子体积（QV）的测量方法论

11.1 量子编译优化：量子电路的综合与简化艺术

欢迎来到量子软件开发的世界。在前面的章节中，我们探讨了量子计算的基本原理、量子算法、量子编程模型以及量子硬件架构。然而，要将量子计算的强大潜力转化为现实，还需要强大的软件开发工具和技术支持。在本章中，我们将深入探讨量子软件开发的关键领域，其中量子编译优化是至关重要的一环。在本节中，我们将深入了解量子编译优化的概念、目标、技术方法以及其在量子计算中的重要性。

一、量子编译优化的背景与动机

11.1.1 量子电路的复杂性

量子电路是量子计算的基本构建模块，但随着量子算法复杂性的增加，量子电路的规模和复杂性也在迅速增长：

量子门数量： 复杂的量子算法可能需要成千上万个量子门。
量子比特数量： 大规模量子计算需要大量的量子比特。
量子纠缠： 量子纠缠增加了量子电路的复杂性。

11.1.2 量子硬件的限制

当前的量子硬件技术还面临着诸多限制：

量子门保真度： 量子门操作的保真度有限，存在操作错误。
量子比特相干时间： 量子比特的相干时间有限，容易受到退相干的影响。
量子资源限制： 量子比特数量、量子门操作速度等资源有限。

11.1.3 量子编译优化的必要性

为了克服上述挑战，需要对量子电路进行优化：

减少量子门数量： 降低电路的复杂性和资源消耗。
缩短电路深度： 减少电路的深度，降低退相干的影响。
提高电路效率： 提高量子电路的执行效率，减少计算时间。

二、量子编译优化的目标

量子编译优化的主要目标包括：

1.电路简化：减少量子门的数量和类型，简化电路结构。

2.电路深度优化：减少电路的深度，降低退相干的影响。

3.资源优化：减少量子比特数量和量子门操作次数，提高资源利用率。

4.错误率降低：减少操作错误，提高量子电路的保真度。

5.可执行性：确保优化后的电路可以在目标量子硬件上执行。

三、量子编译优化的技术方法

11.1.4 门级优化

门合并： 将连续的相同门操作合并成单个门操作。例如，将连续的 Hadamard 门合并成一个 Hadamard 门。
门消除： 消除对电路输出没有影响的量子门操作。例如，消除对未使用的量子比特的操作。
门替换： 用等效的门操作替换复杂的门操作。例如，用 CNOT 门和单量子比特门替换复杂的双量子比特门。

11.1.5 电路级优化

量子电路重写： 重新排列量子门的顺序，以简化电路结构。例如，利用交换门的可交换性来重新排列量子门。
量子电路分解： 将复杂的量子门分解成更简单的门。例如，将一个多量子比特门分解成一系列 CNOT 门和单量子比特门。
量子电路模板匹配： 使用预定义的电路模板来识别和替换常见的电路模式。

11.1.6 基于图的优化

量子电路图表示： 将量子电路表示为图结构，例如，量子电路图（Quantum Circuit Graph）。
图算法应用： 利用图算法（例如，图的同构、图的匹配）来识别和优化电路结构。

11.1.7 基于机器学习的优化

机器学习模型： 使用机器学习模型（例如，深度神经网络）来学习量子电路优化的策略。
强化学习： 利用强化学习算法来探索和优化量子电路的结构和参数。

11.1.8 混合优化方法

结合多种方法： 将不同的优化方法结合起来，例如，门级优化和电路级优化相结合，以实现更有效的优化。
迭代优化： 采用迭代优化的方法，逐步改进量子电路的性能。

四、量子编译优化的挑战

优化空间巨大： 量子电路的优化空间是指数级的，寻找全局最优解是一个巨大的挑战。
优化算法复杂度： 许多优化算法本身具有较高的计算复杂度，难以应用于大规模量子电路。
硬件限制： 优化后的电路必须考虑量子硬件的限制，例如，量子门集、量子比特连接性等。
错误率权衡： 优化过程需要在减少电路复杂性和降低错误率之间进行权衡。

五、量子编译优化的工具与框架

Qiskit Transpiler（IBM）： Qiskit 提供的量子电路优化工具，支持多种优化方法和后端目标。
Cirq（Google）： Cirq 提供了丰富的量子电路优化工具，例如，门合并、电路重写等。
t|ket⟩（Cambridge Quantum Computing）： 一个功能强大的量子电路优化和编译工具，支持多种量子硬件平台。
Forest（Rigetti Computing）： Rigetti 提供的量子软件开发框架，包含量子电路优化工具。

六、量子编译优化的应用

量子算法实现： 优化量子电路以实现更高效的量子算法，例如，Shor 算法和 Grover 算法。
量子模拟： 优化量子电路以模拟复杂的量子系统，例如，分子结构和化学反应。
量子机器学习： 优化量子电路以构建更高效的量子机器学习模型，例如，量子神经网络和量子核方法。
量子纠错： 优化量子电路以实现更有效的量子纠错码，例如，表面编码和稳定子码。

七、总结

在本节中，我们深入探讨了量子编译优化：

背景与动机： 量子电路的复杂性和量子硬件的限制使得量子编译优化成为必要。
优化目标： 电路简化、深度优化、资源优化、错误率降低和可执行性是量子编译优化的主要目标。
技术方法： 门级优化、电路级优化、基于图的优化、基于机器学习的优化以及混合优化方法是量子编译优化的主要方法。
挑战： 优化空间巨大、算法复杂度高、硬件限制和错误率权衡是量子编译优化面临的主要挑战。
工具与框架： Qiskit、Cirq、t|ket⟩ 和 Forest 等是常用的量子编译优化工具和框架。
应用： 量子编译优化在量子算法实现、量子模拟、量子机器学习和量子纠错等领域具有广泛的应用。

量子编译优化是量子软件开发的重要组成部分，它为实现高效的量子计算提供了关键的技术支持。通过学习和掌握量子编译优化的知识，您可以更好地理解量子电路优化的核心技术，并为未来的量子计算研究提供重要的参考。

总而言之，量子编译优化是量子计算的重要组成部分，它利用各种优化技术，为我们提供了一种实现高效量子电路的有效途径。希望这段旅程能够激发您对量子软件开发的兴趣，并为您的量子计算学习之旅提供一些启示。

11.2 混合计算框架：CPU+QPU的协同作战策略 —— 构建经典与量子计算的桥梁

欢迎继续深入量子软件开发的旅程。在上一节中，我们探讨了量子编译优化，它通过优化量子电路的结构和参数来提高量子计算的效率。在本节中，我们将探讨另一个至关重要的主题——混合计算框架，特别是 CPU（经典处理器）+ QPU（量子处理单元）的协同工作模式。随着量子计算技术的不断发展，经典计算和量子计算的融合已成为一种必然趋势。混合计算框架旨在充分利用经典计算和量子计算的优势，为解决复杂问题提供更强大的工具。让我们一同深入了解混合计算框架的原理、架构、优势以及其在实际应用中的潜力。

一、混合计算框架的背景与动机

11.2.1 经典计算与量子计算的互补性

经典计算的优势： 经典计算机在处理逻辑运算、数据存储、输入输出以及控制任务方面具有成熟的技术和广泛的应用。
量子计算的优势： 量子计算机在解决某些特定问题（例如，整数分解、量子模拟、组合优化）上具有指数级的加速潜力。

11.2.2 量子计算的局限性

尽管量子计算前景广阔，但目前仍处于发展初期，面临着诸多挑战：

量子硬件限制： 量子比特的数量、相干时间和错误率都有限。
量子算法复杂性： 并非所有问题都适合用量子算法解决。
量子-经典接口： 需要有效的接口来实现经典计算与量子计算的交互。

11.2.3 混合计算框架的提出

为了克服上述挑战，混合计算框架应运而生，其核心思想是：

协同工作： 结合经典计算和量子计算的优势，让它们协同工作。
任务分解： 将复杂问题分解成适合经典计算和量子计算处理的部分。
资源优化： 充分利用现有的经典计算资源，同时探索量子计算的优势。

二、混合计算框架的架构

11.2.4 基本架构

混合计算框架通常包含以下组件：

1.经典处理器（CPU）：负责执行经典计算任务，例如，数据预处理、经典算法执行、量子电路控制等。

2.量子处理单元（QPU）：负责执行量子计算任务，例如，量子门操作、量子态制备、量子测量等。

3.经典-量子接口：实现经典处理器与量子处理单元之间的通信和数据传输。

4.量子编译：将高级量子算法转换为可执行的量子电路，并进行优化。

5.经典后处理：对量子计算的结果进行经典计算，例如，数据分析、误差校正等。

11.2.5 通信与数据传输

经典-量子通信： 经典处理器通过控制线路向量子处理单元发送指令和数据，例如，量子门操作序列、量子比特初始化参数等。
量子-经典通信： 量子处理单元将测量结果传输回经典处理器，例如，量子态的测量值、量子电路的输出等。

11.2.6 任务分配与协调

任务分解： 将问题分解成适合经典计算和量子计算处理的部分。例如，在量子化学模拟中，经典处理器可以处理分子结构的预处理，而量子处理单元可以执行量子态演化和能量计算。
协同调度： 协调经典处理器和量子处理单元的任务执行顺序，确保资源的高效利用和任务的正确执行。
错误处理与容错： 处理量子计算过程中出现的错误，例如，量子门操作错误、量子比特退相干等。

三、混合计算框架的优势

11.2.7 性能提升

量子加速： 利用量子计算的优势，解决经典计算难以解决的问题，例如，整数分解、量子模拟等。
经典辅助： 利用经典计算的优势，处理量子计算无法高效处理的任务，例如，数据预处理、经典算法执行等。

11.2.8 资源优化

资源复用： 经典处理器和量子处理单元可以共享资源，例如，内存、存储等。
效率提升： 通过合理分配任务，减少量子计算资源的消耗，提高整体计算效率。

11.2.9 灵活性与可扩展性

模块化设计： 混合计算框架通常采用模块化设计，可以根据需要添加或替换组件。
可扩展性： 可以随着量子硬件的发展，逐步扩展量子计算的能力。

四、混合计算框架的应用

11.2.10 量子化学模拟

经典处理器： 处理分子结构的预处理、经典力场计算等。
量子处理单元： 执行量子态演化和能量计算。

11.2.11 量子机器学习

经典处理器： 进行数据预处理、经典机器学习模型训练等。
量子处理单元： 执行量子态制备、量子门操作、量子测量等。

11.2.12 量子优化

经典处理器： 进行问题建模、经典优化算法执行等。
量子处理单元： 执行量子优化算法，例如，量子近似优化算法（OA）。

11.2.13 量子-经典混合算法

变分量子本征求解器（VQE）： 结合经典优化算法和量子电路，来寻找分子基态能量。
量子相位估计算法（QPE）： 利用经典处理器进行相位估计的后处理。

五、混合计算框架的挑战

经典-量子接口： 实现高效、可靠的经典-量子通信是一个挑战。
任务协调： 协调经典处理器和量子处理单元的任务执行顺序，避免资源冲突和瓶颈。
错误处理： 处理量子计算过程中的错误，并将其与经典计算的错误处理机制相结合。
软件工具： 开发支持混合计算的软件工具和框架，例如，编译器、调试器、优化器等。

六、混合计算框架的实现

IBM Quantum System One： IBM 提供的量子计算系统，结合了经典处理器和量子处理单元，并提供了混合编程接口。
Google Quantum Computing： Google 的量子计算平台，支持混合计算任务，例如，量子机器学习。
Rigetti Computing： Rigetti 提供的混合计算框架，结合了经典计算和量子计算的优势。
Microsoft Quantum Development Kit： 微软的量子开发工具包，支持混合量子-经典编程。

七、总结

在本节中，我们深入探讨了混合计算框架：

背景与动机： 经典计算和量子计算的互补性以及量子计算的局限性推动了混合计算框架的发展。
架构： 混合计算框架包含经典处理器、量子处理单元、经典-量子接口、量子编译和经典后处理等组件。
优势： 性能提升、资源优化、灵活性和可扩展性是混合计算框架的主要优势。
应用： 混合计算框架在量子化学模拟、量子机器学习、量子优化和量子-经典混合算法等领域具有广泛应用。
挑战： 经典-量子接口、任务协调、错误处理和软件工具是混合计算框架面临的主要挑战。
实现： IBM、Google、Rigetti 和微软等公司都在积极开发混合计算框架。

混合计算框架是量子软件开发的重要组成部分，它为实现经典与量子计算的协同工作提供了关键的技术支持。通过学习和掌握混合计算框架的知识，您可以更好地理解量子计算与经典计算的融合发展，并为未来的量子计算研究提供重要的参考。

总而言之，混合计算框架是连接经典与量子计算的桥梁，它利用两者的优势，为我们提供了一种解决复杂问题的新方法。希望这段旅程能够激发您对混合计算的兴趣，并为您的量子计算学习之旅提供一些启示。

11.3 量子基准测试：量子体积（QV）的测量方法论

欢迎来到量子软件开发章节的最后一节。在前两节中，我们探讨了量子编译优化和混合计算框架，它们分别关注于优化量子电路和提高经典与量子计算的协同效率。然而，要全面评估量子计算系统的性能，我们还需要一个标准化的方法来进行量子基准测试。在本节中，我们将深入探讨量子体积（Quantum Volume, QV），这是一种被广泛接受的用于评估量子计算系统整体能力的指标。量子体积不仅考虑了量子比特的数量，还综合了量子门的保真度、连通比特的连通性、量子电路的深度等因素。让我们一同深入了解量子体积的概念、测量方法及其在量子计算中的重要性。

一、量子基准测试的必要性

在深入探讨量子体积之前，我们需要了解为什么需要量子基准测试。

11.3.1 量子计算系统的复杂性

量子计算系统是一个复杂的系统，其性能受到多种因素的影响：

量子比特数量： 量子比特数量越多，可以处理的问题规模越大。
量子门保真度： 量子门操作的保真度越高，量子计算的准确性越高。
量子比特连通性： 量子比特之间的连接性越好，量子电路的灵活性越高。
量子电路深度： 量子电路的深度越大，可以执行更复杂的量子算法。
退相干和错误率： 量子比特的相干时间越长，错误率越低，量子计算的可靠性越高。

11.3.2 单一指标的局限性

量子比特数量： 仅关注量子比特数量无法全面反映量子计算系统的性能。
量子门保真度： 仅考虑量子门保真度忽略了其他重要因素，例如，量子比特连通性和电路深度。
其他指标： 单独使用其他指标（例如，退相干时间、错误率）也无法全面评估量子计算系统的整体能力。

11.3.3 量子体积的定义

量子体积（QV）是一种综合指标，用于评估量子计算系统的整体能力。它考虑了以下因素：

量子比特数量（n）： 量子比特数量越多，量子体积越大。
量子门保真度： 量子门操作的保真度越高，量子体积越大。
量子比特连通性： 量子比特之间的连接性越好，量子体积越大。
量子电路深度（d）： 量子电路的深度越大，量子体积越大。

量子体积的定义可以表示为：

二、量子体积的测量方法

11.3.4 随机量子电路生成

量子体积的测量基于随机量子电路：

1.电路结构：随机量子电路通常由一系列层组成，每层包含随机选择的单量子比特门和双量子比特门（例如，CNOT 门）。

2.电路深度：电路的深度 d 与量子比特数量 n 相关，通常 d=n。

11.3.5 量子电路执行

1.量子电路编译：将随机量子电路编译成目标量子硬件可以执行的指令集。

2.量子电路执行：在量子硬件上执行编译后的量子电路。

3.测量结果：对量子比特进行测量，得到测量结果。

11.3.6 保真度计算

1. 理想结果： 计算理想情况下随机量子电路的输出概率分布。

2. 实际结果： 计算实际测量结果的概率分布。

3. 保真度： 计算理想结果和实际结果之间的保真度：

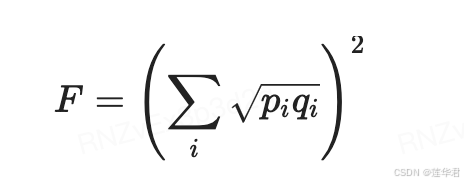
其中，pipi 是理想结果的概率，qiqi 是实际结果的概率。

11.3.7 量子体积确定

1.阈值判断：如果保真度达到预定的阈值（例如，2/3），则认为该随机量子电路执行成功。

2.最大量子体积：重复上述步骤，找到可以成功执行的最大 n ，从而确定量子体积 QV=2^n。

三、量子体积的优势与局限性

11.3.8 优势

综合性： 量子体积综合考虑了量子比特数量、量子门保真度、量子比特连通性和量子电路深度等因素。
标准化： 量子体积提供了一种标准化的方法来评估不同量子计算系统的性能。
可比较性： 不同量子计算系统的量子体积可以直接比较，便于评估其相对性能。

11.3.9 局限性

简化模型： 量子体积的测量基于随机量子电路，可能无法完全反映量子计算系统在特定应用中的性能。
资源消耗： 测量高量子体积需要大量的量子资源和计算时间。
硬件限制： 量子体积的测量依赖于量子硬件的当前技术水平，可能无法准确反映量子计算系统的潜在能力。

四、量子体积的应用

量子硬件评估： 量子体积可以用于评估不同量子硬件平台的性能，例如，超导量子计算机、离子阱量子计算机等。
量子算法优化： 量子体积可以帮助开发者了解量子硬件的限制，从而优化量子算法以适应硬件特性。
量子计算发展评估： 量子体积可以用于跟踪量子计算技术的发展趋势，评估不同技术路线的进展。

五、量子体积与其他量子基准测试指标

除了量子体积之外，还有其他一些量子基准测试指标，例如：

量子门保真度（Gate Fidelity）： 衡量量子门操作的准确性。
量子比特相干时间（Coherence Time）： 衡量量子比特保持量子相干性的时间。
错误率（Error Rate）： 衡量量子计算过程中发生错误的概率。
量子体积（QV）： 综合评估量子计算系统的整体能力。

量子体积与其他指标相比，具有以下特点：

综合性： 量子体积综合考虑了多个因素，而其他指标通常只关注单个方面。
实用性： 量子体积更贴近实际应用场景，而其他指标可能更侧重于理论评估。

六、总结

在本节中，我们深入探讨了量子体积：

必要性： 量子计算系统的复杂性需要一种综合的评估方法。
定义： 量子体积是一种综合指标，考虑了量子比特数量、量子门保真度、量子比特连通性和量子电路深度等因素。
测量方法： 基于随机量子电路，通过计算保真度来确定量子体积。
优势与局限性： 量子体积具有综合性、标准化和可比较性等优势，但也存在简化模型、资源消耗和硬件限制等局限性。
应用： 量子体积可以用于量子硬件评估、量子算法优化和量子计算发展评估。
与其他指标的比较： 量子体积与其他量子基准测试指标相比，具有综合性更强的特点。

量子体积是评估量子计算系统整体能力的重要指标，它为量子计算的发展提供了一个标准化的评估框架。通过学习和掌握量子体积的知识，您可以更好地理解量子计算系统的性能评估，并为未来的量子计算研究提供重要的参考。

总而言之，量子体积是量子计算的重要组成部分，它为我们提供了一种评估量子计算能力的新方法。希望这段旅程能够激发您对量子基准测试的兴趣，并为您的量子计算学习之旅提供一些启示。

第12章量子云平台

AWS Braket实战：混合量子经典工作流设计
量子即服务（QaaS）：商业模式的量子跃迁
安全通信协议：量子密钥分发的商业部署

12.1 AWS Braket实战：混合量子经典工作流设计

欢迎来到量子云平台的章节。在本章中，我们将深入探讨量子计算与云计算的融合，特别是如何利用云平台来访问和利用量子计算资源。在本节中，我们将聚焦于AWS Braket，这是亚马逊网络服务（AWS）提供的量子计算服务。通过AWS Braket，用户可以轻松地构建、测试和运行量子算法，并将其与经典计算资源无缝集成。在本节中，我们将通过一个实战案例来展示如何使用AWS Braket来设计混合量子经典工作流，并探讨其优势和实际应用。

一、AWS Braket概述

12.1.1 什么是AWS Braket？

AWS Braket是亚马逊推出的量子计算服务，旨在为研究人员和开发者提供一个访问量子计算资源的平台。其主要特点包括：

统一接口： 提供一个统一的API接口，简化了与不同量子硬件提供商的交互。
多种量子硬件支持： 支持多种量子硬件，包括超导量子计算机、离子阱量子计算机和量子模拟器。
混合量子-经典计算： 支持混合量子-经典工作流，允许用户将量子计算任务与经典计算资源集成。
可扩展性： 利用AWS的云基础设施，提供可扩展的计算资源。

12.1.2 AWS Braket的主要组件

1.量子计算服务：提供对量子硬件和模拟器的访问。

2.经典计算资源：提供对AWS经典计算资源的访问，例如，EC2实例、S3存储等。

3.开发工具：提供SDK（例如，Braket Python SDK）和开发工具包，方便用户编写和调试量子程序。

4.管理控制台：提供图形化界面，方便用户管理量子计算任务和资源。

二、混合量子经典工作流的设计

12.1.3 什么是混合量子经典工作流？

混合量子经典工作流是指将量子计算任务与经典计算任务结合起来，以解决复杂问题。这种方法结合了量子计算和经典计算的优势：

量子计算： 解决经典计算难以处理的问题，例如，量子模拟、整数分解等。
经典计算： 处理数据预处理、结果后处理、算法控制等任务。

12.1.4 工作流设计步骤

以下是一个使用AWS Braket设计混合量子经典工作流的示例步骤：

步骤1：问题定义与分解

目标： 解决一个复杂问题，例如，分子能量计算。
任务分解： 将问题分解成适合量子计算和经典计算处理的部分。
- 量子计算任务： 例如，计算分子基态能量。
- 经典计算任务： 例如，数据预处理、结果后处理、参数优化等。

步骤2：量子电路设计

选择量子算法： 例如，变分量子本征求解器（VQE）。
构建量子电路： 使用Braket Python SDK构建量子电路。
- 量子比特初始化： 将量子比特初始化到 ∣0⟩∣0⟩ 状态。
- 参数化量子门： 应用参数化量子门（例如，旋转门）来编码经典参数。
- 纠缠操作： 应用CNOT门或其他纠缠门来创建量子纠缠。
- 测量操作： 对量子比特进行测量，将量子态转换为经典输出。

示例代码：

python

取消自动换行

复制

from braket.circuits import Circuit
from braket.aws import AwsDevice

# 创建量子电路
qc = Circuit()
qc.h(0)
qc.cnot(0, 1)
qc.rx(angle, 0)
qc.ry(angle, 1)
qc.cnot(0, 1)
qc.measure_all()

# 选择量子设备
device = AwsDevice("arn:aws:braket:::device/quantum-simulator/amazon/sv1")

# 运行量子电路
task = device.run(qc, shots=1000)
result = task.result()
print(result.measurement_counts)

步骤3：经典计算任务

数据预处理： 对输入数据进行预处理，例如，参数初始化、特征提取等。
参数优化： 使用经典优化算法（例如，梯度下降法）来优化量子电路的参数。
结果后处理： 对量子计算的结果进行后处理，例如，计算能量期望值、分析结果等。

示例代码：

python

取消自动换行

复制

import numpy as np
from scipy.optimize import minimize

# 定义损失函数
def loss_function(params):
    # 设置量子电路参数
    qc = Circuit()
    qc.h(0)
    qc.cnot(0, 1)
    qc.rx(params[0], 0)
    qc.ry(params[1], 1)
    qc.cnot(0, 1)
    qc.measure_all()
    
    # 运行量子电路
    task = device.run(qc, shots=1000)
    result = task.result()
    counts = result.measurement_counts
    
    # 计算能量期望值
    energy = 0
    for bitstring, count in counts.items():
        # 假设能量计算公式
        energy += count * (int(bitstring[0]) + int(bitstring[1]))
    return energy / 1000

# 优化参数
initial_params = [0, 0]
result = minimize(loss_function, initial_params, method='BFGS')
optimal_params = result.x
print("Optimal parameters:", optimal_params)

步骤4：工作流执行与协调

任务调度： 使用AWS Braket的任务调度功能来协调量子计算任务和经典计算任务的执行顺序。
资源管理： 利用AWS的资源管理工具来分配和管理计算资源，例如，CPU、内存、存储等。

步骤5：结果分析与可视化

结果分析： 对混合工作流的结果进行分析，例如，比较不同参数设置下的能量值。
结果可视化： 使用可视化工具（例如，Matplotlib）来展示结果，例如，能量曲线、概率分布等。

示例代码：

python

取消自动换行

复制

import matplotlib.pyplot as plt

# 假设我们有一组能量值
energies = [loss_function([0, 0]), loss_function([0.1, 0.1]), loss_function([0.2, 0.2])]
plt.plot([0, 0.1, 0.2], energies, 'o-')
plt.xlabel('Parameter Value')
plt.ylabel('Energy')
plt.title('Energy vs. Parameter')
plt.show()

三、混合量子经典工作流的优势

性能提升： 结合量子计算的优势，解决经典计算难以处理的问题。
资源优化： 利用经典计算资源来处理数据预处理、结果后处理等任务，提高整体效率。
灵活性： 可以根据需要调整量子计算和经典计算的任务分配，以适应不同的应用场景。
可扩展性： 利用AWS的云基础设施，可以轻松地扩展计算资源，以满足不断增长的需求。

四、实际应用案例

案例1：分子能量计算

目标： 计算分子的基态能量。
量子计算任务： 使用VQE算法来估计分子哈密顿量的本征值。
经典计算任务： 进行数据预处理、参数优化、结果后处理等。

案例2：量子化学模拟

目标： 模拟化学反应路径和能量变化。
量子计算任务： 使用量子相位估计算法来计算能量本征值。
经典计算任务： 进行分子结构预处理、结果分析等。

案例3：量子机器学习

目标： 构建量子神经网络进行模式识别。
量子计算任务： 使用量子电路来实现神经网络的前向传播。
经典计算任务： 进行数据预处理、参数训练、结果分析等。

五、总结

在本节中，我们深入探讨了AWS Braket及其在设计混合量子经典工作流中的应用：

AWS Braket概述： 提供了对量子硬件和模拟器的访问，并支持混合量子-经典计算。
混合量子经典工作流的设计： 详细介绍了工作流的设计步骤，包括问题定义与分解、量子电路设计、经典计算任务、工作流执行与协调以及结果分析与可视化。
优势： 性能提升、资源优化、灵活性和可扩展性是混合量子经典工作流的主要优势。
实际应用案例： 展示了混合量子经典工作流在分子能量计算、量子化学模拟和量子机器学习等领域的应用。

AWS Braket为用户提供了强大的工具来构建和运行混合量子经典工作流，使得量子计算的应用更加便捷和高效。通过学习和掌握AWS Braket的使用，您可以更好地利用量子计算的优势，并为未来的量子计算应用做好准备。

总而言之，AWS Braket是量子云平台的重要组成部分，它为我们提供了一种访问和利用量子计算资源的有效途径。希望这段旅程能够激发您对量子云平台的兴趣，并为您的量子计算学习之旅提供一些启示。

12.2 量子即服务（QaaS）：商业模式的量子跃迁

欢迎继续深入量子云平台的世界。在上一节中，我们探讨了AWS Braket，它为用户提供了访问量子计算资源的平台，并支持混合量子-经典工作流的设计。在本节中，我们将探讨一种新兴的商业模式——量子即服务（Quantum-as-a-Service，QaaS）。QaaS 将量子计算作为一种云服务提供给用户，使得企业和个人能够以较低的成本和更灵活的方式利用量子计算的优势。让我们一同深入了解 QaaS 的概念、优势、挑战以及其对未来量子计算商业化的深远影响。

一、量子即服务（QaaS）的概念

12.2.1 什么是量子即服务？

量子即服务（QaaS）是一种云计算服务模式，它将量子计算资源作为一种服务提供给用户。用户可以通过互联网访问量子计算硬件和软件，而无需购买和维护昂贵的量子硬件设备。

12.2.2 QaaS 的服务类型

QaaS 可以提供多种类型的量子计算服务，包括：

1. 量子硬件访问：

超导量子计算机： 例如，IBM Quantum System One。
离子阱量子计算机： 例如，Honeywell 的量子计算机。
光子量子计算机： 例如，Xanadu 的 Borealis。

2. 量子模拟器：

经典模拟器： 利用经典计算机模拟量子电路的行为。
混合模拟器： 结合经典计算和量子计算的优势，提供更高效的模拟。

3. 量子软件开发工具：

量子编程框架： 例如，Qiskit、Cirq、Q# 等。
量子编译器： 将高级量子算法编译成可执行的量子电路。
量子模拟工具： 模拟量子算法的行为，帮助开发者进行调试和优化。

4. 量子应用服务：

量子化学计算： 提供分子能量计算、化学反应模拟等服务。
量子机器学习： 提供量子神经网络、量子核方法等机器学习服务。
量子优化： 提供组合优化、整数分解等服务。

二、QaaS 的优势

12.2.3 降低进入门槛

成本效益： 用户无需购买昂贵的量子硬件设备，只需支付使用费用即可访问量子计算资源。
无需专业知识： QaaS 提供了用户友好的接口和工具，降低了用户使用量子计算的门槛。

12.2.4 灵活性与可扩展性

按需访问： 用户可以根据需要随时访问量子计算资源，无需担心硬件维护和升级。
弹性扩展： QaaS 提供商可以根据用户需求动态调整资源分配，满足不同规模的应用需求。

12.2.5 加速创新与研发

快速原型开发： QaaS 允许用户快速构建和测试量子算法原型，加速创新过程。
协作与共享： QaaS 平台可以促进用户之间的协作和资源共享，推动量子计算技术的发展。

12.2.6 降低风险

硬件风险： 用户无需承担量子硬件的维护和更新风险，这些风险由 QaaS 提供商承担。
技术风险： QaaS 提供商通常会提供最新的量子计算技术，用户可以及时利用最新的研究成果。

三、QaaS 的挑战

12.2.7 量子硬件的限制

量子比特数量有限： 当前的量子硬件还处于早期阶段，量子比特数量有限，难以处理大规模问题。
相干时间短： 量子比特的相干时间较短，影响了量子计算的可靠性。
错误率高： 量子门操作的错误率较高，需要强大的量子纠错技术。

12.2.8 性能瓶颈

经典-量子接口： 经典计算与量子计算之间的数据传输和通信速度可能成为瓶颈。
资源调度： 有效地调度和管理量子计算资源是一个挑战。

12.2.9 安全性与隐私

数据安全： 用户的数据在传输和存储过程中需要得到保护，防止泄露和篡改。
量子安全： 量子计算对现有的加密算法构成威胁，需要开发新的量子安全加密方法。

12.2.10 标准化与互操作性

缺乏标准： 量子计算领域缺乏统一的标准，导致不同平台之间的互操作性差。
生态系统发展： 需要建立完善的量子计算生态系统，包括硬件、软件、服务等。

四、QaaS 的商业模式

12.2.11 订阅模式

用户按月或按年支付订阅费用，以获得对量子计算资源的访问权限。这种模式类似于 SaaS（软件即服务）模式。

12.2.12 按使用量付费

用户根据实际使用的量子计算资源（例如，量子比特数量、量子门操作次数、计算时间等）支付费用。这种模式提供了更大的灵活性，但成本可能更高。

12.2.13 混合模式

结合订阅模式和按使用量付费模式，用户可以选择最适合自己需求的付费方式。

12.2.14 定制化服务

为特定行业或应用场景提供定制化的量子计算解决方案，例如，金融服务、医疗保健、材料科学等。

五、QaaS 的应用场景

金融服务： 例如，期权定价、风险分析、投资组合优化等。
医疗保健： 例如，药物发现、基因组分析、个性化医疗等。
材料科学： 例如，新材料设计、催化剂开发、电池技术等。
化学与能源： 例如，化学反应模拟、能源系统优化等。
人工智能： 例如，量子机器学习、量子神经网络等。

六、QaaS 的未来展望

技术进步： 随着量子硬件技术的进步，QaaS 的性能将不断提高，应用范围将不断扩大。
生态系统发展： 量子计算生态系统将逐渐成熟，QaaS 提供商将提供更丰富的服务，例如，量子安全服务、量子应用开发平台等。
市场扩大： 越来越多的企业和机构将采用 QaaS，推动量子计算的商业化进程。
新商业模式： 新的商业模式将不断涌现，例如，量子计算即插即用服务、量子计算咨询服务等。

七、总结

在本节中，我们深入探讨了量子即服务（QaaS）：

概念： QaaS 将量子计算作为一种云服务提供给用户。
服务类型： 量子硬件访问、量子模拟器、量子软件开发工具和量子应用服务是 QaaS 的主要服务类型。
优势： 降低进入门槛、灵活性与可扩展性、加速创新与研发以及降低风险是 QaaS 的主要优势。
挑战： 量子硬件的限制、性能瓶颈、安全性与隐私以及标准化与互操作性是 QaaS 面临的主要挑战。
商业模式： 订阅模式、按使用量付费、混合模式和定制化服务是 QaaS 的主要商业模式。
应用场景： QaaS 在金融服务、医疗保健、材料科学、化学与能源和人工智能等领域具有广泛应用。
未来展望： 随着技术进步和生态系统发展，QaaS 的未来充满希望，将推动量子计算的商业化进程。

QaaS 是量子计算商业化的重要途径，它为用户提供了访问量子计算资源的便捷方式。通过学习和掌握 QaaS 的知识，您可以更好地了解量子计算的商业化趋势，并为未来的量子计算应用做好准备。

总而言之，QaaS 是量子计算的重要组成部分，它为我们提供了一种全新的商业模式，使得量子计算的应用更加广泛和便捷。希望这段旅程能够激发您对 QaaS 的兴趣，并为您的量子计算学习之旅提供一些启示。

12.3 安全通信协议：量子密钥分发的商业部署

欢迎来到量子云平台章节的最后一节。在前两节中，我们探讨了AWS Braket和量子即服务（QaaS），它们展示了量子计算与云计算融合的巨大潜力，以及量子计算商业化的新模式。在本节中，我们将深入探讨量子计算在信息安全领域的应用，特别是量子密钥分发（Quantum Key Distribution, QKD）。QKD 利用量子力学的独特特性来实现安全通信，其安全性基于量子力学的基本原理，而不是依赖于计算复杂性假设。让我们一同深入了解 QKD 的原理、商业部署现状及其在信息安全领域的革命性影响。

一、量子密钥分发的背景与动机

12.3.1 经典加密的局限性

对称加密： 例如，AES（高级加密标准），其安全性依赖于密钥的保密性，但密钥的分发是一个难题。
非对称加密： 例如，RSA（基于大整数分解）和 ECC（椭圆曲线加密），其安全性依赖于数学难题（例如，整数分解、离散对数问题）的计算难度。然而，量子计算对这类加密算法构成了巨大威胁，因为 Shor 算法可以在多项式时间内破解它们。

12.3.2 量子计算对信息安全的挑战

Shor 算法： 能够在多项式时间内分解大整数和求解离散对数问题，从而破解 RSA 和 ECC 等加密算法。
Grover 算法： 可以将对称加密算法的暴力破解速度提高平方倍，但可以通过增加密钥长度来缓解。

12.3.3 量子密钥分发的提出

为了应对量子计算对信息安全的挑战，科学家们提出了量子密钥分发（QKD）技术。QKD 利用量子力学的特性来实现安全密钥分发，其安全性基于量子力学的基本原理，而不是依赖于计算复杂性假设。

二、量子密钥分发的基本原理

12.3.4 量子力学的基本原理

QKD 的安全性基于以下量子力学基本原理：

量子叠加性： 量子态可以处于多个状态的叠加中。
量子测量干扰： 对量子态的测量会不可避免地改变其状态。
量子不可克隆定理： 量子态不能被完美复制。

12.3.5 BB84 协议

BB84 协议是第一个 QKD 协议，由查尔斯·贝内特（Charles H. Bennett）和吉勒斯·布拉萨德（Gilles Brassard）在 1984 年提出。其基本思想是利用量子态的不可克隆性和测量干扰来实现安全密钥分发。

协议步骤：

1. 量子态传输：

爱丽丝（发送者）随机生成一组比特串（例如，0101）。
爱丽丝随机选择一组量子态（例如，水平偏振 ∣H⟩、垂直偏振 ∣V⟩、45 度偏振 ∣+⟩ 和 135 度偏振 ∣−⟩）。
爱丽丝将每个比特编码到相应的量子态上，并将其发送给鲍勃（接收者）。

2. 测量：

鲍勃随机选择测量基（例如，水平和垂直或 45 度和 135 度）来测量接收到的量子态。
鲍勃记录测量结果，但不会立即公布测量基。

3. 密钥筛选：

爱丽丝和鲍勃通过经典信道公开交流他们使用的测量基，但不会透露测量结果。
对于那些鲍勃使用与爱丽丝相同的测量基的情况，测量结果可以作为密钥的一部分。

4. 密钥生成：

爱丽丝和鲍勃根据筛选结果生成密钥。
例如，如果爱丽丝发送的是∣H⟩ 或∣V⟩，而鲍勃使用水平和垂直基进行测量，则测量结果可以作为密钥的一部分。

5. 安全性检测：

爱丽丝和鲍勃通过比较部分密钥来检测是否存在窃听行为。
由于任何窃听行为都会改变量子态，从而导致测量结果的错误，因此可以检测到窃听。

12.3.6 安全性分析

不可克隆定理： 任何窃听者都无法完美复制量子态，因此无法窃取密钥而不被发现。
测量干扰： 任何对量子态的测量都会改变其状态，从而导致密钥分发过程中的错误。
信息理论安全性： QKD 的安全性不依赖于计算复杂性假设，而是基于量子力学的基本原理，因此被认为是信息理论安全的。

三、量子密钥分发的商业部署

12.3.7 商业 QKD 系统

近年来，许多公司已经开发了商业化的 QKD 系统，例如：

ID Quantique（瑞士）： 提供了多种 QKD 产品，例如，Clavis 系列，用于金融、政府和数据中心的安全通信。
Toshiba（日本）： 推出了基于光纤的 QKD 系统，例如，Toshiba QKD System，用于构建安全的量子网络。
QuantumCTek（中国）： 开发了多种 QKD 产品，例如，QKD-100，用于金融、政府和军事通信。

12.3.8 量子密钥分发的应用场景

金融行业： 银行、证券公司和保险公司可以利用 QKD 来保护敏感数据，例如，交易信息、客户数据等。
政府与军事： 政府机构和军事部门可以利用 QKD 来保护机密信息和通信安全。
数据中心： 数据中心可以利用 QKD 来保护数据存储和传输的安全。
关键基础设施： 例如，能源网络、交通系统等可以利用 QKD 来防止网络攻击。

12.3.9 量子密钥分发的挑战

传输距离： 目前的 QKD 系统主要基于光纤，传输距离有限，通常在几十到几百公里。
量子中继器： 为了实现长距离 QKD，需要开发可靠的量子中继器。
成本： 商业化的 QKD 系统目前成本较高，限制了其广泛应用。
标准化： QKD 技术的标准化工作仍在进行中，需要建立统一的标准来促进其发展。

12.3.10 未来展望

技术进步： 随着量子通信技术的发展，QKD 的传输距离将不断延长，成本将逐渐降低。
量子网络： 未来，QKD 将成为量子网络的重要组成部分，实现全球范围内的安全通信。
量子互联网： 量子互联网将整合 QKD、量子计算和量子传感等量子技术，为用户提供更强大的安全通信和计算能力。

四、总结

在本节中，我们深入探讨了量子密钥分发（QKD）：

背景与动机： 经典加密算法面临量子计算的威胁，QKD 提供了一种安全的密钥分发方案。
基本原理： QKD 利用量子力学的特性，例如，量子叠加性、测量干扰和不可克隆定理，来实现安全密钥分发。
BB84 协议： 详细介绍了 BB84 协议的步骤和安全性分析。
商业部署： 讨论了商业 QKD 系统的现状、应用场景、挑战和未来展望。

QKD 是量子计算在信息安全领域的革命性应用，它为实现安全通信提供了一种全新的方法。通过学习和掌握 QKD 的知识，您可以更好地理解量子计算在信息安全中的应用，并为未来的量子计算研究提供重要的参考。

总而言之，QKD 是量子计算的重要组成部分，它利用量子力学的独特特性，为我们提供了一种安全通信的新途径。希望这段旅程能够激发您对量子通信的兴趣，并为您的量子计算学习之旅提供一些启示。

第五部分：量子未来篇

第13章量子展望

量子优越性之后：实用量子计算机的工程悬崖
量子互联网蓝图：纠缠分发网络的星际迷航
后量子密码学：抗量子攻击的数学新防线
量子伦理困境：算力垄断与文明级安全危机

13.1 量子优越性之后：实用量子计算机的工程悬崖

欢迎来到量子展望的章节。在前面的章节中，我们探讨了量子计算的基本原理、算法、硬件架构、软件开发以及量子计算在各个领域的应用潜力。然而，量子计算从理论到实际应用的道路并非一帆风顺。在本节中，我们将深入探讨量子计算领域一个重要的里程碑——量子优越性，以及在实现实用量子计算机过程中面临的巨大挑战和“工程悬崖”。让我们一同深入了解量子计算的未来发展方向，以及我们距离真正实用的量子计算机还有多远。

一、量子优越性：量子计算的第一个里程碑

13.1.1 什么是量子优越性？

量子优越性（Quantum Supremacy）是指量子计算机在特定任务上超越最强大的经典超级计算机的能力。这个概念最早由加州理工学院的物理学家约翰·普雷斯基尔（John Preskill）在2012年提出。

13.1.2 量子优越性的实现

2019年10月，谷歌的研究团队在《Nature》杂志上发表论文，声称其量子处理器“悬铃木”（Sycamore）实现了量子优越性。该处理器包含53个量子比特，在200秒内完成了一项复杂的随机量子电路采样任务，而谷歌估计，使用目前最强大的超级计算机完成同样的任务需要1万年。

13.1.3 量子优越性的意义

理论证明： 量子优越性的实现证明了量子计算在某些特定任务上具有超越经典计算的能力。
技术突破： 量子优越性的实现标志着量子计算技术取得了重大突破，激励着科学家们继续探索量子计算的应用。
挑战与质疑： 量子优越性的实现也引发了关于其实际意义的讨论，例如，量子优越性任务是否具有实际应用价值，以及量子计算机是否能够解决实际问题。

二、实用量子计算机：量子计算的未来目标

13.1.4 什么是实用量子计算机？

实用量子计算机是指能够解决实际问题的量子计算机，其性能要超越经典计算机，并能够稳定可靠地执行量子算法。

13.1.5 实用量子计算机的特征

足够多的量子比特： 能够处理实际应用所需的问题规模。
高保真度的量子门操作： 量子门操作的错误率足够低，以保证计算的准确性。
长相干时间： 量子比特的相干时间足够长，以保证量子计算的可靠性。
量子纠错能力： 能够实现量子纠错，以克服退相干和量子错误的影响。
可扩展性： 能够实现大规模集成，以满足实际应用的需求。

13.1.6 实用量子计算机的应用

密码学： 破解现有的加密算法，例如，RSA 和 ECC，并实现量子安全加密。
材料科学： 模拟复杂的量子系统，例如，分子结构和化学反应，加速新材料的设计。
药物设计： 模拟药物分子与靶标的相互作用，加速药物发现和开发。
人工智能： 加速机器学习算法的训练，提高人工智能的性能。
优化问题： 解决复杂的组合优化问题，例如，旅行商问题、图着色问题等。

三、实用量子计算机面临的挑战

13.1.7 量子硬件的挑战

量子比特数量： 目前的量子硬件还处于早期阶段，量子比特数量有限，难以处理大规模问题。
相干时间： 量子比特的相干时间较短，影响了量子计算的可靠性。
错误率： 量子门操作的错误率较高，需要强大的量子纠错技术。
可扩展性： 将大量量子比特集成在一起，并实现精确的控制和测量，是一个巨大的挑战。

13.1.8 量子纠错的挑战

量子纠错码： 设计高效的量子纠错码是一个复杂的任务，需要在资源消耗和纠错能力之间进行权衡。
资源消耗： 量子纠错需要消耗大量的量子比特和量子门操作，增加了量子计算的复杂性。
实现难度： 在实际的量子硬件上实现量子纠错是一个巨大的挑战。

13.1.9 量子软件与算法的挑战

量子算法开发： 开发适用于量子计算机的算法是一个新兴领域，需要克服许多理论和技术挑战。
量子-经典混合算法： 开发有效的量子-经典混合算法，以充分利用经典计算和量子计算的优势。
量子编程框架： 开发功能强大、易于使用的量子编程框架和工具，以支持量子算法的开发和实现。

13.1.10 量子-经典接口的挑战

数据传输： 经典计算与量子计算之间的数据传输速度需要足够快，以避免瓶颈。
控制精度： 对量子比特的控制需要达到极高的精度，以保证量子计算的准确性。
同步性： 经典计算和量子计算之间的同步性需要得到保证，以确保计算的正确性。

四、跨越工程悬崖：实现实用量子计算机的路径

13.1.11 硬件改进

新材料与器件： 开发新的量子比特材料和器件，例如，拓扑量子比特、超导量子比特的新设计等。
低温技术： 改进低温制冷技术，例如，开发更高效的稀释制冷机，以延长量子比特的相干时间。
集成技术： 开发新的集成技术，例如，三维集成技术，以实现更大规模的量子比特集成。

13.1.12 量子纠错技术

新型量子纠错码： 探索新型量子纠错码，例如，拓扑量子纠错码，以降低资源消耗和提高纠错效率。
容错量子计算： 研究容错量子计算技术，例如，容错量子门操作，以实现更可靠的量子计算。

13.1.13 量子算法与软件

量子算法研究： 加大对量子算法研究的投入，开发适用于不同应用领域的量子算法。
量子编程框架： 开发更强大的量子编程框架和工具，例如，支持混合量子-经典编程、量子模拟和量子调试等。
量子软件开发工具包（SDK）： 提供功能丰富的 SDK，例如，Qiskit、Cirq、Q# 等，以支持量子算法的开发和实现。

13.1.14 量子-经典协同计算

混合计算框架： 开发更高效的混合计算框架，例如，CPU+QPU 协同工作模式，以充分利用经典计算和量子计算的优势。
量子云计算： 探索量子云计算模式，例如，量子即服务（QaaS），以降低量子计算的使用门槛和成本。

五、总结

在本节中，我们深入探讨了量子优越性之后，实用量子计算机面临的挑战：

量子优越性： 量子优越性的实现证明了量子计算在某些特定任务上的优势，但也引发了关于其实际意义的讨论。
实用量子计算机的特征： 足够多的量子比特、高保真度的量子门操作、长相干时间、量子纠错能力和可扩展性是实用量子计算机的主要特征。
挑战： 量子硬件、量子纠错、量子软件与算法以及量子-经典接口是实现实用量子计算机面临的主要挑战。
跨越工程悬崖： 硬件改进、量子纠错技术、量子算法与软件以及量子-经典协同计算是实现实用量子计算机的关键路径。

实用量子计算机的实现是一个复杂的系统工程，需要克服许多技术和工程挑战。尽管目前我们还处于量子计算的早期阶段，但随着技术的不断进步和研究的深入，我们有理由相信，实用量子计算机的实现将不再是遥不可及的梦想。

总而言之，量子优越性之后，实用量子计算机的实现是量子计算发展的下一个重要目标，而跨越工程悬崖则是实现这一目标的关键。希望这段旅程能够激发您对量子计算未来发展的思考，并为您的量子计算学习之旅提供一些启示。

13.2 量子互联网蓝图：纠缠分发网络的星际迷航 —— 探索量子通信网络的未来愿景

欢迎继续深入量子展望的世界。在上一节中，我们探讨了量子优越性之后的挑战，以及实现实用量子计算机的工程悬崖。在本节中，我们将把目光转向另一个令人兴奋的领域——量子互联网。量子互联网是一个利用量子力学原理，特别是量子纠缠，来实现安全通信和分布式量子计算的网络。它被广泛认为是未来信息技术的革命性发展，将彻底改变我们通信、计算和感知世界的方式。让我们一同踏上这段探索之旅，了解量子互联网的蓝图、关键技术挑战以及其对人类社会的影响。

一、量子互联网的概念与愿景

13.2.1 什么是量子互联网？

量子互联网是一个利用量子力学原理构建的全球性网络，其核心是利用量子纠缠来实现安全通信、量子计算资源共享和分布式量子信息处理。

13.2.2 量子互联网的愿景

量子互联网的愿景是创建一个全新的互联网架构，能够：

实现无条件安全的通信： 利用量子密钥分发（QKD）等技术，实现信息理论级别的安全通信。
构建全球量子计算网络： 将世界各地的量子计算机连接起来，实现分布式量子计算和资源共享。
实现量子传感与测量： 利用量子纠缠实现超精确的传感和测量，例如，量子定位、量子时钟同步等。
推动科学前沿发展： 为量子物理学、量子化学、量子生物学等领域的研究提供新的工具和方法。

二、量子互联网的关键技术

13.2.3 量子纠缠分发

量子纠缠是量子互联网的基石。要实现全球范围的量子互联网，需要能够长距离分发量子纠缠。

纠缠光子对： 通过非线性光学过程（例如，参数下转换）生成纠缠光子对。
量子中继器： 为了克服光纤传输中的损耗，需要开发量子中继器来延长纠缠分发的距离。
- 量子存储器： 量子中继器的核心组件，用于存储和操控量子态。
- 纠缠交换： 通过纠缠交换实现长距离纠缠分发。

13.2.4 量子信道

光纤信道： 目前，量子通信主要依赖于光纤信道，但光纤传输损耗限制了传输距离。
自由空间信道： 利用卫星进行自由空间量子通信，可以实现更远距离的纠缠分发。
- 卫星量子通信： 例如，中国的“墨子号”量子科学实验卫星已经实现了千公里级的量子密钥分发。

13.2.5 量子网络协议

量子网络协议栈： 与经典互联网类似，量子互联网也需要开发相应的网络协议栈，包括：
- 物理层： 负责量子态的生成、传输和测量。
- 链路层： 负责量子纠缠的分发和管理。
- 网络层： 负责量子路由和量子中继。
- 传输层： 负责量子通信的可靠传输。
- 应用层： 负责提供量子通信服务，例如，QKD、量子隐形传态等。

13.2.6 量子网络节点

量子网络节点是量子互联网的基本组成部分，负责：

量子态生成与操控： 生成、操控和存储量子态。
量子纠缠分发： 分发量子纠缠态。
量子信息处理： 执行量子计算任务，例如，量子门操作、量子测量等。

三、量子互联网的应用

13.2.7 量子密钥分发（QKD）

无条件安全通信： QKD 利用量子纠缠和量子不可克隆定理，实现信息理论级别的安全通信。
量子安全网络： 将 QKD 与经典通信网络结合，构建量子安全网络，保护敏感信息的安全。

13.2.8 分布式量子计算

量子云计算： 将量子计算机连接成网络，实现量子计算资源的共享和分布式计算。
量子计算任务分配： 将复杂的量子计算任务分配到不同的量子计算机上执行，提高计算效率。

13.2.9 量子传感与测量

量子定位： 利用量子纠缠实现超精确的定位，例如，量子导航。
量子时钟同步： 利用量子纠缠实现超高精度的时钟同步，例如，量子钟。
量子成像： 利用量子纠缠实现超分辨率成像，例如，量子显微镜。

13.2.10 量子互联网的其他应用

量子隐形传态： 实现量子态的远程传输。
量子密码学： 开发新型量子密码协议，例如，量子秘密共享、量子安全多方计算等。

四、量子互联网的挑战

13.2.11 技术挑战

量子纠缠分发： 实现长距离、高保真度的量子纠缠分发是一个巨大的挑战。
量子中继器： 开发可靠的量子中继器是实现全球量子互联网的关键。
量子网络协议： 开发适用于量子网络的协议栈是一个新兴的研究领域。
量子网络节点： 构建功能强大、可靠的量子网络节点需要克服许多技术挑战。

13.2.12 安全挑战

量子安全： 量子计算对现有的加密算法构成威胁，需要开发新的量子安全加密方法。
量子网络攻击： 量子网络可能面临新的安全威胁，例如，量子黑客攻击，需要开发相应的防御机制。

13.2.13 标准化与互操作性

标准化： 量子互联网的标准化工作仍在进行中，需要建立统一的标准来促进其发展。
互操作性： 不同量子网络节点和系统之间的互操作性需要得到保证。

五、量子互联网的未来展望

技术进步： 随着量子通信技术的发展，量子互联网的关键技术将不断取得突破。
全球网络构建： 未来，量子互联网将逐步从实验室走向现实，构建全球范围的量子通信网络。
应用扩展： 量子互联网的应用将不断扩展，从量子密钥分发到分布式量子计算，再到量子传感与测量。
社会影响： 量子互联网将深刻影响人类社会，改变我们通信、计算和感知世界的方式。

六、总结

在本节中，我们深入探讨了量子互联网：

概念与愿景： 量子互联网是一个利用量子力学原理构建的全球性网络，旨在实现安全通信、分布式量子计算和量子传感。
关键技术： 量子纠缠分发、量子信道、量子网络协议和量子网络节点是构建量子互联网的关键技术。
应用： QKD、分布式量子计算、量子传感与测量是量子互联网的主要应用领域。
挑战： 技术挑战、安全挑战以及标准化与互操作性是量子互联网面临的主要挑战。
未来展望： 随着技术进步，量子互联网将从实验室走向现实，并深刻影响人类社会。

量子互联网是量子计算和量子通信发展的重要方向，它将为我们提供一种全新的通信和计算方式。通过学习和掌握量子互联网的知识，您可以更好地理解量子技术的未来发展方向，并为未来的量子计算研究提供重要的参考。

总而言之，量子互联网是量子技术的未来愿景，它利用量子纠缠的力量，为我们描绘了一幅星际迷航般的宏伟蓝图。希望这段旅程能够激发您对量子互联网的兴趣，并为您的量子计算学习之旅提供一些启示。

13.3 后量子密码学：抗量子攻击的数学新防线 —— 探索量子时代的安全密码学

欢迎继续深入量子展望的旅程。在前两节中，我们探讨了量子优越性之后的挑战以及量子互联网的蓝图，这些内容展示了量子计算和量子通信的革命性潜力。然而，量子计算的出现也带来了新的安全威胁，特别是对现有的密码学体系。在本节中，我们将深入探讨后量子密码学（Post-Quantum Cryptography, PQC），这是一门旨在开发能够抵抗量子计算攻击的密码学新领域的学科。让我们一同深入了解后量子密码学的背景、原理、挑战以及其对未来信息安全的影响。

一、量子计算对经典密码学的威胁

13.3.1 经典密码学概述

经典密码学主要依赖于以下两类加密算法：

1.对称加密算法：例如，AES（高级加密标准），加密和解密使用相同的密钥。

2.非对称加密算法：例如，RSA（基于大整数分解）和 ECC（椭圆曲线加密），加密和解密使用不同的密钥（公钥和私钥）。

13.3.2 量子计算的威胁

Shor 算法： 能够在多项式时间内分解大整数和求解离散对数问题，这使得 RSA 和 ECC 等非对称加密算法变得不再安全。
Grover 算法： 可以将对称加密算法的暴力破解速度提高平方倍，但可以通过增加密钥长度来缓解其影响。

13.3.3 经典密码学的脆弱性

非对称加密： 量子计算对 RSA、ECC 等非对称加密算法构成致命威胁，因为 Shor 算法可以有效地破解它们。
对称加密： 虽然 Grover 算法的影响相对较小，但仍然需要将密钥长度加倍（例如，从 128 位增加到 256 位）以保持相同的安全级别。

二、后量子密码学的目标

13.3.4 什么是后量子密码学？

后量子密码学是指设计能够抵抗量子计算攻击的密码学算法和协议。其主要目标包括：

安全性： 即使面对量子计算机的攻击，后量子密码学算法仍然能够提供足够的安全性。
效率： 后量子密码学算法应该具有与经典密码学算法相当的计算效率。
兼容性： 后量子密码学算法应该能够与现有的通信协议和系统兼容。

三、后量子密码学的主要研究方向

13.3.5 基于格的理论（Lattice-Based Cryptography）

原理： 基于格问题的计算困难性，例如，最短向量问题（Shortest Vector Problem, SVP）和最近向量问题（Closest Vector Problem, CVP）。
优势： 安全性基于格问题的困难性，量子计算对这类问题的影响较小。
应用： 例如，格基加密、格基签名等。

13.3.6 基于编码理论（Coding-Theory-Based Cryptography）

原理： 基于纠错码的编码和解码问题的计算困难性。
优势： 一些编码问题被认为对量子计算具有抵抗力。
应用： 例如，McEliece 加密系统。

13.3.7 基于多变量多项式（Multivariate Polynomial Cryptography）

原理： 基于求解多变量多项式方程组的计算困难性。
优势： 一些多变量多项式问题被认为对量子计算具有抵抗力。
应用： 例如，Rainbow 签名方案。

13.3.8 基于哈希函数（Hash-Based Cryptography）

原理： 基于哈希函数的单向性和抗碰撞性。
优势： 一些基于哈希函数的方案，例如，Lamport 签名方案，被认为对量子计算具有抵抗力。
应用： 例如，量子安全的签名方案。

13.3.9 其他研究方向

基于同态加密（Homomorphic Encryption）： 允许对加密数据进行计算，而无需解密。
基于秘密共享（Secret Sharing）： 将秘密信息分割成多个部分，并分配给不同的参与者。

四、后量子密码学的挑战

13.3.10 安全性证明

挑战： 证明后量子密码学算法的安全性是一个复杂的任务，需要克服许多理论和技术挑战。
现状： 目前，大多数后量子密码学算法的安全性是基于计算复杂性假设，而不是信息理论安全性。

13.3.11 效率与性能

挑战： 后量子密码学算法通常比经典密码学算法更复杂，计算开销更大。
优化： 需要开发更高效的后量子密码学算法，并进行优化以提高其性能。

13.3.12 标准化与互操作性

挑战： 后量子密码学算法的标准化工作正在进行中，需要建立统一的标准以促进其应用。
互操作性： 不同后量子密码学算法之间的互操作性需要得到保证。

13.3.13 量子-经典混合攻击

挑战： 需要考虑量子-经典混合攻击的可能性，并设计相应的防御机制。

五、后量子密码学的应用

加密通信： 保护敏感数据的机密性，例如，电子邮件、文件传输等。
数字签名： 确保数据的完整性和真实性，例如，电子签名、代码签名等。
密钥交换： 实现安全密钥交换，例如，TLS 协议中的密钥交换。
身份认证： 实现安全的身份认证机制，例如，量子安全的身份认证协议。

六、后量子密码学的未来展望

技术进步： 随着研究的深入，后量子密码学算法将不断取得突破，安全性将不断提高。
标准化进程： 后量子密码学算法的标准化工作将逐步完成，为其广泛应用奠定基础。
实际应用： 后量子密码学算法将逐渐被集成到现有的安全协议和系统中，例如，TLS、SSH、PGP 等。
新密码学范式： 后量子密码学将推动密码学的发展，催生新的密码学范式，例如，量子密码学、量子安全多方计算等。

七、总结

在本节中，我们深入探讨了后量子密码学：

背景与动机： 量子计算对现有的密码学体系构成威胁，后量子密码学旨在开发能够抵抗量子攻击的密码学算法。
主要研究方向： 基于格的理论、基于编码理论、基于多变量多项式和基于哈希函数是后量子密码学的主要研究方向。
挑战： 安全性证明、效率与性能、标准化与互操作性和量子-经典混合攻击是后量子密码学面临的主要挑战。
应用： 后量子密码学在加密通信、数字签名、密钥交换和身份认证等领域具有广泛应用。
未来展望： 随着技术进步和标准化进程，后量子密码学将逐步走向实际应用，并推动密码学的发展。

后量子密码学是量子时代信息安全的重要防线，它为我们提供了一种抵御量子计算攻击的新方法。通过学习和掌握后量子密码学的知识，您可以更好地理解量子计算对信息安全的影响，并为未来的信息安全研究提供重要的参考。

总而言之，后量子密码学是量子计算时代密码学发展的新方向，它利用数学的力量，为我们提供了一种抵抗量子攻击的有效途径。希望这段旅程能够激发您对后量子密码学的兴趣，并为您的量子计算学习之旅提供一些启示。

13.4 量子伦理困境：算力垄断与文明级安全危机 —— 探讨量子计算带来的社会与伦理挑战

欢迎来到量子展望章节的最后一节。在前面的章节中，我们探讨了量子计算的技术发展、应用前景以及其对信息安全的深远影响。然而，量子计算作为一项颠覆性技术，其发展不仅仅局限于技术层面，还将带来一系列社会、伦理和安全方面的挑战。在本节中，我们将深入探讨量子计算可能引发的伦理困境，特别是算力垄断和文明级安全危机，并思考我们如何应对这些挑战，以实现量子技术的负责任发展。

一、量子计算与算力垄断

13.4.1 算力垄断的潜在风险