并行算法——双调排序

最新推荐文章于 2024-03-27 18:07:42 发布

原创最新推荐文章于 2024-03-27 18:07:42 发布 · 1.2k 阅读

4 ·

CC 4.0 BY-SA版权

并行算法专栏收录该内容

1 篇文章

订阅专栏

本文深入探讨双调序列的概念及其在排序算法中的应用。通过递归分治思想，将任意序列转化为双调序列，并利用BitonicSplit和BitonicMerge函数进行高效排序。分析了算法的复杂度，展示了其在并行计算中的优势。

$O(nlog^{2}n)$ Bitonic Sequences

首先来介绍一下什么叫做双调序列，我认为，这个序列是一个先增再减的序列(或者先减再增)，判断方法是这样滴，首先，将序列第一个元素和最后一个元素连一条线，构成一个环，然后计算每条线的增减性，如果是下面这样的序列，就可以叫做Bitonic Sequences，在算法中，通常要求长度是2**k

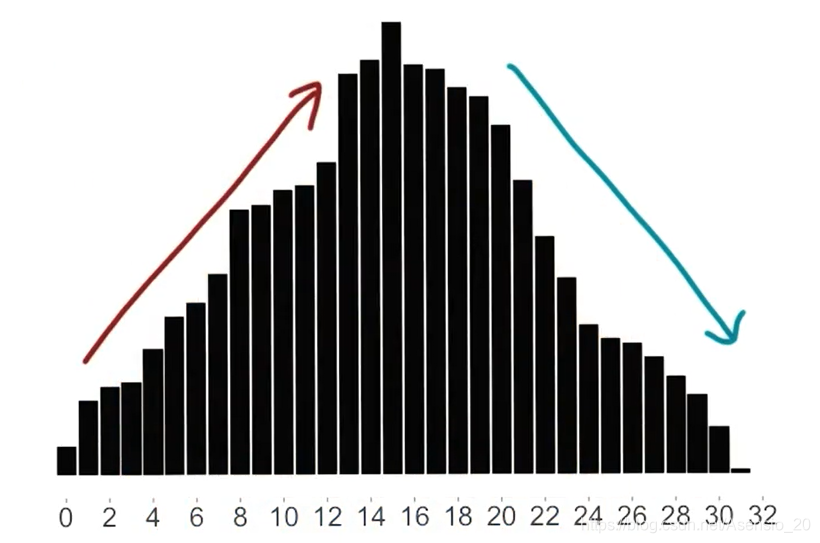
再举个简单的例子：

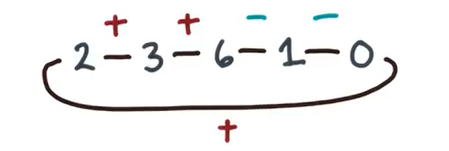
好了，这就是双调排序的基础，下面我们来看一下如何利用这种双调序列

Bitonic Split

这一步做了什么呢，其实很简单，就是将一个双调序列分成两个双调序列

怎么分呢，

$A[0]=min(A[0],A[\frac{n}{2}])$

$A[\frac{n}{2}] = max(A[\frac{n}{2}], A[0])$

这样，就形成了一个 $[0, \frac{n}{2})$ 的双调序列和一个 $[\frac{n}{2}, n)$ 的双调序列，如下图所示

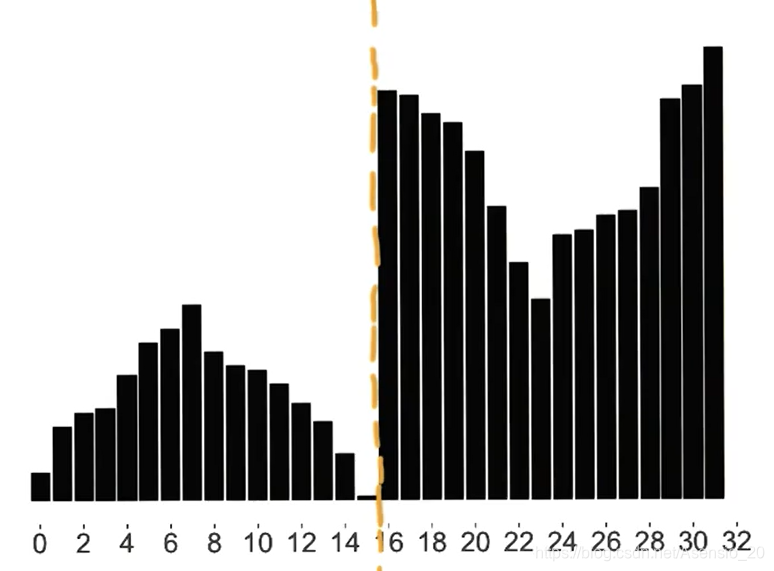
且你会发现左边的最大值会小于等于右边的最小值，这就为我们实现并行提供了基础：左右同时计算即可

Bitonic Merge

这个就是那个排序的函数了，伪代码也比较好写

void BitnoicMerge(A[0..n-1])
{
    //要求n是偶数
    if(n>=2)
    {
         BitnoicSplit(A[0..n-1]);
         BitnoicMerge(A[0..n/2-1]); //这两个BitnoicMerge是可以并行执行的
         BitnoicMerge(A[n/2..n-1]);
    }

}

可是，一般序列都是任意的，我们怎么样把它转化成一个双调序列呢？

How to form a Bitonic Sequence

这里我们也是用了一下递归分治的思想，你想啊，如果一个序列前半段是增序列，后半段是减序列，那么这个序列不就是一个双调序列了么，且如果一个序列的size是2，他也是一个双调序列

伪代码如下：

void genBitonic(A[0..n-1])
{
    genBitonic(A[0..n/2-1]);
    genBitonic(A[n/2..n-1]);

    BitonicMerge_add(A[0..n/2-1]);
    BitonicMerge_minus(A[n/2..n-1]); //前半段增序后半段降序，这不就是一个双调序列么，可是这个函数只能处理双调序列的排序，所以前面要有genBitonic
}

复杂度分析

该算法串行时间复杂度 $O(nlog^{2}n)$ ，span complexity是 $O(log^{2}n)$ , 分析过程如下

首先，我们可以看到，该算法主要的复杂度在genBitonic上面，那么这个过程是什么样的呢，可以通过下面这张图片来理解

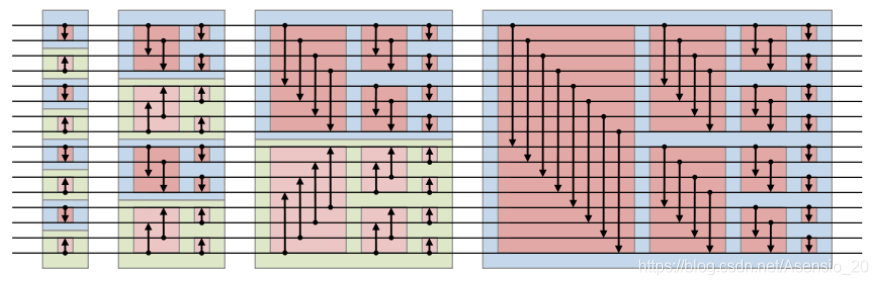
可以看到，其DAG图计算的span complexity为1+2+...+log n，即 $O(log^{2}n)$ ，这个span没有计算并行for循环的span，将其视作O(1)而不是O(log n)，至于work complexity呢，可以观察上图每一个span节点，其同阶段节点共有n/2个(因为两两比较)，然后就可以轻松计算出串行时间复杂度 $O(nlog^{2}n)$ 了，这个看图比较容易理解，看代码反而不容易理解了

至于BitonicMerge的时间复杂度啥的，可以通过上图的一个同色方框来理解，其span complexity是O(log n), work complexity是O(nlog n)