python基础 | 核心库：NumPy 矩阵计算

NumPy不是标准库，不是自带的，需要自己安装。要通过终端来安装，vs里面的不行
官方文档

1、创建

1.1 指定创建

import numpy as np
	
a = np.array([1,2,3]) # 创建数组(以列表方式)
                      # 注：asarray 和array类似，只是array会copy对象，而asarray必要时才copy
print(a)
print(a.shape)        # 查看形状  shape=(3,) 表示 一维数组 元素为3 
print(a.dtype)        # 查看元素类型
print(np.array([1,2,3],dtype = np.float64))  # 指定元素类型 np.float报错，人工智能运算是使用浮点型的

a = np.array([[1,2,3],
              [4,5,6]])   # 创建多维数组(用列表嵌套方式) 注意格式
print(a)
print(a.shape)            # shape=(2,3) 二维数组 2行3列

print(np.empty([3, 2]))   # 空数组创建  3行2列的空数组(不初始化值，给随机浮点值较快）
print(np.zeros([2, 3]))   # 0数组创建   2行3列的0数组(初值都为0，较慢）
print(np.arange(0,2,0.3)) # 按范围创建  0:开始值 2:终值  0.3:步长（默认为1）

运行结果

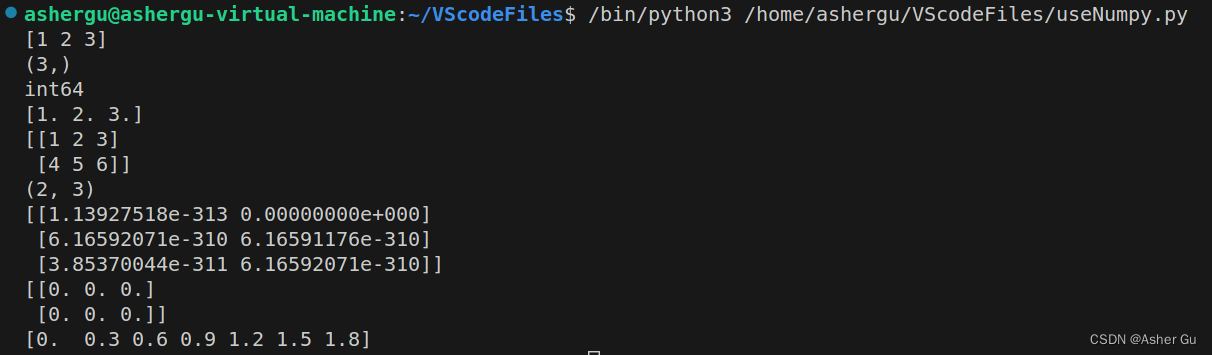
1.2 随机创建

np.random.seed(7)  # 设定随机数种子，保证结果的可重现性
# 当你设置了一个特定的种子后，每次运行程序时都会生成相同的随机数序列，这对于调试代码和实验复现是非常有用的

print(np.random.rand(3))  # 创建3个随机数,放在列表里面(范围0~1的浮点数)
print(np.random.random((5, 2)))  # 创建5行2列的随机数数组(数范围0~1浮点数）
print(np.random.randint(0, 10))  # 生成一个0到10以内(包括0，和10)的随机整数
print(np.random.randint(23, size=(3, 4))) # 创建3行4列的23以内整型随机数数组

运行结果

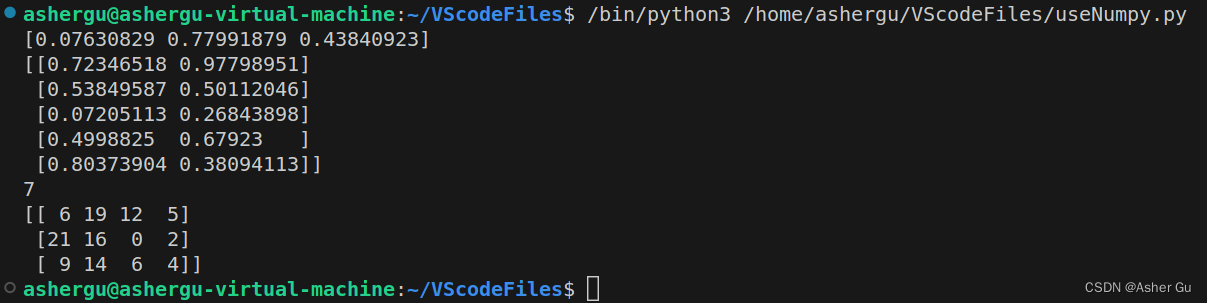
2、行列操作

2.1 行列选取二维数组元素

都是 从0开始算，步长指 每次前进几格
从 起始位置/终止位置、中间步长去跨、直接列表指定

a = np.array([[ 0, 1,   2,  3,  4, 5],
              [10, 11, 12, 13, 14, 15],
              [20, 21, 22, 23, 24, 25],
              [30, 31, 32, 33, 34, 35],
              [40, 41, 42, 43, 44, 45],
              [50, 51, 52, 53, 54, 55]])
print(a[1,3])        # 行(0轴)1 列(1轴)3 的值： [13]               
print(a[1,3:5])      # 行1 列(3~4)的值：    [13 14]
print(a[1,:5])       # 行1 列(开始~5)的值： [10 11 12 13 14]  
print(a[1,3:])       # 行1 列(3~结束)的值： [13 14 15] 	         
a[1,3:5] = [5,5]     # 把行1 列(3~5)的值 [13 14] 改为  [5,5]	
print(a[4:,4:])      # 行(4~end) 列(4~end) 的值
              # [[44 45]
	          # [54 55]]	
print(a[:,2])       # 列2  [ 2 12 22 32 42 52]
print(a[2])   	    # 行2  [20 21 22 23 24 25]
print(a[1::2,::3]) # 1:行号  2:行步长 3:列步长
	    # [[10 13]
	    # [30 33]
	    # [50 53]]
	            
print(a[4:,[0,2,5]]) # 行(4~end) 列0 2 5
	      # [[40 42 45]
	      #  [50 52 55]]

运行结果

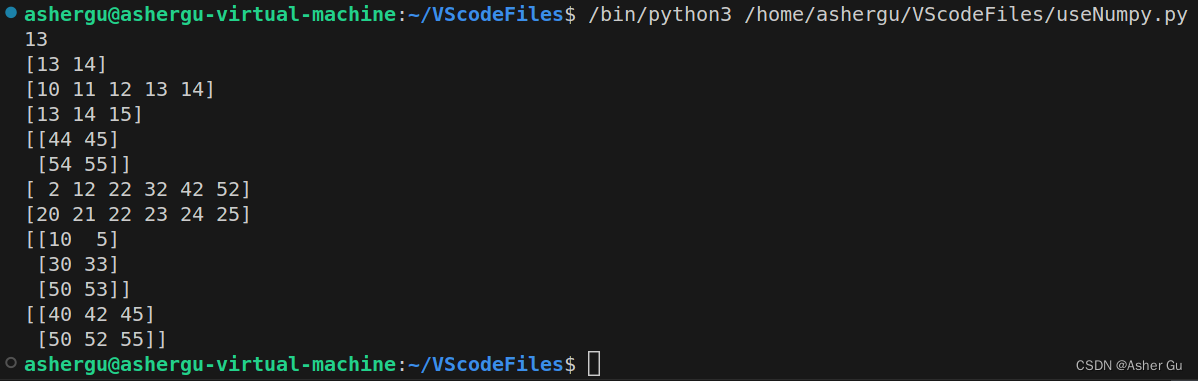
2.2 行列连接（行或列需匹配）

垂直水平拼接

a = np.array([[1, 2],
              [3, 4]])
b = np.array([[5, 6]])
print(np.vstack((a,b)))               # 垂直连接
print(np.concatenate((a, b), axis=0)) # 沿轴0连接(按行把b连接在a后面)，跟上面那个等价，只是表达方式不同
a = np.array([[1, 2],
              [3, 4]])
b = np.array([[11,12],
              [21,22]])
print(np.hstack([a,b]))               # 水平连接              
print(np.concatenate((a, b), axis=1)) # 沿轴1连接(按列把b连接在a后面)，跟上面那个等价，只是表达方式不同

运行结果

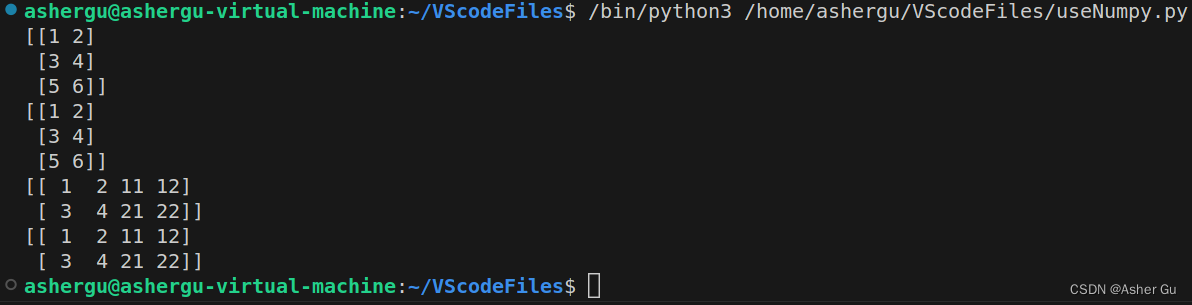
2.3 行列转换（维度变化）

如果不赋值 a.shape不改变原来的矩阵，除非 重新赋值给原来的矩阵

a = np.array([[1,2,3],    # 创建矩阵
              [4,5,6]])   
print(a, a.shape)  
a = a.reshape(3,-1)       
print(a, a.shape)   # 行列变化 -> 重新设置形状(行3，-1是让系统推导列， 原对象未改变）
                 # 1 2
		         # 3 4
		         # 5 6

运行结果

2.4 行列扩展（从数据角度没区别）

shape / ndim都是属性

x = np.array([1,2])
print(x.shape)
print(x.ndim)                  # 维度的个数( 维度即轴，如二维平面，行就是轴0(x轴),列是轴1(类似y轴))   
y = np.expand_dims(x, axis=0)  # 行拓展，沿轴0(行)扩展 -> 变为1行多列
print(y,y.shape,y.ndim)        # [[1, 2]] 
y = np.expand_dims(x, axis=1)  # 沿轴1(列)扩展 -> 变为1列多行
print(y,y.shape,y.ndim)		   # 相当于 [[1]
                               #        [2]]

运行结果

3、数组元素计算

3.1 加减乘除（行列数需一致）

都是对相同位置的元素 做计算

a = np.array([[7,8,9],
              [1,0,1]]) 
b = np.array([[1,2,3],
              [4,5,6]])
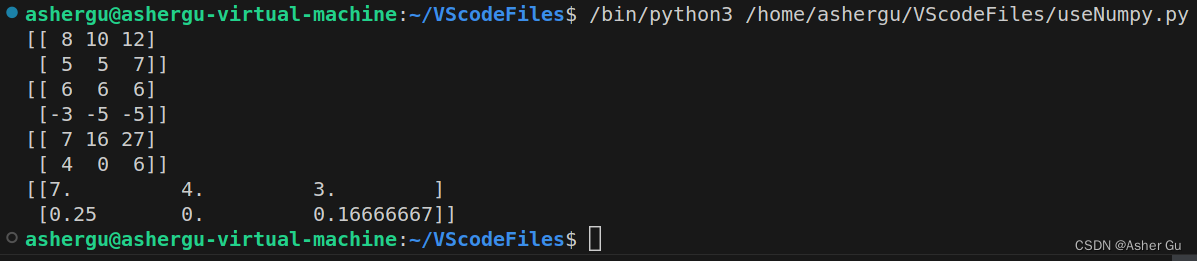
print(a+b)   # 对应位置的元素相加
             # 或用np.add(a,b) 
print(a-b)   # 对应位置元素相减
print(a*b)   # 对应位置元素相乘（注意：不是矩阵的乘法）
print(a/b)	 # 对应位置元素相除

运行结果

3.2 元素运算

a = np.array([[7,8,9],
              [1,0,1]]) 
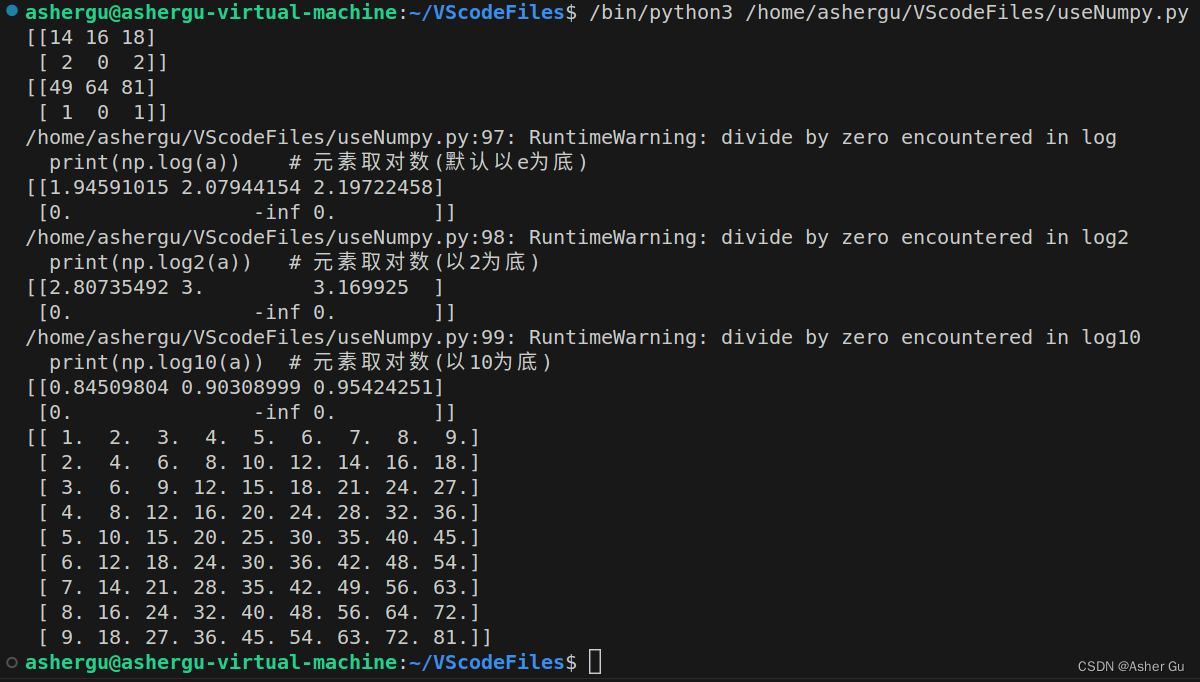
print(a*2)   # 元素都乘2
print(a**2)  # 元素都2次方
print(np.log(a))    # 元素取对数(默认以e为底)
print(np.log2(a))   # 元素取对数(以2为底)
print(np.log10(a))  # 元素取对数(以10为底)

# lambda函数，传入变量i,j，返回 (i+1)*(j+1)
a = np.fromfunction(lambda i,j:(i+1)*(j+1), (9,9)) # 按某函数处理数组元素 -> 九九乘法表 i:行号 j:列号 
print(a)

运行结果

np.fromfunction：
根据指定的函数创建一个数组。这个函数接受一个函数对象和一个表示数组维度的元组作为参数，然后使用指定的函数来计算数组中每个元素的值

np.fromfunction(function, shape, **kwargs)

function：一个函数对象，用于计算数组中每个元素的值。这个函数将被调用，并传递每个元素的索引作为参数，返回值将被放入相应位置的数组中
shape：一个表示所需数组的形状的元组。每个维度的大小决定了数组中该维度的元素数量
**kwargs：可选的额外参数，用于传递给函数对象

import numpy as np

def sum_of_indices(x, y):
    return x + y

array = np.fromfunction(sum_of_indices, (3, 3))
print(array)

产生以下输出
[[0. 1. 2.]
[1. 2. 3.]
[2. 3. 4.]]

3.3 行列合并（降维）

比如彩色的图片 降维 进行信息压缩，保证特征不变的情况下加快速度

a = np.array([[1,2,3],
              [4,5,6],
              [6,7,8]])
print(np.add.reduce(a))  # 缩减(按add回调函数方式)降维[11 14 17] 按行求和方式，把三行矩阵变为一行
print(np.mean(a))        # 求平均值（降成1个数了）  
print(np.mean(a[1]))     # 求行1的平均值
print(np.sum(a))         # 累加和

运行结果

3.4 最值位置选取（降维）

也是信息的压缩

a = [3, 1, 2, 6, 1]
np.argmax(a)                # 最大值位置 3 (a[3]的6最大) 
a = np.array([[1, 5, 5, 2],
              [9, 6, 2, 8],
              [3, 7, 9, 1]])
print(np.argmax(a, axis=0)) # 按行(0轴)纵向去找 找最大值位置 [1,2,2,1]
print(np.argmax(a))         # 总体最大值（第4个一行一行数）
print(np.argmax(a, axis=1)) # 按列(1轴)横向去找 找最大值位置 [1,0,2]

运行结果

4、矩阵运算

4.1 矩阵转置

a = np.array([[1,2,3],
              [4,5,6]])
print(a.T)  # 局限于2维矩阵转置 
            # [[1 4]
	        #  [2 5]
	        #  [3 6]]
 
print(a.transpose()) # 可多维矩阵转置

运行结果

4.2 矩阵乘法（行列需匹配）

线性拟合

x = np.array([[1, 2, 3], 
              [4, 5, 6]])
w = np.array([[1,2], 
              [3,4],
              [5,6]])
print(np.dot(x,w)) # 矩阵乘法(dot会把数组看成矩阵做乘法运算)
#  xw= |1,2,3| |1 2|
#      |4,5,6| |3 4|  
#              |5 6|   
#   =  1*1+2*3+3*5  1*2+2*4+3*6
#      4*1+5*3+6*5  4*2+5*4+6*6 
#   = [[22 28]
#      [49 64]]
        
x = np.array([[1,2,3],   # x1 x2 x3 创建矩阵
              [4,5,6]])  # z1 z2 z3
w = np.array([[3],       # w1=3 权值
              [1],       # w2=1 权值
              [2]])      # w3=2 权值
                     
b = np.array([[2],       # b1=2 偏置（去除坐标系影响，只考虑彼此的相对位置）
              [2]])      # b2=2
              
print(np.dot(x,w)+b)     # 矩阵混合运算 x*w+b 
                         # y=x*W+b  =  |1,2,3||3|    |2| 
                         #             |4,5,6||1|  + |2|
                         #                    |2| 
		                 #y=x*W+b  =  x1*w1+x2*w2+x3*w3 + b1 =1*3+2*1+3*2 + 2 = 13     
		                 #		      z1*w1+z2*w2+z3*w3 + b2 =4*3+5*1+6*2 + 2 = 31

运行结果