软件测试-黑盒测试：正交实验设计法

正交实验设计法

参考文献：
测试用例设计方法–正交试验法详解
正交试验设计方法(详细步骤)
正交试验软件测试用例设计方法

正交表是一种特制的表格，一般用$L_n(m^k)$表示，L代表是正交表，n代表测试用例的个数（正交表的行数），k代表最多可安排影响指标因素的个数（正交表的列数），m表示每个因素水平数（因素的取值个数），且有$n=k\ast (m-1)+1$。
目的：利用正交表来对试验进行设计，通过少数的试验替代全面试验，具备“均匀分散，整齐可比”的特点。
特点：表中任一列，不同数字出现的次数相同；表中任意两列，各种同行数字对出现次数相同。
例题：某被测工程数据库查询语言软件由规格说明书得到的因子-状态表如图所示：

1. 提取功能说明，构造因子—状态表（就是上图）
   在本题中，共有k=4个因子，m=3个状态
2. 加权筛选，生成因素分析表
   
   加权筛选后，共有k=3个因子，m=3个状态
3. 利用正交表构造测试数据集
   正交表中，每列表示一个因子，每行表示一个项目。
   
   
   
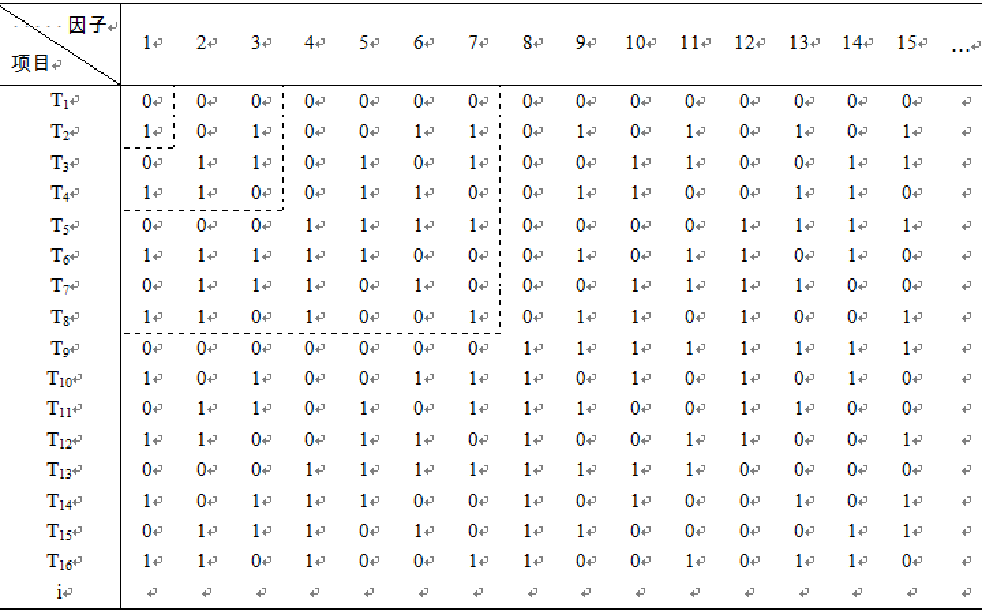
   三种情况：
   第一种情况：因子的状态数正好和正交表的状态数相等，那么此时只需要直接替换正交表中的值即可。
   第二种情况：因子的状态数多于正交表中的状态数，那么此时需要先将多余的状态合并，带入正交表中，然后再将合并的中间状态展开。
   第三种情况：因子的状态数少于正交表中的状态数，那么只要将正交表中多出来的状态，使用实际状态
   将因素分析表中各因子的状态作为输入，结果作为输出，用逻辑命令把输入与输出结合4在一起，画出布尔图。（两两一组）
   
   
   上表是如何变到下表的，我想了一晚上，其实核心非常简单，就是：等价代换。
   我觉得如果把上表的B1->B12后，可能会更好理解。因为B12对应两个节点，所以应该加以展开。
   展开方法：当B12=1时，用一个小的正交表替换，其余列复制即可。