NSST: Non-Separable Secondary Transforms for Next Generation Video Coding

摘要—在传统的图像和视频编码方案中，由于可分离变换复杂度较低，通常采用可分离的变换。然而，对于通常大多数具有任意定向的边缘和纹理图案的自然图像/视频块，可分离变换的压缩效率受到限制。众所周知，对于具有方向性的纹理图案，不可分离的变换可以实现更好的压缩效率，但是它们的计算复杂，尤其是对于较大的块而言。为了用相对低复杂度的实现方式实现更高的变换编码增益，在本文中，我们提出了不可分离的二次变换（NSST）。所提出的方法将二次不可分变换应用于使用主可分变换（例如离散余弦变换（DCT））生成的低频系数的子块上。由于建议的NSST是不可分离的变换，它以较小的块大小应用于低频系数，通常捕获大部分信号能量，因此可以以较低的计算成本获得更好的编码增益。实验结果表明，与最新的HEVC参考软件（HM16.6）相比，所提出的方法可实现高达12％的有效帧内编码增益。

一、INTRODUCTION

在H.264/AVC[1]、VP9[2]和HEVC[3]等几种主流视频编码标准中广泛采用的基于块的混合视频编码结构中，变换编码对于获得可观的视频压缩比起着至关重要的作用。虽然典型的预测过程只会减少当前块数据中参考像素和像素之间的统计冗余，但是对于变换过程来说，进一步消除残差样本之间的像素间冗余是非常重要的，这样熵编码过程可以更好地去相关变换系数。

最近，在国际视频标准化会议上，探索下一代视频编码技术的活动正在升温。具体来说，在2015年1月ITU-T SG16/Q6 VCEG会议上，在HEVC参考软件的基础上提出了几种新的编码工具。使用所提出的新编码工具，可以获得10%的显著编码增益。该编解码器被用作探索未来视频编码技术的公共平台，即HM-KTA。随后于2015年6月在华沙召开的VCEG会议上，在HM-KTA的基础上提出了新的编码工具，并进一步提高了整体编码增益。之后，在2015年10月的ITU-T SG16/Q6 VCEG和ISO/IEC JTC1 SC29WG11 MPEG会议上，VCEG和MPEG联合成立了一个探索未来视频编码技术的联合团队，即JVET，并将HM-KTA的开发改为联合探索模式（JEM）。在JEM中所有现有的增强工具中，变换设计成为一个特别有趣的话题，因为只带来与变换相关的新设计[5][6]实现了显著的编码增益。

在文献中，在过去的半个世纪里，各种变换方案都得到了发展，DCT-2变换成为图像和视频编码应用中最受欢迎的解决方案。 它在变换效率和计算复杂性之间的平衡出色。理论和实验证明，在一阶平稳马尔可夫条件下，相关矩阵是Toeplitz矩阵时，DCT-2在能量压缩效率方面非常接近最佳变换（即Karhunen Lo -ε变换）[7][8][9]。但是， 自然视频信号通常呈现高度动态的统计数据，如边缘、曲线和方向纹理，而一阶平稳马尔科夫不能简单地对其进行有效的模拟。

为了提高变换过程的适应性，文献中提出了多种方向自适应变换方案。一个值得注意的突破是方向小波基的发明[10]，例如所谓的脊波变换[11]、曲线变换[12]和轮廓波变换[13]。然而，这些基于小波的变换主要用于去噪。在传统的基于块的残差图像/视频编码的情况下，文[14]提出了一种方向二维可分离DCT方法。与传统的水平和垂直应用一维离散余弦变换的二维可分离离散余弦变换不同，在文献[14]中，第一个一维离散余弦变换是沿着预先定义的方向之一而不是0度或90度应用的，然后将DC变换系数对齐，并沿垂直方向执行第二个一维离散余弦变换。在H.264/AVC的基础上，在文献[15]中提出了一种模式相关的方向变换，利用离线训练的KLTs来提高每个帧内预测模式的变换效率。此外，为了进一步改进与模式相关的变换设计，提出了一种速率失真优化变换[16][17]。针对HEVC的帧内编码，在[20]中提出了一种与模式相关的可分离二次变换。

最近，有一些新的努力方向[18][19]试图在HEVC之上实现不可分离变换。为帧内编码获得了高达12%的编码增益，但沉重的编码器和解码器的复杂负担使得不可分离的变换对于实际的视频编解码器让人怀疑。本文提出了一种不可分离二次变换（NSST）方法，该方法只需要小尺寸的不可分离变换就可以获得显著的编码增益。该算法大大降低了对较大残差块应用不可分离变换的计算量。所提出的NSST已被作为JEM中主要的变换编码工具之一。

本文的其余部分安排如下：第二节对不可分变换作了简要的评述。在第三节中，描述了NSST的技术细节。第四节对实验结果进行了讨论，第五节作了总结。

二、NON-SEPARABLE TRANSFORM

将不可分离变换应用于二维N×N输入预测残差块X，如下所示：

输入的残差X首先被拉伸到长度为N2的向量，如下所示：

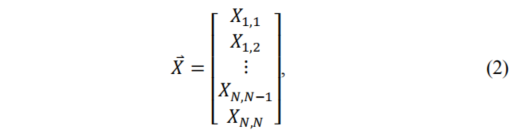
然后通过执行以下计算应用不可分离变换：

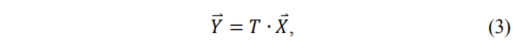
式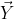表示应用不可分离变换后导出的变换系数向量，T是N2×N2变换矩阵。最后，将变换系数向量中的分量重新组织为N×N块，从而可以有效地应用后续基于块的熵编码。对系数向量的重新组织进行处理，使索引较小的系数与较小的扫描索引放在N×N系数块中。这样，先扫描较大幅度的系数，符合扫描顺序设计的原则。 

众所周知，不可分离变换通常比可分离变换更有效地探索二维方向纹理图案的像素间相关性。然而，对于实际的视频编解码器设计来说，不可分离的变换因为以下两个原因仍然不被考虑：1）计算复杂性的显著增加; 2）存储不可分变换矩阵的过大的存储器需求。

考虑使用矩阵乘法对N×N剩余块执行变换，可分变换的存储要求和运算计数分别为O（N2）和O（N3），而对于不可分变换，则分别为O（N4）和O（N4）。较大变换块大小的计算和存储器复杂度的急剧增加使得使用16×16或更大的块变换实际上是不可行的，尽管它们将产生高编码增益，特别是对于大分辨率视频内容（例如1080p和4k）。

三、 PROPOSED NON-SEPARABLE SECONDARY TRANSFORM

为了减少使用不可分离变换的复杂度以及保持其大部分编码增益，提出将不可分变换应用于二次变换。二次变换是主变换和量化过程之间的附加变换过程。在主变换不足以使残余样本去相关的情况下，对主变换系数进一步应用二次变换以进一步减少统计冗余。

A. Non-Separable Secondary Transform Process

为了应用所提出的不可分离二次变换（NSST），首先对N×N残差块X应用全尺寸可分离变换作为主变换，并导出变换系数块Y：

其中L和R分别表示左（垂直）和右（水平）变换矩阵，Y表示变换系数块， 

之后，系数块Y被拉伸成系数向量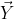，如下所示：

 应用不可分离变换：

式表示应用二次变换后导出的变换系数向量，T是×变换矩阵。最后，系数向量中的分量随后使用该块的扫描顺序（水平、垂直或对角线）重新组织为N×N块。此外，等式（4）也可以写成：

其是X的矢量表示，而B实际上是L和RT的克罗内克积（Kronecker product），即B=L⨂。通过组合（6）和（7），NSST的输出公式如下：，

 基本上，二次变换仅应用于低频分量，例如左上4×4或8×8，这意味着T是稀疏矩阵。应用不可分变换作为二次变换有两个好处：1）对于较大的变换系数块，可以采用较小的大小（如4×4）的不可分变换；2）对于不同的块大小，可以共享不可分变换。

B. Secondary Transform Selection and Signaling

对于4×4变换系数块，只使用4×4不可分离变换，这是基于离线训练得到的KLTs。对于8x8及更大的变换系数块，对低频8×8变换系数进行8×8不可分离变换。若要可视化不可分离二次变换基的方向性，请将（8）视为单个不可分离变换，

其中S=T·B是不可分变换矩阵。

在图1和图2中，分别示出了的可分离DCT-2和所提出的45°帧内预测方向不可分离变换S的基图像。很明显，变换S的基图像的方向性与相应的帧内预测方向一致，而DCT-2变换的基图像只适应水平和垂直方向。

在HEVC中，亮度分量共有35种帧内预测模式，包括平面模式、DC模式和33种方向预测模式。基于方向预测模式的对称性，本文采用了19×3的不可分离变换，其中19表示不同的帧内预测模式，包括平面（0）、DC（1）和前17个方向帧内预测模式2~18，3表示每个帧内预测模式的三个不可分离变换候选者。对于从19到34的帧内预测模式ipm，在应用二次变换之前，对其应用36-ipm模式对应的不可分离变换，并且对变换系数块进行转置。

为每个编码单元（CU）发送一个索引，即NSST索引，以指示在三个候选单元中应用了哪种二次转换。如果索引值被标记为0，则不应用二次变换。否则，选择帧内预测模式指定的三个不可分离的二次变换候选者中的一个，并且也向索引发送信号。

四、EXPERIMENTAL RESULTS

本文提出的不可分变换（NSST）是在HEVC参考软件HM 16.6[22]上实现的。由视频编码联合协作小组（JCT-VC）在[23]中规定的用于评估HEVC开发技术贡献的通用测试条件被用于执行模拟。在实验中，使用了一组28个视频序列，从416x240到4K的分辨率，作为测试序列。还包括四个带有计算机屏幕和自然内容和屏幕内容混合的人工序列。JVET推荐测试视频序列用于评估在联合勘探模型（JEM）基础上开发的技术方案[21]。常用的Bjøntegaard delta比特率（BDR）[24][25]用于评估编码增益。量化参数（QP）设置为22、27、32和37。测试了具有主10配置文件的全帧内（AI）和随机存取（RA）编码配置。在评估运行时差异时，使用Anchor与测试方法之间的比率，如.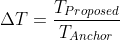

为了更好地了解应用不同大小NSST（4x4和8x8）的性能，对所提出方法的两个变体进行了测试。一种是在低频4×4变换系数区域仅应用4×4NSST。另一种测试方案是在4×4系数块上应用4×4NSST，在8×8及更大系数块大小的低频8×8变换系数区域上应用8×8NSST。

表1列出了编码性能和编码器/解码器运行时增加（ΔTEnc/ΔTDec）。对于AI和RA配置，建议的4x4 NSST实现了-3.5%和-3.1%的增益，编码器运行时间分别为331%和92%。当所提出的8x8不可分离二次变换用于8×8和更大的块大小时，对于AI和RA配置，编码增益分别为-6.0%和-4.6%，而编码器的运行时间分别为419%和99%。

从表1可以看出，所提出的NSST的编码增益明显取决于视频内容的纹理模式。对于具有丰富方向性纹理的视频内容，如图3所示的BasketballDrill，编码增益可达11.5%。图4还显示了使用AI配置编码BasketballDrill的PSNR速率曲线的比较。

五、CONCLUSIONS

本文提出了一种不可分离的二次变换，并在HEVC上实现。该方法对低频率变换系数进行小尺寸不可分变换，从而大大降低了对较大残差块尺寸应用不可分变换的计算成本。实验结果表明，与HEVC帧内编码相比，该方法可以获得高达12%的编码增益。

六、REFERENCES

[1] Draft ITU-T Recommendation and Final Draft International Standard of Joint Video Specification (ITU-T Rec.H.264jISO/IEC 14496-10 AVC), document JVT-G050, Joint Video Team (JVT) of ISO/IEC MPEG and ITU-T VCEG, Mar. 2003. 
[2] J. Bankoski, R. S. Bultje, A. Grange, Q. Gu, J. Han, J. Koleszar, D. Mukherjee, P. Wilkins, and Y. Xu, “Towards a next generation opensource video codec,” Proc. SPIE 8666, Visual Information Processing and Communication IV, Feb. 21, pp. 1-13, 2013. 
[3] G. J. Sullivan, J. Ohm, W. J. Han, and T. Wiegand, “Overview of the High Efficiency Video Coding (HEVC) standard,” IEEE Trans. Circuits and Syst. for Video Technol., vol. 22, no. 12, pp. 1649–1668, 2012. 
[4] J. Chen, Y. Chen, M. Karczewicz, X. Li, H. Liu, L. Zhang, X. Zhao, “Coding tools investigation for next generation video coding”, ITU-T SG16 Doc. COM16–C806, Feb. 2015. 
[5] X. Zhao, J. Chen, M. Karczewicz, L. Zhang, X. Li and W.-J. Chien, “Enhanced Multiple Transform for Video Coding,” to be published in Data Compression Conference, 2016. 
[6] X. Zhao, J. Chen, M. Karczewicz, “Mode-dependent non-separable secondary transform”, ITU-T SG16/Q6 Doc. COM16–C1044, Oct. 2015. 
[7] K. Karhunen and Kari, “Über lineare methoden in der wahrscheinlichkeitsrechnung,” Ann. Acad. Sci. Fennicae. Ser. A. I. Math.-Phys., no. 37, pp. 1–79, 1947. 
[8] M. Loève, Probability Theory, II (Graduate Texts in Mathematics, 4th ed.). Berlin, Germany: Springer-Verlag, 1978. 
[9] R. J. Clarke, “Relation between the Karhunen–Loève and cosine transforms,” Proc. Inst. Electr. Eng. F, vol. 128, no. 6, pp. 359–360, Nov. 1981.

[10] R. H. Bamberger and M. J. T. Smith, “A filter bank for the directional decomposition of images: Theory and design,” IEEE Trans. Signal Process., vol. 40, no. 4, pp. 882–893, Apr. 1992. 
[11] E. J. Candès and D. L. Donoho, “Ridgelets: A key to higher dimensional intermittency,” Phil. Trans. R. Soc. Lond. A, vol. 357, no. 1760, pp. 2495–2509, 1999. 
[12] J. L. Starck, E. J. Candes, and D. L. Donoho, “The curvelet transform for image denoising,” IEEE Trans. Image Process., vol. 11, no. 6, pp. 670–684, Jun. 2002. 
[13] M. N. Do and M. Vetterli, “The contourlet transform: An efficient directional multiresolution image representation,” IEEE Trans. Image Process., vol. 14, no. 12, pp. 2091–2106, Dec. 2005. 
[14] B. Zeng and J. Fu, “Directional discrete cosine transforms: A new framework for image coding,” IEEE Trans. Circuits Syst. Video Technol., vol. 18, no. 3, pp. 305–313, Mar. 2008. 
[15] Y. Ye and M. Karczewicz, “Improved H.264 intra coding based on bidirectional intra prediction, directional transform, and adaptive coefficient scanning,” in Proc. IEEE International Conference on Image Processing (ICIP), pp. 2116–2119, Oct. 2008. 
[16] X. Zhao, L. Zhang, S. Ma, and W. Gao, “Rate-distortion optimized transform for intra-frame coding,” in Proc. IEEE International Conference on Acoustics, Speech and Signal Processing, pp. 1414–1416, 2010. 
[17] X. Zhao, L. Zhang, S. Ma, and W. Gao, “Video coding with rate-distortion optimized transform,” IEEE Trans. Circuits Syst. Video Technol., vol 22, no. 1, pp. 138–151, 2012. 
[18] A. Arrufat, P. Philippe, and O. Déforges, “Non-separable mode dependent transforms for intra coding in HEVC,” in IEEE Proc. on Visual Communications and Image Processing, pp. 61–64, 2014. 
[19] S. Takamura and A. Shimizu, “On Intra Coding Using Mode Dependent 2D-KLT,” Picture Coding Symposium, pp. 137–140, 2013. 
[20] A. Saxena, and F. C. Fernandes. “On secondary transforms for prediction residual.” In Proc. IEEE International Conference on Image Processing, pp. 2489–2492, 2012. 
[21] JEM software, https://vceg.hhi.fraunhofer.de/svn/svn_HMJEMSoftware/ tags/HM-16.6-JEM-1.0/ 
[22] HEVC reference software, https://hevc.hhi.fraunhofer.de/svn/svn_HEVCSoftware/tags/HM-16.6/ 
[23] F. Bossen, “Common HM test conditions and software reference configurations,” Joint Collaborative Team on Video Coding (JCT-VC) of ITU-T SG16 WP3 and ISO/IEC JTC1/SC29/WG11, Doc. JCTVC-L1100, 12th Meeting., Geneva, CH, Jan. 2013. 
[24] G. Bjøntegaard, “Calculation of average PSNR differences between RDCurves,” ITU-T SG16/Q6, Doc. VCEG-M33, Austin, Apr. 2001. 
[25] G. Bjøntegaard, “Improvement of BD-PSNR model,” ITU-T SG16/Q6, Doc. VCEG-AI11, Berlin, Germany, Jul. 2008.