标题:剪格子
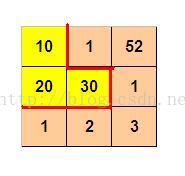
如图p1.jpg所示,3 x 3 的格子中填写了一些整数。
我们沿着图中的红色线剪开,得到两个部分,每个部分的数字和都是60。
本题的要求就是请你编程判定:对给定的m x n 的格子中的整数,是否可以分割为两个部分,使得这两个区域的数字和相等。
如果存在多种解答,请输出包含左上角格子的那个区域包含的格子的最小数目。
如果无法分割,则输出 0
程序输入输出格式要求:
程序先读入两个整数 m n 用空格分割 (m,n<10)
表示表格的宽度和高度
接下来是n行,每行m个正整数,用空格分开。每个整数不大于10000
程序输出:在所有解中,包含左上角的分割区可能包含的最小的格子数目。
例如:
用户输入:
3 3
10 1 52
20 30 1
1 2 3
则程序输出:
3
再例如:
用户输入:
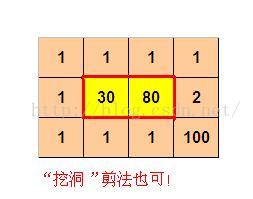
4 3
1 1 1 1
1 30 80 2
1 1 1 100
则程序输出:
10
资源约定:
峰值内存消耗 < 64M
如图p1.jpg所示,3 x 3 的格子中填写了一些整数。
我们沿着图中的红色线剪开,得到两个部分,每个部分的数字和都是60。
本题的要求就是请你编程判定:对给定的m x n 的格子中的整数,是否可以分割为两个部分,使得这两个区域的数字和相等。
如果存在多种解答,请输出包含左上角格子的那个区域包含的格子的最小数目。
如果无法分割,则输出 0
程序输入输出格式要求:
程序先读入两个整数 m n 用空格分割 (m,n<10)
表示表格的宽度和高度
接下来是n行,每行m个正整数,用空格分开。每个整数不大于10000
程序输出:在所有解中,包含左上角的分割区可能包含的最小的格子数目。
例如:
用户输入:
3 3
10 1 52
20 30 1
1 2 3
则程序输出:
3
再例如:
用户输入:
4 3
1 1 1 1
1 30 80 2
1 1 1 100
则程序输出:
10


资源约定:
峰值内存消耗 < 64M
CPU消耗 < 5000ms
思路:用搜索。要求将这个矩阵分割成两块相等的区域。只要从第一个格子出发,像走迷宫一样,遍历没有走过的路,如果等于sun/2,说明算是一种分割方法,就拿这个格子数和上一次的方法的格子数比较,如果这个比较小,就替换。
#include<iostream>
#include<cstring>
using namespace std;
int a[110][110];
int b[110][110];
int m,n,sum=0;
int MIN=0,NUM=100000000;
void dfs(int x,int y,int s,int N){
if(s>sum)
return;
if(s==sum){
if(N<NUM)
NUM=N;
return;
}
//四个方向逆时针递归
if(x+1<=m&&b[x+1][y]==0)
{
b[x+1][y]=1;
dfs(x+1,y,s+a[x+1][y],N+1);
b[x+1][y]=0;
}
if(y+1<=n&&b[x][y+1]==0)
{
b[x][y+1]=1;
dfs(x,y+1,s+a[x][y+1],N+1);
b[x][y+1]=0;
}
if(x-1>0&&b[x-1][y]==0)
{
b[x-1][y]=1;
dfs(x-1,y,s+a[x-1][y],N+1);
b[x-1][y]=0;
}
if(y-1>0&&b[x][y-1]==0)
{
b[x][y-1]=1;
dfs(x,y-1,s+a[x][y-1],N+1);
b[x][y-1]=0;
}
}
int main(){
memset(a,0,sizeof(a));
memset(b,0,sizeof(b));
cin>>n>>m;
int i,j;
for(i=1;i<=m;i++)
for(j=1;j<=n;j++)
{
cin>>a[i][j];
sum+=a[i][j];
}
sum/=2;
dfs(1,1,a[1][1],1);
cout<<NUM<<endl;
return 0;
} 




 本文介绍了一个编程问题,即判断一个给定的mxn矩阵中的整数是否可以被分割成两个和相等的部分,并通过搜索算法寻找包含左上角单元格的最小分割区域。
本文介绍了一个编程问题,即判断一个给定的mxn矩阵中的整数是否可以被分割成两个和相等的部分,并通过搜索算法寻找包含左上角单元格的最小分割区域。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








