DP 类型题一
- 一、数字三角形模型:只能朝右或下走
- 二、最长上升子序列模型
- 三、背包模型
- 1、 AcWing 532. 货币系统 :极大独立集
- 2、单调队列优化多重背包 O(NM)
- 3、AcWing 7. 混合背包问题
- 4、AcWing 8. 二维费用的背包问题
- 5、AcWing 1020. 潜水员:dp[i][j] 下标表示不小于
- 6、AcWing 1013. 机器分配 :求具体方案
- 7、AcWing 12. 背包问题求具体方案 :求字典序最小的具体方案
- 8、AcWing 11. 背包问题求方案数 :求最优解的方案数
- 9、AcWing 487. 金明的预算方案 :二进制枚举构造分组背包的决策
- 10、AcWing 10. 有依赖的背包问题 :树形套分组
- 11、AcWing 734. 能量石 :贪心+变种01
一、数字三角形模型:只能朝右或下走
1、AcWing 1018. 最低通行费:只走一次
//只从左边或者上面过来
#include <bits/stdc++.h>
using namespace std;
#define getlen(array) {return (sizeof(array) / sizeof(array[0]));}
#define ll long long
#define ull unsigned long long
#define PII pair<int, int>
#define PLL pair<ll, ll>
#define MEM(x, y) memset(x, y, sizeof x)
#define rin int n; scanf("%d", &n)
#define rln ll n; scanf("%lld", &n)
#define rim int m; scanf("%d", &m)
#define rit int t; scanf("%d", &t)
#define ria int a; scanf("%d", &a)
#define sc scanf
#define pr printf
const int INF = 0x3f3f3f3f;
const int N = 110;
int dx[] = {-1, 1, 0, 0}, dy[] = {0, 0, -1, 1};
int nums[N][N];
int main() {
//freopen("D:\\in.txt", "r", stdin);
rin;
MEM(nums, INF); //需要把临边改为无穷大,否则诸如nums[1][2]会一直等于本身
nums[0][1] = 0; //同理不让第一个点硬加上INF
for (int i = 1; i <= n; ++ i) {
for (int j = 1; j <= n; ++ j) {
cin >> nums[i][j];
nums[i][j] += min(nums[i - 1][j], nums[i][j - 1]);
}
}
cout << nums[n][n];
return 0;
}
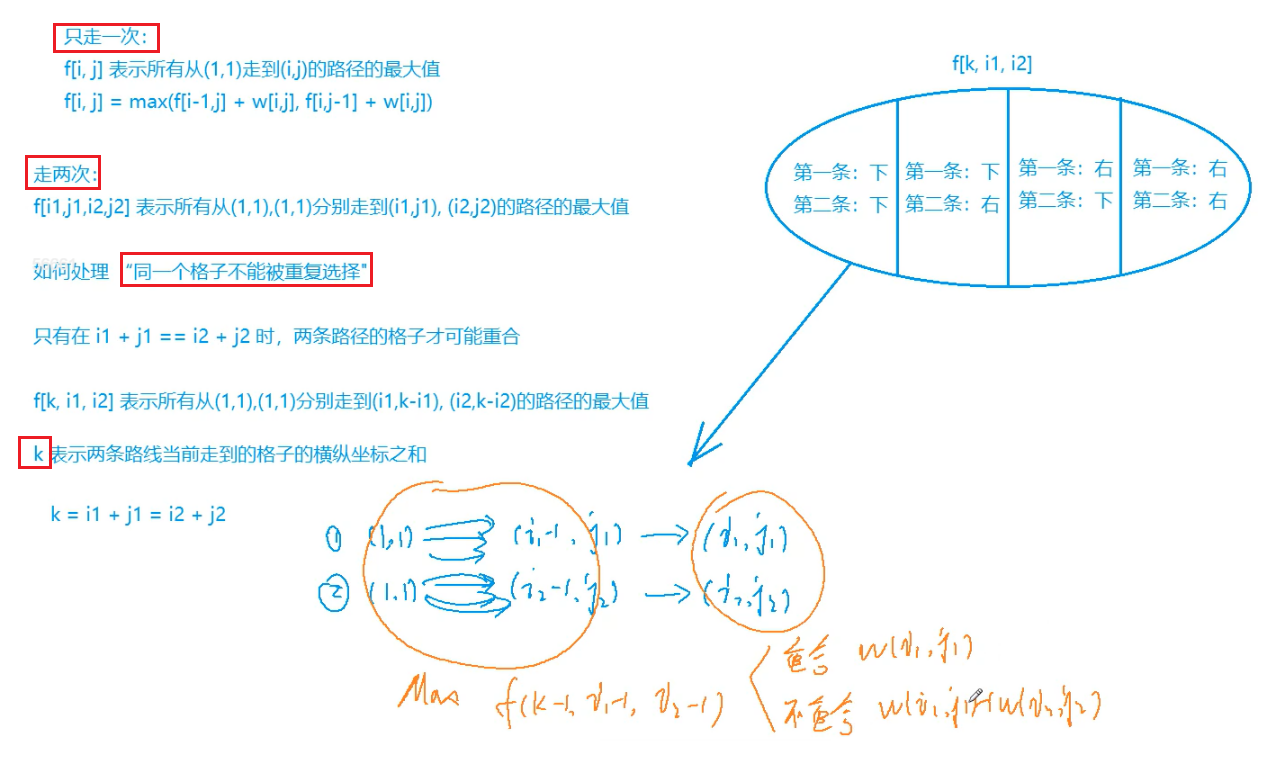
2、AcWing 1027. 方格取数:走两次,只拿一次,且可重复
/*
k - 当前位置横纵坐标之和
i1 - 第一条路线走到的横坐标
i2 - 第二条路线走到的横坐标
*/
#include<bits/stdc++.h>
using namespace std;
const int N = 20;
int nums[N][N];
int dp[2 * N][N][N];
int main() {
int n, r, c, num;
cin >> n;
while (cin >> r >> c >> num, r | c | num) {
nums[r][c] = num;
}
for (int k = 2; k <= 2 * n; ++ k) {
for (int i1 = 1; i1 <= n; ++ i1) {
for (int i2 = 1; i2 <= n; ++ i2) {
int j1 = k - i1, j2 = k - i2;
if (j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n) { //位置的合法性
int t = nums[i1][j1];
if (i1 != i2 && j1 != j2) t += nums[i2][j2]; //两个点若是同一个,不可以重复计算
int & v = dp[k][i1][i2];
v = max(v, dp[k - 1][i1 - 1][i2 - 1] + t);
v = max(v, dp[k - 1][i1 - 1][i2] + t);
v = max(v, dp[k - 1][i1][i2 - 1] + t);
v = max(v, dp[k - 1][i1][i2] + t);
}
}
}
}
cout << dp[2 * n][n][n];
return 0;
}
3、AcWing 275. 传纸条:走两次,只拿一次,且不可重复
【解法一】
其实这一题和上一题的取方格数可以是完全一样的代码 ac 掉,在下面的传送门有详细说明。
证明最终结果一定可以不交叉又是最大值
【解法二】
在重复点处进行特判,如下代码注释:
#include<bits/stdc++.h>
using namespace std;
const int N = 60;
int nums[N][N];
int dp[2 * N][N][N];
int main() {
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; ++ i) {
for (int j = 1; j <= m; ++ j) {
cin >> nums[i][j];
}
}
for (int k = 2; k <= n + m; ++ k) {
for (int i1 = 1; i1 <= n; ++ i1) {
for (int i2 = 1; i2 <= n; ++ i2) {
int j1 = k - i1, j2 = k - i2;
if (j1 >= 1 && j1 <= m && j2 >= 1 && j2 <= m) {
//除了起点和终点外的点不可以重复走,若重复了,说明该方案不可行,设为无穷小
if (i1 == i2 && j1 == j2 && k != 2 && k != n + m) {
dp[k][i1][i2] = -0x3f3f3f3f;
continue;
}
int t = nums[i1][j1];
if (i1 != i2 && j1 != j2) t += nums[i2][j2];
int &v = dp[k][i1][i2];
v = max(v, dp[k - 1][i1 - 1][i2 - 1] + t);
v = max(v, dp[k - 1][i1 - 1][i2] + t);
v = max(v, dp[k - 1][i1][i2 - 1] + t);
v = max(v, dp[k - 1][i1][i2] + t);
}
}
}
}
cout << dp[n + m][n][n];
return 0;
}
二、最长上升子序列模型
1、AcWing 1014. 登山:既上山又下山
原题链接:https://www.acwing.com/problem/content/1016/
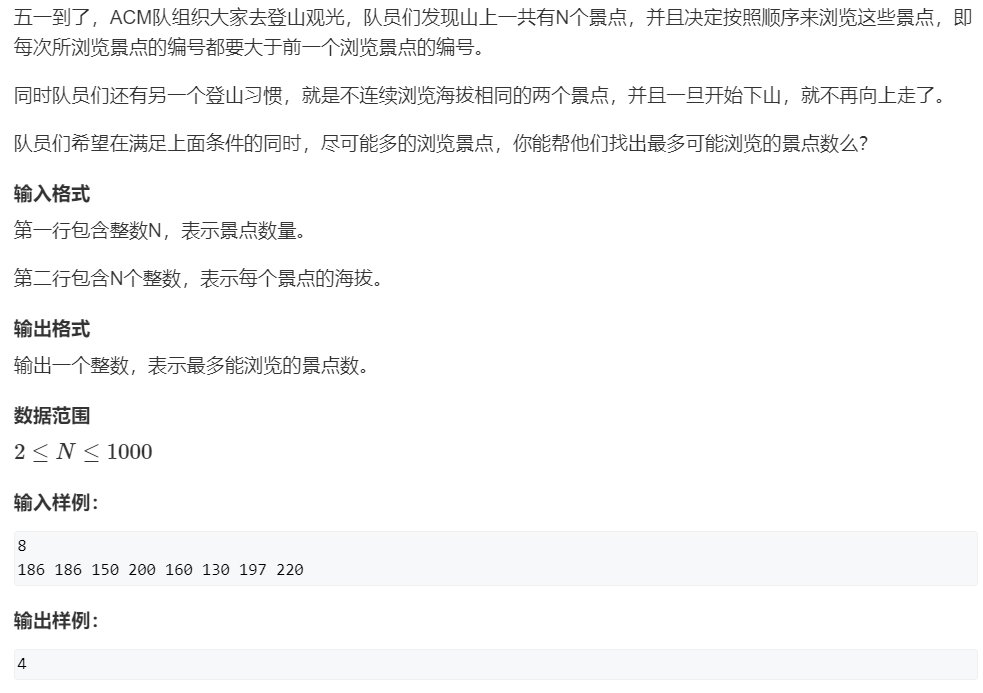
/*
旅程其实是包括上山和下山的,下山也是可以看景点的……
所以就是求从山脚到位置 i 和 i 到山脚过程中,满足游玩景点的编号符合从小到大即可
*/
#include <bits/stdc++.h>
using namespace std;
#define getlen(array) {return (sizeof(array) / sizeof(array[0]));}
#define ll long long
#define ull unsigned long long
#define PII pair<int, int>
#define PLL pair<ll, ll>
#define MEM(x, y) memset(x, y, sizeof x)
#define rin int n; scanf("%d", &n)
#define rln ll n; scanf("%lld", &n)
#define rim int m; scanf("%d", &m)
#define rit int t; scanf("%d", &t)
#define ria int a; scanf("%d", &a)
#define sc scanf
#define pr printf
const int INF = 0x3f3f3f3f;
const int N = 1010;
int dx[] = {-1, 1, 0, 0}, dy[] = {0, 0, -1, 1};
int up[N], down[N], nums[N];
int main() {
//freopen("D:\\in.txt", "r", stdin);
int n;
cin >> n;
nums[0] = nums[n + 1] = -INF;
for (int i = 1; i <= n; ++ i) cin >> nums[i];
int ans = 0;
//up[i]:从 1 走到 i 的最长上升子序列
for (int i = 1; i <= n; ++ i) {
for (int j = 0; j < i; ++ j) {
if (nums[j] < nums[i]) up[i] = max(up[i], up[j] + 1);
}
}
//down[i]:从 n 走到 i 的最长上升子序列 == 从 i 走到 n 的最长下降子序列
for (int i = n; i >= 1; -- i) {
for (int j = n + 1; j > i; -- j) {
if (nums[i] > nums[j]) down[i] = max(down[i], down[j] + 1);
}
}
for (int i = 1; i <= n; ++ i) ans = max(ans, up[i] + down[i] - 1);
cout << ans;
return 0;
}
2、AcWing 1012. 友好城市:线性互不交叉
原题链接:https://www.acwing.com/problem/content/1014/
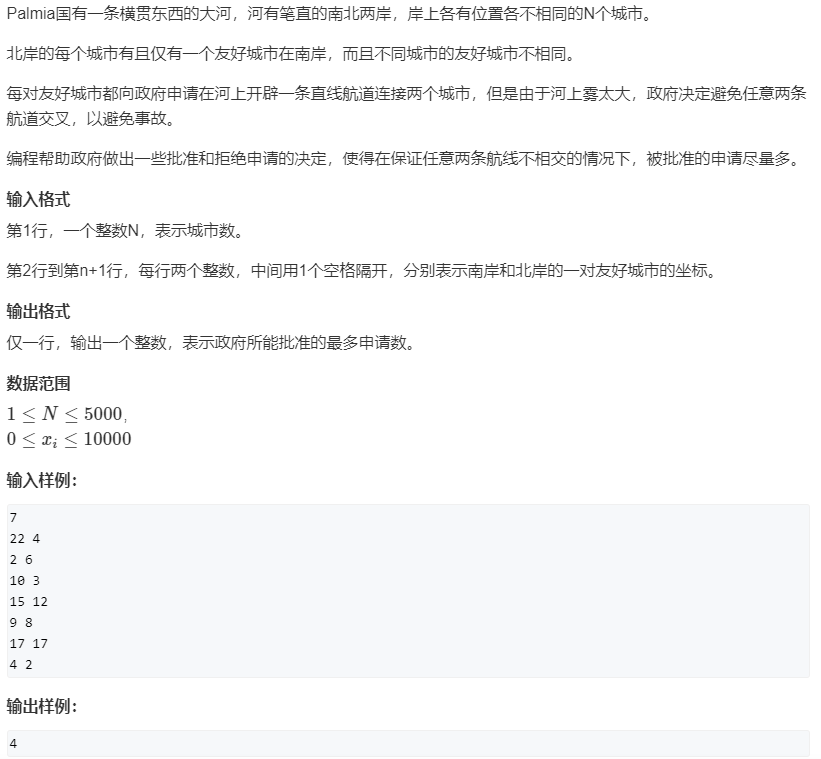
/*
在按照如下规则排序后,最大不交叉数目就是最长上升子序列的元素数目
因为要想不交叉,那么第 i + 1 个北岸城市在南岸的友好城市的位置必须比第 i 个的大。
抽象出来就是最长上升子序列,只不过多了对北岸城市正序排序的操作。
*/
#include<bits/stdc++.h>
using namespace std;
const int N = 5010;
struct node{
int up, down; //分别表示北岸和南岸的位置
}arr[N];
//按照北岸的位置从左到右排序
bool cmp(node a, node b) {
return a.up < b.up;
}
int dp[N];
int main() {
int n;
cin >> n;
for (int i = 1; i <= n; ++ i) {
int a, b;
cin >> a >> b;
arr[i] = {a, b};
}
sort(arr + 1, arr + n + 1, cmp);
int ans = 0;
for (int i = 1; i <= n; ++ i) {
for (int j = 0; j < i; ++ j) {
if (arr[j].down < arr[i].down) dp[i] = max(dp[i], dp[j] + 1);
}
ans = max(ans, dp[i]);
}
cout << ans;
return 0;
}
3、AcWing 1016. 最大上升子序列和
原题链接:https://www.acwing.com/problem/content/1018/
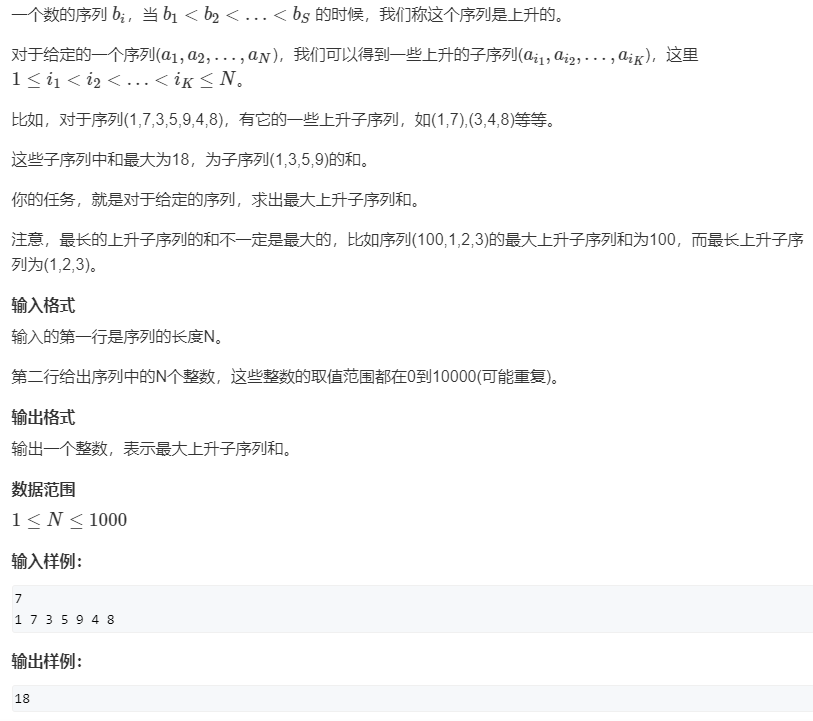
/*
模式和最长上升子序列是一样的,不同在于,每一次在前面找到可以接的位置
时,是判断数值而不是个数。
*/
#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int nums[N], dp[N];
int main() {
int n;
cin >> n;
for (int i = 1; i <= n; ++ i) cin >> nums[i];
int ans = 0;
for (int i = 1; i <= n; ++ i) {
dp[i] = nums[i];
for (int j = 1; j < i; ++ j) {
if (nums[j] < nums[i]) dp[i] = max(dp[i], dp[j] + nums[i]);
}
ans = max(ans, dp[i]);
}
cout << ans;
return 0;
}
4、AcWing 1010. 拦截导弹:最长上升子序列 == 最少用多少个非上升子序列才能填满整个序列(反之亦然)
原题链接:https://www.acwing.com/problem/content/1012/
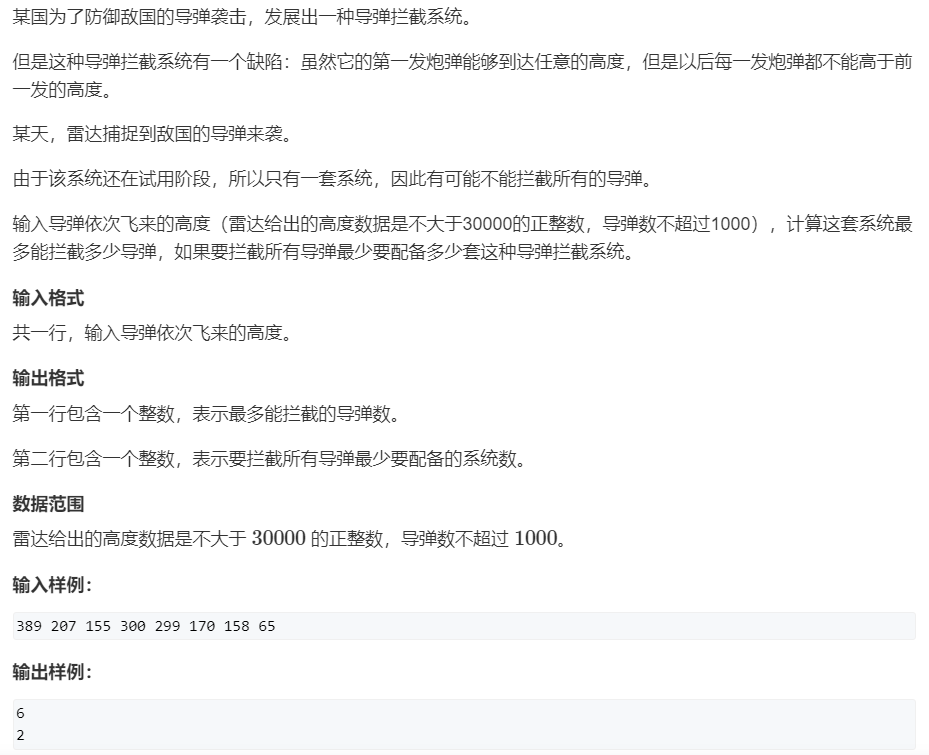
思路

到了这里,我们可以惊人地发现,似乎和最长上升子序列的贪心求法有异曲同工之妙。
而且,明明是要求至少需要多少个非上升子序列可以把整个序列填满,答案却恰恰是最长上升子序列的长度。
想来也不乏道理。初略来讲,对于一个最长上升子序列来说,是整个序列所有能构成上升序列的最长长度,假设该序列为 a b c d e,必然有前者严格小于后者的规则。
那么要想用非上升序列填满整个序列,显然,a、b、c、d、e 不可能处于同一个非上升(前者严格大于等于后者)子序列,故而至少需要 5 个非上升子序列,对应本题也就是至少需要 5 个拦截系统。
同理,最长下降子序列也对应着最少需要多少个非下降子序列才能填满。
当然,这也意味着,如若转换问题,那么题目的数据范围可达到 10 ^ 6,因为贪心解法为 nlogn (需要用到二分),具体可移步 第二点的 AcWing 896. 最长上升子序列 II(n = 10^5 nlogn的做法)。
【解法一】 最长上升子序列 == 最少用多少个非上升子序列才能填满整个序列 O (n ^ 2)
#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
const int INF = 0x3f3f3f3f;
priority_queue<int> q;
int nums[N], down[N], up[N];
int main() {
int a, n = 0;
while (scanf("%d", &a) != EOF) nums[++ n] = a;
//裸求最长非上升子序列
int maxx = 0;
nums[0] = INF;
for (int i = 1; i <= n; ++ i) {
for (int j = 0; j < i; ++ j) {
if (nums[j] >= nums[i]) down[i] = max(down[i], down[j] + 1);
}
maxx = max(maxx, down[i]);
}
//裸求最长上升子序列
int minn = -INF;
nums[0] = -INF;
for (int i = 1; i <= n; ++ i) {
for (int j = 0; j < i; ++ j) {
if (nums[j] < nums[i]) up[i] = max(up[i], up[j] + 1);
}
minn = max(minn, up[i]);
}
cout << maxx << endl << minn;
return 0;
}
【解法二】常规解法 — 大根堆
#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
priority_queue<int> q;
int nums[N], dp[N];
int main() {
int a, n = 0;
//裸求最长非上升子序列
int maxx = 0;
nums[0] = 0x3f3f3f3f;
for (int i = 1; i <= n; ++ i) {
for (int j = 0; j < i; ++ j) {
if (nums[j] >= nums[i]) dp[i] = max(dp[i], dp[j] + 1);
}
maxx = max(maxx, dp[i]);
}
//用大根堆贪心求最少个数
while (scanf("%d", &a) != EOF) {
nums[++ n] = a;
if (q.empty() || q.top() < a) q.push(a);
else {
stack<int> s;
while (!q.empty() && q.top() >= a) {
s.push(q.top());
q.pop();
}
s.pop();
while (!s.empty()) {
q.push(s.top());
s.pop();
}
q.push(a);
}
}
cout << maxx << endl << q.size();
return 0;
}
5、AcWing 187. 导弹防御系统 :最少上升+下降子序列覆盖完整序列
原题链接:https://www.acwing.com/problem/content/description/189/

思路
首先,设置两个集合,集合 A 放置所有上升子序列,集合 B 放置所有下降子序列。
可以有一个大胆的想法,每一枚子弹要么放在集合A,要么B,换句话说,每枚子弹只有两种可能,当选择好阵营后,根据本篇博客的上一题可以在O(n)复杂度下贪心找到最优放置的位置(甚至可以用二分优化成 logn ),整套下来 n * 2 ^ n 可以解决。
看一眼数据范围,n 小于等于 50,乍以为会跑炸,但其实不会。
显然不能用二进制枚举去遍历每一种方案,但是可以从小到大枚举最少子序列数目。
假如最终答案为 ans,那么显然在 dfs 中复杂度为 ans * (2 ^ ans)。
下面证明 ans <= n / 2 上取整。
假如数据很极端:
① 导弹高度从大到小或者从小到大
这种在二进制枚举确实很死亡,但是会在上诉解法中 ans == 1的时候就跑出来了,不会跑炸。
② 相同的高度很多,比如 1 1 1 1 1 1 1 1 1 0
这种如果真的连续几十个 1 确实会把dfs跑炸,但是题目输入明确表示不会有相同的高度:“ 第二行包含 n 个不同的整数,表示每个导弹的高度。 ”
③ 上升下降交叉着来,尽量不让连成较长的子序列
即便数据很诡异,像 60 70 50 65 58 这样尽量不让连成长一点的子序列,但是最差也能互相两两配对,换句话说,ans 最多也只需要 n / 2上取整。那么显然 2 ^ 25 在 3 s内是可以跑完的,或者讲究的话把 O(n)部分优化成 logn 也可以,但是这道题ans 应该很难接近 n / 2。
#include<bits/stdc++.h>
using namespace std;
const int N = 60;
const int INF = 0x3f3f3f3f;
int n;
//up表示上升子序列集合,down表示下降子序列集合
int nums[N], up[N], down[N];
//sum-总的序列数 idx-当前安排到nums里的第几颗导弹
//u-up里面现在有几个子序列
//d-down里面现在有几个子序列
bool dfs(int sum, int idx, int u, int d) {
if (u + d > sum) return false; //不合法
if (idx > n) return true; //找到解了
//将当前导弹放入上升子序列集里
bool flag = true; //判断是不是现有的容纳不下nums[idx]
for (int i = 1; i <= u; ++ i) {
if (up[i] < nums[idx]) {
int temp = up[i]; //储存,方便恢复现场
up[i] = nums[idx]; //将当前导弹加入到该上升子序列后面
flag = false; //表示不需要新开一个子序列
if(dfs(sum, idx + 1, u, d)) return true; //递归查询该方案是否可行
up[i] = temp; //不可行则恢复现场,尝试其他可能
break;
}
}
//在up里面新开一个子序列
if (flag) {
up[u + 1] = nums[idx];
if(dfs(sum, idx + 1, u + 1, d)) return true;
//这里不需要重置数据,因为回归当层递归时,u还是u,不是u+1
}
//将当前导弹放入下降子序列集里
flag = true;
for (int i = 1; i <= d; ++ i) {
if (down[i] > nums[idx]) {
int temp = down[i];
down[i] = nums[idx];
flag = false;
if (dfs(sum, idx + 1, u, d)) return true;
down[i] = temp;
break;
}
}
if (flag) {
down[d + 1] = nums[idx];
return dfs(sum, idx + 1, u, d + 1);
}
return false;
}
int main() {
while (cin >> n, n) {
for (int i = 1; i <= n; ++ i) cin >> nums[i];
int ans = 1; //从小到大枚举最小所需子序列数
while (!dfs(ans, 1, 0, 0)) ++ ans;
cout << ans << endl;
}
return 0;
}
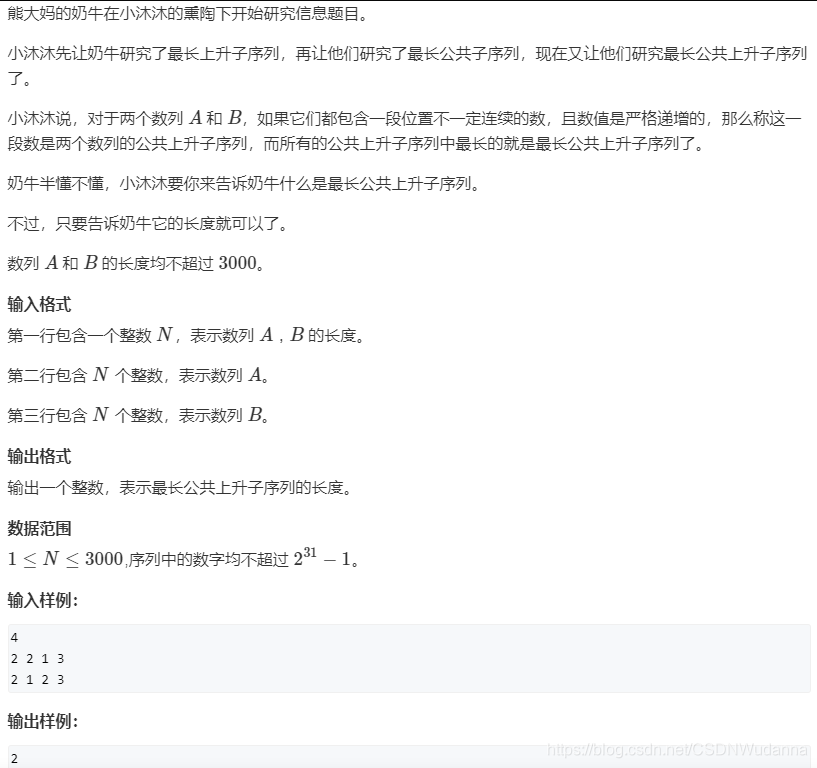
6、AcWing 272. 最长公共上升子序列
原题链接:https://www.acwing.com/problem/content/description/274/
思路
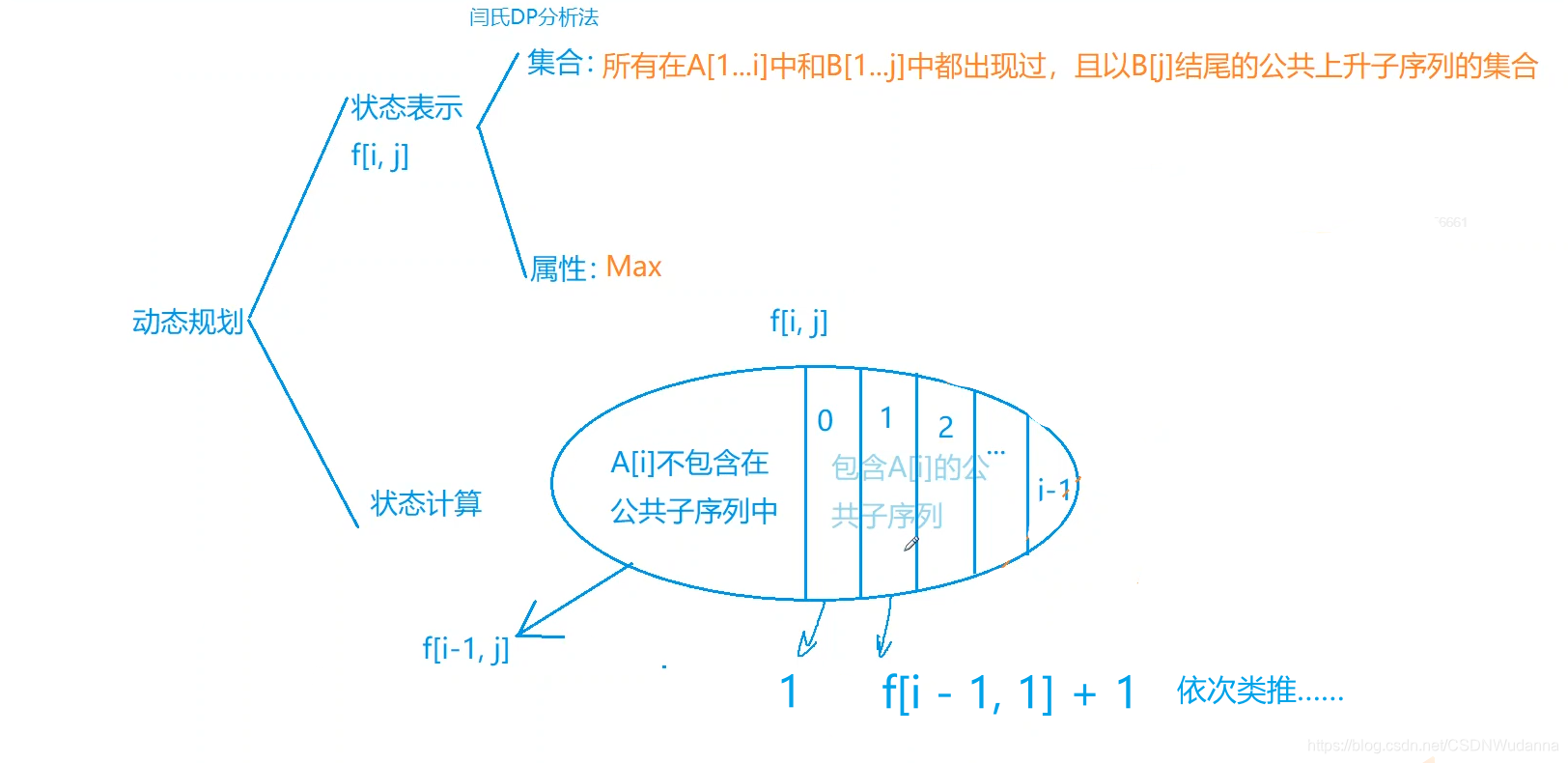
【解法一】 暴力 O(n ^ 3),超时,方便理解
#include<bits/stdc++.h>
using namespace std;
const int N = 3010;
int a[N], b[N], dp[N][N];
int main() {
int n;
cin >> n;
for (int i = 1; i <= n; ++ i) cin >> a[i];
for (int i = 1; i <= n; ++ i) cin >> b[i];
int ans = 0;
//枚举a序列
for (int i = 1; i <= n; ++ i) {
//枚举b序列
for (int j = 1; j <= n; ++ j) {
dp[i][j] = dp[i - 1][j]; //不含a[i]
if (a[i] == b[j]) {
dp[i][j] = max(dp[i][j], 1);
//找到前面符合要求的序列末尾
for (int k = 1; k < j; ++ k) {
if (b[k] < b[j]) dp[i][j] = max(dp[i][j], dp[i - 1][k] + 1);
}
}
ans = max(ans, dp[i][j]);
}
}
cout << ans;
return 0;
}
【解法二】优化成二维 O(n ^ 2)
每一次从头查找合适的上升子序列末尾的时候,其实只要保存并维护最大值即可,并不需要每一次都重复从头找到 j 。
#include<bits/stdc++.h>
using namespace std;
const int N = 3010;
int a[N], b[N], dp[N][N];
int main() {
int n;
cin >> n;
for (int i = 1; i <= n; ++ i) cin >> a[i];
for (int i = 1; i <= n; ++ i) cin >> b[i];
int ans = 0;
for (int i = 1; i <= n; ++ i) {
int maxx = 0; //b[1 ~ j] 中,能让a[i]接在后面构成上升子序列的最大序列长度
for (int j = 1; j <= n; ++ j) {
dp[i][j] = dp[i - 1][j]; //不含a[i]
if (a[i] == b[j]) dp[i][j] = max(dp[i][j], maxx + 1);
//只有b[j] < a[i],才有必要判断是否更新maxx
if (b[j] < a[i]) maxx = max(maxx, dp[i - 1][j]);
ans = max(ans, dp[i][j]);
}
}
cout << ans;
return 0;
}
三、背包模型
1、 AcWing 532. 货币系统 :极大独立集
原题链接:https://www.acwing.com/problem/content/534/


思路
简单来说就是一个完全背包,下面给出学习过程:
对于第一个样例 3、19、10、6 我们可以发现 6 和 19 没必要存在,因为可以被 3 和 10 表示出来,6 = 2 * 3 + 0 * 10,19 = 3 * 3 + 1 * 10。
我们可以先对 3、19、10、6 排序,得到 3、6、10、19,首先第 i 个数不可能被 i 之后的数表示出来,所以我们只需要考虑第 i 个数能不能被第 1 ~ i - 1 个数至少有一种方案表示出来,如果能,那么第 i 个数没有存在的必要,如果不能,那么这个数需要存在。
但思考到这里,我们会不由得想到,为什么不能就一定需要存在呢?就不能取原数组以外的数吗?
我们设原数组为 a ,更新后的数组为 b,假设 bi 存在于 b 而不存在于 a 中,但是根据题目要求 a 和 b 能表达的数范围是一致的,所以 a 中存在两个数及以上能恰好等于 bi,设为 bi = ax + ay + ……。同样的,又因为 a 和 b 能表达的数范围是一致的,所以 b 中能表示出 ax、ay、……,假设 ax = bx1 + bx2 + ……,ay = by1 + by
2 + ……,……。换而言之 bi = ax + ay + ……中的ax、ay等数能被 b 数组中的数等价替换掉,由此可以发现 bi = (bx1 + bx2 + ……)+(by1 + by2 + ……)+ ……。
既然 bi 能被 b 数组其他数表示,那本身是不必存在的,这对于题目中对 b 数组要求的 m 尽可能小矛盾,所以 b 数组必然是对 a 数组的精简。
故而我们可以先对 a 数组正序排序,再把题目抽象成完全背包问题,dp [ i - 1] [ a [ i ] ] 表示前 i - 1 个数能否至少存在一种方案凑出 a [ i ] 来。
#include<bits/stdc++.h>
using namespace std;
const int N = 110, M = 25010;
int a[N], dp[N][M]; //表示在前 i 种货币中,是否至少有一种方案恰好能凑成 j
int main() {
int t;
cin >> t;
while (t --) {
int n;
cin >> n;
for (int i = 1; i <= n; ++ i) cin >> a[i];
sort (a + 1, a + n + 1);
memset(dp, 0, sizeof dp);
int ans = 0;
for (int i = 1; i <= n; ++ i) {
if (!dp[i - 1][a[i]]) ++ ans;
for (int j = 1; j < M; ++ j) {
dp[i][j] = dp[i - 1][j];
//防止数据溢出,能判断是否大于0即可,不求具体方案数
if (j > a[i]) dp[i][j] |= dp[i][j - a[i]];
else if (j == a[i]) dp[i][j] |= 1;
}
}
cout << ans << endl;
}
return 0;
}
2、单调队列优化多重背包 O(NM)
AcWing 6. 多重背包问题 III
原题链接:https://www.acwing.com/problem/content/description/6/

/*
截至2021.07.30 做过最难受的DP
具体移步大佬的介绍:https://www.acwing.com/solution/content/6500/
① 以余数区分第 i 种物品能产生的搭配方案
② 用滑动窗口维护前s种选择,需要考虑:
Ⅰ 队头会不会滑出窗口
Ⅱ 队尾拖后腿就弹出
*/
#include<bits/stdc++.h>
using namespace std;
const int N = 20010;
//f[a] 代表 f[i][a]
//g[a] 代表 f[i - 1][a]
//q为数组模拟队列,维护f[i-1][j]中j的前s个,即:j-v、j-2v、……、j-sv
int f[N], g[N], q[N];
int main () {
int n, m;
cin >> n >> m;
//枚举第 i 个物品
for (int i = 1; i <= n; ++ i) {
int v, w, s;
cin >> v >> w >> s;
memcpy(g, f, sizeof f); //滚动数组保存数据
//枚举余数
for (int j = 0; j < v; ++ j) {
int hh = 0, tt = -1; //设置队列头尾指针(余数j不同保证了不会重复)
//枚举体积
for (int k = j; k <= m; k += v) {
// if (队列非空 && 队头 < k能接受的最小体积(即:队头滑出了窗口)) 弹出队头;
if (hh <= tt && q[hh] < k - s * v) ++ hh;
// if (队列非空) f[k] = max(不变, 前i-1种物品用q[hh]体积获得的最大价值+第i种物品用k-q[hh]体积获得的价值)
if (hh <= tt) f[k] = max(f[k], g[q[hh]] + (k - q[hh]) / v * w);
// while (队列非空 && 前i-1种物品中,体积为队尾的方案得到的价值 < 体积为k的方案得到的价值) 弹出队尾
while (hh <= tt && g[q[tt]] + (k - q[tt]) / v * w < g[k]) -- tt;
// 或者也可以把w提取出来,写成:while (hh <= tt && g[q[tt]] - q[tt] / v * w < g[k] - k / v * w) -- tt;
q[++ tt] = k;
}
}
}
cout << f[m];
return 0;
}
3、AcWing 7. 混合背包问题
原题链接:https://www.acwing.com/problem/content/7/


【朴素版 :二进制,没有优化空间】
/*
其实可以把 01 和完全分别看成多重里面的 1 和 m / v
剩余的和多重背包的二进制优化一样
*/
#include<iostream>
using namespace std;
const int N = 1010, M = 10010;
int v[M], w[M];
int dp[M][N];
int cnt = 1;
int main() {
int n, m;
cin >> n >> m;
for (int i = 0; i < n; ++ i) {
int vv, ww, ss;
cin >> vv >> ww >> ss;
//特判一下ss
if (ss == -1) ss = 1;
else if (ss == 0) ss = m / vv;
int num = 1;
while (num <= ss) {
v[cnt] = num * vv;
w[cnt] = num * ww;
++ cnt;
ss -= num;
num *= 2;
}
if (ss > 0) {
v[cnt] = ss * vv;
w[cnt] = ss * ww;
++ cnt;
}
}
//最后01一下,两种决策:取和不取
for (int i = 1; i < cnt; ++ i) {
for (int j = 1; j <= m; ++ j) {
dp[i][j] = dp[i - 1][j];
//无语 这里把v和w写反了一直debug
if (v[i] <= j) dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);
}
}
cout << dp[cnt - 1][m]; //糗 这里写成dp[n][m]了
return 0;
}
【改进版:优化空间 + 简洁写法】
/*
一开始想岔了,先循环了j再循环k,这导致了原先的第一维交叉转移状态。
因为在二进制优化的时候,其实每一个k都代表了在dp[i][j]中新生成了一个i。
如果先循环j会导致出现诸如dp[1][10]和dp[3][10]在同期转移,这是不合法的。
应该是先确定第一维再确定第二维,不能因为优化了空间,就默认当前的进程是需要的进程。
*/
#include<iostream>
using namespace std;
const int N = 1010;
long long dp[N];
int main() {
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; ++ i) {
int v, w, s;
cin >> v >> w >> s;
if (s == 0) s = m / v;
else if (s == -1) s = 1;
for (int k = 1; k <= s; k *= 2) {
s -= k;
int vv = k * v, ww = k * w;
for (int j = m; j >= vv; -- j)
dp[j] = max(dp[j], dp[j - vv] + ww);
}
if (s) {
int vv = s * v, ww = s * w;
for (int j = m; j >= vv; -- j)
dp[j] = max(dp[j], dp[j - vv] + ww);
}
}
cout << dp[m];
return 0;
}
4、AcWing 8. 二维费用的背包问题
原题链接:https://www.acwing.com/problem/content/8/

#include<iostream>
using namespace std;
const int N = 1010, M = 110;
//dp[i][j][k]表示:在前 i 件物品中,拿体积不超过j、总量不超过k的最大价值
int dp[N][M][M];
int main() {
int n, v, m;
cin >> n >> v >> m;
//枚举第几件物品
for (int i = 1; i <= n; ++ i) {
int vv, mm, ww;
cin >> vv >> mm >> ww;
//枚举体积
for (int j = 1; j <= v; ++ j) {
//枚举重量
for (int k = 1; k <= m; ++ k) {
int &x = dp[i][j][k];
x = dp[i - 1][j][k]; //不拿第i件物品
//拿第i件物品
if (vv <= j && mm <= k) x = max(x, dp[i - 1][j - vv][k - mm] + ww);
}
}
}
cout << dp[n][v][m];
return 0;
}
5、AcWing 1020. 潜水员:dp[i][j] 下标表示不小于
原题链接:https://www.acwing.com/problem/content/1022/

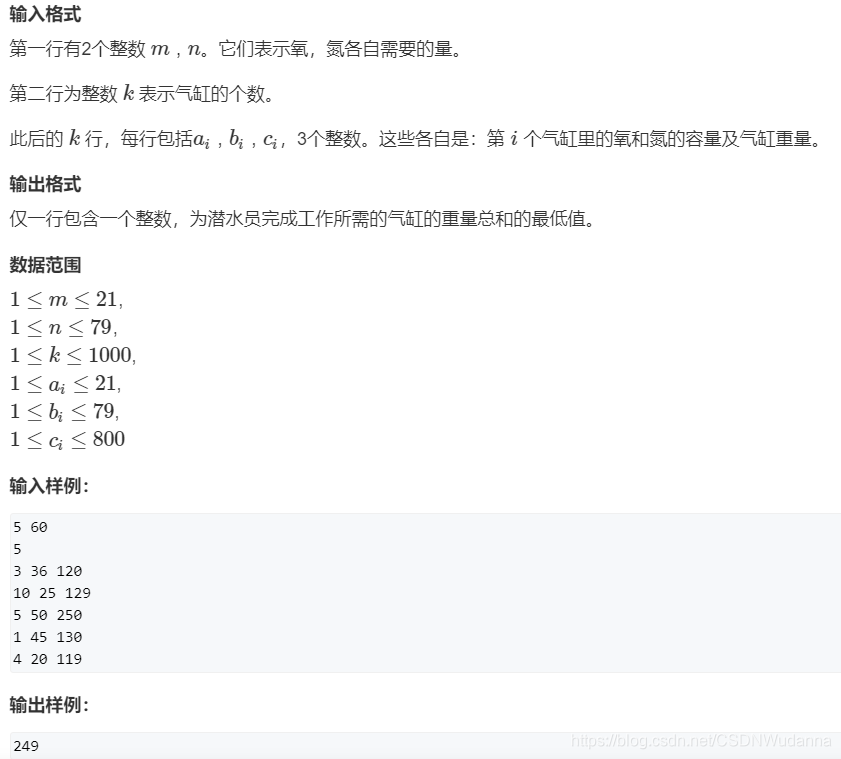
【注意】
和一般的 01 背包的区别在于,这里就算气缸的氧气大于了目前的 j (氮气同理),也依然可以记录在当前的方案中,所以需要在循环的时候从 0 开始,表示氧气已足,单纯从 0 ~ k 的氮气要求量中考虑气缸。
#include<iostream>
#include<cstring>
using namespace std;
const int N = 1010, M = 85;
const int INF = 0x3f3f3f3f;
//dp[i][j][k] 表示 从前 i 件气缸挑选出氧气不小于 j、氮气不小于 k 的最小重量
int dp[N][M][M];
int main() {
int m, n, k;
cin >> m >> n >> k;
memset(dp, 0x3f, sizeof dp);
for (int i = 1; i <= k; ++ i) {
int a, b, c;
cin >> a >> b >> c;
//因为前面memset了,所以需要从 0 开始
for (int j = 0; j <= m; ++ j) {
for (int k = 0; k <= n; ++ k) {
int &x = dp[i][j][k];
x = dp[i - 1][j][k]; //不拿第 i 件气缸
// 拿第 i 件气缸就足够了
if (a >= j && b >= k) x = min(x, c);
//拿第 i 件气缸但是还不足够
else {
int p = max(0, j - a); //下标不能为负
int q = max(0, k - b);
x = min(x, dp[i - 1][p][q] + c);
}
}
}
}
cout << dp[k][m][n];
return 0;
}
6、AcWing 1013. 机器分配 :求具体方案
原题链接:https://www.acwing.com/problem/content/1015/

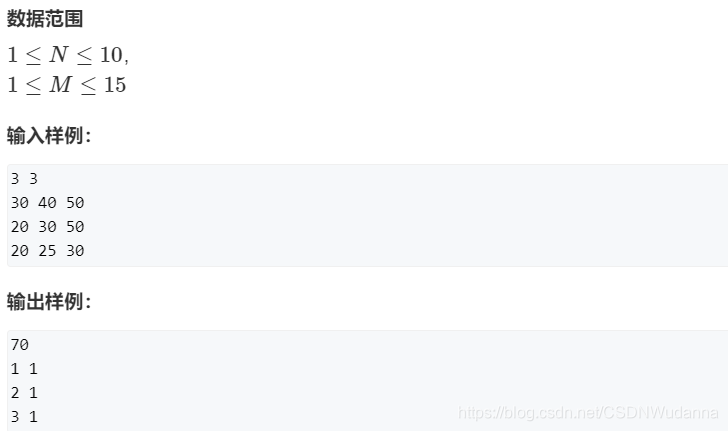
【解法一 :DP】
主要是标记本步骤是用了还是没用。
#include<iostream>
using namespace std;
const int N = 20;
int dp[N][N]; //dp[i][j] 表示前 i 家公司,共获得 j 台设备的最大最终获利
int val[N][N]; //保存数据,val[i][j]表示第 i 家公司获得 j 台设备的获利
//st[i][j][k] 表示在前 i 家公司中,共获得 j 台设备,且第 i 家公司是否获得 k 台设备
bool st[N][N][N];
int res[N]; //最终方案,res[i] 表示第 i 家公司获得res[i]台设备
int main() {
int n, m;
cin >> n >> m;
//枚举第几家公司
for (int i = 1; i <= n; ++ i) {
//枚举设备数目
for (int j = 1; j <= m; ++ j) {
cin >> val[i][j];
dp[i][j] = dp[i - 1][j]; //这家公司获得0台设备
//枚举第 i 家公司获得 1 ~ j 台设备
for (int k = 1; k <= j; ++ k) {
if (dp[i - 1][j - k] + val[i][k] > dp[i][j]) {
dp[i][j] = dp[i - 1][j - k] + val[i][k];
st[i][j][k] = true; //标记
}
}
}
}
cout << dp[n][m] << endl; //最大利润
//从后往前推出路径
int a = n, b = m;
while (a && b > 0) {
//因为在前面dp的时候是从1~m,越往后说明后面的方案能获得更大的利润
//所以这里需要反着来
for (int i = m; i >= 1; -- i) {
if (st[a][b][i]) {
res[a] = i;
b -= i;
break;
}
}
-- a;
}
//输出方案
for (int i = 1; i <= n; ++ i) {
cout << i << " " << res[i] << endl;
}
return 0;
}
【解法二 :搜索】
#include<iostream>
using namespace std;
const int N = 20;
int n, m;
int ans = 0;
int nums[N][N];
int res[N], temp[N];
//给第son家子公司分配时,剩下sum个设备,分配前已经获得利益为val
void dfs(int son, int sum, int val) {
if (sum == 0) {
if (ans < val) {
ans = val;
for (int i = 1; i <= n; ++ i) res[i] = temp[i];
}
}
else if (son > n) return;
else {
for (int i = 0; i <= sum; ++ i) {
temp[son] = i;
dfs(son + 1, sum - i, val + nums[son][i]);
temp[son] = 0; //恢复现场
}
}
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; ++ i) {
for (int j = 1; j <= m; ++ j)
cin >> nums[i][j];
}
dfs(1, m, 0);
cout << ans << endl;
for (int i = 1; i <= n; ++ i) cout << i << " " << res[i] << endl;
return 0;
}
7、AcWing 12. 背包问题求具体方案 :求字典序最小的具体方案
原题链接:https://www.acwing.com/problem/content/description/12/

#include<iostream>
using namespace std;
const int N = 1010;
int dp[N][N];
int v[N], w[N]; //保存数据
bool st[N][N]; //st[i][j] 表示状态dp[i][j]是否使用了第i件物品
int ans[N]; //存放最终路径
int main() {
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; ++ i) cin >> v[i] >> w[i];
for (int i = n; i >= 1; -- i) {
for (int j = 1; j <= m; ++ j) {
dp[i][j] = dp[i + 1][j];
if (v[i] <= j) {
int num = dp[i + 1][j - v[i]] + w[i];
if (dp[i][j] <= num) { //如果用方法二获得ans数组,可以dp[i][j] < num
dp[i][j] = num;
st[i][j] = true;
}
}
}
}
int k = 0;
//方法一:使用st数组
int a = 1, b = m;
while (a <= n && b) {
if (st[a][b]) {
ans[k ++] = a;
b -= v[a];
}
++ a;
}
/*
//方法二:不需要st数组
int a = 1, b = m;
while (a <= n && b) {
if (b >= v[a] && dp[a][b] == dp[a + 1][b - v[a]] + w[a]) {
ans[k ++] = a;
b -= v[a];
}
++ a;
}
*/
for (int i = 0; i < k; ++ i) cout << ans[i] << " ";
return 0;
}
8、AcWing 11. 背包问题求方案数 :求最优解的方案数

#include<iostream>
using namespace std;
const int N = 1010;
const int modd = 1e9 + 7;
#define ll long long
struct node{
ll val, cnt; //val-最大价值 cnt-方案数
}dp[N][N];
int main() {
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; ++ i) {
int v, w;
cin >> v >> w;
for (int j = 1; j <= m; ++ j) {
//不包含第 i 件物品
dp[i][j].val = dp[i - 1][j].val;
dp[i][j].cnt = dp[i - 1][j].cnt;
//包括第 i 件物品
if (v <= j) {
if (dp[i][j].val < dp[i - 1][j - v].val + w) {
dp[i][j].val = dp[i - 1][j - v].val + w;
//由于+w,防止dp[i - 1][j - v].val == 0导致的dp[i - 1][j - v].cnt == 0
dp[i][j].cnt = max((int)dp[i - 1][j - v].cnt, 1);
}
else if (dp[i][j].val == dp[i - 1][j - v].val + w)
//不包含 i 和包含 i 的方案数相加
dp[i][j].cnt += max(dp[i - 1][j - v].cnt, 1ll);
dp[i][j].cnt %= modd;
}
}
}
cout << dp[n][m].cnt;
return 0;
}
9、AcWing 487. 金明的预算方案 :二进制枚举构造分组背包的决策
原题链接:https://www.acwing.com/problem/content/description/489/

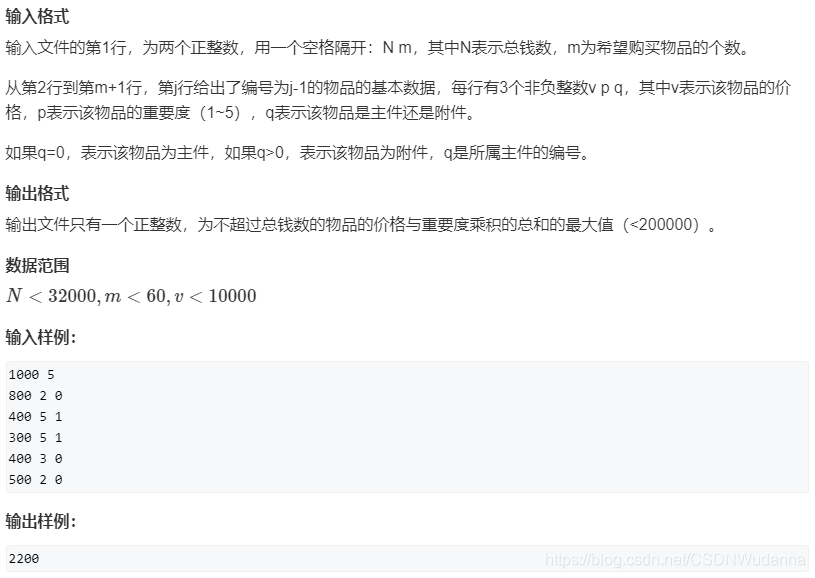
/*
把每一套主附件都看成一组,这就是一个分组背包。
储存数据的时候用vector数组方便获得附件的数量。
求解方案的时候可以用二进制枚举。
*/
#include<iostream>
#include<vector>
#include<cmath>
using namespace std;
const int N = 70, M = 32010;
struct node{
int v = 0, w = 0;
};
int dp[N][M];
node major[N];
vector<node> minor[N];
int main() {
int m, n;
cin >> m >> n;
for (int i = 1; i <= n; ++ i) {
int v, w, q;
cin >> v >> w >> q;
w *= v;
if (!q) {
major[i] = {v, w};
}
else {
minor[q].push_back({v, w});
}
}
//枚举第i组
for (int i = 1; i <= n; ++ i) {
// if (major[i].v > 0) {
int num = minor[i].size(); //附件数量
int length = pow(2, num); //主附件搭配方案数量
//枚举钱有多少
for (int j = 1; j <= m; ++ j) {
//无论major[i].v是否大于0都需要更新dp数组
//所以最外面那个if不能加上,否则会断层
dp[i][j] = dp[i - 1][j]; //不要第i组
if (major[i].v <= j) {
//枚举主附件搭配方案
for (int k = 0; k < length; ++ k) {
int v = major[i].v, w = major[i].w;
//获取搭配方案由哪几件构成
for (int p = 0; p < num; ++ p) {
if ((k >> p) & 1) {
v += minor[i][p].v;
w += minor[i][p].w;
}
}
//要第i组
if (v <= j) dp[i][j] = max(dp[i][j], dp[i - 1][j - v] + w);
}
}
}
// }
}
cout << dp[n][m];
return 0;
}
10、AcWing 10. 有依赖的背包问题 :树形套分组
原题链接https://www.acwing.com/problem/content/10/
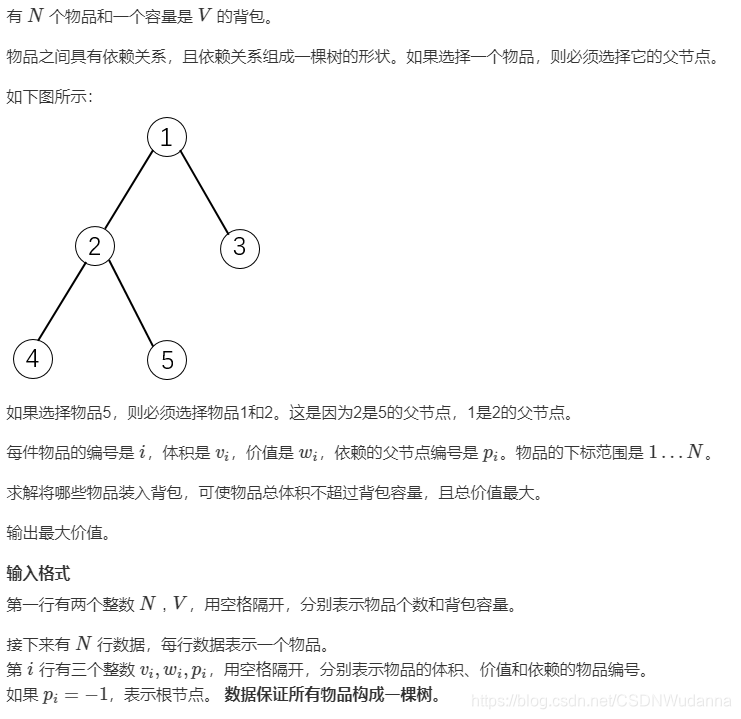

1、为什么dfs的第二层循环j需要从大到小?
首先在分组背包的板题里面是小到大或者从大到小都可以的。
因为dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i][k]] + w[i][k]);
我们可以发现,i代表前i组,在状态转移时无论j从小开始还是大开始,需要用到的状态已经是上一轮计算过的,不会影响最终结果。
(同理,即便把最外层循环和次外层循环互换也不影响结果)
但是反观这道题,在表示状态的时候其实隐含了另外一层意思,这里不再是dp[i][j],而是dp[u][j]了。
dp[u][j]表示的是以u为根节点的子树,在不超过j体积前提下获得的最大价值。
在状态转移时,dp[u][j] = max(dp[u][j], dp[u][j - k] + dp[son][k]);
我们可以发现,转移时会用到本轮会计算的状态dp[u][j - k],而不像板题那样时u-1。
如果j从小到大,那么当dp[u][2]已经更新过了,dp[u][4]在状态转移时用到了dp[u][2],可能会重复使用物品组。
所以我们需要j从大到小,这样保证了同一个物品组不会被选择多次,而是最多只有一次。
2、为什么dfs三层循环的i和j不能互换?
在分组背包的板题 https://www.acwing.com/problem/content/9/ 是可以互换的。
可以互换的原因和第1点类似(但不太一样),是因为转移的状态不是当前这一轮的,能保证需要用到的状态都是已经计算好的。
但其实一开始我钻了好久的牛角尖,因为我会觉得u是指以u为根节点的子树,并不像板题那样代指前u组,在dp[u][j]里面并没有体现前i组的概率。
在先i再j再k的顺序所代表的逻辑已经在代码里面写明了,但是不知道有没有朋友和我有同样的疑惑:
先i再j再k表示从h[u]到e[i]的物品组使用了不超过j体积、且物品组e[i]使用不超过k体积所能获得的最大体积,
那么先j再i再k(这里会先做第3点预处理dfs)对应的应该是表示一共不超过j体积的前提下,只考虑从h[u]到e[i]的物品组,且物品组e[i]使用不超过k体积所能获得的最大体积。
乍一想好像没毛病,但是一直wa,改了很多版也ac不了。
再细想一下,好像我把状态转移的过程和树形脱离开了,这是一个树形套分组的dp,而不是纯分组。
状态转移时,是以子树为单位转移,如果循环的时候先枚举体积再枚举u的后继,可能子树之间会交叉转移状态。
之所以用“可能”这样的字眼,是因为我自己也不是百分百确定,如果有大佬能不吝赐教,真的万分感谢!!我已经困扰好久了
3、可以先独立一个循环先dfs再三个循环去dp吗?
可以。
因为我们是走到叶节点才开始处理dp过程的,而每一棵子树又是互相独立的物品组,所以这两者是等价的。
实例:
void dfs(int u)
{
for (int i = h[u]; ~i; i = ne[i]) // 循环物品组
dfs(e[i]);
//为什么不能交换i、j?
for (int i = h[u]; ~i; i = ne[i]) {
for (int j = m - v[u]; j >= 0; j --) // 循环物品组
{
int son = e[i];
for (int k = 0; k <= j; k ++ ) // 循环决策
{
f[u][j] = max(f[u][j], f[u][j - k] + f[son][k]);
}
}
}
…………
}
4、ac代码
#include<iostream>
#include<cstring>
using namespace std;
const int N = 110;
//dp[u][j]表示以u为根节点的子树,在不超过j体积前提下获得的最大价值
int dp[N][N], v[N], w[N];
int n, m;
int h[N], e[N], ne[N], idx = 1;
void insert(int a, int b) {
e[idx] = b;
ne[idx] = h[a];
h[a] = idx ++;
}
void dfs(int u) {
//把u的每一个后继看成一个个独立的物品组
//枚举第i个物品组 == 枚举u的后继i
for (int i = h[u]; i != -1; i = ne[i]) {
int son = e[i];
dfs(son);
//枚举体积:j表示给从h[u]到son的后继一共分配j体积
for (int j = m - v[u]; j > 0; -- j) {
//枚举决策:k表示这j体积里面有k体积是给后继son的
for (int k = 0; k <= j; ++ k) {
//dp[u][j] = max(不要son这个物品组, 要son这个物品组);
dp[u][j] = max(dp[u][j], dp[u][j - k] + dp[son][k]);
}
}
}
//把从0 ~ m - v[u] 往后挪 v[u] 个长度,因为必须加上根节点u
for (int j = m; j >= v[u]; -- j) dp[u][j] = dp[u][j - v[u]] + w[u];
//把放不下根节点u的状态清0
for (int j = 0; j < v[u]; ++ j) dp[u][j] = 0;
}
int main() {
cin >> n >> m;
int root;
memset(h, -1, sizeof h);
for (int i = 1; i <= n; ++ i) {
int p;
cin >> v[i] >> w[i] >> p;
if (p != -1) insert(p, i);
else root = i;
}
dfs(root);
cout << dp[root][m];
return 0;
}
11、AcWing 734. 能量石 :贪心+变种01
原题链接:https://www.acwing.com/problem/content/description/736/



【思路:贪心 + 变种01背包】
这个问题的解集由两个问题共同构成:① 挑选哪些能量石 ② 挑选的能量石以何种顺序食用
如果直接dp时间铁爆,所以我们需要先把解集缩小。
借鉴贪心的思想,假如最优解中存在两块排序相邻的能量石设为 i、i+1。
那么由于设定最优解是先吃i再吃i+1,那么得到的能量是 Ei’ + Ei+1’ - Si * Li+1.
(其中 Ei’、Ei+1’ 分别表示在吃i时能量石i和i+1剩余的能量)
假设先吃 i+1 再吃 i,那么获得的能量是 Ei+1’ + Ei’ - Si+1 * Li.
由此可得Si * Li+1 <= Si+1 * Li,这样先吃i才会是最优解。
故而,最优解的能量石顺序一定是遵循si/li小的排在前面的规则。
故而此时只剩下问题①:挑选哪些能量石
这里可以直接01背包求。
但需要注意的是这是一个变种的01背包,第i块能量石的价值会随j改变。
所以需要对过程的每一个dp[i][j]取max。
解法一:j表示不超过
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 110, M = 10010;
//dp[i][j]表示在已经排好序的前 i 块能量石中,消耗不超过 j 时间的最大价值
int dp[N][M];
struct node{
int s, e, l;
}arr[N];
bool cmp(node a, node b) {
return a.s * b.l < b.s * a.l;
}
int main() {
int t;
cin >> t;
for (int k = 1; k <= t; ++ k) {
int n, m = 0;
cin >> n;
for (int i = 1; i <= n; ++ i) {
int s, e, l;
cin >> s >> e >> l;
arr[i] = {s, e, l};
m += s; //因为l可能为0,所以需要叠加时间
}
sort(arr + 1, arr + n + 1, cmp);
int ans = 0;
for (int i = 1; i <= n; ++ i) {
int s = arr[i].s, e = arr[i].e, l = arr[i].l;
for (int j = 0; j <= m; ++ j) {
dp[i][j] = dp[i - 1][j]; //这里决定了不用memset置零,因为会被dp[0][x]置零
//因为j是表示不超过,所以需要对0取max,毕竟是在不超过中取最优解
if (s <= j) dp[i][j] = max(dp[i][j], dp[i - 1][j - s] + max(0, e - l * (j - s)));
ans = max(ans, dp[i][j]); //能量石会贬值,不是单纯的01背包,是以需要取max
}
}
cout <<"Case #" << k << ": " << ans << endl;
}
return 0;
}
解法二:j表示恰好
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 110, M = 10010;
//dp[i][j]表示在已经排好序的前 i 块能量石中,消耗恰好为 j 时间的最大价值
int dp[N][M];
struct node{
int s, e, l;
}arr[N];
bool cmp(node a, node b) {
return a.s * b.l < b.s * a.l;
}
int main() {
int t;
cin >> t;
for (int k = 1; k <= t; ++ k) {
int n, m = 0;
cin >> n;
for (int i = 1; i <= n; ++ i) {
int s, e, l;
cin >> s >> e >> l;
arr[i] = {s, e, l};
m += s; //因为l可能为0,所以需要叠加时间
}
sort(arr + 1, arr + n + 1, cmp);
int ans = 0;
memset(dp, -0x3f, sizeof dp); //eg.dp[0][6]是不合法的,所以初始化为负无穷
dp[0][0] = 0;
for (int i = 1; i <= n; ++ i) {
int s = arr[i].s, e = arr[i].e, l = arr[i].l;
for (int j = 0; j <= m; ++ j) {
dp[i][j] = dp[i - 1][j];
//因为是j表示为恰好,所以不能对0取max,因为恰好就是必须包上第i颗能量石在时间j的真实情况
if (s <= j) dp[i][j] = max(dp[i][j], dp[i - 1][j - s] + e - l * (j - s)));
ans = max(ans, dp[i][j]); //能量石会贬值,不是单纯的01背包,所以需要取max
}
}
cout <<"Case #" << k << ": " << ans << endl;
}
return 0;
}







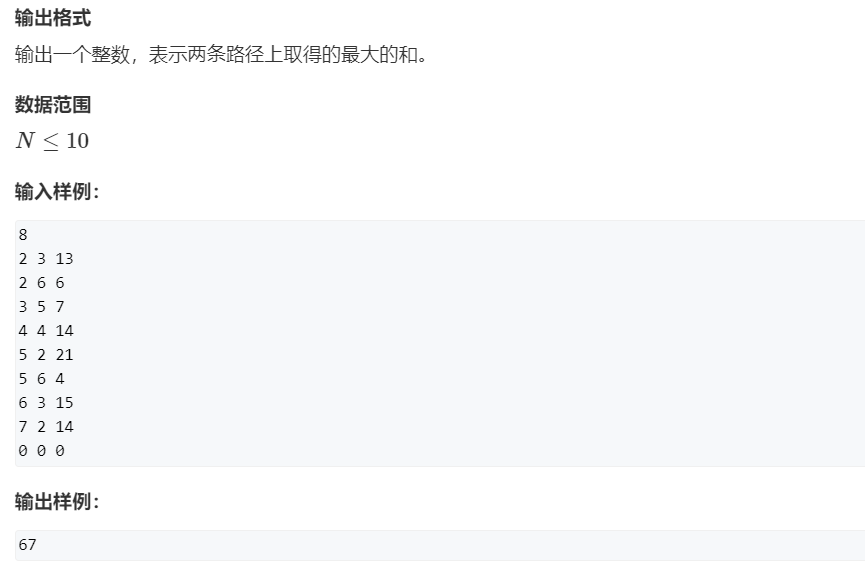

















 1833
1833

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








