const int limit=5e5;
const int N=5e5+5;
int n,m,t;
int i,j,k;
int a[N];
struct Node
{
int l, r;
int sum;
}node[N<<2];// 4 倍
void build(int id,int l,int r)
{
node[id].l=l,node[id].r=r;
if(l==r) node[id].sum=a[l];
else{
int mid=l+r>>1;
build(id<<1,l,mid);
build(id<<1|1,mid+1,r);
node[id].sum=node[id<<1].sum+node[id<<1|1].sum;
}
}
void update(int id,int pos,int val)
//从 1 节点向下寻找
{
if(node[id].l==node[id].r){
node[id].sum+=val;
return ; //注意
}
int mid=node[id].l+node[id].r>>1;
if(pos<=mid){
update(id<<1,pos,val);
}
else{
update(id<<1|1,pos,val);
}
node[id].sum=node[id<<1].sum+node[id<<1|1].sum;
}
int query(int id,int l,int r)
//从 1 节点向下寻找
{
if(node[id].l==l && node[id].r==r) return node[id].sum;
int mid=node[id].l+node[id].r>>1;
if(r<=mid){ //目标区间全部在左儿子上
return query(id<<1,l,r);
}
else if(l>=mid+1){ //目标区间全部在右儿子上
return query(id<<1|1,l,r);
}
else{ //目标区间在左儿子和右儿子上都有
return query(id<<1,l,mid)+query(id<<1|1,mid+1,r);
}
}
int main()
{
//IOS;
while( ~sdd(n,m) ){
for(i=1;i<=n;i++) sd(a[i]);
build(1,1,limit);
while(m--){
int tag,x,y;
sddd(tag,x,y);
if(tag==1){
update(1,x,y);
}
else{
pd(query(1,x,y));
}
}
}
//PAUSE;
return 0;
}






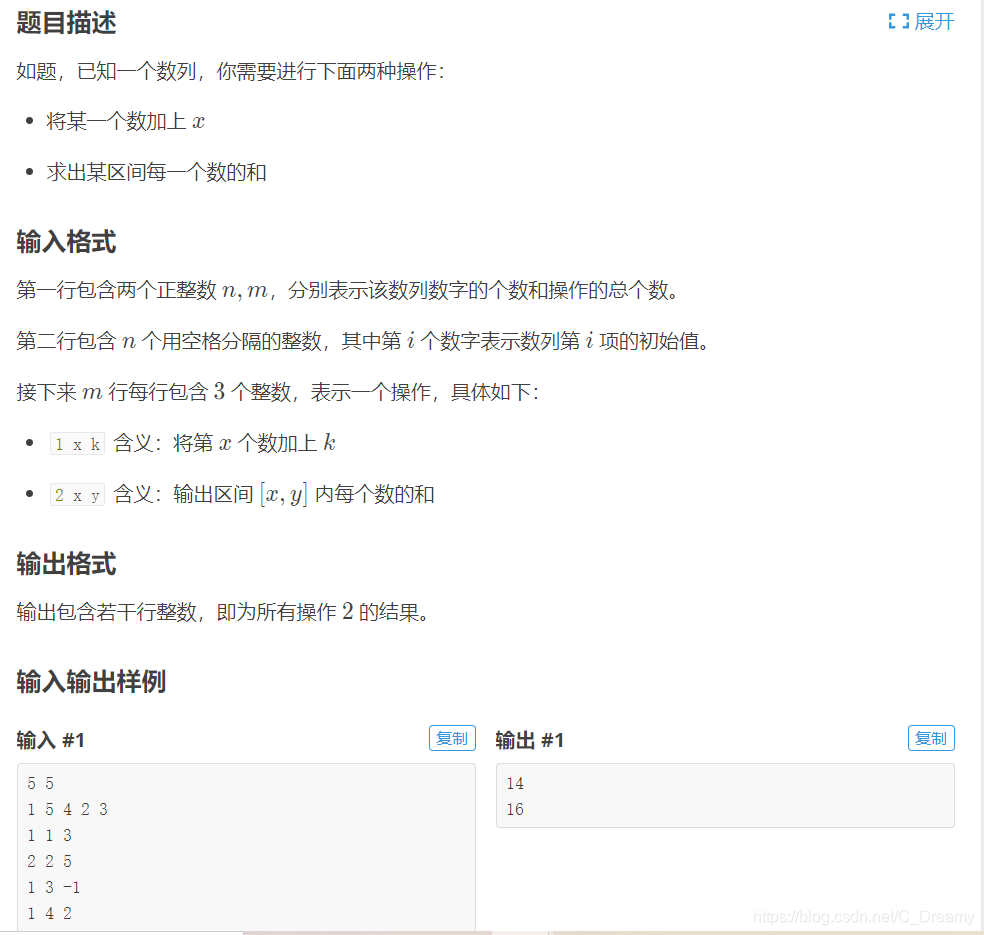
 本文详细介绍了一种基于段式树状数组的数据结构实现方法,包括构建、更新和查询操作的具体算法。通过递归的方式,该方法能够高效地处理数组的区间修改和区间求和等问题,适用于动态规划和算法竞赛等场景。
本文详细介绍了一种基于段式树状数组的数据结构实现方法,包括构建、更新和查询操作的具体算法。通过递归的方式,该方法能够高效地处理数组的区间修改和区间求和等问题,适用于动态规划和算法竞赛等场景。
















 131
131

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








