量子相位估计(Quantum Phase Estimation, QPE)是一种用于测量一个量子态的相位的算法。QPE算法的核心是一个相位估计电路,其中包含了一系列Hadamard变换、控制相位旋转门和逆量子傅里叶变换等量子门。其中,控制相位旋转门是QPE算法的重要组成部分,而T门是最常用的控制相位旋转门之一。通过施加T门,我们可以将任意一个量子态的相位旋转一个固定的角度 θ = π / 4 \theta = \pi/4 θ=π/4。因此,在量子相位估计中,我们可以将待求相位所对应的幂级数展开,然后利用控制相位旋转门,将待求相位所对应的相位旋转成一个能够处理的角度。然后,我们可以通过逆量子傅里叶变换将相位转化为一个整数,从而得到待求相位。
1.准备量子态:我们首先需要准备一个包含待求相位的量子态。这个量子态可以是一个本征态,或者是通过量子相位估计算法中的特定构造方法得到的量子态。
2.施加Hadamard变换:对于一个n比特的量子态,我们需要施加n个Hadamard变换,将这些量子比特转化为等概率分布的态。
3.控制相位旋转门:接下来,我们需要施加控制相位旋转门,将待求相位所对应的幂级数展开成一个相位旋转角度。在QPE算法中,最常用的控制相位旋转门是T门,它可以将相位旋转一个角度 θ = π / 4 \theta = \pi/4 θ=π/4。
4.逆量子傅里叶变换:接下来,我们需要进行逆量子傅里叶变换,将测量结果转化为一个整数,从而得到待求相位的近似值。
通过上述步骤,我们可以利用T门和其他量子门实现量子相位估计,从而求解许多重要的量子计算问题,例如求解Shor算法中的大数分解问题等。
在量子相位估计算法中,我们需要使用Controlled Unitary门将待求本征态的相位信息编码到辅助量子比特中。这个Controlled Unitary门由一个控制量子比特和一个目标量子比特组成,其中目标量子比特是待求本征态,控制量子比特用于施加一个相位旋转门。
相位估计算法的基本原理是利用量子相干性质,在不同的本征值上给辅助量子比特施加不同的相位旋转,使得最终测量结果可以反映出待求本征态的相位信息。我们将使用一个包含多个控制T门的量子电路,其中控制量子比特是辅助量子比特,目标量子比特是待求本征态的量子比特。这个电路会在辅助量子比特上施加一系列不同的相位旋转,使得待求本征态的相位信息被编码到辅助量子比特上。然后,我们测量辅助量子比特的状态,从而可以得到待求本征态的相位信息。相位估计算法是量子计算中的重要算法之一,它可以应用于许多领域,例如化学计算、密码学和优化问题等。
Controlled Unitary
Controlled Unitary是一种量子门,它是一个控制门和一个单量子比特门的组合。在这个代码中,Controlled Unitary是一个由控制量子比特和目标量子比特组成的控制门和T门组合构成的门,它用于量子相位估计算法(QPE)中的第二步。这个Controlled Unitary门的作用是在目标量子比特上施加一个相位旋转门,其旋转角度取决于控制量子比特的状态。
在这个代码中,我们使用for循环实现了这个Controlled Unitary门。我们对辅助量子寄存器qr_aux中的每个量子比特进行迭代,使用嵌套的for循环对不同的二进制位进行迭代。对于每个二进制位,我们将辅助量子比特和本征量子比特作为控制门和目标门,然后使用cp门(控制相位门)施加一个相位旋转门。其中,旋转角度是π/4,即T门的旋转角度。
这个Controlled Unitary门的作用是在量子相位估计算法中的第二步,将待求本征态的相位信息编码到辅助量子比特中。在这个步骤中,我们将目标量子比特设置为待求本征态,将辅助量子比特设置为控制量子比特,并使用Controlled Unitary门在待求本征态上施加一个相位旋转门。这个门的作用是将待求本征态的相位信息编码到辅助量子比特上,使得待求本征态的相位可以通过测量辅助量子比特的状态来获取。
本征态是指一个量子系统在特定测量下得到确定结果的量子态。对于一个已知的本征态,我们可以通过相位估计算法来计算其对应的本征值。在量子计算中,我们需要将本征态从
∣
0
⟩
|0\rangle
∣0⟩转换为
∣
1
⟩
|1\rangle
∣1⟩,使用X门可以实现这一转换。我们需要将
∣
0
⟩
|0\rangle
∣0⟩取反,即
X
∣
0
⟩
=
∣
1
⟩
X|0\rangle=|1\rangle
X∣0⟩=∣1⟩,以便后续使用量子相位估计算法。在QPE算法中,我们需要将辅 助量子比特制备成所有可能的本征值的叠加态,这样我们就可以对待求本征态的相位进行估计。将辅助量子比特制备成叠加态的方法是在辅助量子比特上应用Hadamard门,这将使辅助量子处于叠加态中,其中|0⟩和|1⟩表示辅助量子比特的两个基态。
# Code for QPE with T-gate (θ=0.001 base 2)
qr_aux = QuantumRegister(3, 'aux')
qr_eigen = QuantumRegister(1, 'eigen')
cr = ClassicalRegister(3, 'aux_read')
qc = QuantumCircuit(qr_aux, qr_eigen, cr)
# Prepare eigenstate
qc.x(qr_eigen)
qc.barrier()
# QPE - step 1: Superposition
qc.h(qr_aux)
qc.barrier()
# QPE - step 2: Controlled Unibary
for idx in np.arange(len(qr_aux)):
for digit in np.arange(2**idx):
qc.cp(np.pi/4, qr_aux[idx], qr_eigen)
qc.barrier()
# QPE - step 3: Inverse QFT
qft_dagger(qc, len(qr_aux))
qc.barrier()
# QPE - step 4: Measurement
qc.measure(qr_aux, cr)
qc.draw()
由于电路图特别长,这边就不上图了。使用这个方法我们就可以通过测量辅助比特(3位)来估计特征值(0~7)范围内的一个整数。
结果如下
这个值是三个辅助比特的测量结果,可以用来估计特征值。
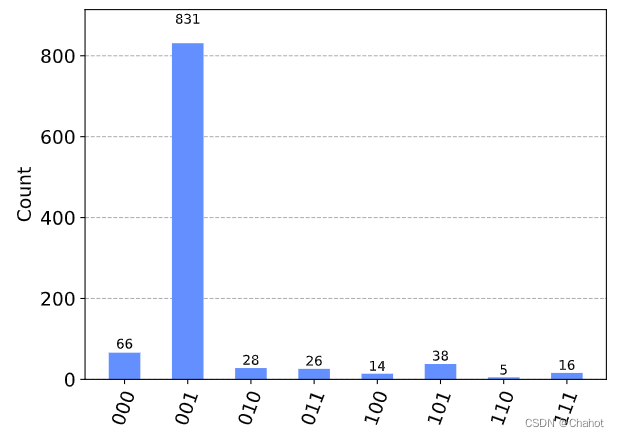
在量子相位估计算法中,我们需要将一个控制相位门( U U U门)作用于一个特定的特征态上,以获取该特征态的相位信息。该特征态由一个特征向量和相应的特征值所定义。
在这个示例中,我们已经将特征向量 ∣ 1 ⟩ |1\rangle ∣1⟩ 准备好,并将其存储在名为 qr_eigen 的量子寄存器中。我们将施加控制相位门 U = e 2 π i θ = e i π T U=e^{2\pi i \theta} = e^{i\pi T} U=e2πiθ=eiπT 来准备特征态,并使用 n n n 个辅助量子比特来估计相位角度 θ \theta θ。在 QPE 算法中,我们需要对这 n n n 个辅助比特进行测量,以获得一个 n n n 位的二进制测量结果。将这些测量结果解释为一个 n n n 位二进制数,并将其除以 2 n 2^n 2n,就得到了一个估计的相位 θ ~ \tilde{\theta} θ~。这个相位 θ ~ \tilde{\theta} θ~ 与特征值之间存在某种关系,这种关系取决于所用的特征向量和相应的特征值。
在这个例子中,我们在 ∣ 1 ⟩ |1\rangle ∣1⟩ 上施加了 T T T 门, T T T 门的特征值为 e i π / 4 e^{i\pi/4} eiπ/4,因此在我们的量子电路中,特征值的相位是 e i π / 4 e^{i\pi/4} eiπ/4。注意到 e i π / 4 e^{i\pi/4} eiπ/4 和 1 / 2 ( 1 + i ) 1/\sqrt{2}(1+i) 1/2(1+i) 的值是等价的。这是因为 e i θ = cos ( θ ) + i sin ( θ ) e^{i\theta} = \cos(\theta) + i\sin(\theta) eiθ=cos(θ)+isin(θ),所以 e i π / 4 = cos ( π / 4 ) + i sin ( π / 4 ) = 1 / 2 ( 1 + i ) e^{i\pi/4} = \cos(\pi/4) + i\sin(\pi/4) = 1/\sqrt{2}(1+i) eiπ/4=cos(π/4)+isin(π/4)=1/2(1+i)。这是欧拉公式的结果,将复指数函数与三角函数联系起来。因此,我们可以将 e i π / 4 e^{i\pi/4} eiπ/4 表示为 1 / 2 ( 1 + i ) 1/\sqrt{2}(1+i) 1/2(1+i),这意味着我们的估计值实际上是对特征向量 ∣ 1 ⟩ |1\rangle ∣1⟩ 和 ∣ + ⟩ |+\rangle ∣+⟩ 的线性组合的估计,其中 ∣ + ⟩ |+\rangle ∣+⟩ 是一个等概率的叠加态,即 ∣ + ⟩ = 1 / 2 ( ∣ 0 ⟩ + ∣ 1 ⟩ ) |+\rangle = 1/\sqrt{2}(|0\rangle + |1\rangle) ∣+⟩=1/2(∣0⟩+∣1⟩)。这样,我们就可以将估计值解释为特征向量 ∣ 1 ⟩ |1\rangle ∣1⟩ 的贡献和特征向量 ∣ + ⟩ |+\rangle ∣+⟩ 的贡献的加权平均值,其中 ∣ 1 ⟩ |1\rangle ∣1⟩ 的贡献系数是 1 / 2 1/\sqrt{2} 1/2, ∣ + ⟩ |+\rangle ∣+⟩ 的贡献系数是 1 / 2 1/\sqrt{2} 1/2。因此,估计值与特征向量 ∣ 1 ⟩ |1\rangle ∣1⟩ 的关系是一个线性组合的形式。其中, θ \theta θ 是通过相位估计获得的特征值的相位。这个线性组合的系数正是特征向量 ∣ 1 ⟩ |1\rangle ∣1⟩ 的系数。 1 2 \frac{1}{\sqrt{2}} 21 是 ∣ 0 ⟩ |0\rangle ∣0⟩ 的系数, e i θ e^{i\theta} eiθ 是 ∣ 1 ⟩ |1\rangle ∣1⟩ 的系数。因此,估计值 θ \theta θ 可以视为特征向量 ∣ 1 ⟩ |1\rangle ∣1⟩ 在 ∣ + ⟩ |+\rangle ∣+⟩ 和 ∣ − ⟩ |-\rangle ∣−⟩ 基础上的线性组合系数。因为特征向量 ∣ 1 ⟩ |1\rangle ∣1⟩ 是由 ∣ + ⟩ |+\rangle ∣+⟩ 和 ∣ − ⟩ |-\rangle ∣−⟩ 通过 H H H 门的作用得到的。 ∣ 1 ⟩ = ( ∣ 0 ⟩ − ∣ 1 ⟩ ) / 2 = ( ∣ + ⟩ − ∣ − ⟩ ) / 2 |1\rangle=(|0\rangle-|1\rangle)/\sqrt{2} = (|+\rangle-|-\rangle)/\sqrt{2} ∣1⟩=(∣0⟩−∣1⟩)/2=(∣+⟩−∣−⟩)/2。因此,我们可以将估计值写为 ∣ 1 ⟩ |1\rangle ∣1⟩ 和 ∣ 0 ⟩ |0\rangle ∣0⟩ 的线性组合形式,即 ∣ ψ ⟩ = α ∣ 0 ⟩ + β ∣ 1 ⟩ |\psi\rangle = \alpha|0\rangle + \beta|1\rangle ∣ψ⟩=α∣0⟩+β∣1⟩,其中 α \alpha α 和 β \beta β 分别为估计值对应的二进制小数的整数和分数部分。
根据之前的计算,特征值的相位为
e
i
π
/
4
e^{i\pi/4}
eiπ/4。因为测量结果为
001
001
001,这相当于将二进制小数
0.001
0.001
0.001 转化为十进制数,即
0
×
2
−
1
+
0
×
2
−
2
+
1
×
2
−
3
=
0.125
0\times 2^{-1}+0\times 2^{-2}+1\times 2^{-3}=0.125
0×2−1+0×2−2+1×2−3=0.125。由于相位为
e
i
π
/
4
e^{i\pi/4}
eiπ/4,因此可以将其表示为
e
i
(
2
π
)
(
1
/
8
)
=
e
i
π
/
4
e^{i(2\pi)(1/8)}=e^{i\pi/4}
ei(2π)(1/8)=eiπ/4,与之前计算的相位相同。这里的0.001是指以二进制表示时,角度为
1
1000
\frac{1}{1000}
10001,也就是对应的特征值相位为
2
π
2
12
≈
0.001
\frac{2\pi}{2^{12}}\approx0.001
2122π≈0.001. 而001则是指最终测量结果,表示的是三个辅助比特的测量值。
在这个例子中,我们通过将辅助比特的测量结果转换为一个二进制小数来估计特征值。如果我们得到测量结果
∣
b
2
b
1
b
0
⟩
|b_2 b_1 b_0\rangle
∣b2b1b0⟩,那么我们可以将它转换为十进制小数
b
2
2
1
+
b
1
2
2
+
b
0
2
3
\frac{b_2}{2^1}+\frac{b_1}{2^2}+\frac{b_0}{2^3}
21b2+22b1+23b0。
在本例中,测量结果为 ∣ 001 ⟩ |001\rangle ∣001⟩,因此我们可以将它转换为 0 2 1 + 0 2 2 + 1 2 3 = 0.125 \frac{0}{2^1}+\frac{0}{2^2}+\frac{1}{2^3}=0.125 210+220+231=0.125。而这个值与 2 π × 0.125 = 0.25 π 2\pi\times0.125=0.25\pi 2π×0.125=0.25π 相差一个常数因子,因此最终特征值的相位为 e i 0.25 π = 2 2 + 2 2 i e^{i0.25\pi}=\frac{2}{\sqrt{2}}+\frac{2}{\sqrt{2}}i ei0.25π=22+22i。
这个公式是量子相位估计算法的输出状态表示。在量子相位估计算法中,首先准备一个初始状态
∣
ψ
⟩
=
1
2
(
∣
0
⟩
+
∣
1
⟩
)
|\psi\rangle=\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)
∣ψ⟩=21(∣0⟩+∣1⟩),并在第一个比特上施加
T
T
T 门,得到状态
1
2
(
∣
0
⟩
+
e
i
π
/
4
∣
1
⟩
)
\frac{1}{\sqrt{2}}(|0\rangle+e^{i\pi/4}|1\rangle)
21(∣0⟩+eiπ/4∣1⟩)。施加
T
T
T 门相当于在 Bloch 球上沿着
z
z
z 轴旋转了
π
/
4
\pi/4
π/4 的角度。我们先考虑
∣
0
⟩
|0\rangle
∣0⟩,它在 Bloch 球上的表示是一个指向
+
z
+z
+z 方向的矢量。施加
T
T
T 门相当于将 Bloch 球上的
z
z
z 轴旋转了
π
/
4
\pi/4
π/4 的角度,此时矢量指向
x
x
x 和
z
z
z 的正半轴的平面内,即
1
2
(
∣
0
⟩
+
∣
1
⟩
)
\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)
21(∣0⟩+∣1⟩)。对于
∣
1
⟩
|1\rangle
∣1⟩,它在 Bloch 球上的表示是一个指向
−
z
-z
−z 方向的矢量,而在 Bloch 球上进行
π
/
4
\pi/4
π/4 的
z
z
z 轴旋转后,矢量指向的是
−
x
-x
−x 和
z
z
z 的负半轴的平面内,即
−
i
1
2
(
∣
0
⟩
−
∣
1
⟩
)
-i\frac{1}{\sqrt{2}}(|0\rangle-|1\rangle)
−i21(∣0⟩−∣1⟩)。因此,
T
T
T 门的作用将
∣
0
⟩
|0\rangle
∣0⟩ 和
∣
1
⟩
|1\rangle
∣1⟩ 线性组合,得到了
1
2
(
∣
0
⟩
+
e
i
π
/
4
∣
1
⟩
)
\frac{1}{\sqrt{2}}(|0\rangle+e^{i\pi/4}|1\rangle)
21(∣0⟩+eiπ/4∣1⟩) 这个状态。在初始状态
∣
0
⟩
|0\rangle
∣0⟩ 上施加
T
T
T 门,得到的新状态可以表示为
∣
0
⟩
|0\rangle
∣0⟩ 和
∣
1
⟩
|1\rangle
∣1⟩ 的线性组合。其中,
∣
0
⟩
|0\rangle
∣0⟩ 的系数为
1
2
\frac{1}{\sqrt{2}}
21,
∣
1
⟩
|1\rangle
∣1⟩ 的系数为
e
i
π
/
4
⋅
1
2
e^{i\pi/4}\cdot\frac{1}{\sqrt{2}}
eiπ/4⋅21,即
∣
1
⟩
|1\rangle
∣1⟩ 在新状态中的权重是一个复数,其相位为
π
/
4
\pi/4
π/4。因此,
T
T
T 门的作用是将
∣
0
⟩
|0\rangle
∣0⟩ 和
∣
1
⟩
|1\rangle
∣1⟩ 线性组合,得到了
1
2
(
∣
0
⟩
+
e
i
π
/
4
∣
1
⟩
)
\frac{1}{\sqrt{2}}(|0\rangle+e^{i\pi/4}|1\rangle)
21(∣0⟩+eiπ/4∣1⟩) 这个状态。
然后,将
n
n
n 个辅助比特初始化为
∣
0
⟩
|0\rangle
∣0⟩,并将它们与第一个比特通过控制
U
2
k
U^{2^k}
U2k 门相互作用。这个过程最终得到的输出状态为
∣
ψ
⟩
=
1
2
n
Σ
k
=
0
2
n
−
1
e
i
θ
k
∣
k
⟩
|\psi\rangle=\frac{1}{\sqrt{2^n}}\Sigma_{k=0}^{2^n-1}e^{i\theta_k}|k\rangle
∣ψ⟩=2n1Σk=02n−1eiθk∣k⟩
其中
θ
k
\theta_k
θk 表示特征向量
∣
u
⟩
|u\rangle
∣u⟩ 和控制相位门
U
2
k
U^{2^k}
U2k 的特征值的相位。根据这个公式,如果只有一个控制相位门作用于
∣
ψ
⟩
|\psi\rangle
∣ψ⟩,那么
∣
ψ
⟩
|\psi\rangle
∣ψ⟩ 可以写成如下形式:
∣
ψ
⟩
=
1
2
(
∣
0
⟩
+
e
i
θ
∣
1
⟩
)
|\psi\rangle=\frac{1}{\sqrt{2}}(|0\rangle+e^{i\theta}|1\rangle)
∣ψ⟩=21(∣0⟩+eiθ∣1⟩)
其中,
θ
\theta
θ 为控制相位门作用后的特征向量
∣
1
⟩
|1\rangle
∣1⟩ 的特征值的相位。因此,当只有一个控制相位门作用时,最终的输出状态可以表示为
∣
ψ
⟩
=
1
2
(
∣
0
⟩
+
e
i
π
T
∣
1
⟩
)
|\psi\rangle=\frac{1}{\sqrt{2}}(|0\rangle+e^{iπT}|1\rangle)
∣ψ⟩=21(∣0⟩+eiπT∣1⟩)
其中,
T
T
T 为控制相位门的矩阵,
e
i
π
T
e^{i\pi T}
eiπT 为特征值的相位。
当不止一个控制相位门时,我们使用的公式如下:
∣
ψ
⟩
=
1
2
n
/
2
Σ
k
=
0
2
n
−
1
e
2
π
i
θ
k
∣
k
⟩
⊗
∣
ψ
⟩
|\psi\rangle=\frac{1}{2^{n/2}}\Sigma_{k=0}^{2^n-1}e^{2πi\theta_k}|k\rangle \otimes |\psi\rangle
∣ψ⟩=2n/21Σk=02n−1e2πiθk∣k⟩⊗∣ψ⟩
根据量子力学的原理,对于一个
n
n
n 量子比特的纠缠态,其总幅值必须是
1
1
1,因此每个基态的系数是
1
2
n
=
1
2
n
/
2
\frac{1}{\sqrt{2^n}} = \frac{1}{2^{n/2}}
2n1=2n/21。因此,在上述公式中,系数为
1
2
n
/
2
\frac{1}{2^{n/2}}
2n/21。在量子相位估计算法中,
k
k
k 表示控制门
U
2
k
U^{2^k}
U2k,其中
U
U
U 是待估计相位的幺正门。我们将
U
U
U 控制在
n
−
k
−
1
n-k-1
n−k−1 个辅助比特上,以获得有关相位
θ
\theta
θ 的
2
n
−
k
−
1
θ
2^{n-k-1}\theta
2n−k−1θ 的估计值。因此,
k
k
k 取值范围为
[
0
,
n
−
1
]
[0, n-1]
[0,n−1]。在量子相位估计算法中,k表示辅助比特测量结果的二进制位数,从0开始编号。当我们对辅助比特进行测量,并将测量结果转换为一个二进制小数时,k表示二进制小数中的小数点后第k位。
然后是量子傅里叶变化的逆:
∣
ψ
⟩
=
1
2
n
Σ
x
Σ
k
e
−
2
π
i
k
(
x
−
2
n
θ
)
2
n
∣
x
⟩
⊗
∣
ψ
⟩
|\psi\rangle=\frac{1}{2^{n}}\Sigma_x\Sigma_{k}e^{\frac{-2πik(x-2^n\theta)}{2^n}}|x\rangle \otimes |\psi\rangle
∣ψ⟩=2n1ΣxΣke2n−2πik(x−2nθ)∣x⟩⊗∣ψ⟩
其中
x
=
2
n
θ
x=2^n\theta
x=2nθ是最有可能的输出。



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










