一、LTI连续系统的响应
1.1连续系统的描述-电路图建立微分方程
主要内容:
1. 数学模型
2. 相似系统
基本要求:
掌握连续电路系统的数学模型
1.数学模型
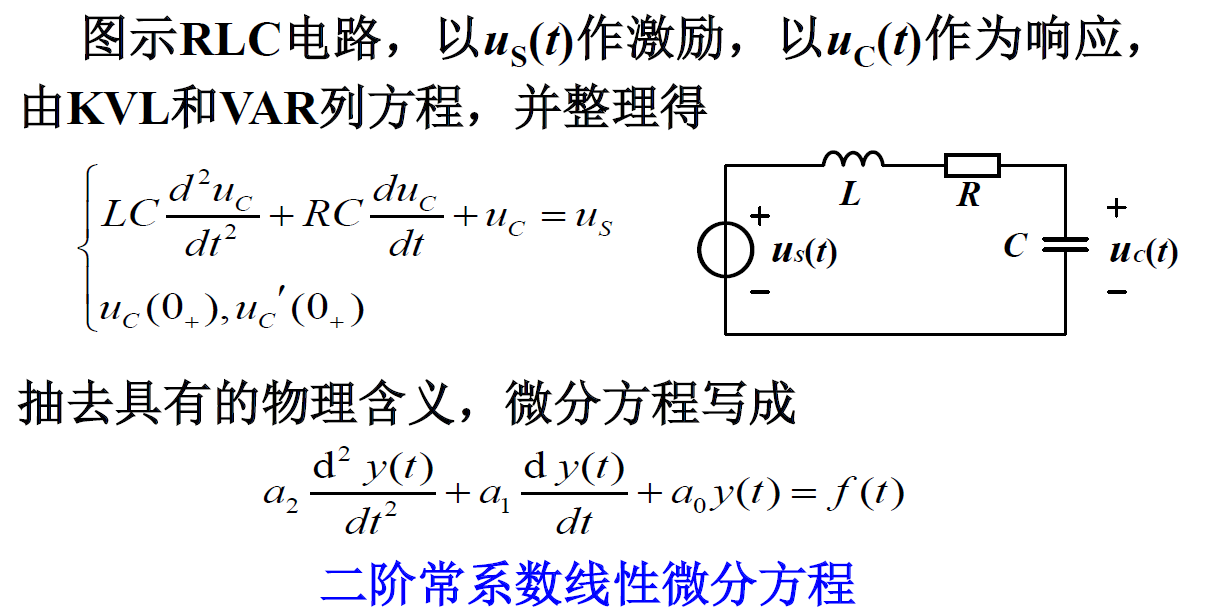
2.相似系统
- 相似系统:能用相同方程描述的系统。

1.2微分方程的模拟框图
主要内容:
1. 基本部件的模型
2. 框图和方程之间的转换
基本要求:
1. 掌握框图的作图方法
2. 熟练掌握框图和微分方程的关系
1.基本部件:
- 基本运算:数乘、微分、相加
- 基本部件:加法器、数乘器、积分器
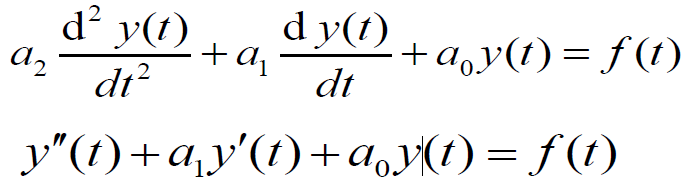
2.模拟框图
- 模拟框图:将微分方程用基本部件的相互联接表征出来的图,简称框图。
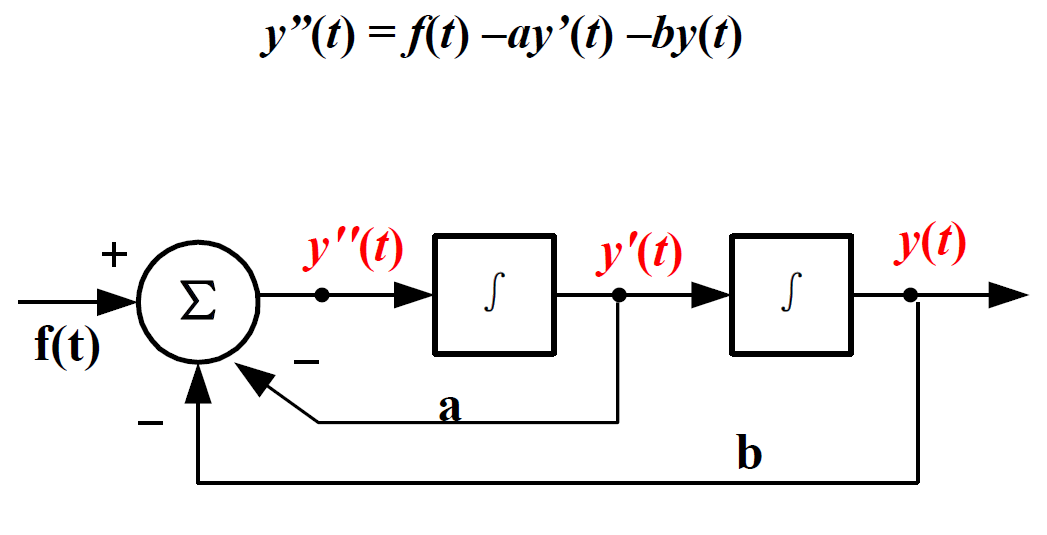
例1 已知y’’(t) + ay’(t)+ by(t) = f(t),画出框图。
解:将方程改写为 y”(t) = f(t) –ay’(t) –by(t)
绘制步骤为:
(1)画出两个积分器;
(2)以最后一个积分器的输出端为y(t);
(3)左边第一个积分器的输入端就是y”(t),也是加法器的输出。
例2 已知y”(t) + 3y’(t)+ 2y(t) = 4f’(t) + f(t),画框图。
解:该方程右端含f(t)的导数,引入辅助函数画出框图。
设辅助函数x(t)满足
x”(t) + 3x’(t)+ 2x(t) = f(t)
移项整理得: x”(t) = -3x’(t)-2x(t) + f(t)
可推导出: y(t) = 4x’(t) + x(t)。(由LTI特性)
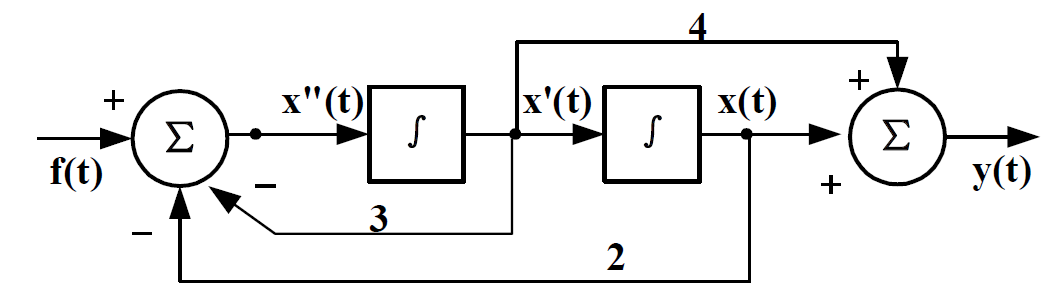
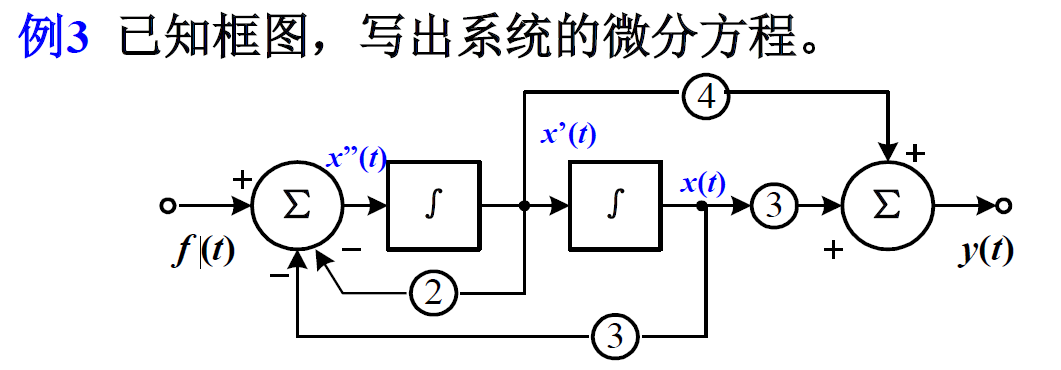
解:设辅助变量x(t)如图
x”(t) = f(t) – 2x’(t) –3x(t)
即 x”(t) + 2x’(t) + 3x(t) = f(t)
y(t) = 4x’(t)+ 3x(t)
根据前面的逆过程,得y”(t) + 2y’(t) + 3y(t) = 4f’(t)+ 3f(t)
1.3微分方程的经典解法
主要内容:
1. 齐次解的定义和解法
2. 特解的含义和全响应的求解
基本要求:
1. 熟悉齐次解和特解的函数形式
2. 掌握微分方程的经典解法
1.经典解

2.齐次解的常用函数形式

3.特解的常用函数形式

例题


1.4系统的初始值
主要内容:
1. 初始值的定义
2. 初始值的求法
基本要求:
1. 了解初始值的概念
2. 掌握系数匹配法
- 初始值是n阶系统在t=0时接入激励,其响应在t=0+时刻的值,即
![]()
- 初始状态是指系统在激励尚未接入的t=0-时刻的响应值y(j)(0-),该值反映了系统的历史情况,而与激励无关。
- 为求解微分方程,需要从已知的
 求得
求得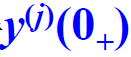
例1
某系统描述某系统的微分方程为y”(t) + 3y’(t) + 2y(t) = 2f’(t) + 6f(t).
![]()
解:将f(t)=ε(t)代入微分方程得
y”(t) + 3y’(t) + 2y(t) = 2δ(t) + 6ε(t)
系数匹配:上式在[0- , 0+]区间两端δ(t)项的系数应相等。
由于等号右端含2δ(t) ,故只有y”(t)包含δ(t)
【这意味着什么呢?
- y''在t=0有冲激变化,且y'和y均无冲激变化
- y'在t=0有阶跃变化,变化幅度看冲激幅度
- y在t=0连续】
故:
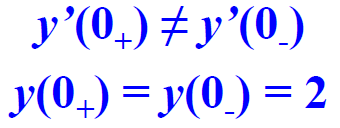

结论:
- 微分方程等号右端含有δ(t)时,仅在等号左端y(t)的最高阶导数中含有δ(t),则y(t)的次高阶跃变,其余连续;(最高阶冲激>>>次高阶跃变>>>其余连续)
- 若右端不含冲激函数,则不会跃变。(无冲亦无跃)
1.5零输入响应
主要内容:
1.零输入响应的初始值
2.零输入响应的求解步骤
基本要求:
1. 了解零输入响应的初始值
2. 掌握求解方法


1.6零状态响应
主要内容:
1. 零状态响应的初始值
2. 全响应的求解
基本要求:
掌握零状态的求解方法
1.初始值的确定
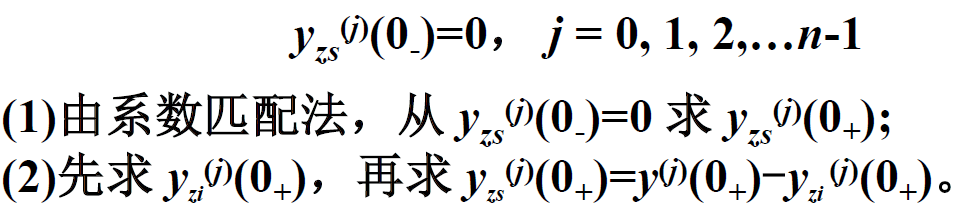
2. 求解步骤
(1)设定齐次解;
(2)设定特解,代入方程求解;
(3)代入初始值,求待定系数。


1.7响应分类
主要内容:
1. 固有响应和强迫响应
2. 暂态响应和稳态响应
基本要求:
掌握响应分类的判定方法
1.7.1. 固有响应和强迫响应
- 固有响应仅与系统本身的特性有关,而与激励的函数形式无关。
- 齐次解的函数形式仅与特征方程的根有关,特征方程的根称为系统的“固有频率”,齐次解常称为系统的固有响应或自由响应。
- 强迫响应与激励的函数形式有关。
- 特解的函数形式与激励的函数形式有关,常称为强迫响应。
1.7.2. 暂态响应和稳态响应
- 暂态响应是指响应中暂时出现的分量,随着时间的增长,它将消失。
- 稳态响应是稳定的分量,若存在,通常表现为阶跃函数和周期函数。比如,电路系统中的直流稳态响应和正弦稳态响应。
例

解: y”(t) + 5y’(t) + 6y(t) = f(t)
其对应特征方程的特征根为-2, -3

小结:
- 全响应中的齐次解部分是固有响应分量,剩余部分是强迫响应。其中,强迫响应在形式上和输入(激励)函数相同。
- 全响应中的各个部分分别进行t取无穷大求极限,若收敛则暂态,反之为稳态。
1.8Maltab求解系统的响应
主要内容:
1. Matlab求解系统响应的函数
2. 系统模型建立的函数
基本要求:
掌握系统响应求解的函数
基本概念
- 求LTI系统的零状态响应的函数lsim,其调用格式为y=lsim(sys, f, t)
- 式中,t表示计算系统响应的抽样点向量;f是系统输入信号,sys是LTI系统模型,用来表示微分方程。
- 系统模型sys要借助tf函数获得,其调用方式为sys=tf(b, a)
- 式中,b和a分别为微分方程的右端和左端各项的系数。
- 比如: y”(t) + 5y’(t) + 6y(t) = f”(t) + 2f(t)
- a=[1, 5, 6]; b=[1, 0, 2]; sys=tf(b, a)
例
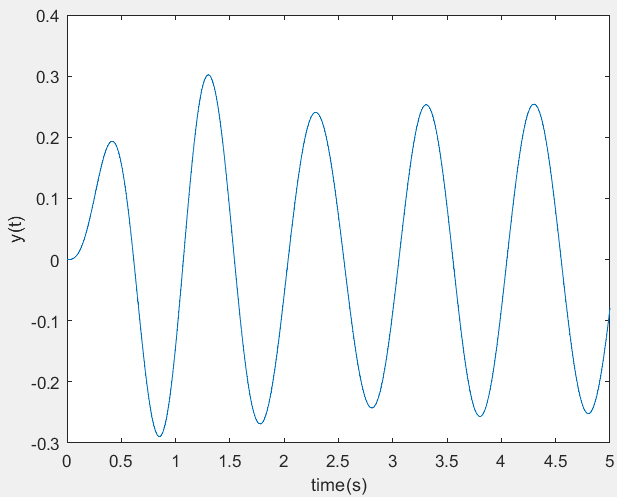
系统的微分方程为y”(t) + 2y’(t) + 77y(t) = f(t),在t≥0接入激励f (t)=10sin(2πt),求零状态响应。
解:b=[1];a=[1 2 77]; f=10sin(2*pi*t);
分别调用sys=tf(b,a)和y=lsim(sys,f,t)可以获得系统模型和零状态响应。
则M语言如下:
b=[1];
a=[1 2 77];
t=0:0.001:5;
f=10*sin(2*pi*t);
sys=tf(b,a);
y=lsim(sys,f,t);
plot(t,y);
xlable('time(sec)');
ylabel(y(t));
二、冲激响应与阶跃响应
2.1冲激响应的定义和求法
主要内容:
1. 冲激响应的定义
2. 冲激响应的求法
基本要求:
1. 掌握冲激响应的定义
2. 掌握冲激响应的求法
2.1.1定义
- 冲激响应是由单位冲激函数δ(t)所引起的零状态响应,记为h(t)。
- h(t)隐含的条件:
- f(t)=δ(t)
- h(0-)=h’(0-)=0 (对二阶系统)
- 基本信号:冲激函数δ(t)
- 基本响应:冲激响应h(t)
2.1.2求法

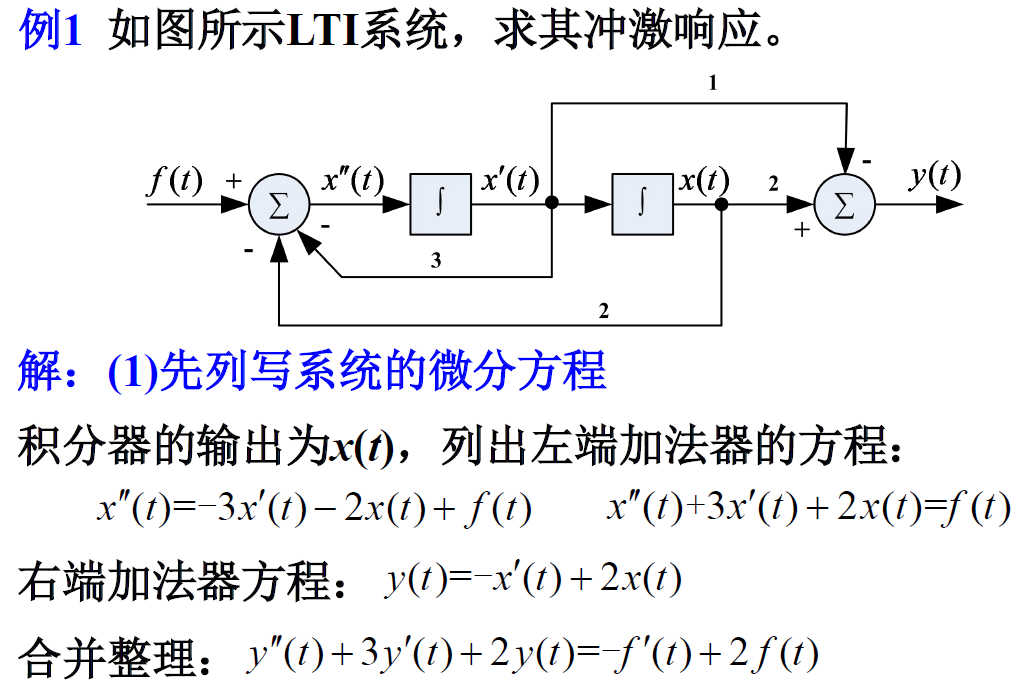


说明:结合零状态响应的线性性质和微分性质,来简化求解过程;若直接进行求解,方程右端将会出现冲激函数的各阶导数。
2.2阶跃响应的定义和求法
主要内容:
1. 阶跃响应的定义
2. 阶跃响应的求法
基本要求:
掌握阶跃响应的求法
2.2.1定义
- 阶跃响应是由单位阶跃函数ε(t)所引起的零状态响应,记为g(t)。
- g(t)隐含的条件:
- f(t) = ε(t)
- g(0-) = g’(0-) = 0
- 基本信号:阶跃函数ε(t)
- 基本响应:阶跃响应g(t)
2.2.2求法


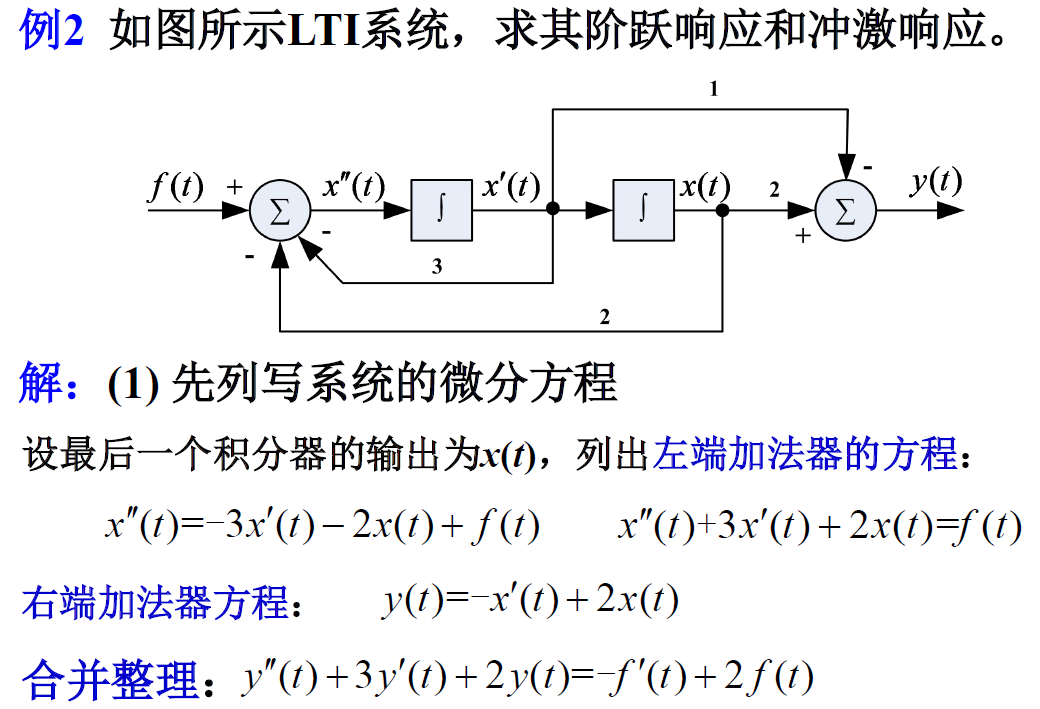


说明:可以灵活运用冲激响应和阶跃响应之间的关系;注意中间变量 g1(t)的表达式。
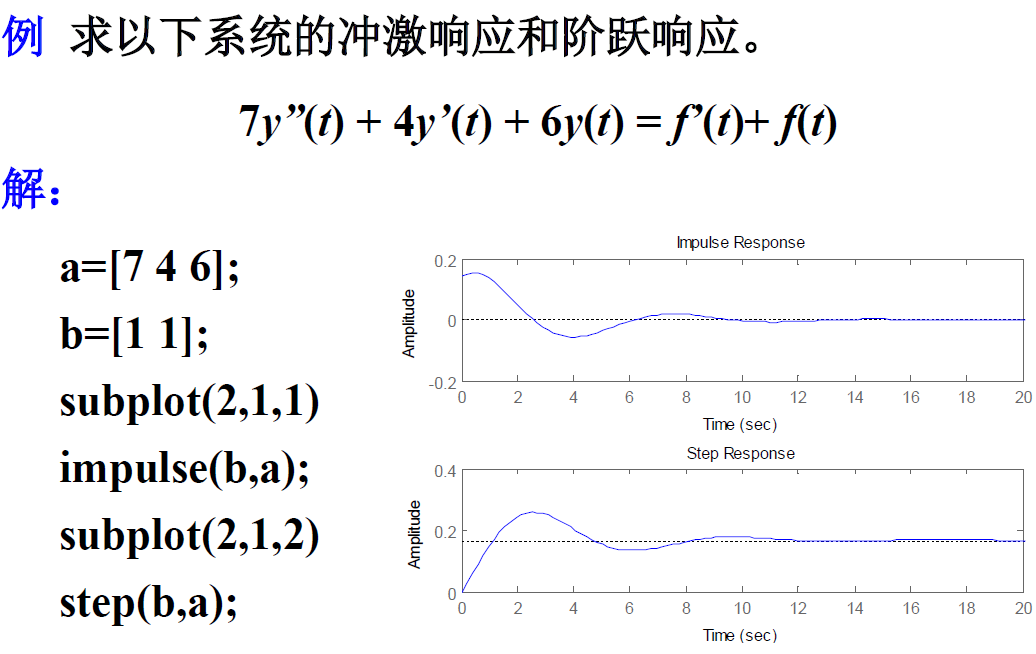
2.3Maltab求解冲激响应和阶跃响应
主要内容:
Matlab求解冲激响应和阶跃响应的函数
基本要求:
了解冲激响应和阶跃响应的Matlab求解方法
2.3.1基本定义


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








