ECML-PKDD ‘25 | FCA-RL框架——基于强化学习的出行服务商动态市场环境效率保障方法

标题：Order Acquisition Under Competitive Pressure: A Rapidly Adaptive Reinforcement Learning Approach for Ride-Hailing Subsidy Strategies

作者：Fangzhou Shi（史方舟）、Xiaopeng Ke（柯晓鹏）、Xinye Xiong（熊薪叶）、Kexin Meng（孟可欣）、Chang Men（门畅）、Zhengdan Zhu（朱正丹）

论文链接：https://arxiv.org/pdf/2507.02244

摘要

网约车平台在为乘客带来更多出行选择和便利的同时，也为出行服务提供商带来了增长机遇。然而，这一机遇也伴随着严峻的挑战：各服务商如何在有限的预算约束下，平衡动态市场竞争与稳定服务供给之间的关系，即既要有效吸引乘客，又能确保服务的价格合理性与可靠性。令人遗憾的是，立足于这一实际业务背景、能够同时保障服务可持续性与乘客利益的相关研究目前尚显不足。

为填补这一空白，我们提出了一种名为FCA-RL的创新型投资优化框架，旨在帮助服务商更高效、更负责任地运用投资资源参与竞争。该方法设计了一种快速竞争适应（FCA） 的机制，使其能敏捷响应动态变化的市场格局（如竞争对手的投资策略调整行为）。同时结合基于强化学习的拉格朗日乘子调整（RLA） 技术，确保在优化决策时严格遵循预算约束，提高每笔投资资金的有效利用率（钱效），最终服务于在有限投入下为乘客争取更佳的综合体验（包括合理价格与可接受的服务可得性）。

此外，我们还开发了一个面向网约车平台的多服务商价格仿真环境RideGym，在不影响实际运营效率的前提下，为不同投资策略提供全面评估与性能基准测试。在RideGym中的实验结果表明，在多种竞争条件下，FCA-RL方法持续优于其他静态的基线方案。

研究背景介绍

近年来，随着网约车行业的发展，整合第三方网约车服务商的打车平台（Ride-hailing Aggregator，RHA）开始兴起。网约车平台为小型出行服务商（Ride Service Provider，RSP）提供更多的流量，不仅提高了乘客出行需求的满足率，还使小型出行服务商（RSP）能够借助平台流量提升他们的订单量和商品交易总额（GMV）。

在我们的业务场景中，核心参与方包括乘客、网约车平台（RHA）和出行服务商（RSP），三者的交互流程如下图所示。为优化乘客体验，RHA通常自动选择报价最低的前K个选项。该机制强烈激励RSP进入此范围，因为多数乘客发送订单时会因操作惯性维持平台默认选择范围。

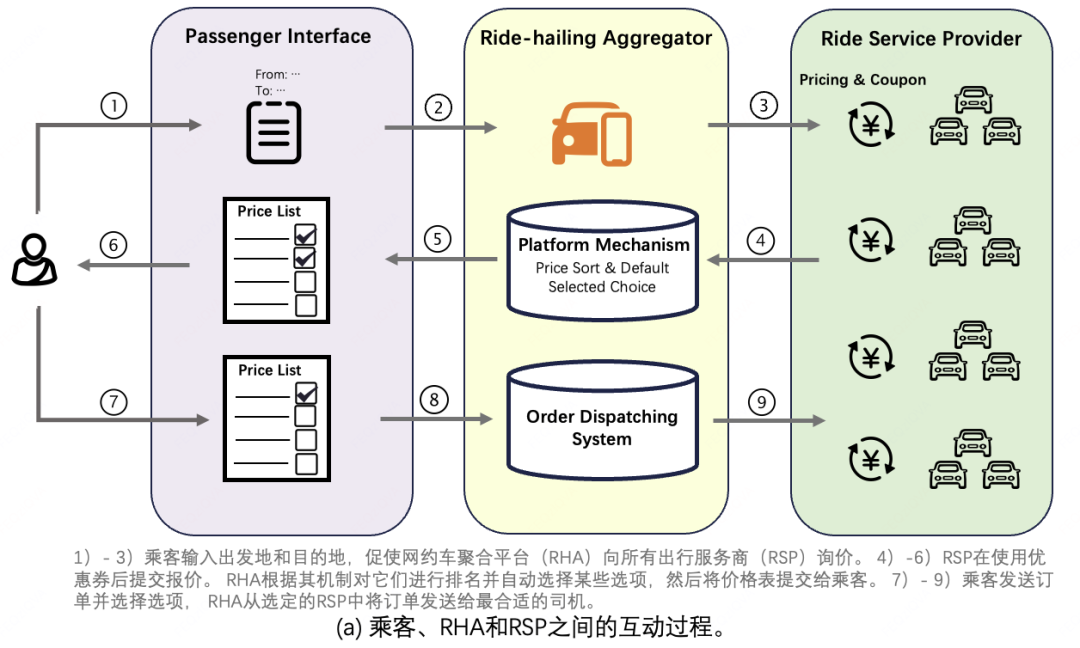
订单发送后，系统会将其调度给乘客所选的RSP中最合适的司机，这意味着对一个RSP而言，乘客单次请求中选择的服务商选项越少，其面临的竞争越小。因此，与其他RSP进行出行费用的竞争，本质上是通过促使乘客勾选自己并发送订单，从而提高订单量。不同于之前众多讨论城市长期基础定价策略或极端供需条件下动态调价的研究，本文主要讨论承担供需调节作用的即时投资策略，并且聚焦在一个尚未被充分探索过的研究场景——在RHA中，作为RSP如何通过精细化的动态调节投资策略来快速响应市场的竞争。

三个核心贡献：

首个聚焦于RSP的投资策略的研究：据我们所知，这是首次从RSP视角出发，探索并实现调整投资策略来即时应对市场环境变化的研究。

新型动态RL投资框架：提出FCA-RL框架，集成快速市场响应模块，在动态市场中实现精准预算控制而不影响投资效能。

全链路网约车平台模拟器：开发RideGym系统，建模网约车内订单全生命周期，支持多算法与环境变量下的投资策略综合分析。

问题定义

核心问题定义 

目标：出行服务商（RSP）在网约车平台（RHA）中，通过动态优化即时投资策略实现：

• 最大化订单完成量。

• 满足预算约束：总投资支出 ≤ 总GMV × 预算率 B。

关键挑战

• 竞争性敏感：RHA自动选择前K个最低报价，RSP需通过折扣券以进入RHA的默勾范围。

• 预算硬约束：投资成本需严格控制在GMV的固定比例内。

• 数据分布漂移：竞争对手不定期投资幅度变化导致我方IRR动态变化。

注：IRR为In-Range Rate，表示我方RSP进入默勾范围的概率，后文中提到IRR分布变化可整体理解为一个分布集合的变化，集合中包括每种候选折扣下我方RSP进入RHA默勾范围的概率分布。

静态数学模型构建 

原始优化问题

定义决策变量：

   :是否对订单i应用折扣券  （one-hot编码）。

  :应用折扣券  后订单 i的完成概率估计。

约束优化形式：

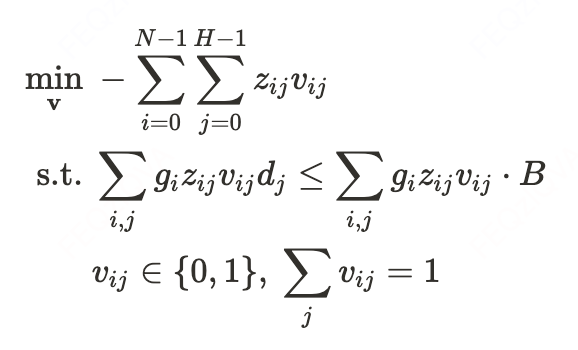
物理意义：最小化未完成订单数（等价于最大化完成量），同时满足投资成本率 ≤ B。

拉格朗日对偶变换

为高效求解，我们对变量  的整数约束进行线性松弛，并利用其强对偶性在对偶空间进行求解，引入拉格朗日乘子 λ≥0转化为无约束的优化问题：

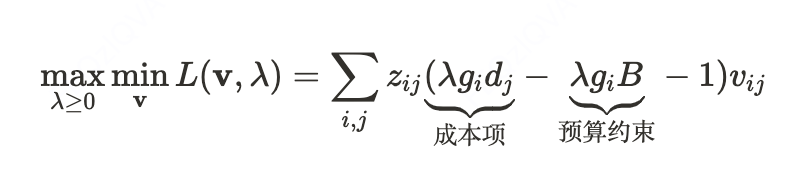
针对这个问题，我们可以对  和  进行交替最优求解：

• 固定 λ 时，最优折扣券选择为：

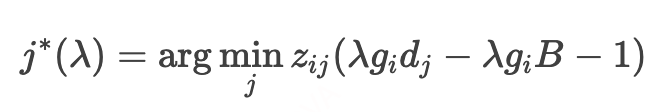
• 不难看出，关于  的函数为分段线性的凸函数（Piece-wise Linear），考虑其存在不可微点，我们选择通过三分查找法来求解最优  ，伪代码如下：

def ternery_search():    l, r = start, end    epsilon = 1e-5    while l + epsilon < r:        one_third_point = (r - l) / 3.0        mid_1 = l + one_third_point        mid_2 = mid_1 + one_third_point        if f(mid_1) <= f(mid_2):            r = mid_2        else:            l = mid_1    return l

动态市场环境下的挑战

在我们的背景设定下，站在我方RSP视角，其他RSP不定期投资幅度变化会导致市场环境动态变化，这会导致在原问题下的求解出的最优解在后续竞争的过程中发生偏移，使得最终花费偏离最初的预算约束，以及原始最优解的钱效变低。

静态最优解失效原因

一个订单的完单率可以解藕为：

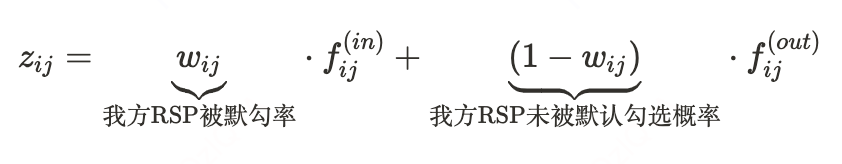
•    ：我方RSP应用折扣券  后进入前K名的概率。注意，这是对其他RSP的投资幅度变动最敏感的部分。

•   ：我方RSP进入默勾范围情况下的订单完成概率。进入默勾范围后，完单概率更多受到RSP运力情况影响。

•   ：我方RSP未进入默勾范围情况下的订单完成概率（假设正常情况下乘客加勾更高价格的意愿较低，通常接近于0）。

假设原始最优解  是通过  时段区间的数据求解获得，而在未来  的时段，其他RSP又发生投资策略变化，这使得：

=> RHA表单中，我方RSP的排序分布发生变化，  。

=> 我方RSP的IRR分布发生剧烈漂移。

=> 静态优化解  失效，即  。

因此，我们需要对市场环境变化导致的我方IRR变化进行显式地动态建模和跟踪。除此之外，为了及时调整我方RSP的投资策略来适配市场环境的变化，我们将整个问题建模成马尔可夫决策过程，通过强化学习进行时间片粒度的最优解调整，来保证我方RSP的投资策略在市场动态变化下的钱效。

FCA-RL方法框架

为了解决上述问题，我们提出了一个基于强化学习的投资策略框架FCA-RL（见图2）。首先我们将整个动态决策过程建模成马尔可夫决策过程（Marcov Decision Process，MDP），并通过强化学习的策略网络对静态建模中的最优拉格朗日乘子进行调整（Reinforced Lagrangian Adjustment，RLA）。注意，在每个决策时间步t的状态表征中，我们会考虑当前时间步的IRR变化，我们提出通过一个快速适配IRR分布变化的模块（Fast Competition Adaption， FCA）来及时跟踪并记录我方RSP的变化。

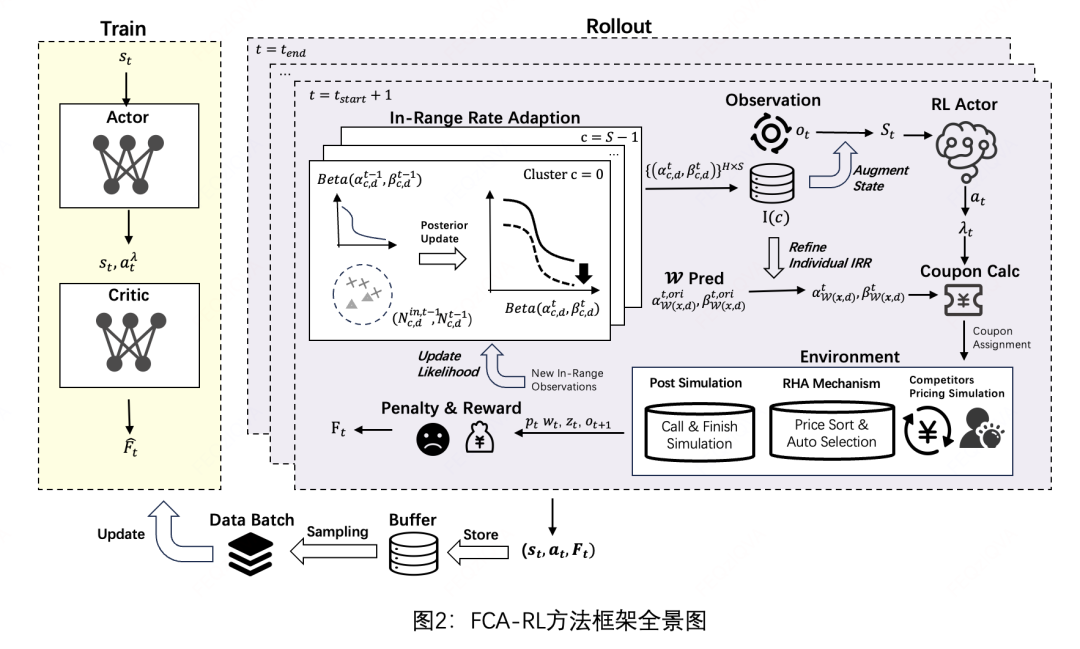
基于强化学习的拉格朗日乘子调整

核心思想：将拉格朗日乘子λ的动态优化建模为马尔可夫决策过程（MDP），实现预算约束下的动态实时决策调整。

马尔可夫决策过程（MDP）建模

我们将带约束的λ动态调整过程定义为六元组  ：

强化学习拉格朗日乘子调整

本工作采用Actor-Critic框架。在每个时间步长t中，策略网络  （由θ参数化）作为神经网络接收当前状态作为输入，并输出高斯分布的均值  和标准差  。随后从该分布中采样生成动作  。该动作通过下面公式调整前一时刻的拉格朗日乘子  。  对  的作用机制如下（lb为限定下界，ub为限定上界）：

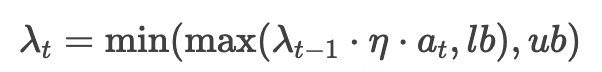
注意，为了保证  的更新更加平滑稳定，我们会在更新后的  上进行再度调节：

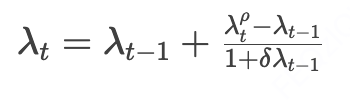
其中  表示上次变化量，  代表  由初步修正的λ值。调整后的  代入下述公式，确定当前时段各请求的最优折扣券分配方案。

每个时间步的折扣券最优决策公式（推导请参照前面的静态数学模型构建）为：

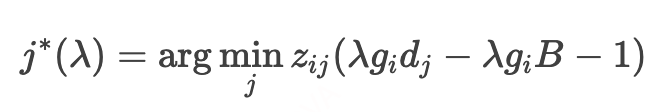
评估网络  则基于状态-动作对  预估成就值  。评估网络训练为MSE loss，策略网络则选用PPO的损失函数进行训练（详见Algorithm 1）。

快速竞争适应

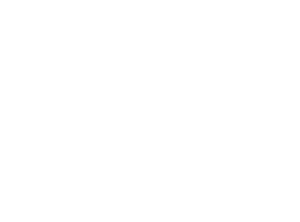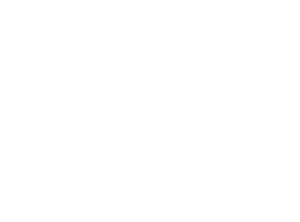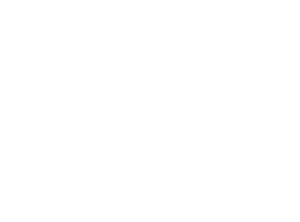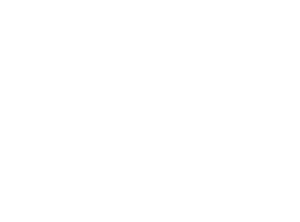
IRR初始Beta分布建模 

在每一时间步t，为即时响应竞争对手偶发性投资幅度调整引发的我方IRR波动，我们提出将各候选折扣券的初始IRR分布态势建模为一组Beta分布，并且借助Beta-二项分布的共轭性，通过贝叶斯后验更新动态，实现对分布变化的快速追踪。我们可以证明，当满足假设1时，命题1成立，为对初始IRR分布的建模为Beta分布的合理性提供了理论保证。

假设 1（RSP同质性假设）：

所有出行服务提供商（RSP）均属同一服务类别（如经济型）。当其加入网约车平台（RHA）时，针对特征相同的请求 x，各RSP的报价   服从独立同分布的连续分布，其累积分布函数（CDF）为  。

命题 1：

设给定请求i对应的RSP数量为 M。排在第  低的报价的累积分布函数  服从Beta分布（证明见论文附录D）。由此可直接推导，对于初始时刻 t=0的用户请求i，我方的IRR服从：

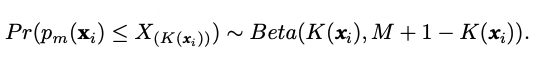
下文阐述如何利用Beta-二项分布的共轭特性，实现在每个时间步上进行贝叶斯后验更新，从而快速地适应前一时刻竞争对手的投资策略变化。

Beta分布后验更新 

特征聚类

对个体样本粒度的IRR Beta分布进行追踪所面临的核心挑战在于不同时间步的样本并不同质，因此t-1时刻观测到的进入默勾范围的结果无法直接应用于 t时刻的个体样本。为此，我们先通过K-Means算法对特征相似的样本进行聚类，构建从特征空间到聚类标签的映射：

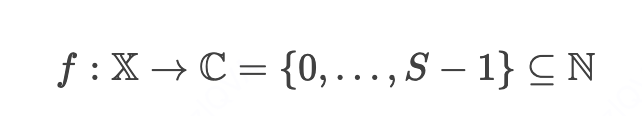
基于此，在可接受的精度损失范围下，我们假设同一类别内的样本具有同质性，因此可以利用第t−1时刻内在每个类别内观测到的我方RSP的被默勾数（服从二项分布），在第t时刻执行贝叶斯后验更新。对每个类别c和折扣券d∈d，记其最新Beta分布参数为  和  。

IRR先验初始化

我们在时间步  启动IRR分布追踪，首先通过一个预训练模型  对一个先验数据集   中的样本在各折扣下的IRR进行Beta分布参数预测，之后按预设的类别和折扣计算Beta分布参数预测值的平均值，生成各聚类c和折扣d的Beta分布初始参数   和  ，这些初始参数会被存储到一个字典中【以聚类中心为键，对应的beta分布参数元组(  ,  )为值】，实现IRR分布初始化。

贝叶斯后验更新

令  表示在 t−1时刻类别c中接受折扣d的样本数，  为其中我方RSP进入默勾范围的样本数。根据Beta-二项分布的共轭性，在t时刻的IRR后验分布仍服从Beta分布（证明见附录E）。参数更新公式为：

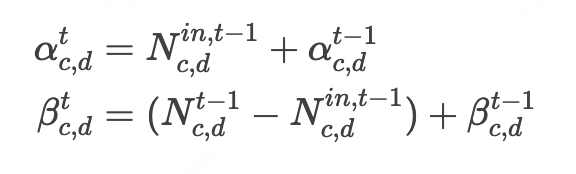
为缓解因单时间步内样本有限导致的Beta分布更新随机噪声，我们引入窗口尺寸参数  ，每次统计前  个时间步的我方RSP的被默勾数（当   =1时则与上述公式一致）。

FCA和RLA的交互

这部分主要介绍如何将FCA模块嵌入到强化学习拉格朗日乘子调节（RLA）的算法流程中，主要分成三个阶段：

  的IRR状态特征更新 

在将t时刻状态输入给Actor之前，我们会对  进行IRR的整体状态更新：两个维的向量，分别包含每个类别的Beta分布参数的对所有候选折扣的均值和 ，其中 , ，这使得Actor可以根据当前的IRR状态来输出动作，通过公式9、公式10进行  调节。

  的更新（样本-折扣粒度）

注意，当IRR分布发生变化时，折扣决策公式（公式11）中的  也会发生变化（根据公式4中对 的拆解，其中 会随其他RSP的行为而发生显著变化，和 则可假设分布不变），因此，我们需要结合字典 对IRR分布的当前最新记录对公式中的 进行更新。初始 的分布参数由预训练模型预测得出（记为 和  ），其参数的后验更新方式如下：

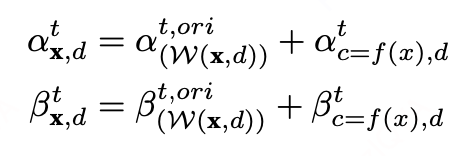
更新t时间步内的所有样本在所有候选折扣下的  之后，即可按照公式11给出t时间步内的所有样本折扣决策。

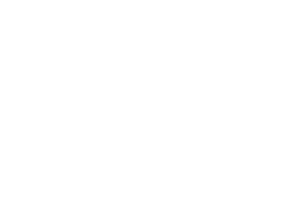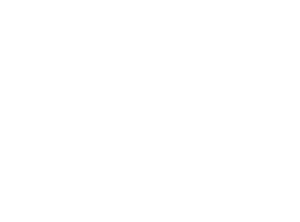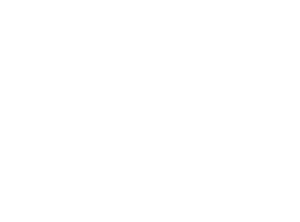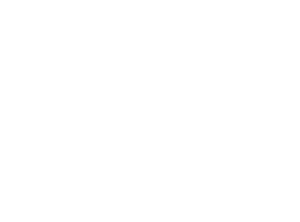
字典  的更新（t时刻的默勾样本数观测）

完成t时间步的折扣决策后，RideGym会对每个样本返回我方RSP是否进入默勾范围的结果，需要统计此时每个类别的  以及  ，对字典  的值进行更新。

整个FCA-RL的算法流程如下：

RideGym

为规避在线环境直接部署新投资策略造成的资损风险，我们提出RideGym离线仿真系统——该系统对网约车平台（RHA）的完整订单生命周期流程进行建模。如图3所示，RideGym由三大核心组件构成：基础定价引擎（Basic Pricing Engine）、投资策略引擎（Strategy Engine）和 后定价引擎（Post-Pricing Engine）。该框架支持在不同市场条件下评估各类投资策略，且无需承担实际部署的潜在损失。这套离线仿真系统将在后续开源，敬请关注。

基础定价引擎

报价生成机制

每笔订单的基准价格通过可配置的里程单价确定。

出价模型

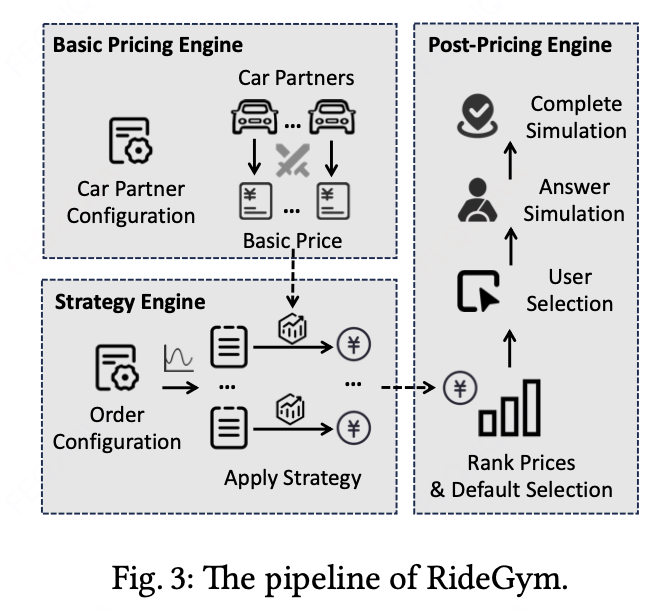
单一RSP的投资策略变化将影响平台内其他服务商。为模拟市场竞争的不确定性，我们引入随机投资机制：

其中投资幅度a从预设边界  定义的均匀分布中采样。

策略引擎 

订单流生成

采用混合正态分布逼近实际订单分布，按时间步生成订单并维持目标订单量分布。

投资策略配置

各RSP可应用自定义的投资策略，为订单分配折扣。

后定价引擎 

服务商排序与默勾机制

• 处理所有RSP的报价，按升序排列。

• 模拟平台自动选择（RHA Top-K机制）与乘客手动选择。

乘客选择建模

设 M个RSP的报价序列为  ，乘客实际选择的RSP数量 K′由下式计算：

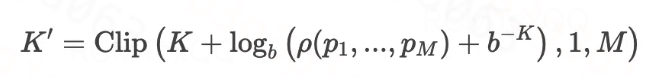
其中：

• K：RHA默认选择的RSP数量。

• b：可调基数（b>1）。

• ρ(⋅)：价格序列密度函数。

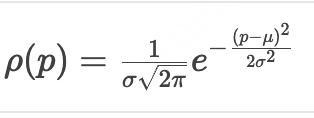• Clip(x,l,u)：将勾选RSP数截断在 [l,u]区间。

司机响应建模

为每笔订单分配随机供应因子 s∼U[0,1]，设M个RSP的服务能力 (运力数) 分别为   ，第i个RSP接单概率为：

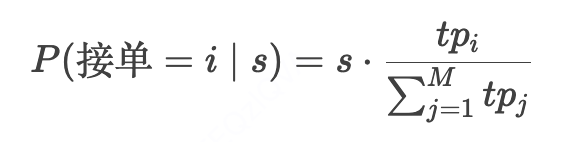
订单无响应概率：

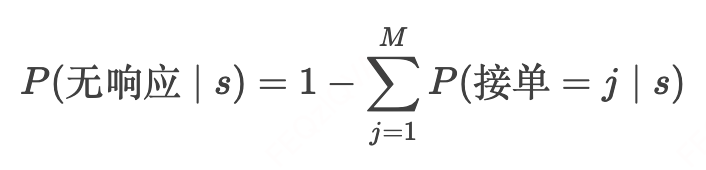
订单取消模拟

通过正态分布  建模每个订单、每个RSP司机或乘客的潜在取消行为。

实验评估

实验设置 

数据集配置

在RideGym平台上生成四种差异化场景（标记为Scene-1至Scene-4），各场景包含三组数据集：

• 预训练集（Pre-train）：模型初始化数据，含168个时间片（每个时间片为1小时），Scene-4。

• 训练集（Train）：策略优化数据，含720个时间片，Scene-2。

• 测试集（Test）：最终评估数据，含336个时间片，Scene-1～Scene-4。

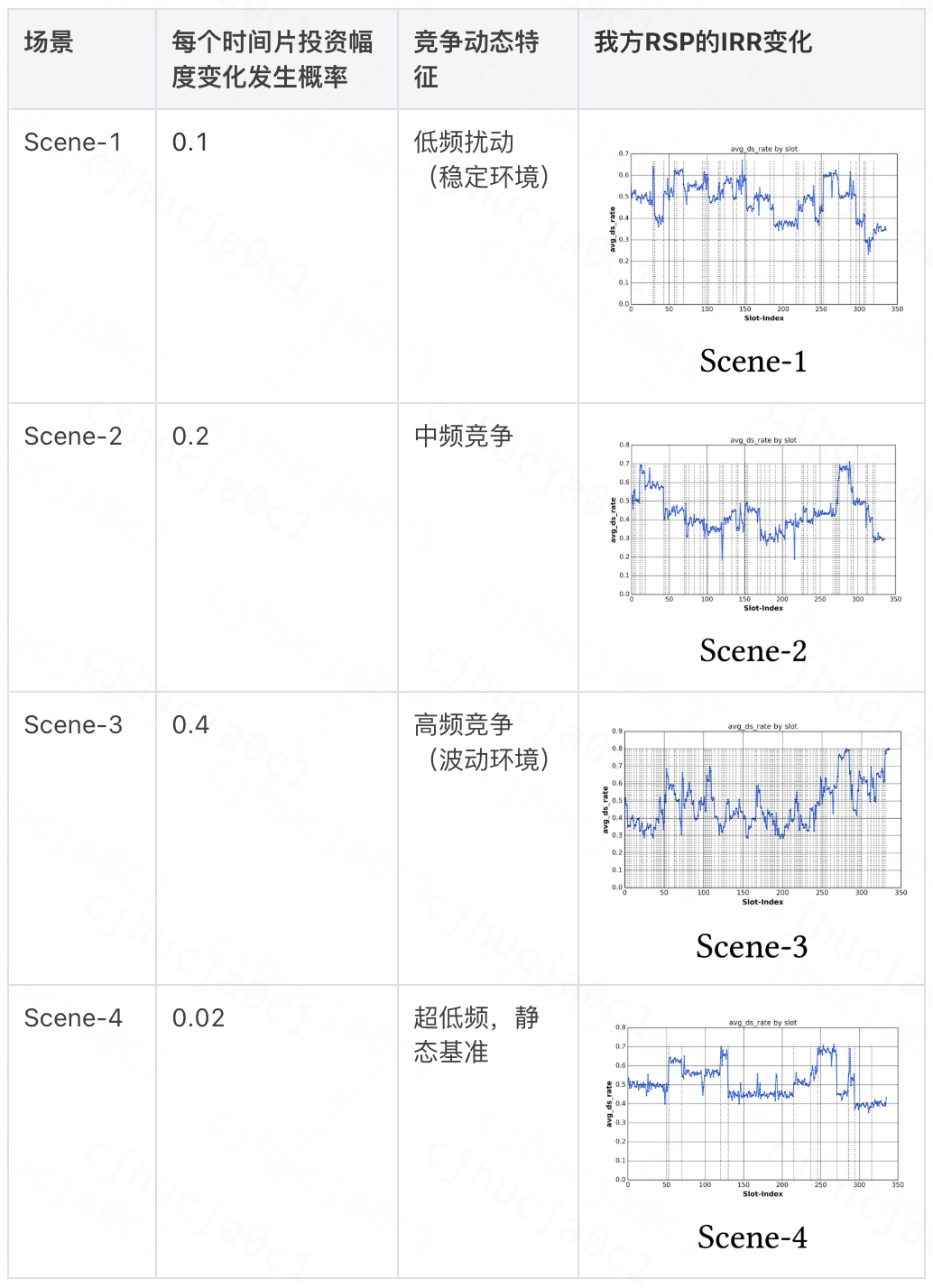
注：Scene-1至Scene-3中竞争对手通过模拟投资幅度变化影响RSP的IRR；Scene-4用于评估静态环境下的算法鲁棒性（详细配置见附录B）。

基线方法

由于之前并没有相关工作研究在RHA的设定中RSP视角下的动态竞争投资策略，因此我们选择两种传统基于静态模型预测+运筹优化的方法（PDM-A和PDM-S）和真实最优策略（OPT）作为基准和我们的算法（FCA-RL）在RideGym产生的数据上进行对比。

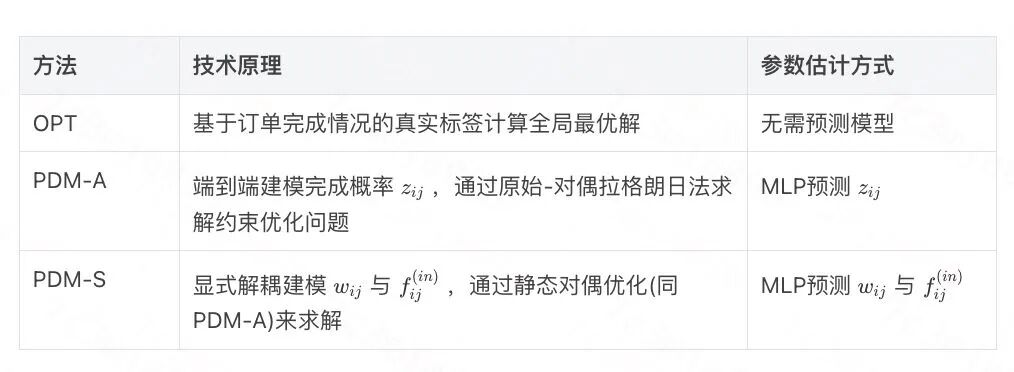
基线PDM-A和PDM-S在相同训练集上求解，测试阶段策略固定不变。OPT则直接在测试集上求解最优解。

评估指标

成本率误差（Cost Rate Error, CRE）

• 衡量预算控制精度（值越小越好）。

• 标注：↑表示超支，↓表示节支。

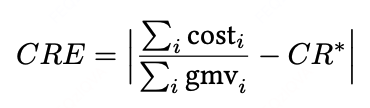
订单完成投资回报（Finish Return on Investment, FROI）

•   ：实施/未实施投资策略的订单完成量。

• C：总投资成本。

•   ：实施/未实施投资策略的客单价（ASP）。

• 反映投资的订单增量效率（值越大越好）。

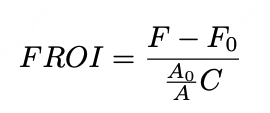
强化学习奖励（Reinforcement Learning Reward, RLR）

•   ：OPT所得的最优订单完成量。

• 综合量化订单增长与投资花费相较目标预算率的差距（值越大越好）。

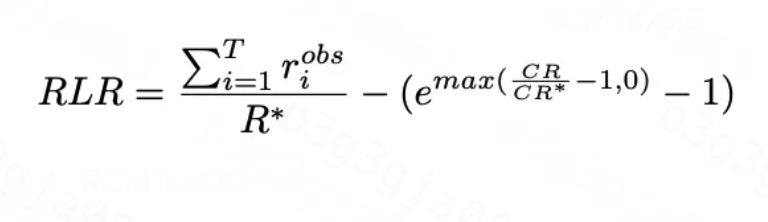
实验效果

我们的实验设计主要为了回答三个问题：

RQ1: FCA-RL和其他基线方法的在不同竞争程度的场景的效果对比如何？

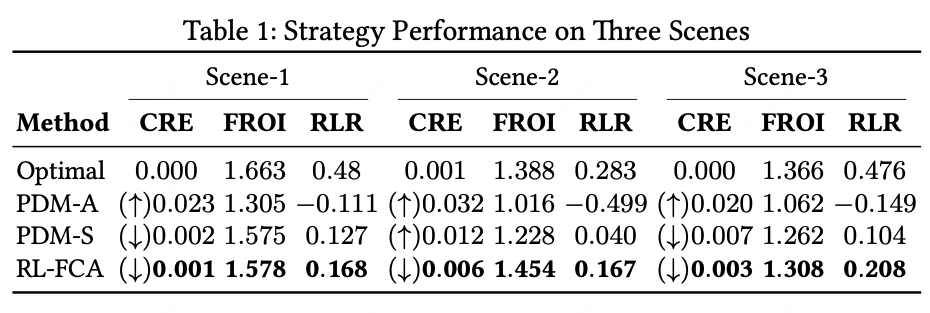
我们在Scene-1至Scene-3场景下评估所有基线方法。结果显示：FCA-RL全面超越基线，其预算控制误差显著降低（Scene-2/3场景误差≤0.3pp，较次优方法PDM-S降低0.4-0.6pp）；值的一提的是，在Scene-3中，FCA-RL在相较于PDM-S成本多花0.4pp的情况下，依然实现了3.6%的FROI提升（从1.262升至1.308）。

RQ2: 其中的FCA模块是否有效？在什么场景下有效？

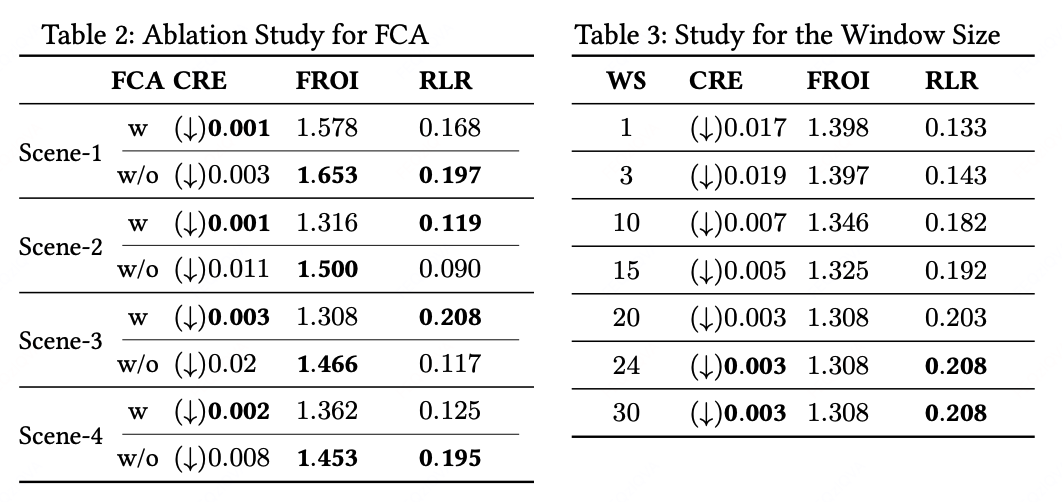
我们在Scene-1至Scene-4场景下对FCA模块进行了消融实验（表2），并在高竞争场景Scene-3分析FCA窗口尺寸的影响（表3）。结果表明：FCA模块在所有场景均降低预算执行误差，在竞争更为激烈的环境（Scene-2/3）中RLR指标较无IRR适应的标准RL提升32.2%和77.4%；但在对手策略较稳定的Scene-1/4场景无显著增益，因在固定分布中实施FCA模块会造成噪声波动，抑制RL收敛效率。窗口尺寸测试揭示：窗口长度≥20时RL训练效果显著提升（表3），长度增至24后性能趋于稳定，故我们的实验最终选定窗口长度为24。

RQ3: FCA-RL是如何超越其他静态基线方法的？如何解释FCA-RL方法的优势？

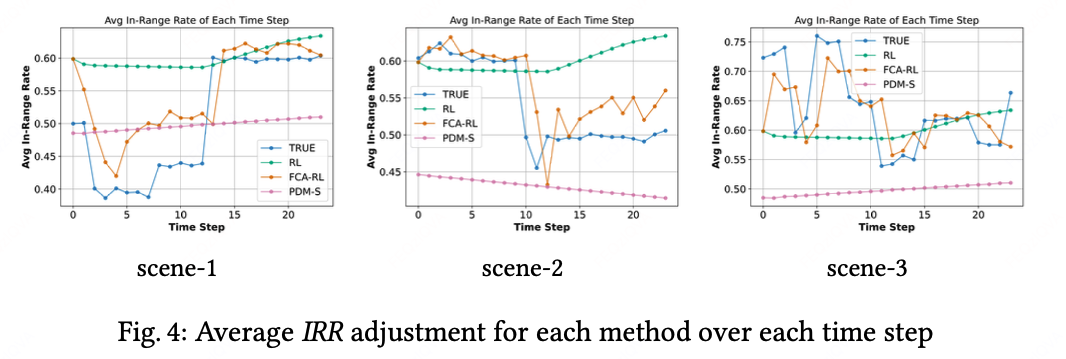
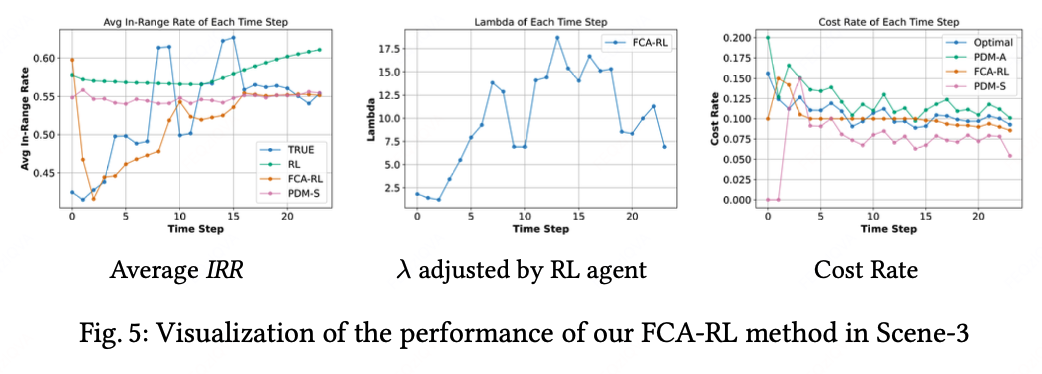
FCA-RL方法通过实时调整拉格朗日乘子（λ）来动态响应市场变化。如图4所示，在其他RSP投资幅度变化引发的IRR分布漂移中，本方法相较依赖训练集分布做静态规划求解的基准方案（PDM-S）展现出更敏捷的适应能力（窗口尺寸为1时，FCA对IRR变化敏感性增强，但会导致RL训练波动加剧）。图5进一步揭示：RL智能体依据IRR分布变化逐步调整λ参数（前两列），第三列对比显示FCA-RL通过实时优化λ，实现相较基线方法有更平滑的预算执行轨迹，并且更严格地控制了预算执行。

结语

我们的方法（FCA-RL）相较于传统基线方法大幅降低了出行服务商在动态市场环境下的投资预算控制误差且提升了订单的获取效率，但依然存有局限，比如暂未考虑建模乘客对于投资的长期心智变化及长期供需变化，在未来的工作中，将会尝试将这些考虑进来。感谢诸位的耐心阅读，欢迎对本文中方法有任何问题和建议的同学联系第一作者进行讨论交流（arkshifangzhou@didiglobal.com）。

团队介绍

花小猪策略部负责国内网约车市场中的智能投资、服务推荐、供需预测、派单、调度等核心算法落地，应用深度学习、强化学习、LLM等提升平台效率与服务体验，以算法创新助力业务增长与发展。 

长期招聘算法实习生，欢迎投递简历至hxz_strategy@didiglobal.com，期待一起让出行更美好！