【动态规划法】-【0-1背包问题】

动态规划法

【动态规划法】于【分治法】非常像，都是将待求解问题分解成若干个子问题。它们的区别是：

【分治法】分解得到的子问题，彼此之间是独立的。
【动态规划法】分解得到的子问题，彼此之间不是独立的，是有关系的。

思路：
保存已解决的子问题的答案，在需要时再找出已求得的答案，这样就可以避免大量的重复计算。
为了达到这个目的，可以用一个表来记录所有已解决的子问题的答案——不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表中。
这就是动态规划法的基本思路。

【动态规划法】适合用于【寻找最优解（最大值或最小值）】类型的问题。

【动态规划法】的基本思想：

什么时候可以应用【动态规划法】来设计算法？
（1）最优子结构
（2）重叠子问题

什么时候可以应用【贪心法】来设计算法？
（1）最优子结构
（2）贪心选择性质

0-1背包问题

题目背景：

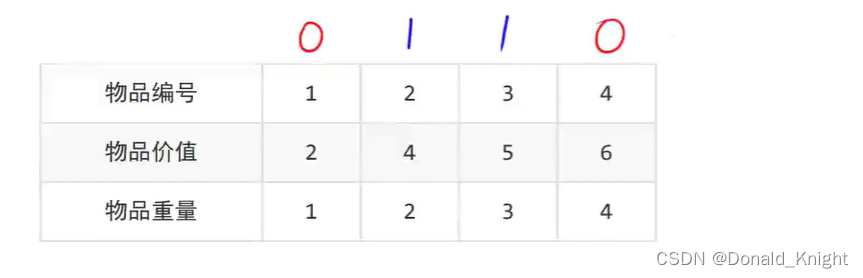
有n个物品，第i个物品价值为vi，重量为wi。有一个背包，背包的容量为W。
（vi，wi，W均为非负数）
现在需要考虑如何选择装入背包的物品，使装入背包的物品总价值最大？

（0-1的意思是：物品要么放入背包，要么不放入背包。1表示放入，0表示不放入。）

假设：
物品数量=4 N
背包容量=5 W

每个物品有各自不同的价值和重量。那么，如何向背包中装入物品，使得背包中物品的总价值达到最大？

如果选择首先把价值最大的4号物品放入背包的话，则为【贪心算法】。【贪心算法】最后得到的结果是：放入1号4号物品，总价值为8。
然而，这只是一个近似最优解，而不是真正的最优解。真正的最优解是：放入2号3号物品，总价值为9。
通过【动态规划法】，可以得到真正的最优解。

解题思想：

0-1的意思是：物品要么放入背包，要么不放入背包。1表示放入，0表示不放入。

例如，放入背包的是2号3号物品，则表示如下图。

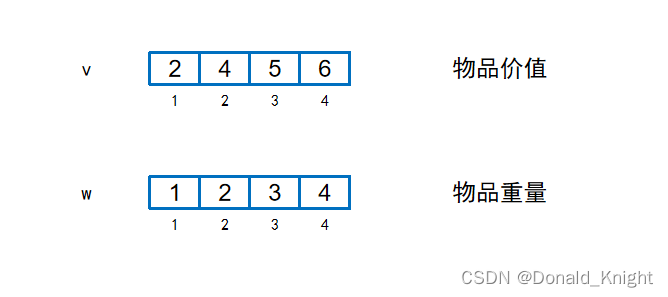
物品价值我们用一个数组 v[ ] 来表示：

物品重量我们用一个数组 w[ ] 来表示：

核心思想：将原问题分解成若干个子问题——如何分解呢？

原问题：从4（N=4）个物品中选择其中几个放入背包，要求总重量不超过5（W=5）。求出这种情况的最大价值为9。

分解成一个范围稍小一点的子问题

子问题：从4（N=4）个物品中选择其中几个放入背包，要求总重量不超过4（W=4）。求出这种情况的最大价值为7。

再分解成一个范围稍小一点的子问题

子问题：从4（N=4）个物品中选择其中几个放入背包，要求总重量不超过3（W=3）。求出这种情况的最大价值为6。

再分解成一个范围稍小一点的子问题

子问题：从4（N=4）个物品中选择其中几个放入背包，要求总重量不超过2（W=2）。求出这种情况的最大价值为4。

再分解成一个范围稍小一点的子问题

子问题：从4（N=4）个物品中选择其中几个放入背包，要求总重量不超过1（W=1）。求出这种情况的最大价值为2。

其中，W=0是一个边界。（这时总价值恒等于0）

同理，N也是可以从4到1逐步缩小范围的。
N的含义是只能从前N个物品中选择。例如当N=3时，我们不可以选择编号4的物品。

其中，N=0是一个边界。（这时总价值恒等于0）

因此，在我们的分析中：
N的取值范围为0~4
W的取值范围为0~5

我们用一个二维数组f来表示所有的这些子问题的情况，数组中每个位置f[i][j]存储该子问题情况下的最优解。

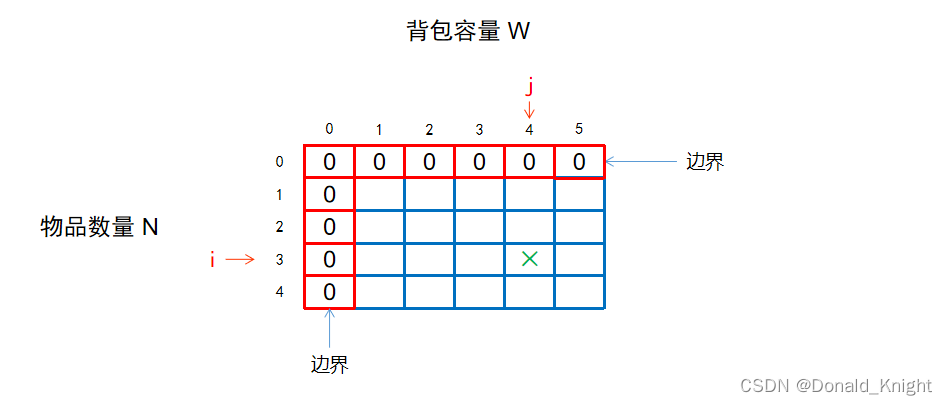
数组中每个位置f[i][j]存储该子问题情况下的最优解。其中，
行数 i 表示物品数量N，
列数 j 表示背包容量W。
上图中绿色的×位置，即f[3][4]，表示N=3，W=4时的情况。该位置存储的是这种情况下的最大价值（即从前3个物品中选，总重量不能超过4的情况）。

图中的最右下角f[4][5]（N=4，W=5）就是我们的原问题的解。为了求出它，我们需要依次求出前边的每个子问题的解。

思想：
把“从前 i 个物品中选”拆成两种情况：
（1）不选中第 i 个物品的情况，求出此情况下的最大价值，记作 a；
（2）选中第 i 个物品的情况，求出此情况下的最大价值，记作 b；（注意要先判断第 i 个物品是否可选——重量是否超过背包）
取两者的最大值——max(a,b)即为我们要的最终答案。

再具体分析下这两种情况：

（1）不选中第 i 个物品的情况：
等于【从前 (i-1) 个物品中选，背包容量为 j 时的最大价值】
此时，f[i][j] = f[i-1][j]

（2）选中第 i 个物品的情况：
前提条件：背包容量j >= 第i个物品的重量w[i]，即 if( j>=w[i] ) 为真，才可以选
等于【第i个物品的价值】+【从前 (i-1) 个物品中选，背包容量为 (j-第i个物品的重量) 时的最大价值】
此时，f[i][j] = v[i] + f[i-1][j-w[i]]

从头开始分析所有的情况：

当 i=0（物品数量为0）时，最大价值一定等于0。
当 j=0（背包容量为0）时，最大价值一定等于0。
因此我们可以先把边界确定下来。

当 i=1，j=1时，表示：从前1个物品中选，总重量不超过1。
此时拆成两种情况：
（1）不选中第1个物品，此情况下的最大价值为0；
（2）选中第1个物品，此情况下的最大价值为2；
因此，最大价值解为max(0,2)=2

f[1][1] = max(0,2) = max(不选中第1个物品的情况, 选中第1个物品的情况)
f[1][1] = max(0,2) = max(f[0][1], (v[1]+f[0][0]))
即
f[i][j] = max( f[i-1][j], (v[i]+f[i-1][j-w[i]]) )

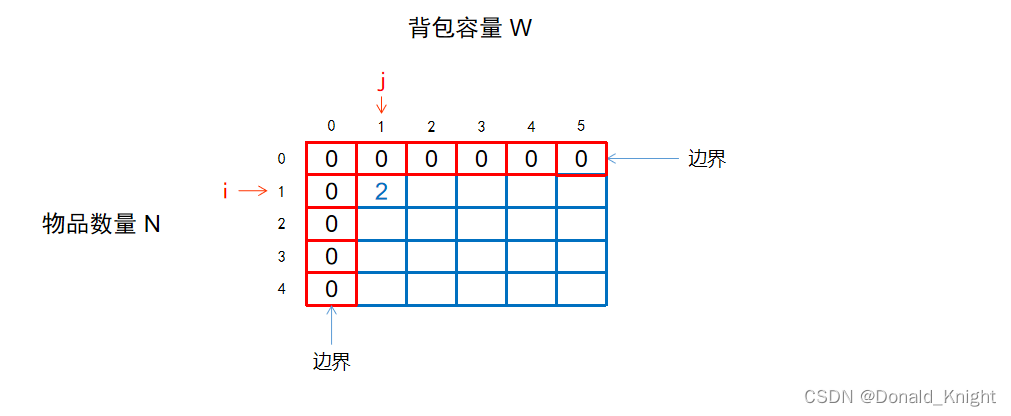
得出f[1][1]的值后，我们让 j++，接着计算f[1][2]

当 i=1，j=2时，表示：从前1个物品中选，总重量不超过2。
此时拆成两种情况：
（1）不选中第1个物品，此情况下的最大价值为0；
（2）选中第1个物品，此情况下的最大价值为2；
因此，最大价值解为max(0,2)=2

到这里可知，当i=1时，表示只有第一个物品。无论背包容量 j 再怎么变大，最大价值都不会有变化了，就是第一个物品的价值。

至此可得出第一行的所有结果。

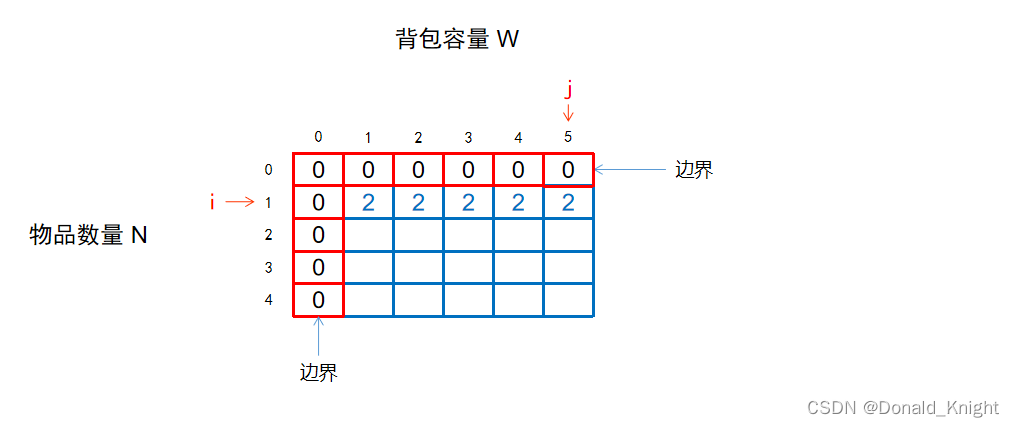
第1行全部完成后，我们让 i++，开始计算第2行。

首先计算f[2][1]

当 i=2，j=1时，表示：从前2个物品中选，总重量不超过1。
此时拆成两种情况：

（1）不选中第 1 个物品的情况：
等于【从前 1 个物品中选，背包容量为 1 时的最大价值】
此时，f[2][1] = f[1][1] = 2

（2）选中第 1 个物品的情况：
发现前提条件不满足：背包容量j >= 第i个物品的重量w[i]，即 if( j>=w[i] ) 为真不满足！

此时只有第一种情况，所以可知f[2][1]=2

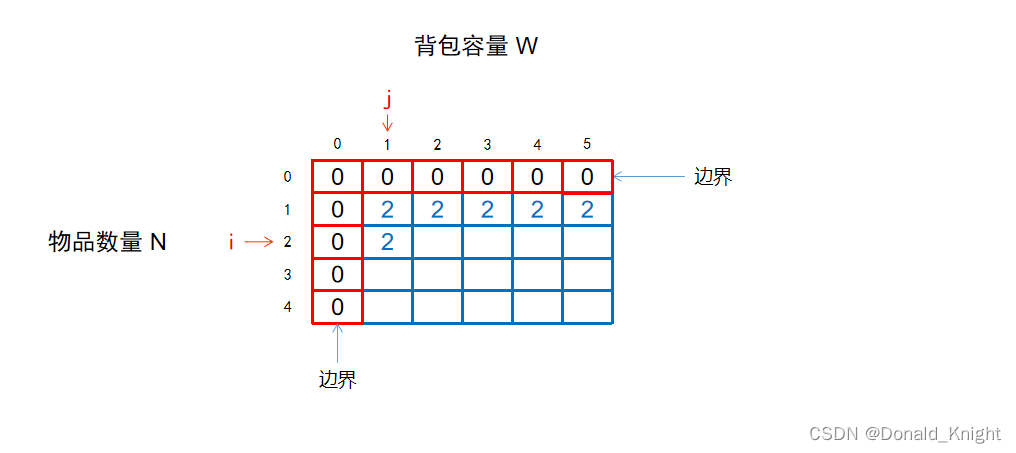
接下来我们让 j++，计算f[2][2]

当 i=2，j=2时，表示：从前2个物品中选，总重量不超过2。
此时拆成两种情况：

（1）不选中第 2 个物品的情况：
等于【从前 1 个物品中选，背包容量为 2 时的最大价值】
此时，f[2][2] = f[1][2] = 2

（2）选中第 2 个物品的情况：
前提条件：背包容量j >= 第i个物品的重量w[i]，即 if( j>=w[i] ) 为真，才可以选
等于【第i个物品的价值】+【从前 (i-1) 个物品中选，背包容量为 (j-第i个物品的重量) 时的最大价值】
此时，f[2][2] = v[2] + f[1][0] = 4+0 = 4

因此，最大价值解为 f[2][2] = max(2,4) = 4

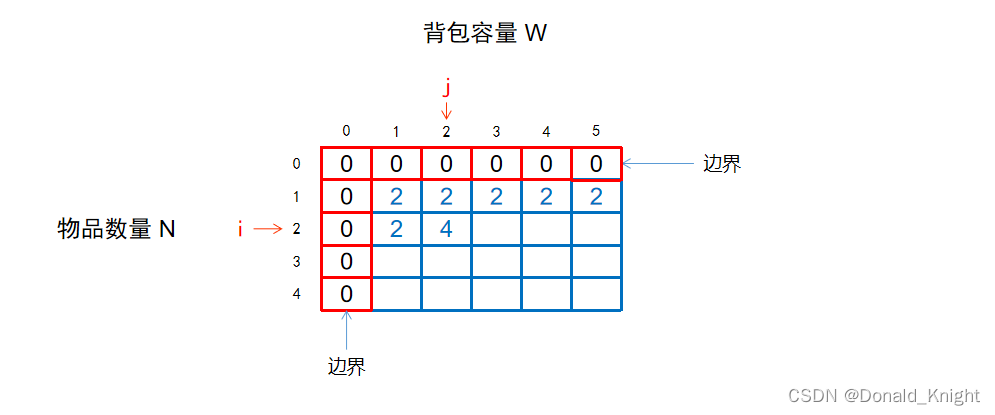
接下来我们再让 j++，计算f[2][3]

当 i=2，j=3时，表示：从前2个物品中选，总重量不超过3。
此时拆成两种情况：

（1）不选中第 2 个物品的情况：
等于【从前 1 个物品中选，背包容量为 3 时的最大价值】
此时，f[2][3] = f[1][3] = 2

（2）选中第 2 个物品的情况：
前提条件：背包容量j >= 第i个物品的重量w[i]，即 if( j>=w[i] ) 为真，才可以选
等于【第i个物品的价值】+【从前 (i-1) 个物品中选，背包容量为 (j-第i个物品的重量) 时的最大价值】
此时，f[i][j] = v[i] + f[i-1][j-w[i]]
此时，f[2][3] = v[2] + f[1][3-w[2]] = v[2] + f[1][3-2] = v[2] + f[1][1] = 4+2 =6

因此，最大价值解为 f[2][2] = max(2,6) = 6

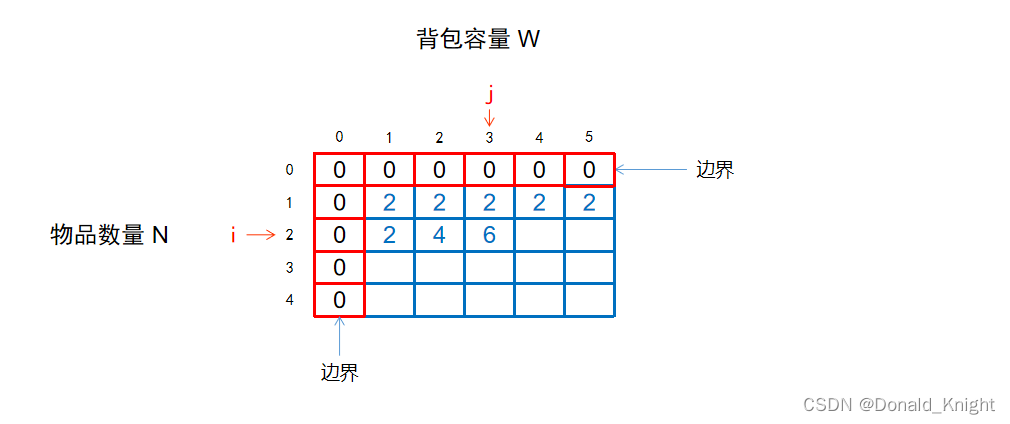
至此可以看出，在求解后边的答案时，会用到前边已经求出的结果！！！

继续求解，可求出第二行的所有结果。

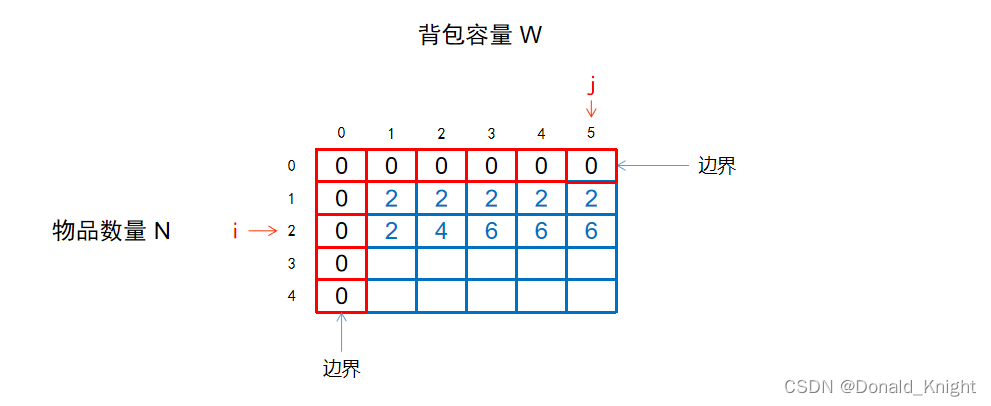
按照上边的道理，可以接着求出f[3][1]和f[3][2]

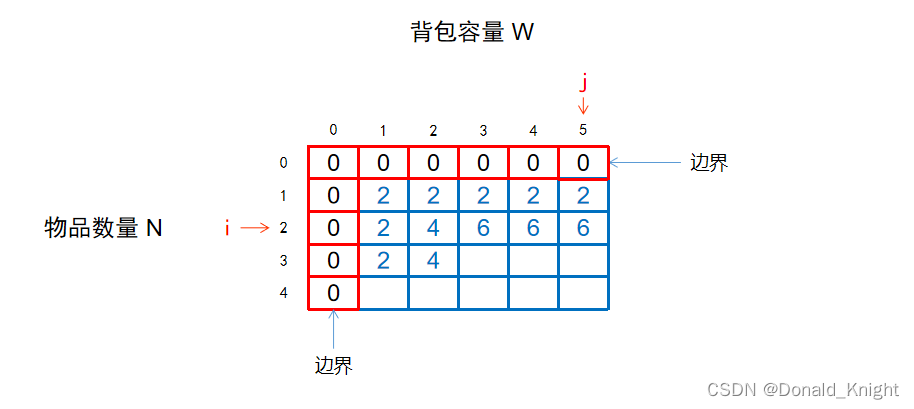
接下来我们重点看一下求解f[3][3]

当 i=3，j=3时，表示：从前3个物品中选，总重量不超过3。
此时拆成两种情况：

（1）不选中第 3 个物品的情况：
等于【从前 2 个物品中选，背包容量为 3 时的最大价值】
此时，f[3][3] = f[2][3] = 6

（2）选中第 3 个物品的情况：
前提条件：背包容量j >= 第i个物品的重量w[i]，即 if( j>=w[i] ) 为真，才可以选
等于【第i个物品的价值】+【从前 (i-1) 个物品中选，背包容量为 (j-第i个物品的重量) 时的最大价值】
此时，f[i][j] = v[i] + f[i-1][j-w[i]]
此时，f[3][3] = v[3] + f[3-1][3-w[3]] = v[3] + f[2][3-3] = v[3] + f[2][0] = 5+0 =5

因此，最大价值解为 f[2][2] = max(6,5) = 6

可以看出，在这种情况下，把3号物品放入背包的话，反倒会使最大价值减小！

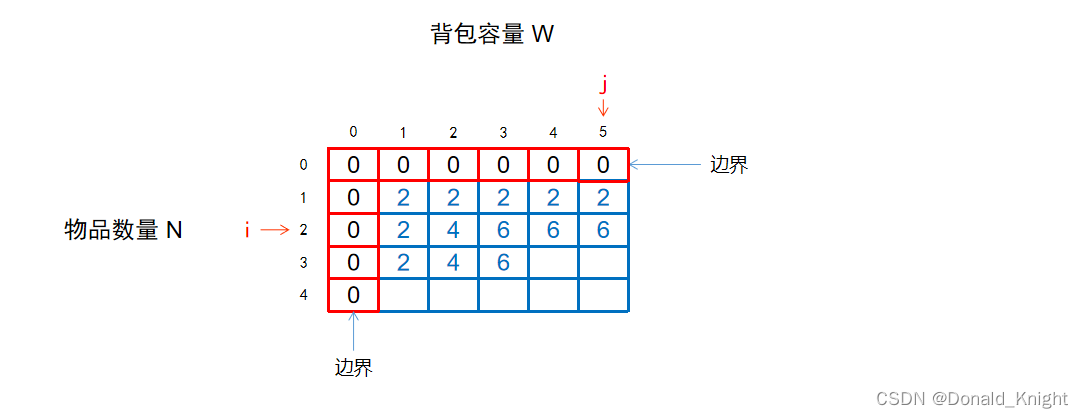
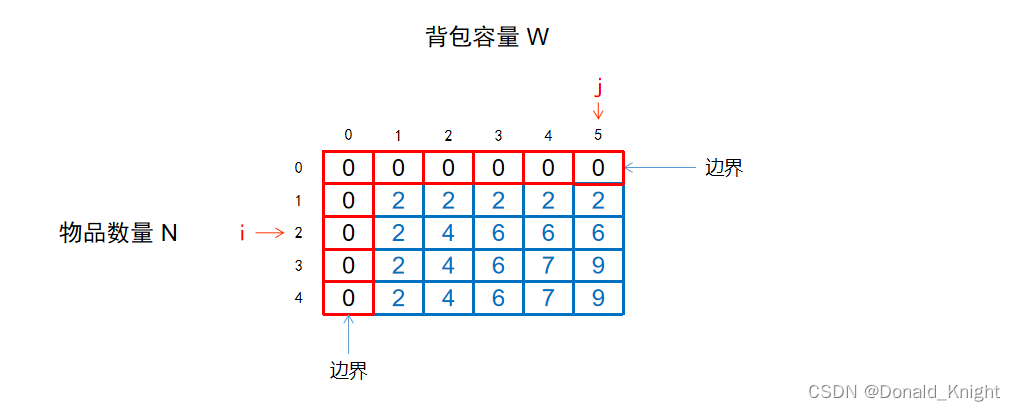
接下来的计算都是和上边相同的道理，依次求出二维数组中对应的所有结果。

#include <stdio.h>

#define N 4 //物品数量
#define W 5 //背包容量

int max(int a, int b) {
	if (a>b) {
		return a;
	} else {
		return b;
	}
}

int main() {

	//为了确保下标从1开始，第0号位上我们补一个0
	int v[] = {0, 2, 4, 5, 6}; //物品价值数组
	int w[] = {0, 1, 2, 3, 4}; //物品重量数组

	int f[N+1][W+1] = {}; //子问题解数组

	int i, j;

	for(i=1; i<=N; i++){
		for(j=1; j<=W; j++){
		
			//等于【不选择第i个物品】和【选择第i个物品】两者的较大者
			if(j>=w[i]){ //选择第i个物品的前提条件
				f[i][j]=max{f[i-1][j], f[i-1][j-w[i]]+v[i]};
			} else {
				f[i][j]=f[i-1][j]; //【不选择第i个物品】-->等于从前边的i-1个物品中选，背包容量为j时的最大价值
			}

		}
	}

	//输出f[4][5]的值
	printf("%d\n", f[N][W]); 	

	//输出整个二维数组查看效果
	for(i=0; i<=N; i++) {
		for(j=0; j<=W; j++) {
			print("%d ", f[i][j]);
		}
		printf("\n");
	}

	return 0;
}

还有另外一种写法

#include <stdio.h>

#define N 4 //物品数量
#define W 5 //背包容量

int max(int a, int b) {
	if (a>b) {
		return a;
	} else {
		return b;
	}
}

int main() {

	//为了确保下标从1开始，第0号位上我们补一个0
	int v[] = {0, 2, 4, 5, 6}; //物品价值数组
	int w[] = {0, 1, 2, 3, 4}; //物品重量数组

	int f[N+1][W+1] = {}; //子问题解数组

	int i, j;

	for(i=1; i<=N; i++){
		for(j=1; j<=W; j++){
		
			f[i][j]=f[i-1][j]; 		//默认【不选择第i个物品】
			
			if(j>=w[i]){ 	//选择第i个物品的前提条件
				//等于【不选择第i个物品】和【选择第i个物品】两者的较大者
				f[i][j]=max{f[i][j], f[i-1][j-w[i]]+v[i]}; 		//max()函数中的第一个值现在变成了f[i][j]
			} 

		}
	}

	//输出f[4][5]的值
	printf("%d\n", f[N][W]); 	

	//输出整个二维数组查看效果
	for(i=0; i<=N; i++) {
		for(j=0; j<=W; j++) {
			print("%d ", f[i][j]);
		}
		printf("\n");
	}

	return 0;
}

【0-1背包问题】的时间复杂度：O(NW)——即O(物品数量·背包容量)
【0-1背包问题】的空间复杂度：O(NW)——即O(物品数量·背包容量)

---

在【动态规划法】中，除了【0-1背包问题】，还会考到的是：
【最长公共子序列问题】
【矩阵连乘问题】

如果考到【矩阵连乘问题】的话：
【矩阵连乘问题】的时间复杂度：O(n^3)
【矩阵连乘问题】的空间复杂度：O(n^2)
计算方法：
最长公共序列：