寻找m序列的递推关系式。
已知一段序列,如果知道其反馈多项式,就可以将其后的序列依次求出
已知序列能否获得相应的反馈多项式(或线性递推式)呢?
- 解方程方法——已知序列{ai }是由n 级线性移存器产生的,并且知道{ai }的连续2n位,可用解线性方程组的方法得到反馈多项式
- 线性反馈移位寄存器综合解——Berlekamp-Massey算法
1 解方程方法
例1 设序列a = (01111000…)是由4级线性移存器所产生序 列的连续8个信号,求该移存器的线性递推式。

例 设敌手得到密文串: 101101011110010
和相应的明文串: 011001111111001
因此,可得相应的密钥流: 110100100001011
进一步假定敌手还知道密钥流是使用5级线性反馈移位寄存器产生的,那么敌 手可分别用密钥流中的前10个比特建立如下方程
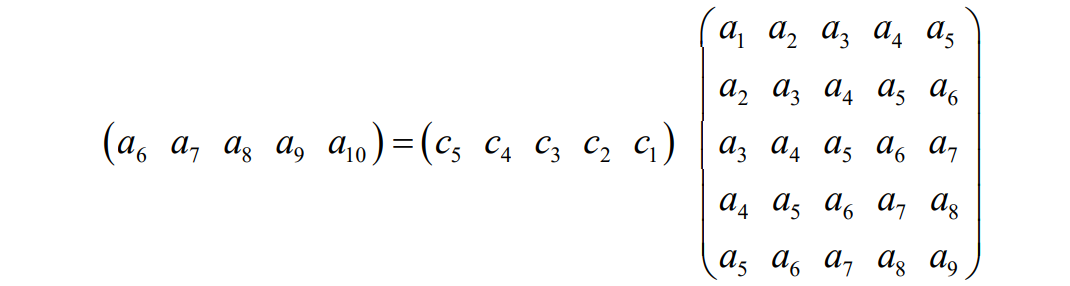
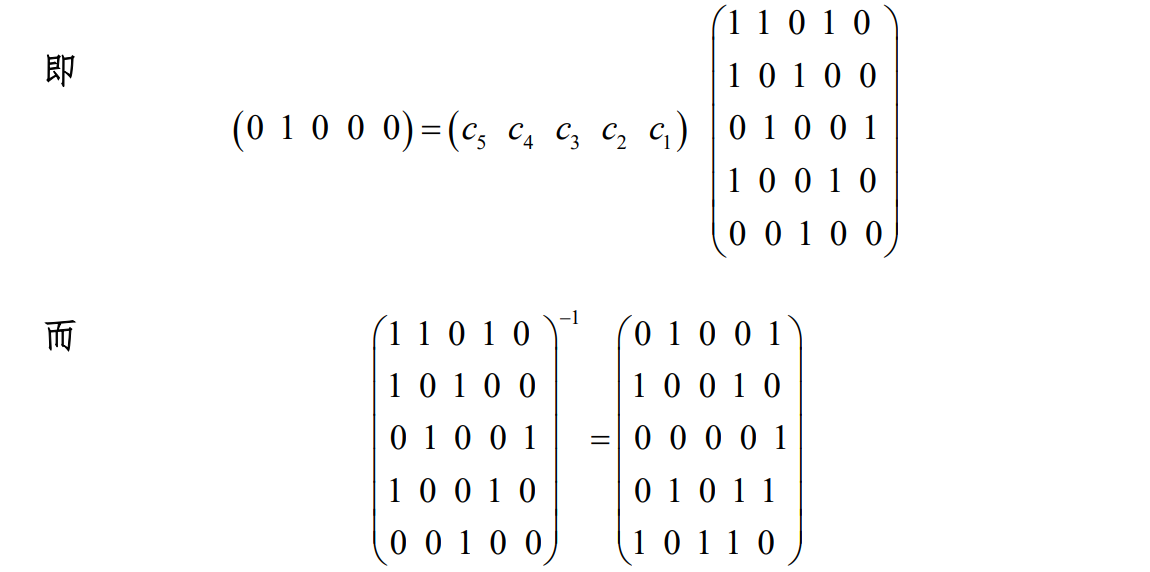

2 线性反馈移位寄存器综合
根据密码学的需要,对线性反馈移位寄存器(LFSR) 主要考虑下面两个问题:
(1)如何利用级数尽可能短的LFSR产生周期大、随机性能良好的序列。
这是从密钥生成角度考虑,用最小的代价产生尽可能好的、参与 密码变换的序列。
(2)当已知一个长为N序列a时,如何构造一个级数尽可能小的LFSR来产生它。
这是从密码分析角度来考虑,要想用线性方法重构密钥序列所必须付出的最小代价。
线性综合解

线性移位寄存器的综合问题

Berlekamp-Massey算法(B-M算法)



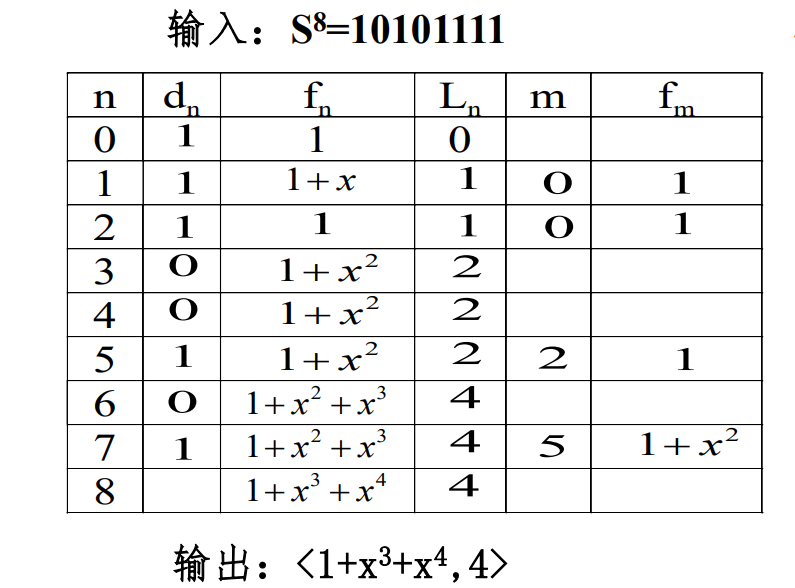
#include<stdio.h>
#include<string.h>
#define N 200
void printp(unsigned char *f,int n,int w)
{
int i,j=0,hflag=1;
for(i=0;i<=n;i++)
if(f[i])
{
if(!hflag)
{
printf("+");
j++;
}
else
hflag=0;
if(i>1)
{
printf("x^%-3d",i);
j+=5;
}
else
{
(i==1)?printf("x"):printf("1");
j++;
}
}
for(i=0;i<w-j;i++)printf("");
}
int main()
{
int L=0,LL,l,i,n,m;
char S[N];
unsigned char f[N+1],ff[N+1],g[N+1],d;
f[0]=1;
for(i=1;i<=N;i++)f[i]=0;
start:
printf("\n请输入长度不超过%d的比特串:\n",N);
scanf("%s",S);
l=strlen(S);
for(i=0;i<1;i++)
if(S[i]!='0'&&S[i]!='1')
{
printf("\n 输入数据不合法,须重来! \n");
goto start;
}
printf(" n dn fn ln m fm\n");
for(n=0;n<l;n++)
{
d=(S[n]=='0')?0:1;
for(i=1;i<=L;i++)
if(f[i]==1) d^=(S[n-i]=='0')?0:1;
printf("%3d %1d ",n,d);
printp(f,L,30);
printf("%3d",L);
if(d==1&&L!=0)
{
printf(" %3d ",m);
printp(ff,LL,30);
}
printf("\n");
if(d!=0)
{
if(L==0)
{
m=n;
for(i=0;i<=L;i++)ff[i]=f[i];
LL=L;
f[n+1]=1;
L=n+1;
}
else
{
for(i=0;i<=L;i++) g[i]=f[i];
for(i=0;i<=LL;i++) f[n-m+i]^=ff[i];
if(n+1-L>L)
{
m=n;
for(i=0;i<=L;i++)ff[i]=g[i];
LL=L;
L=n+1-L;
}
}
}
}
printf("%3d ",n,d);
printp(f,L,30);
printf("%3d\n",L);
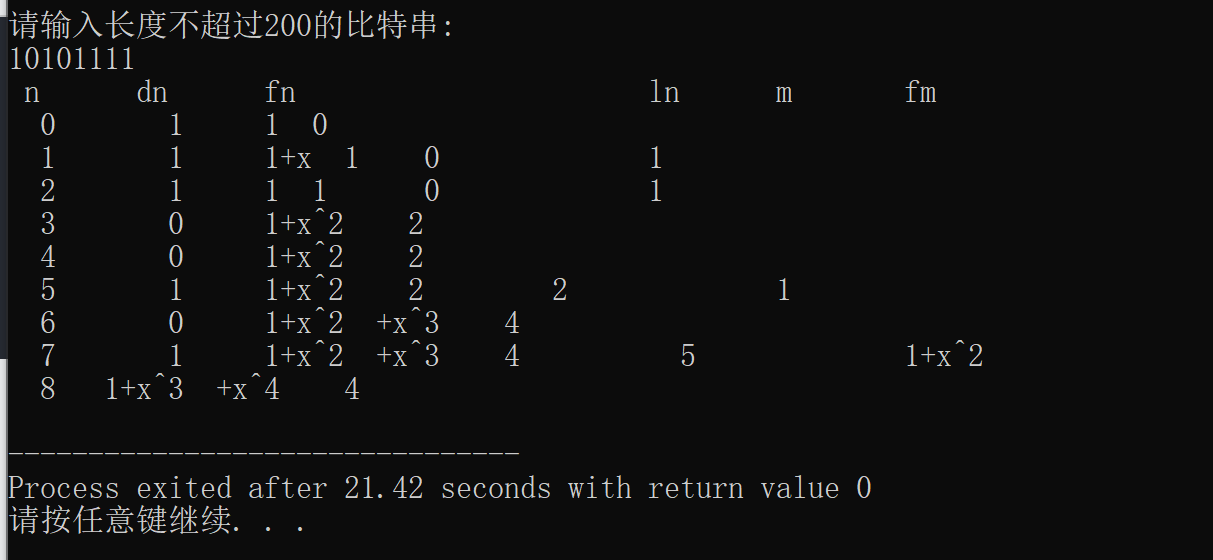
}





















 8727
8727











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








