按照《统计学习原理》一书中提到的机器学习三要素:模型、策略、算法。我认为最小二乘属于策略的范畴,这个策略就是求误差的最小平方和,对应两种情况:线性和非线性。线性情况下的解是closed-form solution(这种情况下可以找到全局最优解)。而非线性的情况没有closed-form solution,通常用迭代法求解(如梯度下降法)或将非线性最小二乘问题转化为线性最小二乘问题(一阶泰勒展开)。针对两种情况的不同求解方式其实就是算法。
下面来介绍一下线性情况下最小二乘法的矩阵形式公式推导:
首先给出一个线性模型的矩阵形式:
\[Y = AX\]
根据最小二乘得到:
\[L = {(AX - Y)^2}\]
\[\min L\]
因为极值点对应的导数为零,所以我们对L求偏导:
首先先将L变形
\[L = {(AX - Y)^T}(AX - Y)\]
然后展开
\[L = {X^T}{A^T}AX - {Y^T}AX - {X^T}{{\rm{A}}^T}Y + {Y^T}Y\]
接下来对上式求导,求导的过程中需要使用矩阵微积分的知识。
\[L' = 2{A^T}AX - 2{{\rm{A}}^T}Y = 0\]
所以解X必然满足:
\[{A^T}AX ={{\rm{A}}^T}Y \]
当m×n矩阵具有不同的秩时,上述方程的解有两种不同的情况。
情况1:矩阵A是超定的且是列满秩的rank(A)=n,那么可以得到唯一解:
\[X = {({A^T}A)^{ - 1}}{A^T}Y\]
矩阵A是超定的且是秩亏缺的rank(A)<n,最小二乘解为:
\[X = {({A^T}A)^{ - }}{A^T}Y\]
其中\[({A^T}A)^{ - }\]代表为矩阵的Moore-Penrose逆矩阵。
情况2:矩阵A是欠定的。这种情况不能得到唯一解。
Ps.矩阵微积分








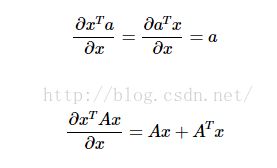














 3861
3861

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








