穆勒矩阵椭偏仪：DVRMME技术的系统误差建模与校准补偿

原创于 2025-11-10 10:10:05 发布 · 557 阅读

16 ·

CC 4.0 BY-SA版权

文章标签：

#偏振测量 #涡旋延迟器 #穆勒矩阵椭偏仪 #误差分析 #系统校准

椭偏仪专栏收录该内容

18 篇文章

订阅专栏

双涡旋延迟器穆勒矩阵椭偏仪（DVRMME）是一种先进的单次快照式全偏振测量技术。然而，其测量精度极易受到光学元件装配偏差和器件缺陷引入的系统误差影响。Flexfilm全光谱椭偏仪可以非接触对薄膜的厚度与折射率的高精度表征，广泛应用于薄膜材料、半导体和表面科学等领域。

本研究构建了一个包含六个关键系统误差参数（涉及起偏器、检偏器及两个涡旋延迟器的方位角与延迟量偏差）的全面误差模型。提出了两种穆勒矩阵重建方法：基于傅里叶系数分析的解析法，以及基于矩阵运算的数值法。通过一阶误差传播分析和雅可比矩阵，系统性地量化了各误差源对最终测量结果的影响，并证明利用双区平均测量策略可有效抵消部分误差。此外，本研究分别针对透射与反射两种典型测量模式，开发了具体的系统参数校准方案。仿真结果表明，即使在噪声干扰下，所提出的误差补偿框架也能显著提升穆勒矩阵的测量精度，为DVRMME的实用化奠定了坚实的理论基础。

实验理论与方法

穆勒矩阵能够最完备地描述材料对偏振光的作用，穆勒矩阵椭偏仪（MME）也因此成为前沿的光学测量工具。传统的双旋转补偿器MME（DRCMME）虽精度高，但受限于机械运动部件，测量速度慢。

本研究聚焦的DVRMME技术，利用两个不同阶数的涡旋延迟器进行空间调制，可在毫秒级时间内单次曝光获取全部16个穆勒矩阵元素，实现了测量速度的飞跃。

然而，前期研究大多基于光学元件参数理想的假设，忽略了实际应用中不可避免的加工与装调误差。为此，本文旨在系统性地解决DVRMME的三大核心问题：建立误差模型、分析误差传播规律、并提出有效的校准补偿方法。

DVRMME系统误差模型

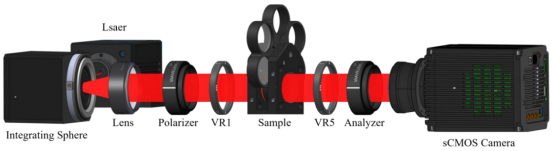
DVRMME的光路依次包含偏振态发生器（PSG，含起偏器与第一涡旋延迟器）、样品和偏振态分析器（PSA，含第二涡旋延迟器与检偏器）。我们建立的模型重点考虑了六个实际误差参数：

方位角误差：起偏器透射轴（θ1）、检偏器透射轴（θ4）的方位，以及两个涡旋延迟器快轴的初始方位（μ2,μ3）。

延迟量误差：两个涡旋延迟器偏离90°理想值的相位延迟（δ2,δ3）。

基于斯托克斯-穆勒形式体系，我们推导出包含这些误差的最终探测光强表达式：

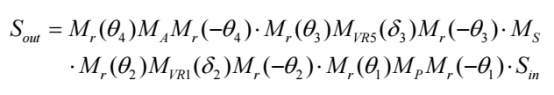
Sin是输入光束的斯托克斯矢量，Mp, MVR1, Ms, MVR2, MA分别代表光学元件的理想穆勒矩阵

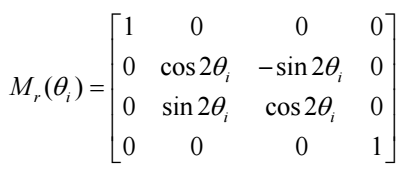
该表达式是样品穆勒矩阵元素 mij和所有系统误差参数的复杂函数，是后续分析与校准的基石。

两种穆勒矩阵重构方法

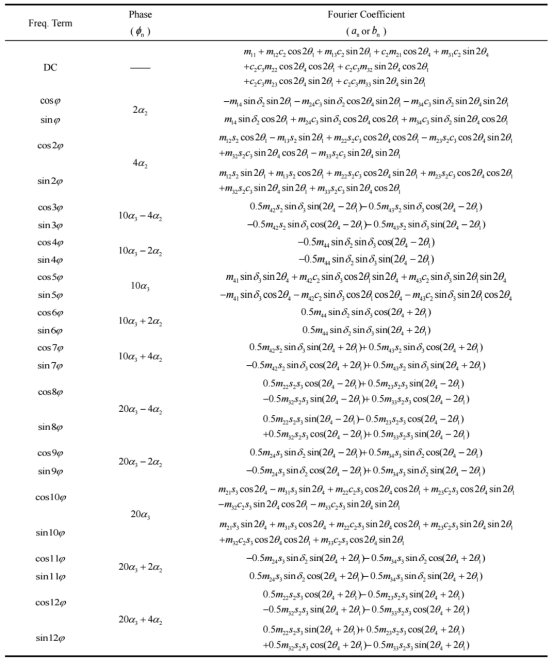
傅里叶分析法：探测光强随方位角 φ 的变化可展开为傅里叶级数。通过提取多达24个非零的傅里叶系数，并根据建立的查找表，可以解析地计算出所有归一化的穆勒矩阵元素。该方法物理意义清晰，是校准过程的基础。其表达式：

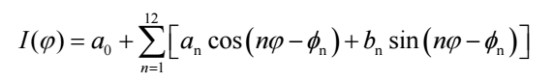
矩阵运算法：将整个系统建模为光强是PSA分析向量、样品穆勒矩阵和PSG产生向量的乘积。通过至少16次径向积分和一次矩阵求逆运算，可直接重构出穆勒矩阵。该方法计算效率通常更高，适用于快速数据处理。

根据误差模型，样品的穆勒矩阵Ms嵌入在一系列矩阵运算中，公式可重写为：

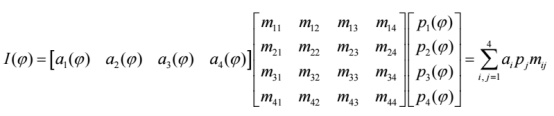
一阶系统误差分析

为了量化每个误差源的具体影响，我们采用一阶泰勒展开进行了灵敏度分析。关键结论包括：

方位角误差：除 m44外，几乎所有穆勒矩阵元素都会受到影响。分析表明，通过将起偏器（或检偏器）旋转90°进行两次测量并取平均（即双区平均法），可以完美消除由 θ1误差引起的 δm21,δm31,δm41误差，以及由 θ4误差引起的 δm12,δm13,δm14误差。

延迟量误差：若延迟器理想（精确为90°），则部分误差项自然消失。双区平均法同样可用于消除延迟量误差对某些特定矩阵元素（如第一列或第一行）的影响。

系统校准原理

透射模式校准：以空气（其穆勒矩阵为单位矩阵）作为标准样品。通过测量空气样品，提取其傅里叶系数，并利用它们与五个系统参数（μ2,μ3,θ4,δ2,δ3）之间的特定关系，可以精确反演出这些参数的实际值。

反射模式校准：通常使用已知穆勒矩阵结构的各向同性标准样品（如SiO₂薄膜）。通过分析测量得到的傅里叶振幅 ∣Rn∣和相位 Φn，可以求解出全部六个系统误差参数。

仿真验证与讨论

模拟强度图像所用的六个系统参数设定值

我们设置了接近实际的仿真条件（系统参数存在初始偏差，并加入不同强度的高斯噪声）来验证理论。

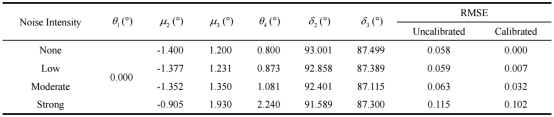
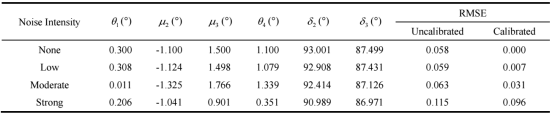
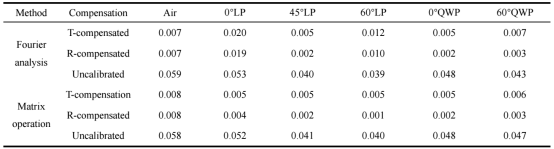
校准效果：在无噪声和低噪声情况下，无论是透射模式还是反射模式，所提校准方案都能非常准确地识别出系统参数，并将穆勒矩阵的均方根误差（RMSE）降至极低水平。

抗噪性能：随着噪声增强，参数识别精度和校准效果会有所下降，但在强噪声下，校准后的RMSE仍显著低于未校准状态，证明了方法的鲁棒性。

方法对比：对比两种重构方法发现，使用反射模式校准参数（R-compensated）普遍能获得更优的补偿效果。对于复杂样品，矩阵运算法在精度上略优于傅里叶分析法。因此，一个优化的策略是：利用傅里叶分析进行系统校准，然后采用矩阵运算法进行快速的穆勒矩阵计算。

本研究为DVRMME建立了一套完整的误差分析与补偿理论框架。通过建立六参数误差模型、提出两种矩阵重构方法、进行详尽的一阶误差分析并开发针对透射/反射模式的校准方案，系统性地解决了该技术走向实用化的关键理论障碍。仿真结果验证了所提方法在提升测量精度和抗干扰能力方面的有效性与可行性，为后续的实验研究和高精度应用提供了重要指导。