数二-线代

一、行列式

一.性质

二.易混

1.代数余子式和余子式

余子式，即去掉i行j列后余下的行列式拼成的子式。

代数余子式，即在余子式前面加上符号。

行列式，等于某一行（列）代数余子式之和。

三.一些重要行列式

1.主对角线。副对角线=

2.拉普拉斯（分块）

3.范德蒙行列式（成比列变化）

二、矩阵

初等矩阵的逆矩阵

1）对于倍加类型的初等矩阵，其逆矩阵是原初等矩阵对应行变相反数的矩阵，即多出来的加个负号；

2）互换类型的初等矩阵，其逆矩阵是自身；

3）对于倍乘类型的初等矩阵，逆矩阵是原矩阵对应行乘以倒数。

正交矩阵

，即

三、矩阵的秩

关于秩的结论：

1），则

2）

3）矩阵A秩为1

4）r() =r(A)

四、线性方程组

一.解的结构

1）基础解系

2）通解：基础解系的线性组合

非齐：特解+齐次通

二.通解的技巧

1）根据自由未知量个数写出通解样式：非齐特+齐通

2）将自由未知量填为1，0；其它值由1所在列反号顺抄

3）非齐特：自由未知量为0，其它顺抄常数项

知识点：

1.任意A*B=0，则B就是矩阵A的解；

2.齐次线性无关解数量 = n-r ，非齐次线性无关解数量 =  n-r+1；

五、向量组和线性方程组的一些结论

一.极大线性无关组

二.等价问题

1.同解

2.矩阵等价

矩阵等价、相似、合同的定义及性质_两个矩阵相似有哪些性质-CSDN博客

矩阵A经过有限次初等变换得到矩阵B，即，PAM=B，则A与B等价。（初等变换可逆）

r(A)=r(B)

3.向量组等价

两个向量组可以相互线性表示。

向量组中向量的个数不要求相等，但极大线性无关组相等。

4.矩阵相似

5.矩阵合同

相似：特征值完全相同

合同：特征值仅符号相同

正交变换：既合同又相似

六、特征值和特征向量、相似矩阵

一.特征值的求解

1.|ʎE-A|=0，求出ʎ。

2.带入ʎ，求出(ʎE-A)α=0对应的特征向量。特征向量即齐次方程的基础解系。

二.特征值的重要性质 

1.矩阵A的主对角线之和(迹)等于特征值之和。tr(A)=特征值之和。

2.矩阵A的行列式等于特征值之积。|A|=特征值之积。

三.相似矩阵 

1.定义

2.性质

3.重要结论

4.相似判定

四.矩阵的相似对角化

1.性质

2.可相似对角化的条件

1）充要条件：矩阵A有n个线性无关的特征向量；

2）充要条件：矩阵A每个k重的特征值，对应有线性无关的k重特征向量；

3）充分条件：矩阵A有n个不同的特征值；

4）充分条件：矩阵A为实对称矩阵。

3.求可逆矩阵P，使矩阵A相似对角化，即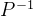AP=⋀

求P，即求矩阵A的特征值及特征向量

1）求矩阵A的特征值，求出其特征向量

2）由特征向量组合成为P

4.由特征值、特征向量反求矩阵A

1）有特征值即有⋀，有特征向量即有P。而AP=⋀

2）矩阵A=P⋀

五.实对称矩阵的相似对角化

1.性质

1）实对称矩阵A的属于不同特征值的特征向量相互正交

2）任意的实对阵矩阵A均可相似对角化

2.实对称矩阵相似对角化步骤

1）求特征值、特征向量

2）将特征向量正交化（可用施密特正交化法或直接观察，见1000基础6t）、单位化

3）将特征向量拼成Q

3.谱分解

七、二次型

一.合同变换、标准型、规范型（概念见1000线代基础二次型讲解视频）

1.合同

1）定义

2）性质

1.合同，则秩相同

2.合同矩阵，必是实对称矩阵（考研中）

3.r(A)=r(B)

4.合同，则正负惯性指数相同，则规范型相同

3）合同判别

两个二次型（即实对称矩阵）合同的充要条件

1.具有相同的正、负惯性指数

2.或有相同的秩及正（或负）惯性指数

3.或有相同的正、负特征值个数

2.标准型、规范型

1）定义

标准型：除了对角线元素，其余全为0；

规范型：除了对角线元素，其余全为0，且对角线取值{-1，0，+1}。

2）定理（配方法和正交变换）

 1.任意二次型均可通过配方法化成标准型及规范型

2.任意二次型均可通过正交变换化成标准型及规范型

 

 3.标准型和规范型的求解

1）配方法

1.一定可化成规范型

配方法求解可逆矩阵P的求解框架：

2）正交变换法及一些相关问题的求解

正交变换法求解标准型的步骤：

1.将矩阵化为二次型，求矩阵的特征值。所得特征值即为正交变换后标准型的系数。若系数全为{±1，0}，则为规范型。

2.求特征值对应的特征向量，并将特征向量正交化、单位化，所得向量拼成线性变换Q矩阵。

 ps：

1.正交变换后标准型的系数必是矩阵A的特征值。且正交变换不一定可化成规范型。

正交变换法求解正交矩阵Q求解框架：

3）特征值法求规范型 

1.可逆的线性变换不改变正负惯性指数。求得特征值，即得到正负惯性指数的个数，即得到规范型的形式。 

4）配方法和正交法的对比

二.惯性定理

1）求惯性指数的相关问题

1.使用配方法，看其平方项的正系数个数

2.求二次型矩阵A的特征值，看正特征值的个数

三.正定二次型及其判别

正定，即函数f恒大于等于0

1.性质

2.必要条件

1）主对角线元素＞0；

2）|A|＞0 

四.二次型最值问题