Generic Programming简介
——Douglas Gregor
原文:http://www.generic-programming.org
Generic Programming (GP;泛型编程)是一种开发高效可复用软件库的编程泛式,由Alexander Stepanov 和 David Musser 所创造。在标准模板库(STL)成为 ANSI/ISO C++ 标准一部分的时候, GP 技术取得了首次成功。从那以后,泛型编程泛式就被用来开发各种通用程序库了。
泛型编程的过程集中在找出同一算法的相似实现中那些共同的代码,然后以 concept的形式提供一种合适的抽象形式,这样,一个单一的泛型算法就能应用于多种具体的实现。不断重复这个被称为 lifting (提升?)的过程,直到这个泛型算法达到一个合适的抽象级别,这时它能在不牺牲性能的情况下提供最大的可复用性。二次提升是一个 Specialization (特化)的过程,为一个泛型算法的某一特定应用生成高效而且特别的实现。只有实现 lifting 和 Specialization 过程的平衡,我们才能确保最终的泛型算法既可复用又高效。
内容列表
Lifting
Concepts
Models
Specialization
结论
Lifting
Lifting 基本类型
Lifting 容器
Lifting iterator(迭代器)
回顾总结
Lifting 过程是 GP 过程的第一步也是最重要的一步。Lifting 通过下面的这个基本问题试图发现一个通用的算法。
要使算法能正确操作且高效地运行,我的数据类型至少要实现些什么?
Lifting 基本类型
对于一些常见的一般的算法,偶尔可能猜到它的最低要求并且直接实现一个泛型算法。但是,对于任何现实的算法,lifting 是一个从同一算法的许多的、具体的实现开始的一个迭代过程。例如,考虑下面两个求和算法的 C++ 实现。在这个教程中我们将使用 C++ 作例子,因为它是最容易获得的很好地支持了GP的语言。
int sum(int* array, int n) {
int result = 0;
for (int i = 0; i < n; ++i)
result = result + array[i];
return result;
}
float sum(float* array, int n) {
float result = 0;
for (int i = 0; i < n; ++i)
result = result + array[i];
return result;
}
这两个函数几乎是一模一样的,除了上面的 sum() 实现应用于整数而下面的 sum() 则应用于浮点数。我们现在可以 lifting 这两个算法来创造一个单一的泛型算法,来提供这两个版本的 sum() 的功能。为此,我们用一个类型参数 T 来替换 int 和 float ,使用 C++ 模板来做是这个样子的:
template<typename T>
T sum(T* array, int n) {
T result = 0;
for (int i = 0; i < n; ++i)
result = result + array[i];
return result;
}
templete<typename T> 可以理解为"所有的类型 T",但这样说并不严格。当我们从具体的sum() 的实现 lifting 到这个泛型实现时, 我们需要指出要使用sum() ,类型T应该支持哪些操作。要找到这些要求,我们查找函数体内使用类型T的操作。下面的代码,我们把这些操作高亮成红色:
template<typename T>
T sum(T* array, int n) {
T result = 0;
for (int i = 0; i < n; ++i)
result = result + array[i];
return result;
}
因此,给定一个类型T,要使用sum() ,我们需要它能够用0初始化(第一个红色的行),两个类型T的值相加(使用operator+),然后将结果赋值给一个T(用operator=);最后,我们需要能够从函数返回一个类型为T的值,这要求有一个拷贝构造函数。我们的泛型sum()能够与许多种类型一同工作,包括(显然)int和float,以及long,double,或者其它任何满足我们上面说过的那些要求的类型。
要更深入地lifting这个算法,我们需要将它与其它的求和算法的具体实现相比较。比如,让我们考虑这样一个函数,它能将一批字符串连接到一起。
template<typename T>
T sum(T* array, int n) {
T result = 0;
for (int i = 0; i < n; ++i)
result = result + array[i];
return result;
}
std::string concatenate(std::string* array, int n) {
std::string result = "";
for (int i = 0; i < n; ++i)
result = result + array[i];
return result;
}
这两个算法又一次几乎一样,除了我们的泛型算法需要数字类型,即它能够用零初始化,而连接函数算法操作字符串,且用空字符串初始化。我们怎样lift我们的泛型算法才能使它能够处理字符串?我们需要抽象掉初值,于是数字类型将用零初始化,而字符串则用空字符串初始化。在所有这些情况中,默认构造函数提供了正确的值,所以我们要修改我们的泛型算法来满足新的要求:
// 要求:
// T 必需有一个默认构造函数,且产生相同的值
// T 必需有一个加法操作符
// T 必需有一个赋值操作符
// T 必需有一个拷贝构造函数
template<typename T>
T sum(T* array, int n) {
T result = T();
for (int i = 0; i < n; ++i)
result = result + array[i];
return result;
}
lifting 容器
我们的泛型算法现在支持数字量的求和,连接字符串等操作,它还能支持数组和矩阵及其它数据类型的加法运算。但它仍只支持C++的数组。那么其它数据结构呢,比如vector或list?因为vector支持和数组一样的索引方式,所以我们就能lift我们的泛型算法来支持数组,vector和任何其它支持索引操作符 operator[] 的“容器”类型。
// 要求:
// T 必需有一个默认构造函数,且产生相同的值
// T 必需有一个加法操作符
// T 必需有一个赋值操作符
// T 必需有一个拷贝构造函数
// 容器必需有一个返回一个T值的索引operator[]
template<typename Container, typename T>
T sum(const Container& array, int n) {
T result = T();
for (int i = 0; i < n; ++i)
result = result + array[i];
return result;
}
我们的新泛型算法能与std::list一起工作吗?非常不幸的是,不能。因为std::list没有提供一个索引操作符。假设我们能够改变std::list使它提供一个索引操作符,虽然这样做严重违反了GP的原则:一个泛型算法不应该要求类型拥有一个不改变类型的定义就不能“添加”的功能。尽管如此,如果我们修改了std::list来提供一个索引operator[] ,这个泛型sum算法将产生正确的操作。
Lifting 迭代器
在我们的sum算法里使用std::list时还有另外一个问题。考虑如何为一个连接列表实现索引操作符:来找到第i个元素,一个可行的算法是遍历列表中的i个项。这是一个线性时间的操作。如果我们使用这个list调用sum函数,求和将要花费二次方的时间!算法是正确的,但并不高效,这意味着我们的算法不是过度抽象(因此实现了一个更通用但不高效的算法)就是抽象不足。让我们回到开始,对比一下基于数组的sum实现和链表的sum实现:
template<typename T>
T sum(T* array, int n) {
T result = T();
for (int i = 0; i < n; ++i)
result = result + array[i];
return result;
}
template<typename T>
struct list_node {
list_node<T>* next;
T value;
};
struct linked_list {
list_node<T>* start;
};
template<typename T>
T sum(list_node<T> list, int n) {
T result = 0;
for (list_node<T>* current = list.start;
current != NULL; current = current->next)
result = result + current->value;
return result;
}
与以前那些实现相比,这两个实现有许多的不同之处。比如,迭代器方式是完全不同的,在一个简单的循环里,数组使用整数循环,而链表则用一系列指针的跳转。并且容器本身的角色在链表版的循环里也小得多:一但得到链表的开始,链表对象本身就不再被引用。第二个不同是找到一个更好的抽象的关键问题:我们已经尝试过(并且失败了)使容器成为核心的抽象,但是如果迭代器成为一个序列容器的核心抽象呢?我们能再把基于数组的sum转换成更关注于迭代器而不是容器的算法吗?来看看下面的代码:
templete<typename T>
T sum(T* array,int n){
T result = T();
for (T* current = array; current != array + n; ++current)
result = result + *current;
return result;
}
两个具体算法现在大体上已经有了相同的形式:有一个我们用来迭代容器内所有元素值的东西,它有一个访问当前元素的方法(即用*解引用或检索value成员),有一个跳到下一个元素的操作(即用++增加一个指针,或跳到链表的next指针),和一个测试到达序列末尾的操作(NULL或array+n)。如果我们抽出这些操作并给它们起了名字,我们就能写出一个通用的sum算法,它既能很好地和基于数组的序列一起工作,又能和链表和平相处:
// 要求:
// T 必需有一个默认构造函数,且产生相同的值
// T 必需有一个加法操作符
// T 必需有一个赋值操作符
// T 必需有一个拷贝构造函数
// T 必需有一个不等于操作符
// T 必需有一个能移动到序列的下一个值的操作next()
// T 必需有一个能返回当前值(类型为T)的操作get()
templete<typename I, typename T>
T sum(I start, I end, T init){
for (I current = start; current != end; current = next(current))
init = init + get(current);
return init;
}
现在,我们只需要为指针和链表节点指针写get()和next()函数就可以了。然后我们的sum算法将会高效地操作链表、数组和其它任何数据结构,只要它们的元素能通过它们线性地访问,且get()、next()和!=能高效地实现就可以了。
templete<typename T> T* next(T* p) { return ++p; }
templete<typename T> list_node<T>* next(list_node<&>* n ) { return n->next; }
templete<typename T> T get(T* p) { return *p; }
templete<typename T> T get (list_node<&>* n) { return ->value; }
在这个最后的lifting的步骤里,我们介绍了一个新的模板类型参数 I。在C++ 标准模板库中的术语中,I叫作迭代器。迭代器是一个遍历一个序列中的值的抽象,能够用来访问存储在多种容器中的元素,从动态数组和链表到平衡二叉树和hash表。将存储值(容器)从访问这些值(迭代器)里分离出来。它能够写出操作任何容器的代码。
回顾总结
我们最原始的sum()实现只支持存储在数组里的简单的数字数据类型。通过lifting的过程,我们能够使用一个operator+来拓展它的实用性到其它的操作,比如字符串连接。通过引进迭代器——非容器访问——到要求中,我们还能lifting掉它对数组的依赖。我们最终的suming算法能够操作许多不同类的容器,存储着多种不同的数据,并保持一个专门的具体的实现的高效。
GP的lifting过程集合同一算法的许多具体的实现,整理出算法对它们的参数的最低要求。继续阅读下面的课程来学习这些从lifting中找出的要求如何组合和归类到concept,提供一个问题域中关于核心抽象的描述。
Concepts
Concepts
嵌套要求
相关类型
refinement(精炼)
concept将前后一致的要求的集合收集到一起,放入一个单独的实体中。concept基于抽象的行为描述了一族相关的抽象。比如,一个iterator的concept应该描述迭代遍历序列中的值的抽象(比如一个指针),一个socket的concept应该描述通过网络传输数据的抽象(比如一个IPv6 socket),一个多边形concept应该描述闭平面图的抽象(比如三角形和八边形)。
concept既不能发明也不能创造。它们是通过lift同一领域中许多算法的过程中发现的。lift过程的结果是得到一个泛型算法,和一组要求。下面这个算法是在上一节中lift sum算法得到的:
// 要求:
// T 必需有一个加法operator +
// T 必需有一个赋值操作符
// T 必需有一个拷贝构造函数
// I 必需有一个不等于操作符operator !=
// I 必需有一个拷贝构造函数
// I 必需有一个赋值函数
// I 必需有一个能移动到序列的下一个值的操作next()
// I 必需有一个返回当前值的操作(类型为T)get()
template<typename I, typename T>
T sum(I start, I end, T init) {
for (I current = start; current != end; current = next(current))
init = init + get(current);
return init;
}
有很多方法可以将这些要求打包放入一个或多个concept中。一方面,我们能创建一个sum concept,它包括了完整的要求列表。另一方面,每个要求可以保存在它自己的concept中。通常,正确的做法是这两种的一个折中:一个concept应该包括足够的要求从而使它所描述的抽象能够得到广泛地认同。太也不能包括太多的要求以致抽象族受到不必要的限制。
当我们想把要求打包进concept,我们仍然要依赖于lift过程。但是,这次我们关注于不同算法中的要求。比如,下面的例子演示了在一个序列中查找一个值的算法的lift结果:
// 要求:
// T 必需有一个相等操作符
// T 必需有一个拷贝构造函数
// I 必需有一个不等于操作符
// I 必需有一个拷贝构造函数
// I 必需有一个赋值操作符
// I 必需有一个能移动到序列的下一个元素的next()操作
// I 必需有一个返回当前值的(类型为T)的get()操作
template<typename I, typename T>
I find(I start, I end, T value) {
for (I current = start; current != end; current = next(current))
if (get(current) == value)
return current;
return end;
}
比较find() 和set()的要求集,我们会发现很多相似及一些显著的不同。比如,要求类型T具有一个operator+只出现在sum()中,而要求有一个operator==则只出现在find()中。但是,无论是sum()还是find(),都要求类型T具有一个拷贝构造函数,因此就能用相同的concept来描述这个要求。再来看I的要求,我们可以发现,两个算法中的I的要求是相同的。因此,I 的所有要求都能装入一个concept中,我们可以叫它 Iterator concept。下面的表格将这些要求分类放入一些初步的concept中。我们可以使用标识符ConceptName<T1,T2,...,TN>来表示我们将用与ConceptName相关联的要求来约束类型T1,T2,...,TN。如果只有一个类型T,我们简单地描述为“T是一个ConceptName”。
| Concept | Requirements |
| CopyConstructible<T> | T must have a copy constructor |
| Assignable<T> | T must have an assignment operator |
| Addable<T> | T must have an operator+ that takes two T values and returns a T |
| EqualityComparable<T> | T must have an operator== comparing two Ts and returning a bool. |
| Iterator<I, T> | I must have an operator== comparing two Is and returning a bool. |
使用上面描述的concept,我们可以彻底简化sum()和find()的要求的的描述,像下面这个样子:
// 要求: Addable<T>, Assignable<T>, CopyConstructible<T>, Iterator<I, T>
template<typename I, typename T>
T sum(I start, I end, T init);
// 要求: EqualityComparable<T>, Assignable<T>, CopyConstructible<T>,
// Iterator<I, T>
template<typename I, typename T>
I find(I start, I end, T value);
通过把相关的要求打包进concept,我们就可以简化关于算法的要求的表达,并给出一些抽象的一致的描述。类型 I 是一个迭代器,类型T是一个可加的,等等。concept也表达了算法之间的关系:sum()和find()都操作于一个单一的值的序列来计算出结果。
嵌套要求
我们初步的concept的表格中有一些不必要的冗余。比如,迭代器concept有operator== 和operator !=,以及一个拷贝构造函数,这些已经在其它的concept中定义过了。我们可以通过嵌套要求的方法,在定义其它concept时复用前面的concept。一个嵌套要求是在当一个concept引用其它concept作为它自己的要求时的方法,比如,Iterator<I,T> concept要求EqualityComparable<I>。使用嵌套要求, 我们可以更改 Iterator concept为下面的定义:
| Concept | Requirements |
| Iterator<I, T> | EqualityComparable<I>, CopyConstructible<I>, Assignable<I> |
相关类型
在lift更多算法时使用concept做为辅助是一种发现concept要求中的弱点的非常好的方法。 在Iterator concept这个例子中,它其它是一个完全没有意义的算法,可以找到第一个问题:distance()函数,用来算法一个序列的长度。
// 要求: Iterator<I, T>
template<typename I, typename T>
int distance(I start, I end) {
int i = 0;
for (; start != end; ++start)
++i;
return i;
}
distance()函数的问题是:它几乎不能使用。因为在函数的声明中没有T的引用,用户被强迫提供一个类型T(即,get()的返回类型),即使它从来都没有用过。提供一个额外的类型只不过是一个小麻烦,但是当concept变得起来越复杂时,伴随着许多的额外的类型,这个麻烦将变成一个严重的问题。
相关类型解决了concept有太多的参数的问题,通过允许特定的类型存储在concept的定义里。这些类型在需要它们时,总是可以获得的,但它们不是用来特化concept的。比如,一个迭代器的get()函数的返回类型(前面我们称之为T)能够做成一个相关类型,我们称之为value_type。泛型算法能够使用一个迭代器的value_type,但当他们不需要它时,他们就不需要指定它了。下面是一个改进的Iterator concept。对象要注意的是,我们已经忽略了来自Iterator<I,T>中的类型T
| Concept | Requirements |
| Iterator<I> | EqualityComparable<I>, CopyConstructible<I>, Assignable<I> |
使用新定义的Iterator,我们能够更加简单地表达distance()算法:
// 要求: Iterator<I>
template<typename I>
int distance(I start, I end) {
int i = 0;
for (; start != end; ++start)
++i;
return i;
}
在C++中,相关类型被存储在类模板中,称作traits(特征)。Traits是辅助类模板,它能够被特化来检索相关类型,查找一个特殊的concept使用。例如,一个迭代器的value_type能够通过iterator_traits数据结构来访问。例如,下面这个sum()的实现,使用了iterator_traits来访问value_type。
// 要求: Iterator<I>, Addable<value_type>, Assignable<value_type>,
CopyConstructible<value_type>
template<typename I>
typename iterator_traits<T>::value_type
sum(I start, I end, typename iterator_traits<T>::value_type init) {
for (I current = start; current != end; current = next(current))
init = init + get(current);
return init;
}
相关traits到一个类型可以通过C++的特化机制来实现。比如,下面一个类模板的偏特化描述了一个指针T*(是一个迭代器)的value_type是T:
template<typename T>
struct iterator_traits<T*> {
typedef T value_type;
};
refinement(精炼)
嵌套要求允许我们复用concept来描述其它的concept。嵌入要求能够表达任意的concept要求,但是我们常常需要一个更加确定的等级关系。concept refinement描述了两个concept之间的等级关系。如果一个concept C2 细化了一个concept C1,那么C2就包括了C1的所有的要求,并且添加了它自己的要求。所以,每个C2也是一个C1,但C2更加具体,并且大概能够产生更多更好的算法。
考虑一下我们在前面已经设计出来的迭代器concept。它允许向后移动,并读取每个值。但是,如果我们想要改变一个值或向前移动,那要怎么样做?如果我们添加这两个操作,set 和prev,到Iterator,我们能够实现一个reverse()算法,它可以反转一个序列中的元素。但是,我们将创建一个新的concept BidirectionalIterator,而不是让Iterator变得巨大,它细化了Iterator,添加了下面两项:
| Concept | Requirements |
| BidirectionalIterator<I> | Refines Iterator<I> |
使用这个新的concept,我们能够表达reverse算法:
// 要求: BidirectionalIterator<BI>, Assignable<value_type>, CopyConstructible<value_type>
template<typename BI>
void reverse(BI start, BI end) {
while (start != end) {
end = prev(end);
if (start == end)
break;
// 交换值
typename iterator_traits<BI>::value_type tmp = get(start);
set(start, get(end));
set(end, tmpl);
start = next(start);
}
}
每个BidirectionalIterator 都是一个Iterator,但反回来却不成立:比如一个单向链表的Iterator,能够修改值(要求有set())但不能向前移动(prev())。类似的,一个常量值的双向链表的Iterator可以向前移动,但不能改变它的值。
小心地lift许多泛型算法将会得到正确的要求的分包,放入concept中。并且concept之间的等级关系将通过细化来表达。细心地分析标准模板库将得到下面的迭代器concept关系图。这里,C2->C1表示C2细化自C1。当我们有许多已经准备好的放在一个或几个体系中的concept时,我们可以称之为concept分类系统。
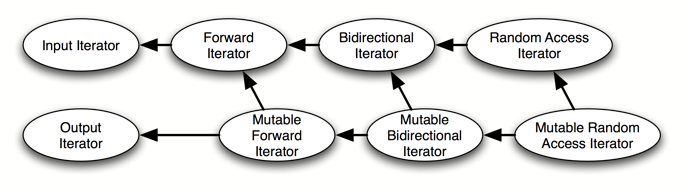
Models
concept描述了一族抽象所满足的一组要求。这些抽象代表了基本数据类型或数据类型集,我们称之为models。例如,一个指针就是Iterator concept的一个model;我们也可以说一个指针model了Iterator concept。
GP中一个重要的方面就是一个给定的concept的model集既不是已知了也不是固定的。一个concept是由一个小的已知的model集写成的——比如说,一个链表中的节点和指向数组的指针——但是它却要应用到许多许多其它的数据类型,比如一个二叉树的前序迭代。一个共识是GP适合于设计开发复用库,因为一个泛型算法能够同任何concept要求的model同等地友好工作,不管算法的作者是否考虑过那些数据类型。当我们在前面开发sum()算法的时候,应用了这个指导思想,我们是否意识到它能够应用到从文件中读取的整数,或者通过网络,甚至是通过重复调用随机数生成器产生的呢?任何数据类型,只要实现了那些操作,就能成为Iterator concept的model,因而就能同我们的sum()算法一同工作。
同样的,当一个数据类型被创建时,我们不需要知道它要满足的所有的concept。如果我们发现需要让这个类型满足一个新的concept,我们可以实现需要的语法而不是改变我们的数据类型。这种能力称为retroactive modeling,它允许任何人去适应已经存在的数据类型,为了使用泛型算法。比如,回去看一下我们是怎样为指针添加迭代器操作和相关类型的:我们没有修改指针的定义,我们也不能那样做,因为它是一个内建的类型。通过使我们所有的要求扩展到这个数据类型,我们允许retroactive modeling并避免强行修改已经存在的数据类型。
Specialization
concept refinement使写出更多更好的算法成为可能,因为refine concept引入了更多的操作来描述更加丰富的抽象。多数情况下,这些附加的操作允许实现新的算法,比如说,BidirectionalIterator允许reverse()算法的高效实现。而且,refinement也允许某些算法使用refine concept得到更实用更高效的实现。
让我们考虑这个多边形concept。我们可以想象,这里有两个重要的操作:一个是num_sides(),它返回多边形的边数;另一个是side_length(i),它返回第i个边的长度。我们可以在线性时间内计算多边形的周长:
// 要求: Polygon<P>
template<typename P>
double circumference(P p) {
double result = 0;
for (int i = 0; i < num_sides(p); ++i)
result += side_length(p, i);
return result;
}
我们可以创建一个叫EquilateralPolygon (等边多边形)的concept,它refine了多边形concept,但它的所有边都有相同的长度。因此,我们就能够应用上面的circumference()算法到任何的EquilateralPolygon 上。但是,我们还能做得更好,因为可以使用下面的算法在常数时间内计算出EquilateralPolygon 的周长:
// 算法: EquilateralPolygon<P>
template<typename P>
double circumference(P p) {
return num_sides(p) * side_length(p, 0);
}
现在我们就有了两circumference()的实现,它们只是在要求是有一点不同。
GP要求这些实现的多数特征总应该被选择,这个特征常被称为concept-based overloading。比如,如果一个抽象是一个EquilateralPolygon,就应该使用常数时间的周长算法;相反,我们应该退回到线性时间的算法。在C++中,这个可以用一种称为tag dispatching的技术来实现。在这里我们就不详述了。
concept-based overloading确保总是使用最高效的算法实现。这种行为用来对付某些过度泛化的情况是非常有用的。过度法制化通常会导致算法更加通用,但非常低效。比如,标准模板库中的lower_bound()算法就有一个非常复杂微妙的条款:
比较的数量是对数的:大约在log(last-first) + 1。如果ForwardIterator是一个Random Access Iterator,那么遍历区间的步数也是对数的;否则步数与(last-first)成正比。
lower_bound()是一个二分法查找算法,但是它能够只用ForwardIterator来实现。这样就需要线性的查找时间,因为我们需要逐个查找序列中的元素。但是如果算法中是一个随机迭代器,它就能在序列中来回跳转,这样就只需要对数数量的步数了。在STL中,这是通过特化advance()和distance()函数来实现的,前者用来向前移动一定数量的步数,后者则计算两个迭代器之间的距离。通过使用这些公用算法,STL就能lift lower_bound()算法,只它从一个要求随机迭代器的算法特化成只需要一个ForwardIterator的算法,却不需要牺牲在随机迭代器情况下的性能。
结论
这个简介已经介绍了全部的GP过程,从用concept分析最初的lift具体实现为泛型算法,通过model来映射不同的抽象到concept,以及最后使用特化来为更加具体的concept提供改进的算法。关于GP还有更多的勤工东西方需要学习。下面的参考提供了更多关于GP的消息来源,或者看一些泛型库的代码来做进一步的学习。
| |||




















 131
131

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








