设计循环队列

原创已于 2025-12-15 20:38:52 修改 · 853 阅读

6 ·

CC 4.0 BY-SA版权

文章标签：

#链表 #数据结构

于 2025-12-15 20:11:07 首次发布

数据结构专栏收录该内容

6 篇文章

订阅专栏

https://leetcode.cn/problems/design-circular-queue/

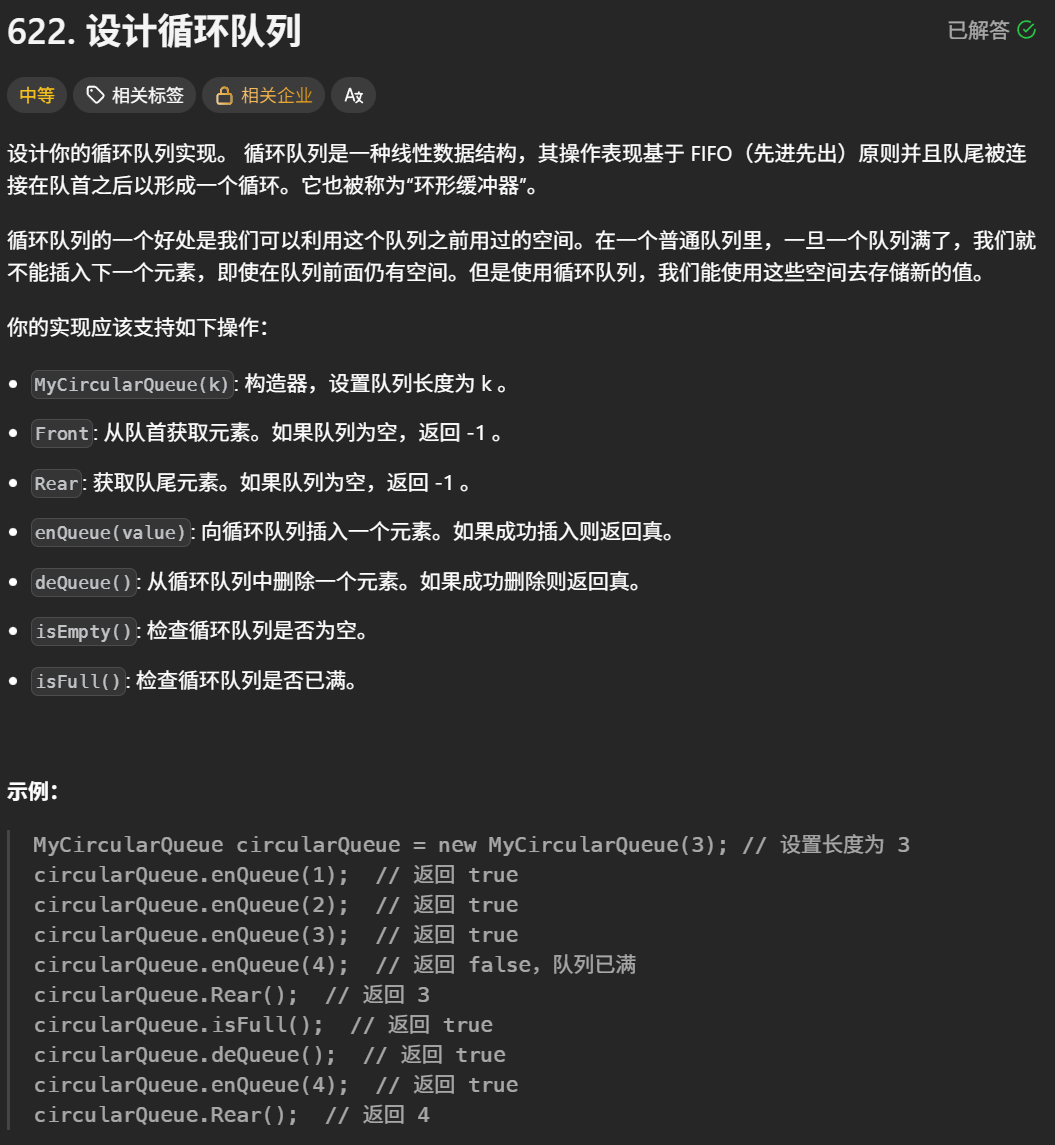
题目要求

class MyCircularQueue {
public:
    MyCircularQueue(int k) {
        
    }
    
    bool enQueue(int value) {
        
    }
    
    bool deQueue() {
        
    }
    
    int Front() {
        
    }
    
    int Rear() {
        
    }
    
    bool isEmpty() {
        
    }
    
    bool isFull() {
        
    }
};

/**
 * Your MyCircularQueue object will be instantiated and called as such:
 * MyCircularQueue* obj = new MyCircularQueue(k);
 * bool param_1 = obj->enQueue(value);
 * bool param_2 = obj->deQueue();
 * int param_3 = obj->Front();
 * int param_4 = obj->Rear();
 * bool param_5 = obj->isEmpty();
 * bool param_6 = obj->isFull();
 */

思路

链表和数组的选择

先读一下题，这个题要求我们实现一个“循环队列”，这个循环队列和普通队列的区别在于

1、队列的长度是一定的

2、队列中的空间是可以被重复利用的

我们这里有两种实现的思路，一种是通过数组，一种是通过链表。

好像乍一看上去是使用链表好做一点

实则不然，如果我们使用链表，链表的结点数量肯定是固定的，这时候，我们想要知道链表是否满了就是一个问题，我们怕不是得将每一个链表节点都安排一个flag来标注这个节点是不是满的，在判空和判满的时候也得将全部的节点都遍历一遍，这实际上是很浪费时间和空间的。

所以我们这里还是使用数组来完成这一道题

基本变量的声明

要实现找到头和尾的效果，我们一定得有两个“指针”（这里其实是数字）分别指向head和tail

这里又有一个问题：我们的tail应该指向那里？是下一个节点还是当前最后一个有效节点

别忘了我们这里使用的是数组，我们如果使用的是指向最后一个有效节点的话，在初始化的时候，我们就得将tail设置为-1了，显然：-1在数组中的使用是有一点难绷的

所以我们这里采用tail设置为最后一个有效元素的下一个元素的方案

我们可以看到在题目中给到的函数中并没有给我们k的接口，我们还是将k作为一个成员变量比较好

 private:
    int _head;
    int _tail;
    int _k;
    int* arr;

问题：如何判满和判空

空的时候自不必说，肯定是head==tail

但是满的情况又该如何判断呢？

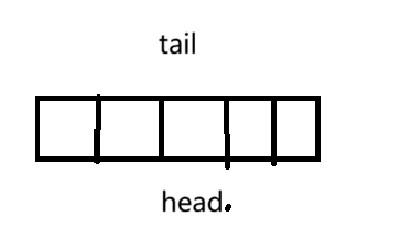
此时，tail已经转了一圈回来了，这个队列肯定是满的，但是表现还是tail==head，我们没法区分到底是满的还是空的。

这里有两种方案：

1、引入一个size来记录现在的有效数据个数

2、多开一个“影子节点”，并保持数组中永远有一个节点是没有存数据的

第一种方案是很好实现的，我在此不过多讲述

我们着重讲第二种方案

因为我们数组中永远有一个空间是没有存数据的，只要tail指向的下一个节点是head就可以认为此时队列是满的

如图所示，这种情况就是满的

我们在为队列开辟空间的时候多开辟一个空间

 MyCircularQueue(int k) 
    {
        arr=(int*)malloc(sizeof(int)*(k+1));
        _k=k;
        _head=0;
        _tail=0;   
    }

那我问你：这种情况怎么办

这就引出一个回转问题了

回转问题

我们使用的head和tail在使用的过程中都会有到了结尾的位置的情况，此时如果不回转到开始的位置的话，多少是有一点棘手的。

我们这时只需要在head和tail移动时%一个(k+1)即可

因为，当移动后的数字小于(k+1)时，%（k+1）也没有什么影响

当移动后的数字大于等于（k+1）时，%（k+1）就可以将数字返回到开头的位置，从而实现数字的回转

实现

初始化

 MyCircularQueue(int k) 
    {
        arr=(int*)malloc(sizeof(int)*(k+1));
        _k=k;
        _head=0;
        _tail=0;   
    }

判空和判满

bool isEmpty() {
        return _head==_tail;
    }
    
    bool isFull() {
        return (_tail+1)%(_k+1)==_head;
    }

读取首尾

 int Front() {
        if(isEmpty())
        return -1;
        else
        {
            return arr[_head];
        }
    }
    
    int Rear() {
        if(isEmpty())
        return -1;
        else
        {
            return arr[(_tail+_k+1-1)%(_k+1)];
            //这里是一个非常有意思的小点
        }
    }

这里有一个需要注意的小点：

return arr[(_tail+_k+1-1)%(_k+1)];

我们的_tail指向的是最后一个有效数字的下一个节点，我们返回的一定是他的上一个节点

这里(_tail-1+k+1)%(k+1)在tail大于0的时候都是不会产生什么影响的（两个(k+1)直接约了），但是在tail等于零的时候用处就大了，可以实现跳到上一个有效数字的效果。

出数据和入数据

 bool enQueue(int value) {
        if(isFull())
        return false;
        else
        {
            arr[_tail]=value;
            _tail=(_tail+1)%(_k+1);
            return true;
        }
    }
    
    bool deQueue() 
    {
        if(isEmpty())
        return false;
        else
        {
            _head=(_head+1)%(_k+1);
            return true;
        }   
    }

总代码

class MyCircularQueue {
    private:
    int _head;
    int _tail;
    int _k;
    int* arr;
public:
    MyCircularQueue(int k) 
    {
        arr=(int*)malloc(sizeof(int)*(k+1));
        _k=k;
        _head=0;
        _tail=0;   
    }
    
    bool enQueue(int value) {
        if(isFull())
        return false;
        else
        {
            arr[_tail]=value;
            _tail=(_tail+1)%(_k+1);
            return true;
        }
    }
    
    bool deQueue() 
    {
        if(isEmpty())
        return false;
        else
        {
            _head=(_head+1)%(_k+1);
            return true;
        }   
    }
    
    int Front() {
        if(isEmpty())
        return -1;
        else
        {
            return arr[_head];
        }
    }
    
    int Rear() {
        if(isEmpty())
        return -1;
        else
        {
            return arr[(_tail+_k+1-1)%(_k+1)];
            //这里是一个非常有意思的小点
        }
    }
    
    bool isEmpty() {
        return _head==_tail;
    }
    
    bool isFull() {
        return (_tail+1)%(_k+1)==_head;
    }
};

/**
 * Your MyCircularQueue object will be instantiated and called as such:
 * MyCircularQueue* obj = new MyCircularQueue(k);
 * bool param_1 = obj->enQueue(value);
 * bool param_2 = obj->deQueue();
 * int param_3 = obj->Front();
 * int param_4 = obj->Rear();
 * bool param_5 = obj->isEmpty();
 * bool param_6 = obj->isFull();
 */