G1. 在 △ABC\triangle ABC△ABC 中, DDD, EEE, FFF 分别是 BCBCBC, ACACAC, ABABAB 三边上的旁切圆切点, ∠BAC\angle BAC∠BAC 的角平分线交 DEDEDE 于点 YYY, ∠BCA\angle BCA∠BCA 的角平分线交 EFEFEF 于点 XXX. 求证: XYXYXY 的中点在边 ACACAC 的垂直平分线上. (2025, 俄罗斯Tuymaada数学奥林匹克)
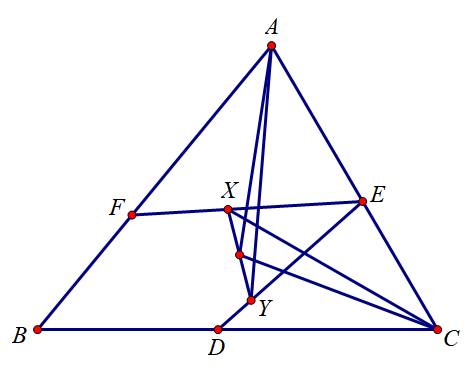
证明: 只需证明: AYcos(A/2)=CXcos(C/2)AY \cos(A/2)=CX \cos(C/2)AYcos(A/2)=CXcos(C/2), 即 AY/CX=cos(C/2)/cos(A/2)AY/CX=\cos(C/2)/\cos(A/2)AY/CX=cos(C/2)/cos(A/2).
设 YYY 到 ACACAC 的距离为 ddd, XXX 到 ACACAC 的距离为 d′d'd′.
AY/CX=(d/d′)⋅(sin(C/2)/sin(A/2))AY/CX=(d/d') \cdot (\sin (C/2)/\sin (A/2))AY/CX=(d/d′)⋅(sin(C/2)/sin(A/2)).
所以只需证明 d/d′=tan(A/2)/tan(C/2)d/d'=\tan(A/2)/\tan(C/2)d/d′=tan(A/2)/tan(C/2).
设 DYDYDY : YE=1−λYE=1-\lambdaYE=1−λ : λ\lambdaλ.
d(Yd(Yd(Y, AB)=(1−λ)d(DAB)=(1-\lambda)d(DAB)=(1−λ)d(D, AB)+(1−λ)d(EAB)+(1-\lambda)d(EAB)+(1−λ)d(E, AB)AB)AB).
d(Yd(Yd(Y, AC)=(1−λ)d(EAC)=(1-\lambda)d(EAC)=(1−λ)d(E, AC)AC)AC).
d(Dd(Dd(D, AB)=BDsinBAB)=BD \sin BAB)=BDsinB, d(Ed(Ed(E, AB)=AEsinAAB)=AE \sin AAB)=AEsinA, d(Ed(Ed(E, AC)=CDsinCAC)= CD \sin CAC)=CDsinC.
BDBDBD : AEAEAE : CD=1tan(C/2)CD=\frac{1}{\tan (C/2)}CD=tan(C/2)1 : 1tan(C/2)\frac{1}{\tan (C/2)}tan(C/2)1 : 1tan(B/2)\frac{1}{\tan (B/2)}tan(B/2)1.
sinB\sin BsinB :sinA\sin AsinA :sinC=a\sin C=asinC=a : bbb : ccc.
解得: λ=−atan(B/2)btan(B/2)−ctan(C/2)−atan(B/2)\lambda = \frac{-a\tan (B/2)}{b\tan (B/2)-c\tan (C/2)-a\tan (B/2)}λ=btan(B/2)−ctan(C/2)−atan(B/2)−atan(B/2).
进而 d=−asinCbtan(B/2)−ctan(C/2)−atan(B/2)d=\frac{-a\sin C}{b \tan (B/2)-c\tan (C/2)-a\tan (B/2)}d=btan(B/2)−ctan(C/2)−atan(B/2)−asinC.
类似地 (A(A(A, CCC 互换), 得到:
d′=−csinAbtan(B/2)−atan(A/2)−ctan(B/2)d'=\frac{-c\sin A}{b \tan (B/2)-a\tan (A/2)-c\tan (B/2)}d′=btan(B/2)−atan(A/2)−ctan(B/2)−csinA.
dd′=btan(B/2)−atan(A/2)−ctan(B/2)btan(B/2)−ctan(C/2)−atan(B/2)\frac{d}{d'} = \frac{b \tan (B/2)-a\tan (A/2)-c\tan (B/2)}{b \tan (B/2)-c\tan (C/2)-a\tan (B/2)}d′d=btan(B/2)−ctan(C/2)−atan(B/2)btan(B/2)−atan(A/2)−ctan(B/2).
dd′=tan(A/2)/tan(C/2)\frac{d}{d'}=\tan(A/2)/\tan(C/2)d′d=tan(A/2)/tan(C/2) 等价于
(b−a)tan(B/2)tan(A/2)+(c−b)tan(C/2)tan(B/2)+(a−c)tan(A/2)tan(C/2)=0(b-a) \tan(B/2)\tan (A/2) +(c-b)\tan(C/2)\tan(B/2)+(a-c)\tan(A/2)\tan(C/2)=0(b−a)tan(B/2)tan(A/2)+(c−b)tan(C/2)tan(B/2)+(a−c)tan(A/2)tan(C/2)=0.
左右同乘 cos(A/2)cos(B/2)cos(C/2)\cos(A/2)\cos(B/2)\cos(C/2)cos(A/2)cos(B/2)cos(C/2), 再经整理, 得到:
asinA(sin(C/2)cos(B/2)−sin(B/2)cos(C/2))+bsinB(sin(A/2)cos(C/2)−sin(C/2)cos(A/2))+csinC(sin(B/2)cos(A/2)−sin(A/2)cos(B/2))=0a\sin A (\sin (C/2)\cos(B/2)-\sin (B/2)\cos(C/2))+b\sin B (\sin (A/2)\cos(C/2)-\sin (C/2)\cos(A/2))+c\sin C (\sin (B/2)\cos(A/2)-\sin (A/2)\cos(B/2))=0asinA(sin(C/2)cos(B/2)−sin(B/2)cos(C/2))+bsinB(sin(A/2)cos(C/2)−sin(C/2)cos(A/2))+csinC(sin(B/2)cos(A/2)−sin(A/2)cos(B/2))=0.
进一步:
acosC+B2sinC−B2+bcosA+C2sinA−C2+ccosB+A2sinB−A2=0a \cos \frac{C+B}{2}\sin \frac{C-B}{2}+b \cos \frac{A+C}{2}\sin \frac{A-C}{2} + c \cos \frac{B+A}{2}\sin \frac{B-A}{2}=0acos2C+Bsin2C−B+bcos2A+Csin2A−C+ccos2B+Asin2B−A=0.
和差化积, 得到:
a(sinC−sinB)+b(sinA−sinC)+c(sinB−sinA)=0a(\sin C-\sin B)+b(\sin A-\sin C)+c(\sin B-\sin A)=0a(sinC−sinB)+b(sinA−sinC)+c(sinB−sinA)=0.
由正弦定理, a(sinC−sinB)+b(sinA−sinC)+c(sinB−sinA)=a(c−b)+b(a−c)+c(b−a)=0a(\sin C-\sin B)+b(\sin A-\sin C)+c(\sin B-\sin A)=a(c-b)+b(a-c)+c(b-a)=0a(sinC−sinB)+b(sinA−sinC)+c(sinB−sinA)=a(c−b)+b(a−c)+c(b−a)=0.
证毕.
G2. 在 △ABC\triangle ABC△ABC 中, XXX 为 (ABC)(ABC)(ABC) 的弧 BC⌢\overset{\LARGE{\frown}}{BC}BC⌢ 上的一动点, YYY, ZZZ 分别为射线 XCXCXC, XBXBXB 上的两个点, 使得 XA=XY=XZXA=XY=XZXA=XY=XZ. 求证: YZYZYZ 恒过定点. (2025, 俄罗斯Tuymaada数学奥林匹克)
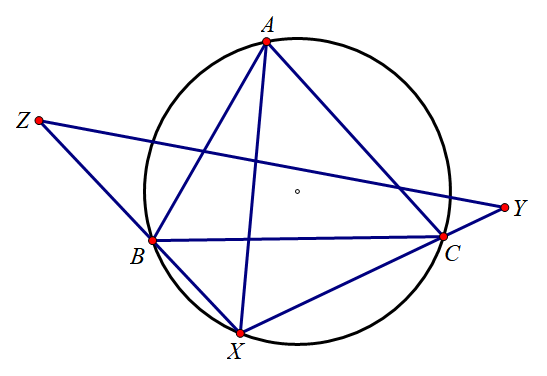
证明:
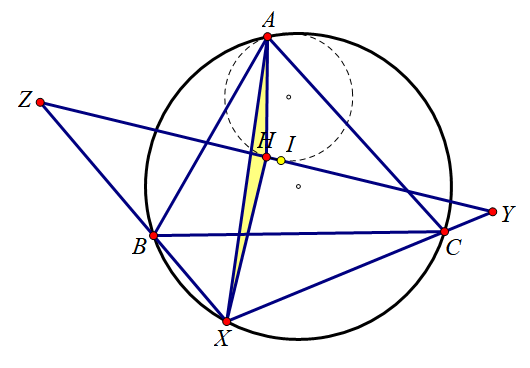
恒过 △ABC\triangle ABC△ABC 的内心(记为 III).
过 XXX 向 YZYZYZ 作垂线, 垂足记为 HHH.
HX/XA=HX/XY=cos∠BXC2HX/XA=HX/XY=\cos \frac{\angle BXC}{2}HX/XA=HX/XY=cos2∠BXC 为定值.
∠AXH=∣∠BXA−∠BXC2∣=∣∠BCA−∠BXC2∣\angle AXH = |\angle BXA-\frac{\angle BXC}{2}| = |\angle BCA-\frac{\angle BXC}{2}|∠AXH=∣∠BXA−2∠BXC∣=∣∠BCA−2∠BXC∣ 为定值.
所以 △AHX\triangle AHX△AHX 形状固定.
∠HAX\angle HAX∠HAX 大小固定, 且 HA/XAHA/XAHA/XA 是定值, 所以 HHH 的轨迹是缩放加旋转后的 XXX 的轨迹, 为一条定弧.
下面证明这条弧所在地圆过点 III.
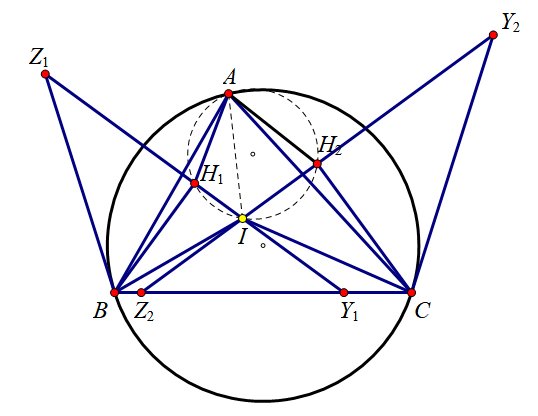
分别让 XXX 趋于 BBB 和 CCC.
XXX 趋于 BBB 时 YYY, ZZZ, HHH 的极限位置的记法在原基础上加以下标1, XXX 趋于 CCC 时加以下标2.
显然 BZ1BZ_1BZ1 和 CY2CY_2CY2 是 (ABC)(ABC)(ABC) 的切线.
显然 Y1Y_1Y1 是 AAA 关于 BIBIBI 的对称点.
∠IY1B=∠IAB=∠BAC2=∠H1Y1B\angle IY_1B=\angle IAB=\frac{\angle BAC}{2}=\angle H_1Y_1B∠IY1B=∠IAB=2∠BAC=∠H1Y1B.
所以 Y1Y_1Y1, III, H1H_1H1 三点共线.
类似地, Z2Z_2Z2, III, H2H_2H2 三点共线.
上述定弧所在的圆显然为 (AH1H2)(AH_1H_2)(AH1H2).
易知 ∠H1IH2=π−∠BAC\angle H_1IH_2 =\pi-\angle BAC∠H1IH2=π−∠BAC, 所以上述定弧也经过 III.
∠IHA=∠IH1A=π2\angle IHA=\angle IH_1A=\frac{\pi}{2}∠IHA=∠IH1A=2π, 所以 III 在 XYXYXY 上.
证毕.
G3. 在梯形 ABCDABCDABCD 中, MMM 是 ADADAD 中点, EEE 在线段 BMBMBM 上. 已知 ∠ADB=∠MAE=∠BMC\angle ADB=\angle MAE=\angle BMC∠ADB=∠MAE=∠BMC. 求证: △BCE\triangle BCE△BCE 是等腰三角形. (2021, 俄罗斯Tuymaada数学奥林匹克)
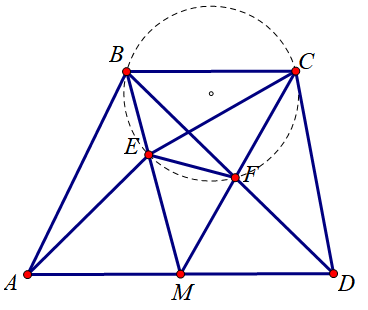
证明:
设 CMCMCM 与 BDBDBD 交于点 FFF.
∠EAM=∠BMC\angle EAM=\angle BMC∠EAM=∠BMC, ∠EMA=∠CBM\angle EMA=\angle CBM∠EMA=∠CBM, 所以 △EAM∼△CMB\triangle EAM \sim \triangle CMB△EAM∼△CMB.
EM=BC⋅(AM/BM)=BC⋅(MD/BM)EM=BC \cdot (AM/BM) = BC \cdot (MD/BM)EM=BC⋅(AM/BM)=BC⋅(MD/BM).
ME/MF=(BC/BM)⋅(MD/MF)ME/MF=(BC/BM) \cdot (MD/MF)ME/MF=(BC/BM)⋅(MD/MF).
其中 MD/MF=BC/CF=MC/BCMD/MF=BC/CF=MC/BCMD/MF=BC/CF=MC/BC.
所以 ME/MF=MC/BMME/MF=MC/BMME/MF=MC/BM
进而 △MEF∼△MCB\triangle MEF \sim \triangle MCB△MEF∼△MCB.
显然 BBB, EEE, FFF, CCC 四点共圆.
∠BEC=∠BFC=∠MBC\angle BEC=\angle BFC=\angle MBC∠BEC=∠BFC=∠MBC.
证毕.
G4. 已知△ABC\triangle ABC△ABC. 点DDD和EEE分别位于射线BCBCBC 和 ACACAC 上, 因此 BBB 位于 CCC 和 DDD, CCC 在 AAA 和 EEE 之间, BC=BDBC=BDBC=BD, ∠BAD=∠CDE\angle BAD= \angle CDE∠BAD=∠CDE. △ABC\triangle ABC△ABC 和 △ADE\triangle ADE△ADE 的周长之比为2. 求出这些三角形的面积. (2020, 俄罗斯Tuymaada数学奥林匹克)
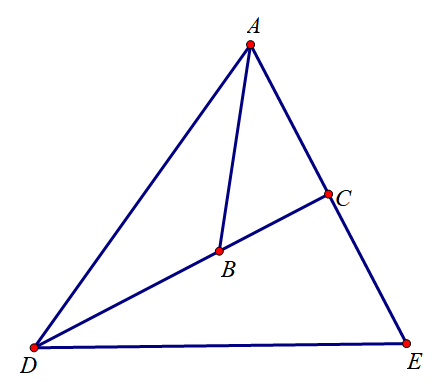
证明:
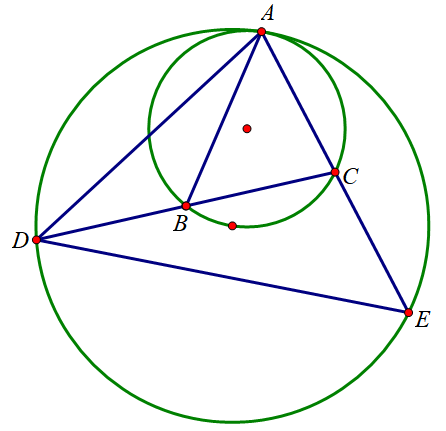
显然 ∠ABC=∠ADE\angle ABC=\angle ADE∠ABC=∠ADE, 结合 △ABC\triangle ABC△ABC 和 △ADE\triangle ADE△ADE 的外接圆半径之比是1/2可知 AE=2ACAE=2ACAE=2AC.
结合 BC=BDBC=BDBC=BD 可知 S△ABC/S△ADE=4S_{\triangle ABC} / S_{\triangle ADE}=4S△ABC/S△ADE=4.





















 1441
1441

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








