机器学习实践—基于Scikit-Learn、Keras和TensorFlow2第二版—第11章训练深度神经网络

训练深度神经网络并非易事，常常会遇到如下问题：

梯度消失和爆炸问题，导致神经网络前面的层无法得到很好地训练
数据不足，或者标注代价太大
训练速度极慢
参数较多时很容易过拟合，尤其是在数据量不足或数据存在大师噪声时

0. 导入所需的库

import tensorflow as tf
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
%matplotlib inline
import os

for i in (tf, np, mpl):
    print(i.__name__,": ",i.__version__,sep="")

输出：

tensorflow: 2.2.0
numpy: 1.17.4
matplotlib: 3.1.2

1. 梯度消失和梯度爆炸问题

1.1 梯度消失和梯度爆炸

梯度消失：梯度通过梯度下降算法反向传播时越来越小，导致前面的网络层无法很好地收敛。

梯度爆炸：梯度在传播过程中不断变大，使得权重更新幅度太小而导致发散，无法收敛。通常在循环神经网络中比较严重。

这些问题很早之前就有发现，并且是2000年代初期神经网络被冷漠的原因之一。

2010年Xavier Glorot和Yoshua Bengio发表的文章指出这些问题存在的原因：使用了Sigmoid激活函数、均值为0方差为1的权重初始化方法。因为随着神经网络前向传播，加权求和的结果的绝对值越来越大，再经过Sigmoid函数时，结果越来越接近1或0，此时的平均值大约是0.5，而不是0。因此双曲正切tanh函数在这方面可能效果会更好。

def logit(x):
    return 1/(1+np.exp(-x))

z = np.linspace(-5, 5, 200)

plt.plot([-5, 5], [0, 0], 'k-')
plt.plot([-5, 5], [1, 1], 'k--')
plt.plot([0, 0], [-0.2, 1.2], 'k-')
plt.plot([-5, 5], [-3/4, 7/4], 'g--')
plt.plot(z, logit(z), "b-", linewidth=2)
props = dict(facecolor='black', shrink=0.1)
plt.annotate('Saturating', xytext=(3.5, 0.7), xy=(5, 1), arrowprops=props, fontsize=14, ha="center")
plt.annotate('Saturating', xytext=(-3.5, 0.3), xy=(-5, 0), arrowprops=props, fontsize=14, ha="center")
plt.annotate('Linear', xytext=(2, 0.2), xy=(0, 0.5), arrowprops=props, fontsize=14, ha="center")
plt.grid(True)
plt.title("Sigmoid activation function", fontsize=14)
plt.axis([-5, 5, -0.2, 1.2])

plt.show()

输出：

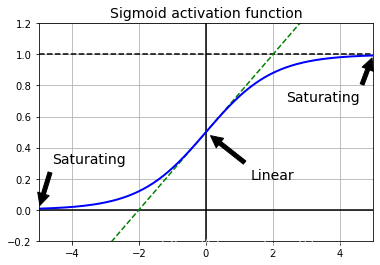
如上图所示为Sigmoid函数图像，当输入>4或<-4时函数值基本接近于0或者1，也就是说饱和了，而此时导数就接近于0，因此这种情况反向传播就会出现梯度消失的问题。

1.2 Glorot and He初始化(Xavier and He Initialization, Glorot and He Initialization)

Glorot和Bengio在其文章是指出，神经网络期望是输入方差和输出方差相等，梯度前向和向后的方差也相等，但这是不可能的，除非保证每次的输入和神经元数目相等。但是他们提出的一个折中的办法，当使用如Sigmoid类似的logistic函数时，权重的初始化使用如下的随机初始化方法：

初始化方法一：采用均值为0，方差为 $\frac{1}{fan_{avg}}$ 的正态分布
初始化方法二：采用-r到r的均匀分布

其中：

$fan_{avg} = \frac{fan_{in}+fan_{out}}{2}$

$r = \sqrt{\frac{3}{fan_{avg}}}$

以上这两种初始化叫做Xavier初始化或者Glorot初始化。

如果将上式中的 $fan_{avg}$ 换成 $fan_{in}$ 就成了LeCun于1990年提出的初始化方法。当 $fan_{in} = fan_{out}$ 时，LeCun初始化方法等价于Glorot初始化方法。

研究人员花了十多年才发现这些规律，使用Glorot初始化方法可以大大加速训练速度，并且这也是深度学习成功的原因之一。

针对ReLU激活函数（包括ELU等变体）的初始化方法叫He初始化方法，即文章的第一作者何恺明，详细论文请看：Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification（https://arxiv.org/abs/1502.01852）

SELU激活函数使用LeCun初始化方法。

在Keras中，默认使用Glorot初始化方法中的均匀分布方法。在Keras中可以通过kernel_initializer指定为其它初始化方法。

[name for name in dir(tf.keras.initializers) if not name.startswith("_")]

输出：

['Constant',
 'GlorotNormal',
 'GlorotUniform',
 'Identity',
 'Initializer',
 'Ones',
 'Orthogonal',
 'RandomNormal',
 'RandomUniform',
 'TruncatedNormal',
 'VarianceScaling',
 'Zeros',
 'constant',
 'deserialize',
 'get',
 'glorot_normal',
 'glorot_uniform',
 'he_normal',
 'he_uniform',
 'identity',
 'lecun_normal',
 'lecun_uniform',
 'ones',
 'orthogonal',
 'serialize',
 'zeros']

如上输出所示为Keras中可以使用的所有初始化方法。

tf.keras.layers.Dense(10, activation="relu",kernel_initializer="he_normal")

输出：

<tensorflow.python.keras.layers.core.Dense at 0x1da88f60>

如上代码表示，使用ReLU激活函数，并使用he初始化方法的正态分布初始化。

init = tf.keras.initializers.VarianceScaling(scale=2.0, mode="fan_avg",distribution="uniform")
tf.keras.layers.Dense(10, activation="relu", kernel_initializer=init)

输出：

<tensorflow.python.keras.layers.core.Dense at 0x1db5c978>

如上输出所示为使用ReLU激活函数，并在使用he初始化时基于fan_avg的均匀分布。

1.3 非饱和激活函数(Nonsaturating Activation Functions)

上面提到的当使用Sigmoid函数时，使用Glorot初始化时不错的选择。但是ReLU激活函数在神经网络中表示出色，ReLU不会出现饱和的情况，同时计算梯度非常简单、快速。

但是，ReLU也有缺点，即dying ReLUs，主要观点是当输入小时0时，输出为0，因此在神经网络中可能导致某些神经元的输出为0，导致梯度也为0。

Leaky ReLU、RReLU和PReLU

为了解决如上缺点，提出了leaky ReLU，函数表达式如下：

𝐿𝑒𝑎𝑘𝑅𝑒𝐿𝑈𝛼(𝑥)=𝑚𝑎𝑥(𝛼𝑥,𝑥)

其中：

𝛼：表示输入x小于0时的直线斜率，通常设置为0.01

LeakyReLU防止了神经元死亡(die)的发生。

Bing Xu等2015年的研究(Empirical Evaluation of Rectified Activations in Convolutional Network, https://arxiv.org/abs/1505.00853)表明，leaky版本的ReLU效果往往比原生的ReLU效果要好。他们还研究了随机leakyReLU(RReLU)，即alpha在训练时根据给定范围随机选择，在测试时使用平均值。RReLU效果也不错，并且也可以作为一种防止过拟合的正则化手段。同时他们还研究了参数化leaky ReLU(PReLU)，即alpha作为可以训练的参数而不是指定的超参数，PReLU在大型图像数据集上效果完胜原生ReLU，但在小型数据集上有过拟合的风险。

很遗憾，RReLU在Keras中还没有实现。

def leaky_relu(x, alpha=0.01):
    return np.maximum(alpha*x, x)

plt.plot(z, leaky_relu(z, 0.05), "b-", linewidth=2)
plt.plot([-5, 5], [0, 0], 'k-')
plt.plot([0, 0], [-0.5, 4.2], 'k-')
plt.grid(True)
props = dict(facecolor='black', shrink=0.1)
plt.annotate('Leak', xytext=(-3.5, 0.5), xy=(-5, -0.2), arrowprops=props, fontsize=14, ha="center")
plt.title("Leaky ReLU activation function", fontsize=14)
plt.axis([-5, 5, -0.5, 4.2])

plt.show()

输出：

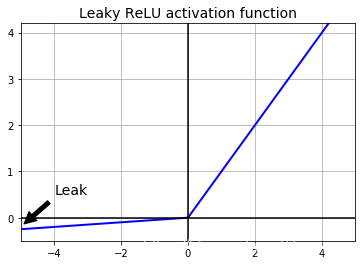
如上输出所示为alpha=0.01的leaky ReLU图像。

[m for m in dir(tf.keras.activations) if not m.startswith("_")]

输出：

['deserialize',
 'elu',
 'exponential',
 'get',
 'hard_sigmoid',
 'linear',
 'relu',
 'selu',
 'serialize',
 'sigmoid',
 'softmax',
 'softplus',
 'softsign',
 'swish',
 'tanh']

如上输出所示为Keras中所有可以使用的激活函数。

[m for m in dir(tf.keras.layers) if "relu" in m.lower()]

输出：

['LeakyReLU', 'PReLU', 'ReLU', 'ThresholdedReLU']

下面例子使用Leaky ReLU训练Fashion MNIST神经网络：

(X_train_full, y_train_full), (X_test, y_test) = tf.keras.datasets.fashion_mnist.load_data()
X_train_full = X_train_full / 255.0
X_test = X_test / 255.0
X_valid, X_train = X_train_full[:5000], X_train_full[5000:]
y_valid, y_train = y_train_full[:5000], y_train_full[5000:]

tf.random.set_seed(42)
np.random.seed(42)

model = tf.keras.models.Sequential([
    tf.keras.layers.Flatten(input_shape=[28, 28]),
    tf.keras.layers.Dense(300, kernel_initializer="he_normal"),
    tf.keras.layers.LeakyReLU(),
    tf.keras.layers.Dense(100, kernel_initializer="he_normal"),
    tf.keras.layers.LeakyReLU(),
    tf.keras.layers.Dense(10, activation="softmax")
])

model.compile(loss="sparse_categorical_crossentropy",optimizer=tf.keras.optimizers.SGD(lr=1e-3),metrics=["accuracy"])

history = model.fit(X_train, y_train, epochs=10, validation_data=(X_valid, y_valid))

输出：

Epoch 1/10
1719/1719 [==============================] - 4s 2ms/step - loss: 1.2819 - accuracy: 0.6229 - val_loss: 0.8886 - val_accuracy: 0.7160
Epoch 2/10
1719/1719 [==============================] - 4s 2ms/step - loss: 0.7955 - accuracy: 0.7362 - val_loss: 0.7130 - val_accuracy: 0.7656
Epoch 3/10
1719/1719 [==============================] - 4s 2ms/step - loss: 0.6816 - accuracy: 0.7721 - val_loss: 0.6427 - val_accuracy: 0.7898
Epoch 4/10
1719/1719 [==============================] - 4s 2ms/step - loss: 0.6217 - accuracy: 0.7944 - val_loss: 0.5900 - val_accuracy: 0.8066
Epoch 5/10
1719/1719 [==============================] - 4s 2ms/step - loss: 0.5832 - accuracy: 0.8075 - val_loss: 0.5582 - val_accuracy: 0.8202
Epoch 6/10
1719/1719 [==============================] - 4s 2ms/step - loss: 0.5553 - accuracy: 0.8157 - val_loss: 0.5350 - val_accuracy: 0.8238
Epoch 7/10
1719/1719 [==============================] - 4s 2ms/step - loss: 0.5338 - accuracy: 0.8225 - val_loss: 0.5157 - val_accuracy: 0.8304
Epoch 8/10
1719/1719 [==============================] - 4s 2ms/step - loss: 0.5173 - accuracy: 0.8272 - val_loss: 0.5079 - val_accuracy: 0.8286
Epoch 9/10
1719/1719 [==============================] - 4s 2ms/step - loss: 0.5040 - accuracy: 0.8288 - val_loss: 0.4895 - val_accuracy: 0.8390
Epoch 10/10
1719/1719 [==============================] - 4s 2ms/step - loss: 0.4924 - accuracy: 0.8321 - val_loss: 0.4817 - val_accuracy: 0.8396

下面例子使用PReLU训练Fashion MNIST神经网络：

tf.random.set_seed(42)
np.random.seed(42)

model = tf.keras.models.Sequential([
    tf.keras.layers.Flatten(input_shape=[28, 28]),
    tf.keras.layers.Dense(300, kernel_initializer="he_normal"),
    tf.keras.layers.PReLU(),
    tf.keras.layers.Dense(100, kernel_initializer="he_normal"),
    tf.keras.layers.PReLU(),
    tf.keras.layers.Dense(10, activation="softmax")
])

model.compile(loss="sparse_categorical_crossentropy",optimizer=tf.keras.optimizers.SGD(lr=1e-3),metrics=["accuracy"])

history = model.fit(X_train, y_train, epochs=10,validation_data=(X_valid, y_valid))

输出：

Epoch 1/10
1719/1719 [==============================] - 4s 3ms/step - loss: 1.3461 - accuracy: 0.6209 - val_loss: 0.9255 - val_accuracy: 0.7186
Epoch 2/10
1719/1719 [==============================] - 4s 2ms/step - loss: 0.8197 - accuracy: 0.7355 - val_loss: 0.7305 - val_accuracy: 0.7630
Epoch 3/10
1719/1719 [==============================] - 4s 2ms/step - loss: 0.6966 - accuracy: 0.7694 - val_loss: 0.6565 - val_accuracy: 0.7880
Epoch 4/10
1719/1719 [==============================] - 4s 3ms/step - loss: 0.6331 - accuracy: 0.7909 - val_loss: 0.6003 - val_accuracy: 0.8050
Epoch 5/10
1719/1719 [==============================] - 4s 3ms/step - loss: 0.5917 - accuracy: 0.8057 - val_loss: 0.5656 - val_accuracy: 0.8178
Epoch 6/10
1719/1719 [==============================] - 4s 3ms/step - loss: 0.5618 - accuracy: 0.8134 - val_loss: 0.5406 - val_accuracy: 0.8236
Epoch 7/10
1719/1719 [==============================] - 4s 3ms/step - loss: 0.5390 - accuracy: 0.8205 - val_loss: 0.5196 - val_accuracy: 0.8314
Epoch 8/10
1719/1719 [==============================] - 4s 3ms/step - loss: 0.5213 - accuracy: 0.8258 - val_loss: 0.5113 - val_accuracy: 0.8316
Epoch 9/10
1719/1719 [==============================] - 4s 3ms/step - loss: 0.5070 - accuracy: 0.8288 - val_loss: 0.4916 - val_accuracy: 0.8378
Epoch 10/10
1719/1719 [==============================] - 4s 3ms/step - loss: 0.4945 - accuracy: 0.8316 - val_loss: 0.4826 - val_accuracy: 0.8396

ELU

由Djork-Arné Clevert等人在2015年发表的文章()提出了一种新的激活函数：ELU(exponential linear unit，指数线性单元)，其效果（包括训练时间、准确率）完胜所有版本的ReLU激活函数。其函数表达式如下：

$ELU_\alpha(x) = \left\{\begin{matrix} \alpha(exp(x)-1) &if: x<0 \\ x & if:x>=0 \end{matrix}\right.$

ELU与ReLU非常相似，但也有区别：

当输入x小于0时，输出-alpha到0之间的值。alpha定义为当输入x是一个非常大的负值时的输出，通常情况下可以设定为1
当输入x小于0时，梯度不再是0
当alpha=1时，x=0处时连续的，因此可以在0处加快梯度下降而不会发生反弹的现象。

def elu(x, alpha=1):
    return np.where(x<0, alpha*(np.exp(x)-1),x)

plt.plot(z, elu(z), "b-", linewidth=2)
plt.plot([-5, 5], [0, 0], 'k-')
plt.plot([-5, 5], [-1, -1], 'k--')
plt.plot([0, 0], [-2.2, 3.2], 'k-')
plt.grid(True)
plt.title(r"ELU activation function ($\alpha=1$)", fontsize=14)
plt.axis([-5, 5, -2.2, 3.2])

plt.show()

输出：

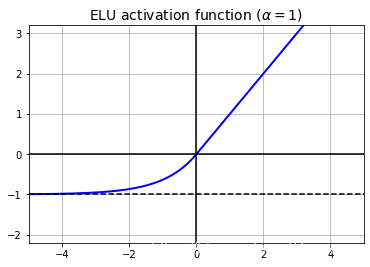
如上输出所示为alpha=1时的ELU函数图像。

ELU的缺点是计算速度比ReLU慢，因为如果输入小于0时需要计算指数，但是较快的收敛速度可以弥补这一点。而在测试时ELU就确实比ReLU慢。

SELU

Günter Klambauer等在2017年发表的文章(Self-Normalizing Neural Networks, https://arxiv.org/abs/1706.02515)提出了SELU(Scaled ELU)，即是一个ELU的变体。他们表示，如果一个神经网络只使用一些全连接层，并且这些全连接层全部使用SELU激活函数，那么这个网络就有自动归一化的功能，即最层的输出趋向于均值为0方差为1的分布，甚至是1000多层的网络也是如此，这便解决了梯度消失和爆炸的问题。对于在这种结构的神经网络上，SELU完胜其它版本的激活函数，尤其是特别深的网络。但是想要实现这种自动归一化的功能，也需要一些条件：

输入特征必须是均值为0方差为1
所有隐藏层权重使用LeCun正态分布初始化，例如在Keras设置为kernel_initializer="lecun_normal"
网络结构必须是连续性的，即全连接的，在其它结构的神经网络上效果没有其它激活函数好，例如循环网络等
该篇文章的作者只研究了所有层是全连接时具有很好的自动归一化功能，但其它研究者研究表明SELU激活函数在卷积神经网络上也表现很好。

然而在使用SELU的这种网络中，无法使用L1或L2正则化、dropout、max-norm、skip connections以及其它非连续拓扑结构

from scipy.special import erfc

z = np.linspace(-5, 5, 200)

# alpha and scale to self normalize with mean 0 and standard deviation 1
alpha_0_1 = -np.sqrt(2 / np.pi) / (erfc(1/np.sqrt(2)) * np.exp(1/2) - 1)
scale_0_1 = (1 - erfc(1 / np.sqrt(2)) * np.sqrt(np.e)) * np.sqrt(2 * np.pi) * (2 * erfc(np.sqrt(2))*np.e**2 + np.pi*erfc(1/np.sqrt(2))**2*np.e - 2*(2+np.pi)*erfc(1/np.sqrt(2))*np.sqrt(np.e)+np.pi+2)**(-1/2)

def selu(x, scale=scale_0_1, alpha=alpha_0_1):
    return scale * elu(x, alpha)

plt.plot(z, selu(z), "b-", linewidth=2)
plt.plot([-5, 5], [0, 0], 'k-')
plt.plot([-5, 5], [-1.758, -1.758], 'k--')
plt.plot([0, 0], [-2.2, 3.2], 'k-')
plt.grid(True)
plt.title("SELU activation function", fontsize=14)
plt.axis([-5, 5, -2.2, 3.2])

plt.show()

输出：

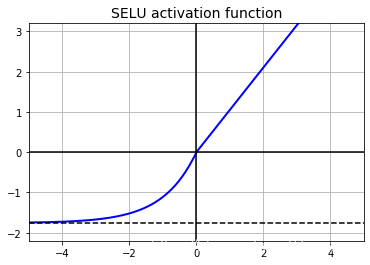
np.random.seed(42)
Z = np.random.normal(size=(500, 100)) # standardized inputs
for layer in range(1000):
    W = np.random.normal(size=(100, 100), scale=np.sqrt(1 / 100)) # LeCun initialization
    Z = selu(np.dot(Z, W))
    means = np.mean(Z, axis=0).mean()
    stds = np.std(Z, axis=0).mean()
    if layer % 100 == 0:
        print("Layer {}: mean {:.2f}, std deviation {:.2f}".format(layer, means, stds))

输出：

Layer 0: mean -0.00, std deviation 1.00
Layer 100: mean 0.02, std deviation 0.96
Layer 200: mean 0.01, std deviation 0.90
Layer 300: mean -0.02, std deviation 0.92
Layer 400: mean 0.05, std deviation 0.89
Layer 500: mean 0.01, std deviation 0.93
Layer 600: mean 0.02, std deviation 0.92
Layer 700: mean -0.02, std deviation 0.90
Layer 800: mean 0.05, std deviation 0.83
Layer 900: mean 0.02, std deviation 1.00

以上输出所示，每次的输出结果都基本为均值为0方差为1的分布。

下面例子使用SELU利用Fashion MNIST数据集训练100个隐藏层的神经网络，注意输入数据需要归一化：

np.random.seed(42)
tf.random.set_seed(42)

model = tf.keras.models.Sequential()
model.add(tf.keras.layers.Flatten(input_shape=[28, 28]))
model.add(tf.keras.layers.Dense(300, activation="selu",kernel_initializer="lecun_normal"))

for layer in range(99):
    model.add(tf.keras.layers.Dense(100, activation="selu",kernel_initializer="lecun_normal"))

model.add(tf.keras.layers.Dense(10, activation="softmax"))

model.compile(loss="sparse_categorical_crossentropy",optimizer=tf.keras.optimizers.SGD(learning_rate=1e-3),metrics=["accuracy"])

# 归一化
pixel_means = X_train.mean(axis=0, keepdims=True)
pixel_stds = X_train.std(axis=0, keepdims=True)
X_train_scaled = (X_train - pixel_means) / pixel_stds
X_valid_scaled = (X_valid - pixel_means) / pixel_stds
X_test_scaled = (X_test - pixel_means) / pixel_stds

history = model.fit(X_train_scaled, y_train, epochs=5,validation_data=(X_valid_scaled, y_valid))

输出：

Epoch 1/5
1719/1719 [==============================] - 31s 18ms/step - loss: 1.0580 - accuracy: 0.5978 - val_loss: 0.6905 - val_accuracy: 0.7422
Epoch 2/5
1719/1719 [==============================] - 31s 18ms/step - loss: 0.6646 - accuracy: 0.7588 - val_loss: 0.5594 - val_accuracy: 0.8112
Epoch 3/5
1719/1719 [==============================] - 31s 18ms/step - loss: 0.5790 - accuracy: 0.7971 - val_loss: 0.5434 - val_accuracy: 0.8112
Epoch 4/5
1719/1719 [==============================] - 31s 18ms/step - loss: 0.5211 - accuracy: 0.8221 - val_loss: 0.4808 - val_accuracy: 0.8370
Epoch 5/5
1719/1719 [==============================] - 31s 18ms/step - loss: 0.5105 - accuracy: 0.8245 - val_loss: 0.5023 - val_accuracy: 0.8258

再尝试使用ReLU方法：

np.random.seed(42)
tf.random.set_seed(42)

model = tf.keras.models.Sequential()
model.add(tf.keras.layers.Flatten(input_shape=[28, 28]))
model.add(tf.keras.layers.Dense(300, activation="relu", kernel_initializer="he_normal"))

for layer in range(99):
    model.add(tf.keras.layers.Dense(100, activation="relu", kernel_initializer="he_normal"))

model.add(tf.keras.layers.Dense(10, activation="softmax"))

model.compile(loss="sparse_categorical_crossentropy",optimizer=tf.keras.optimizers.SGD(learning_rate=1e-3),metrics=["accuracy"])

history = model.fit(X_train_scaled, y_train, epochs=5, validation_data=(X_valid_scaled, y_valid))

输出：

Epoch 1/5
1719/1719 [==============================] - 32s 18ms/step - loss: 1.7799 - accuracy: 0.2701 - val_loss: 1.3950 - val_accuracy: 0.3578
Epoch 2/5
1719/1719 [==============================] - 31s 18ms/step - loss: 1.1989 - accuracy: 0.4928 - val_loss: 1.1368 - val_accuracy: 0.5300
Epoch 3/5
1719/1719 [==============================] - 31s 18ms/step - loss: 0.9704 - accuracy: 0.6159 - val_loss: 1.0297 - val_accuracy: 0.6104
Epoch 4/5
1719/1719 [==============================] - 31s 18ms/step - loss: 2.0043 - accuracy: 0.2796 - val_loss: 2.0500 - val_accuracy: 0.2606
Epoch 5/5
1719/1719 [==============================] - 31s 18ms/step - loss: 1.5996 - accuracy: 0.3725 - val_loss: 1.4712 - val_accuracy: 0.3778

对比SELU和ReLU的结果发现，SELU的结果似乎远远好于ReLU的结果。

因此，神经网络隐藏层到底使用哪个激活函数呢？

通常情况下，优先选择排序为：SELU、ELU、leaky ReLU及其变体、ReLU、tanh、logistic。
如果网络的架构不支持自动归一化，能ELU效果可能会比SELU好。
如果非常关注模型运行时的时间，则应该首先leaky ReLU。如果不想调整其它任何超参数，则使用Keras中alpha=0.3的默认值。
如果时间和计算力充足，可以尝试交叉验证选择更好的激活函数，例如模型过拟合时选择RReLU，如果数据集特别大时选择PReLU。
由于目前最火的激活函数还是ReLU，因此很多库和硬件加速器都对ReLU类似的激活函数进行了优化，如果想要速度更快，那么ReLU还是最佳的选择。

1.4 批归一化(Batch Normalization)

虽然使用He初始化和ELU(及ReLU的任何变体)都以很好地降低训练开始时梯度消失和爆炸的问题，但不能保证这些问题不会在训练一段时间时发生。

Sergey Ioffe和Christian Szegedy在2015年发表的文章(Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift, https://arxiv.org/abs/1502.03167)中提出一种叫做批归一化(Batch Normalization (BN))的技术，可以用来解决该问题。

该方法的主要思想是在每个隐藏层激活函数的前后加入一些操作，这些操作包括对输入进行0中心化和归一化，对输出分别利用两个参数微量进行scales和shifts。

如果在模型开始就加入了一个BN层，那么就不再需要对训练集进行归一化了。

模型预测时应该是单个样本，因此无法计算平均值和方差，解决方案之一是模型训练结束后利用全部数据再跑一遍模型，计算每个BN层的平均值和方差，这些平均值和方差就在模型预测时使用。

然而BN的一些实现工具中常常使用层的输入平均和方差的移动平均来估计这些最终统计值。这也是Keras中BatchNormalization层使用的方法。

因此，输出scale向量(gamma)和offset向量(beta)参数通过反向传播进行学习，最终输入平均向量(u)和最终输入标准差向量(sigma)通过指数移动平均进行估算。

Ioffe和Szegedy研究表明，BN能很大程度上提升深度神经网络的性能，在ImageNet分类任务上有很大的提升，梯度消失的问题得到了很好地控制，甚至是使用logistic或tanh激活函数也可以控制梯度消失的问题。并且这种网络对参数初始化也不太敏感。

使用BN的网络训练速度较慢，但它本身需要较少的迭代次数，因此可以抵消这种不足。

下面使用Keras实现BN层：

model = tf.keras.models.Sequential([
    tf.keras.layers.Flatten(input_shape=[28, 28]),
    tf.keras.layers.BatchNormalization(),
    tf.keras.layers.Dense(300, activation="relu"),
    tf.keras.layers.BatchNormalization(),
    tf.keras.layers.Dense(100, activation="relu"),
    tf.keras.layers.BatchNormalization(),
    tf.keras.layers.Dense(10, activation="softmax")
])

model.summary()

输出：

Model: "sequential_4"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
flatten_4 (Flatten)          (None, 784)               0         
_________________________________________________________________
batch_normalization (BatchNo (None, 784)               3136      
_________________________________________________________________
dense_210 (Dense)            (None, 300)               235500    
_________________________________________________________________
batch_normalization_1 (Batch (None, 300)               1200      
_________________________________________________________________
dense_211 (Dense)            (None, 100)               30100     
_________________________________________________________________
batch_normalization_2 (Batch (None, 100)               400       
_________________________________________________________________
dense_212 (Dense)            (None, 10)                1010      
=================================================================
Total params: 271,346
Trainable params: 268,978
Non-trainable params: 2,368
_________________________________________________________________

bn1 = model.layers[1]
[(var.name, var.trainable) for var in bn1.variables]

输出：

[('batch_normalization/gamma:0', True),
 ('batch_normalization/beta:0', True),
 ('batch_normalization/moving_mean:0', False),
 ('batch_normalization/moving_variance:0', False)]

如上输出所示，每个BN层对于每个输入有四个参数：gamma, beta, mu和sigma。mu和sigma是移动平均，不会被反向传播影响，因此是不可训练的，共有2368个。

bn1.updates

输出：

[<tf.Operation 'cond/Identity' type=Identity>,
 <tf.Operation 'cond_1/Identity' type=Identity>]