绪 论
一、多项式曲线拟合1.误差函数(error function)
假设存在一个训练数据集,其包含N个数据点,表示为{(x1,y1)…..,(xn,yn)},,我们的目标是通过训练这些数据集,找到对于新的x值可预测出其y值的函数。
现在我们假定我们拟合数据的函数为一个多项式函数,其为:
其中的二分之一是为了以后的求偏导的方便。有时候为了更加方便我们经常使用根均方误差(root-mean-square):
除以N可以确保我们能够以相同的基础对比不同大小的数据集,平方保证其与目标变量y使用相同规模和单位进行度量。
有时候我们通过训练得到一个非常复杂的模型,其对训练数据有非常好的拟合性,但是其对新数据的预测效果非常差,这种情况我们称之为过拟合(over-fitting)。针对于这种情况,又提出一个叫正则化的方法,其主要是在误差函数里加上一个惩罚项。
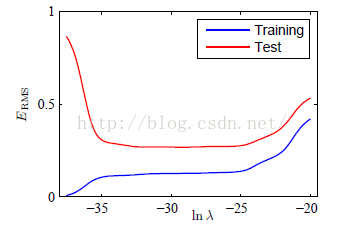
通过观察上面的式子,我们可以发现,如果我们的模型非常复杂,那么式子右边第一项将会非常小,但是第二项就会变得很大,反之则两项情况反过来,从而保证了平衡,当然我们如果能找到简单的模型能够对数据拟合的很好,从而第二项也很小,那是再好不过。R是常系数,对惩罚项有一定的平衡性,当其为0时,代价函数没有惩罚项。如图显示了均方根误差与lnr的关系。
1.离散事件和概率常识
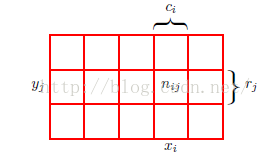
为了推导概率的规则,假设存在两个变量X和Y,X可以取任意的xi,Y可以取任意的yj。考虑进行N次实验,把出现xi的次数记为ci,出现yj的次数记为rj。那么出现xi的概率即为出现xi的次数(落在i单元格的点的个数)与N的比值,即:
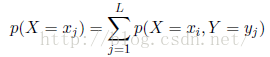
这是概率的加和规则(sum rule)有时也成p(X=xi)为边缘概率(marginal probability),因为它通过把其他的变量(如本例中的Y)边缘化或想家得到。进一步,如果我们只考虑X=xi的情况,那么在这之中Y=yj的概率记为p(Y=j|X=xi),它为给定的第i行中找到第j格的点数与第i行的总数比值,我们称之为给定X=xi的Y=yj的条件概率(condition probability),即为:
更进一步,我们从以上推导可以得到下面的关系:
这称之为概率的乘积规则。为了简介起见,,上面的两个结论可以表达为:
根据乘积规则,以及对称性p(X|Y ) = p(Y|X),我们立即得到了下面的两个条件概率之间的关系:
这被称为贝叶斯定理(Bayes' theorem),在模式识别和机器学习领域扮演着中心角色。使用加和规则,贝叶斯定理中的分母可以可以由如下计算而得:
以上我们简单讨论了离散事件的一些概率知识,现在我们来考虑与连续变量相关的概率。如果一个变量x落在区间(x,x+δx)的概率由p(x)δx表示(δx趋于0),那么p(x)称之为x的概率密度。x位于区间(a,b)上的概率为:
因为概率的非负的,并且x的值一定位于数轴上的某一个位置。所以概率密度满足:
假设存在一个变量的变化x=g(y),那么函数f(x)就变成了f1(g(y)),现在考虑一个概率密度px(x),它对应一个关于新变量y的密度py(y),对于很小的值,落在区间(x,x)内的观测转换为了区间(y,y),且px(x)=py(y),即:
上述的加和规则和乘积规则同样适用与概率密度函数的情形。,即为:
在概率分布为p(x)下函数f(x)的期望记为E(f),在离散分布中:
在连续变量的情形下,记为:
条件分布的期望为:
以上两种情形下,如果我们给定有限数量的N个点,这些点满足某个概率分布或者概率密度函数,那么期望可以通过求和的方式估计,即为:
方差定义为:
故方差也可以写为:
对于两个随机变量x和y,协方差定义为:
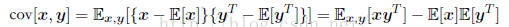
这里简单说明一下贝叶斯定理,根据我们之前的讨论以及乘积规则,假设多项式拟合的例子中存在参数w,那么在观测数据之前,其先验概率(prior probability)表示无p(w),假设观测数据为D={t1,...,tN},则条件概率为p(D|w),那么贝叶斯定律为:
贝叶斯定理右侧的量p(D|w)由观测数据集D来估计,可以被看成参数向量w的函数,被称为似然函数(likelihood function)。它表达了在不同的参数向量w下,观测数据出现的可能性的。注意,似然函数不是w的概率分布,并且它关于w的积分并不一定等于1。给定似然函数的定义,我们可以然语言表述贝叶斯定理:
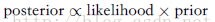
三、决策论
1.最小化误分类率和期望损失
我们总是希望分类得越准确越好,即误分类率越低越好。我们用一个规则来把每个x的值分到一个合适的类别,把输入空间切分成不同的区域Rk,这种区域被称为决策区域(decision region)。每个类别都有一个决策区域,区域Rk中的所有点都被分到Ck类。决策区域间的边界被叫做决策边界(decision boundary)或者决策面(decision surface)。那么一个错误的分类是指属于C1的类别划分到了C2中,其发生的概率为:
如果我们考虑分类的正确率的话,假设存在有K个类别,那么分类的正确率如下,并且我们将尽最大能力最大化其分类正确率。
在许多情形下,如果只用误差函数可能无法很好地表达出误差的损失,比如相对于把一个正常的人诊断为病人来说,把一个患病的人诊断为正常这种情况的代价是非常大的,因为很有可能让其错失治疗的机会。针对于这种情况,我们可以通过损失函数(loss function)来形式化地描述这个问题。损失函数也被称为代价函数(cost function)。假设对于新的x的值,真实的类别为Ck,我们把x分类为Cj(其中j可能与k相等,也可能不相等)。这样做的结果是,我们会造成某种程度的损失,记作Lkj,它可以看成损失矩(loss matrix)。对于一个给定的输入向量x,我们对于真实类别的不确定性通过联合概率分布p(x; Ck)表示。因此,我们转而去求最小化平均损失。平均损失根据这个联合概率分布计算,定义为:
最小化期望损失的决策规则是对于每个新的x,把它分到能使下式取得最小值的第j类:
2.推理和决策、回归问题的损失函数
在我们之前的讨论中,根据训练数据集可以得到关于p(Ck|x)的模型,根据其大小我们判断其类别。即通过学习一个函数,将输入x直接映射为决策。这样的函数被称为判别函数(discriminant function)。在应用中一共有三种方法求得,分别按照复杂度降低的顺序给出:
(1)根据贝叶斯定理,即:
其分母通过以下方法求得:
(2)首先解决确定后验类密度p(Ck j x)这一推断问题,接下来使用决策论来对新的输入x进行分类。这种直接对后验概率建模的方法法被称为判别式模型(discriminative models。
(3)找到一个函数f(x),被称为判别函数。这个函数把每个输入x直接映射为类别标签。例如,在二分类问题中,f()可能是一个二元的数值,f = 0表示类别C1,f = 1表示类别C2。这种情况下,概率不起作用。
接下来讨论以下分类问题。我们对于预测之后造成了一个个损失L(t; y(x))。平均损失(或者说期望损失)定义为:
在回归问题中,损失函数的一个通常的选择是平方损失,期望损失函数为:
采用变分法和概率的加和规则和乘积规则,可以得到:
这是在x的条件下t的条件均值,被称为回归函数(regression function)。我们也可以采用另外一种方法推得以上结论,先把平方项展开,即:
另外平方损失函数的一种推广叫做闵可夫斯基损失函数(Minkowski loss),它的期望为:
很明显看出当q = 2时,这个函数就变成了平方损失函数的期望。
四、信息论
1.基本介绍
假设一个发送者想传输一个随机变量的值给接收者。这个过程中,他们传输的平均信息量通可以通过求下面公式关于概率分布p(x)的期望得到。这个期望值为:
这个重要的量被叫做随机变量x的熵(entropy)。
在离散随机变量中,随机变量X的熵为:
在概率归一化的限制下,使用拉格朗日乘数法可以找到熵的最大值。因此,我们要最大化
我们可以把熵的定义扩展到连续变量x的概率分布p(x),方法如下。先先把x切分成宽度为Δ的箱子。然后假设p(x)是连续的。均值定理(mean value theorem)(Weisstein, 1999)告诉我们,对于每个这样的箱子,一定存在一个值xi使得:
我们现在可以这样量化连续变量x:只要x落在第i个箱子中,我们就把x赋值为xi。因此观察到值xi的概率为p(xi)Δ。这就变成了离散的分布,这种情形下熵的形式为:
我们看到,熵的离散形式与连续形式的差是lnΔ,这在极限Δ !趋于0的情形下发散。这反映出一个事实:具体化一个连续变量需要大量的比特位。对于定义在多元连续变量(联合起来记作向量x)上的概率密度,微分熵为:
在离散分布的情况下,我们看到最大熵对应于变量的所有可能状态的均匀分布。现在让我们考虑连续变量的最大熵。为了让这个最⼤大值有一个合理的定义,有必要限制p(x)的一阶矩和二阶矩,同时还要保留归一化的限制。因此我们最大化微分熵的时候要遵循下面三个限制:
假设我们有一个联合概率分布p(x; y)。我们从这个概率分布中抽取了⼀对x和y。如果x的值已知,那么需要确定对应的y值所需的附加的信息就是ln p(y|x)。因此,用来确定y值的平均附加信息可以写成:
条件熵满足下面的的关系:
2.相对熵和互信息
考虑某个未知的分布p(x),假定我们已经使用一个近似的分布q(x)对它进行了建模。如果我们使用q(x)来建立一个编码体系,用来把x的值传给接收者,那么,由于我们使用了q(x)而不是真实分布p(x),因此在具体化x的值(假定我们选择了一个有效的编码系统)时,我们需要一些附加的信息。我们需要的平均的附加信息量(单位是nat)为:
这被称为分布p(x)和分布q(x)之间的相对熵(relative entropy) 或者Kullback-Leibler散度(Kullback-Leibler divergence),或者KL散度(Kullback and Leibler,1951)。注意这不是一个对称量。如果一个函数具有如下性质:每条弦都位于函数图像或其上方(如图所示),那么我们说这个函数是凸函数。位于x = a到x = b之间的任何一个x值都可以写成λa + (1-λ)b的形式,其中λ大于等于0,小于等于1。弦上的对应点可以写成λf(a)+ (1-λ )f(b),函数的对应值为f(λa +(1-λ)b)。这样,凸函数的性质就可以表表示为:
显然,如果f(x)是凸函数,那么-f(x)就是凹函数。使用归纳法,我们可以得到凸函数f(x)满足:
现在考虑由p(x,y)给出的两个变量x和y组成的数据集。如果变量的集合是独⽴的,那么他们的联合分布可以分解为边缘分布的乘积p(x, y) = p(x)p(y)。如果变量不是独立的,那么我们可以通过考察联合概率分布与边缘概率分布乘积之间的Kullback-Leibler散度来判断它们是否“接近”于相互独立。此时,Kullback-Leibler散度为:
这被称为变量x和变量y之间的互信息(mutual information)。根据Kullback-Leibler散度的性质,我们看到I[x|y] 大于等于0,当且仅当x和y相互独立时等号成立。使用概率的加和规则和乘积规则,我们看到互信息和条件熵之间的关系为:
因此我们可以把互信息看成由于知道y值⽽造成的x的不确定性的减小(反之亦然)。从贝叶斯的观点来看,我们可以把p(x)看成x的先验概率分布,把p(x| y)看成我们观察到新数据y之后的后验概率分布。因此互信息表示一个新的观测y造成的x的不确定性的减小。








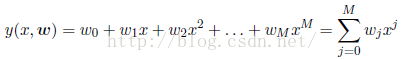
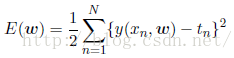
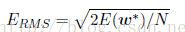
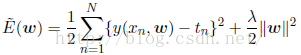
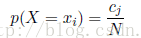
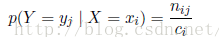
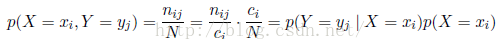
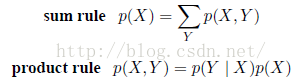
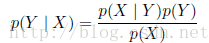
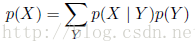
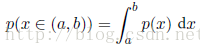
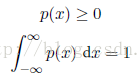
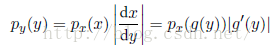
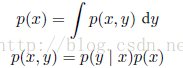
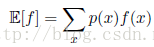

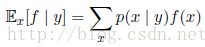
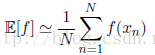
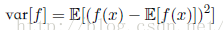
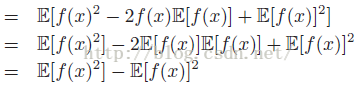
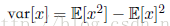
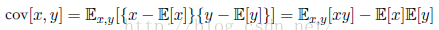
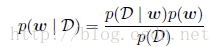
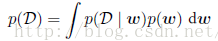
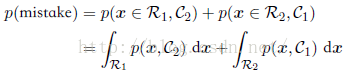
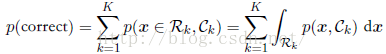
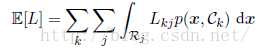
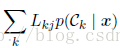
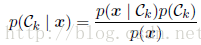
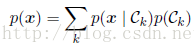
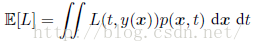
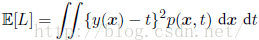
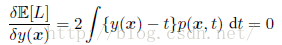
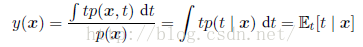
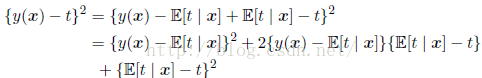
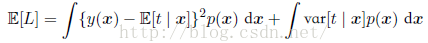
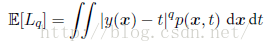
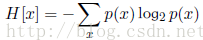
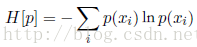
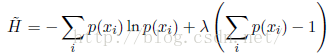
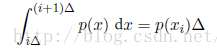
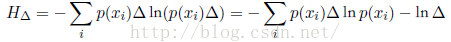
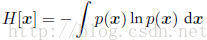
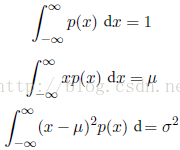
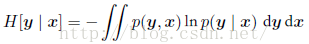
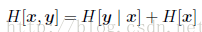
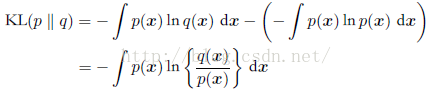
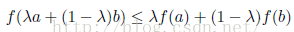
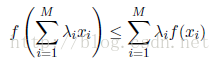
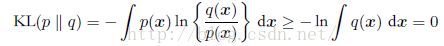
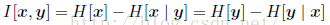













 9万+
9万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








