回溯算法 | 77. 组合 216.组合总和III 17.电话号码的字母组合

77. 组合

题目链接： 77. 组合 - 力扣（LeetCode）
文章讲解：代码随想录
视频讲解：带你学透回溯算法-组合问题（对应力扣题目：77.组合）| 回溯法精讲！

思路

1. 把问题抽象为如下树形结构：[根据下一个数选哪个构造树]
   
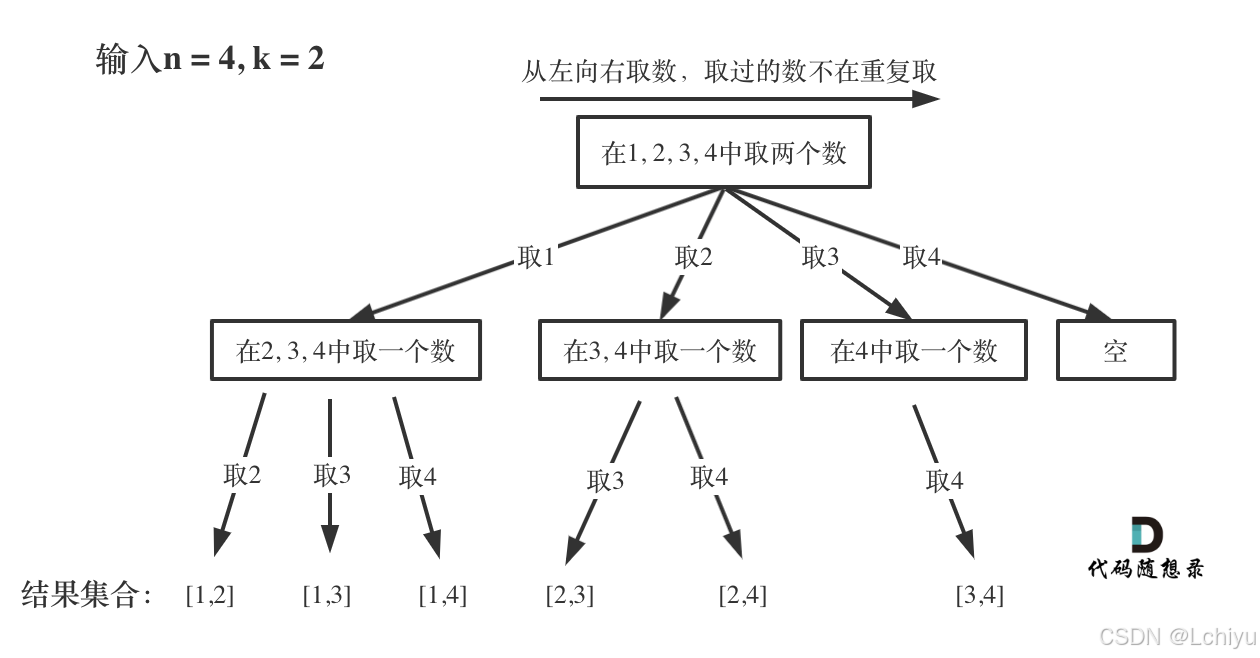
   图中可以发现n相当于树的宽度，k相当于树的深度。图中每次搜索到了叶子节点，就找到了一个结果。代码中的path存的就是根节点到叶子节点的路径
2. 【时间复杂度：分析回溯问题的时间复杂度，有一个通用公式：路径长度×搜索树的叶子数。O(k⋅C(n,k))
   空间复杂度：O(k*n)】
3. 剪枝：当剩余元素小于我们的要求时，不需要继续遍历
4. 除了按上面的方式构造二叉树外，还可以按照每一个数选与不选画出二叉树，二叉树最多n层：
   

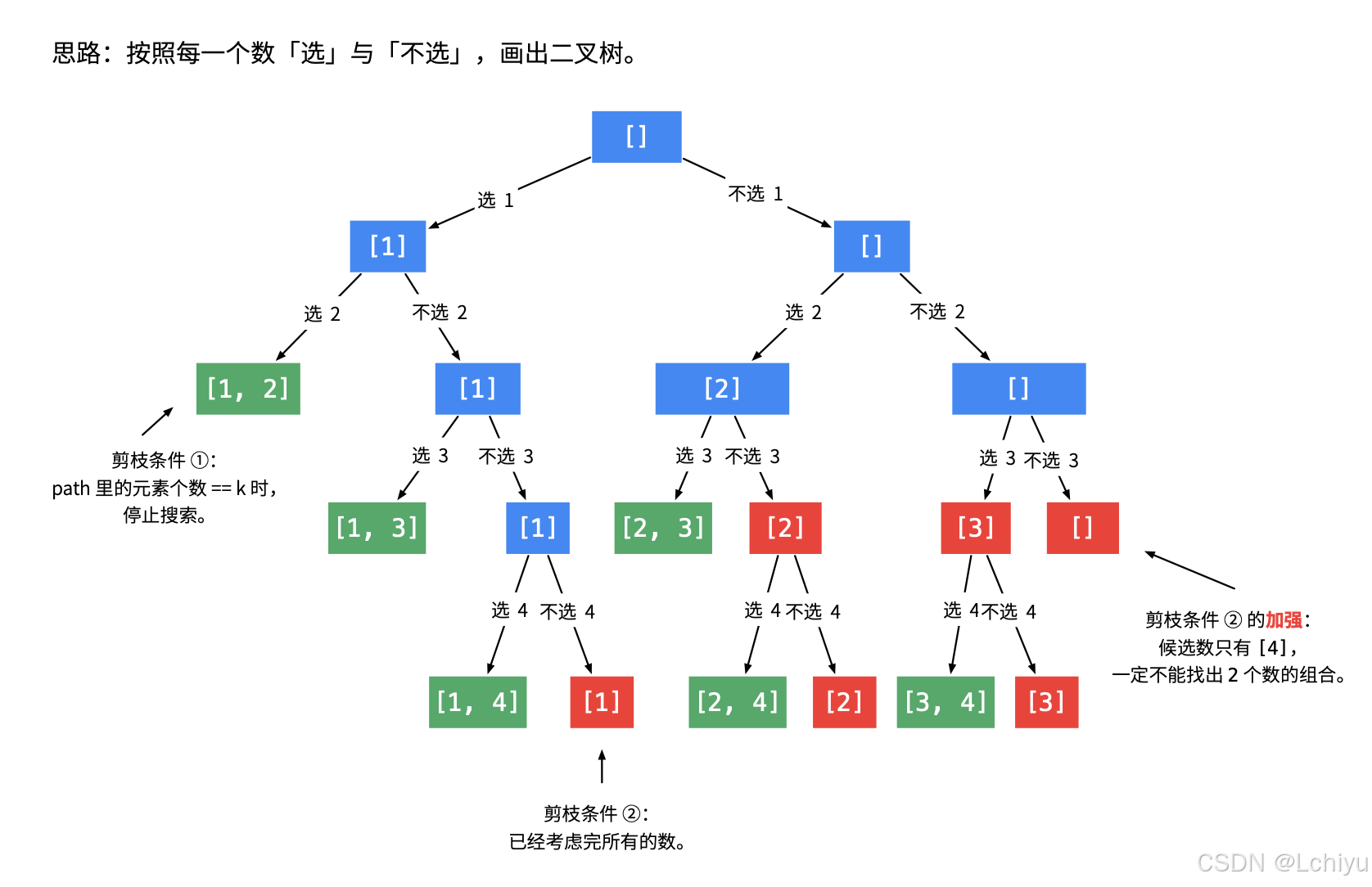
下一个数选哪个

class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        result = []
        path = []
        def dfs(s):
            if len(path) == k:
                result.append(path.copy())
                return 
            if len(s) < k-len(path): # 剪枝
                return
            for i in range(len(s)): # 控制树的横向遍历
                path.append(s[i]) # 处理节点
                dfs(s[i+1:]) # 递归：控制树的纵向遍历
                path.pop() # 回溯，撤销处理的节点

        s = []
        for i in range(n):
            s.append(i+1)
        dfs(s)
        return result

下一个数选哪个的另一种写法

class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        result = []  # 存放结果集
        self.backtracking(n, k, 1, [], result)
        return result
    def backtracking(self, n, k, startIndex, path, result):
        if len(path) == k:
            result.append(path[:])
            return
        for i in range(startIndex, n - (k - len(path)) + 2):  # 优化的地方：搜索起点有上界
            path.append(i)  # 处理节点
            self.backtracking(n, k, i + 1, path, result)
            path.pop()  # 回溯，撤销处理的节点

每一个数选与不选

class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        result = []
        path = []
        def backtracking(i):
            # 终止条件
            if len(path) == k:
                result.append(path[:])
                return
            if i > n: # 可删
                return
            if i > n-(k-len(path))+1: # 剪枝
                return
            
            # 不选
            backtracking(i+1)

            # 选
            path.append(i)
            backtracking(i+1)
            path.pop()
        backtracking(1)
        return result

216.组合总和III

题目链接： 216.组合总和III - 力扣（LeetCode）
文章讲解：代码随想录
视频讲解：和组合问题有啥区别？回溯算法如何剪枝？| LeetCode：216.组合总和III

思路

1. 剪枝：path中元素总和大于n，返回；剩余元素个数小于我们需要的个数，返回

下一个选哪个数

class Solution:
    def combinationSum3(self, k: int, n: int) -> List[List[int]]:
        result = []
        path = []
        s = [1,2,3,4,5,6,7,8,9]
        def backtracking(startIndex,sumPath):
            # 剪枝
            if sumPath > n:
                return

            if len(path) == k:
                if sumPath == n:
                    result.append(path[:])
                return
            
            for i in range(startIndex,10-(k-len(path))): # 剪枝
                path.append(s[i])
                backtracking(i+1,sumPath+s[i])
                path.pop()
        
        backtracking(0,0)
        return result     

下一个数选与不选

class Solution:
    def combinationSum3(self, k: int, n: int) -> List[List[int]]:
        result = []
        path = []
        def backtracking(i,sumPath):
            if len(path) == k:
                if sumPath == n:
                    result.append(path[:])
                return
            if i > 10-(k-len(path)): # 剪枝
                return
            if i > 9: # 可删
                return
            
            # 不选
            backtracking(i+1,sumPath)
            # 选
            path.append(i)
            backtracking(i+1,sumPath+i)
            path.pop()
        
        backtracking(1,0)
        return result

17.电话号码的字母组合

题目链接： 17.电话号码的字母组合- 力扣（LeetCode）
文章讲解：代码随想录
视频讲解：还得用回溯算法！| LeetCode：17.电话号码的字母组合

思路

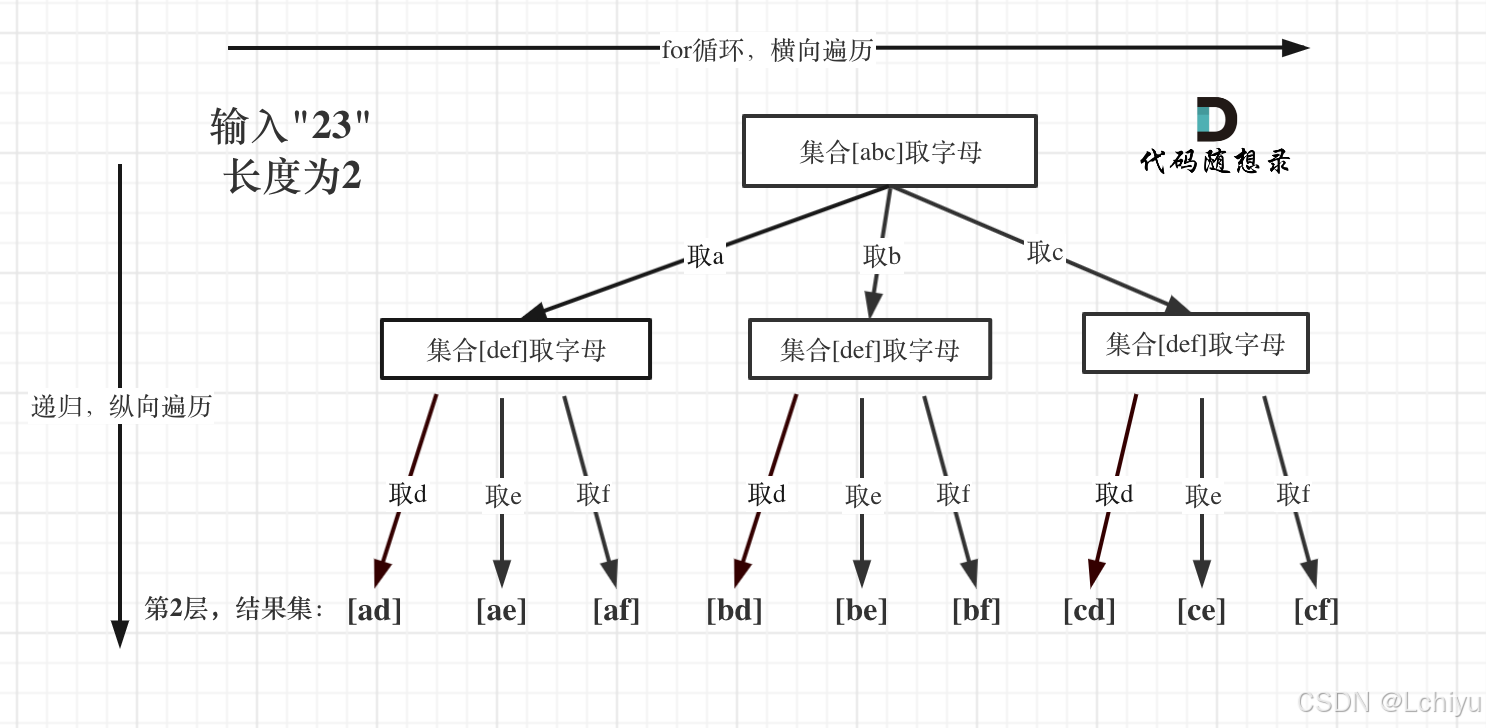
回溯

class Solution:
    def letterCombinations(self, digits: str) -> List[str]:        
        MAPPING = ['','','abc','def','ghi','jkl','mno','pqrs','tuv','wxyz']
        result = []
        n = len(digits)
        if n == 0:
            return []
        
        def backtracking(string,k):
            if len(string) == n:
                result.append(string)
                return
            for s in MAPPING[int(digits[k])]:
                backtracking(string+s,k+1)
        
        backtracking('',0)
        return result