Trie树

Trie树的基本性质：
1、根节点 不包含任何字符，除根节点之外的任何一个节点都只包含一个 字符
2、从根节点到某一节点，将路径上的字符串连接起来，为该节点所对应的字符串。
3、每个节点的所有子节点包含的字符各不相同。

以{“a”, “to”, “tea”, “ted”, “ten”, “i”, “in”, “inn”} 集合构建trieTree树，该树构建完如下所示，

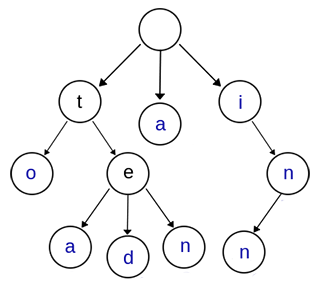
其中在每一个节点中，有一个count变量，来表示从根节点到该节点所代表的的字符串出现的次数。如果count=0，则代表不构成一个字符串。比如第三层最右边的节点中，count=1，此时表示”in”出现了一次；若节点还有子节点，则表示目前为止的字符串还没有结束。在本例中第三层最右边的节点还有子节点，表示”in”后边还有字符，该字符为”n”，字符串为为”inn”。

下边以集合{“the”, “a”, “there”, “answer”, “any”, “by”, “bye”, “their”,”the”}来构建trieTree

#include <iostream>
#include <string>
using namespace std;
const int Alphabet_Size=26; //定义字符个数
typedef struct trieTree
{
    int count; //记录该节点代表的单词个数
    trieTree* children[Alphabet_Size]; //各个子节点
}trieTree;
trieTree* create_trieTree_node()//创建trieTree节点
{
    trieTree* root=new trieTree();
    root->count=0;
    for(int i=0;i<Alphabet_Size;i++)
    {
        root->children[i]=NULL;
    }
    return root;
}
void insert_trieTree(trieTree* root,string key)
{
    trieTree* p=root;
    for(int i=0;i<key.size();i++)
    {
        int index=key[i]-'a';
        if(p->children[index]==NULL)
        {
            p->children[index]=create_trieTree_node();
        }
        p=p->children[index];//改变指针
    }
    p->count+=1;
}
int search_trieTree(trieTree* root,string key)
{
    trieTree* p=root;
    int i=0;
    while( p && i<key.size() )
    {
        int index=key[i]-'a';
        p=p->children[index];
        ++i;
    }
    //如果能找到key的话，那么p节点一定不为空
    if( p!=NULL )
        return p->count;
    else
        return 0;

}
int main()
{
    char keys[][8]={"the", "a", "there", "answer", "any", "by", "bye", "their","the"};
    trieTree* root=create_trieTree_node();
    for(int i=0;i<9;i++) //创建trieTree
    {
        insert_trieTree(root,keys[i]);
    }
    printf("%s --- %d\n", "the", search_trieTree(root, "the") );
    printf("%s --- %d\n", "these", search_trieTree(root, "these") );
    printf("%s --- %d\n", "their", search_trieTree(root, "their") );
    printf("%s --- %d\n", "thaw", search_trieTree(root, "thaw") );
    return 0;
}