Android学习小Demo（4）贝塞尔曲线跟翻页效果

最新推荐文章于 2024-05-17 09:44:15 发布

MaximusKiang

最新推荐文章于 2024-05-17 09:44:15 发布

阅读量987

点赞数

分类专栏： Android_Custom_View 文章标签： android android开发动画移动

Android_Custom_View 专栏收录该内容

8 篇文章 0 订阅

订阅专栏

From:http://blog.csdn.net/linmiansheng/article/details/18568493

第一次看到翻页效果的时候，觉得真是厉害，真是想不出是怎么做的呢（唉，牛人的智商真是只能仰望！）。

直到看了Android 实现书籍翻页效果----原理篇一文，看了何明桂对翻页效果的一张图解，看到贝塞尔曲线，才恍然大悟，只能内心赞叹了。

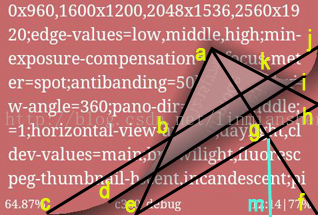
下面先看看图（这张图是直接拿何明桂大牛的，请多多包涵）：

这里是是以右下角为起点来翻页的，但其实只要将右下角的 f 点设成一个变量（它可以是任何一个角）就可以实现四个角的翻页效果了。

这个翻面效果其实是由三部分组成的：当前页、当前页页背和下一页

何大牛的思路是1）先求出页背跟下一页区域，作为path0, 然后利用clippath 的 Region.Op.XOR 来求出当前页。

2）求出下一页的path1，再根据clippath的Region.Op.Difference 来从path0中剪出页背的区域。

而path0，其实就是由jik（贝塞尔曲线，h为控制点），ka（直线），ab（直线），bdc（贝塞尔曲线，以e为控制点），cf（直线），fj（直线）组成的。

而path1，则是由cd（贝塞尔曲线，d为控制点）,di（直线），ij（贝塞尔曲线，以d为控制点）,jf（直线）。

思路既然清楚了，那么当然首先是要来计算点的位置了，何大牛也已经把各个点怎么算的逻辑在上文中给出了，不过我觉得对于其中的b,k 两点，何大牛是想多了。

何大牛是利用两直线相交来算出其交点位置的，何大牛原文如下：

综上，4点相交的直线的交点为：

x=( (x4*y3-y4*x3)/(x4-x3)-(x2*y1-y2*x1)/(x2-x1)) /

((y2-y1)/(x2-x1)- (y4-y3)/(x4-x3) )

= ( (x4*y3-y4*x3) (x2-x1)- (x2*y1-y2*x1) (x4-x3) ) /

( (y2-y1) (x4-x3)- (y4-y3) (x2-x1) )

将之前求得的 a,e,c,j四个点带入上式则可以求出 b. 同理可求k点。

但其实在原先的描述中，cj 这条直线是垂直平分ag的，也就是说其平行于三角形的底并平分其底边上的垂线的，那么根据相似三角形的定理可以知道，b点和k点也应该是其边ae和ah的中点。所以，这两点的坐标可以直接根据ae点和ah点算出来的。

各个点的计算逻辑如下：

[java] view plain copy print ?

private void calculatePoints(){
fx = cornerX;//这是界面的四个顶点之一，可以根据手指落下时来判断是从哪个顶点来翻
fy = cornerY;
gx = (ax + fx) / 2;//g点是af的中点
gy = (ay + fy) / 2;
float gm = fy - gy;
float mf = fx - gx;
float em = gm * gm / mf;//根据相似三角形算出em的长度
ex = gx - em;//算出e点
ey = fy;
float hm = mf * mf / gm;
hx = fx;
hy = gy - hm;//同理，算出h点
cx = ex - (fx - ex)/2;//再同理，三角形ehf跟三角形cjf是相似的，且根据cj是平分ag的，所以在边上的比例是2/3的关系
cy = fy;
jx = fx;
jy = hy - (fy - hy)/2;//同上
bx = (ax + ex) / 2;
by = (ay + ey) / 2;//b点其实就是ae的中点
kx = (ax + hx) / 2;
ky = (ay + hy) / 2;//k点就是ah的中点
//p middle point of the bc;
float px = (bx + cx) / 2; //这里求p点，其实是为了求d点，因为这一段贝塞尔曲线是对称的，
float py = (by + cy) / 2; //<SPAN style="FONT-SIZE: 12px; FONT-FAMILY: Arial, Helvetica, sans-serif">所以求出bc的中点p，跟控制点e连起来，穿过的点d刚好就是在曲线的中点</SPAN>
dx = (px + ex) / 2;
dy = (py + ey) / 2;
px = (kx + jx) / 2; //同上
py = (ky + jy) / 2;
ix = (px + hx) / 2;
iy = (py + hy) / 2;
}

	private void calculatePoints(){					
		fx = cornerX;//这是界面的四个顶点之一，可以根据手指落下时来判断是从哪个顶点来翻
		fy = cornerY;
		
		gx = (ax + fx) / 2;//g点是af的中点
		gy = (ay + fy) / 2;
		
		float gm = fy - gy;
		float mf = fx - gx;
		float em = gm * gm / mf;//根据相似三角形算出em的长度
		
		ex = gx - em;//算出e点
		ey = fy;
			
		float hm = mf * mf / gm;
		
		hx = fx;
		hy = gy - hm;//同理，算出h点
		
		
		cx = ex - (fx - ex)/2;//再同理，三角形ehf跟三角形cjf是相似的，且根据cj是平分ag的，所以在边上的比例是2/3的关系
		cy = fy;
		
		jx = fx;
		jy = hy - (fy - hy)/2;//同上
		
		bx = (ax + ex) / 2;
		by = (ay + ey) / 2;//b点其实就是ae的中点
		
		kx = (ax + hx) / 2;
		ky = (ay + hy) / 2;//k点就是ah的中点
		
		//p middle point of the bc;
		float px = (bx + cx) / 2; //这里求p点，其实是为了求d点，因为这一段贝塞尔曲线是对称的，
		float py = (by + cy) / 2; //<span style="font-family:Arial, Helvetica, sans-serif;font-size:12px;">所以求出bc的中点p，跟控制点e连起来，穿过的点d刚好就是在曲线的中点</span>

		
		dx = (px + ex) / 2;
		dy = (py + ey) / 2;
			
		
		px = (kx + jx) / 2; //同上
		py = (ky + jy) / 2;
		
		ix = (px + hx) / 2;
		iy = (py + hy) / 2;		
	}

既然点出来了，那么就利用path的quadTo和lineTo，还有close来画出封闭的贝塞尔曲线，就是要画出来的区域了。

[java] view plain copy print ?

canvas.save();
path.reset();
path.moveTo(jx, jy);
path.quadTo(hx, hy, kx, ky);
path.lineTo(ax, ay);
path.lineTo(bx, by);
path.quadTo(ex, ey, cx, cy);
path.lineTo(fx, fy);
path.close();
paint.setColor(Color.GREEN); //画绿色
canvas.drawPath(path, paint);
canvas.restore();

		canvas.save();			
		path.reset();
		path.moveTo(jx, jy);
		path.quadTo(hx, hy, kx, ky);
		path.lineTo(ax, ay);
		path.lineTo(bx, by);
		path.quadTo(ex, ey, cx, cy);
		path.lineTo(fx, fy);
		path.close();						
		paint.setColor(Color.GREEN);		//画绿色
		canvas.drawPath(path, paint);
		canvas.restore();

画出 path0，从j点到f点，然后利用close把曲线给封闭起来。

[java] view plain copy print ?

canvas.save();
canvas.clipRect(canvas.getClipBounds());//clip出整个界面
canvas.clipPath(path,Op.XOR); //clip出path0的区域，然后根据XOR，取出path0没有圈住的区域
canvas.drawColor(Color.RED); //画红色
canvas.restore();

		canvas.save();
		canvas.clipRect(canvas.getClipBounds());//clip出整个界面
		canvas.clipPath(path,Op.XOR);		//clip出path0的区域，然后根据XOR，取出path0没有圈住的区域
		canvas.drawColor(Color.RED);		//画红色
		canvas.restore();

利用异或的操作（异或其实就是我们俩都占了的地方，就不能给你了），截出当前页。

最后再利用difference操作，截取出页背部分，

[java] view plain copy print ?

canvas.clipPath(path);
pathNext.reset();
pathNext.moveTo(cx, cy);
pathNext.quadTo(dx, dy, dx, dy);
pathNext.lineTo(ix, iy);
pathNext.quadTo(jx, jy, jx, jy);
pathNext.lineTo(fx, fy);
pathNext.close();
canvas.clipPath(pathNext, Op.DIFFERENCE);//difference最取出两段path中不同的地方
canvas.drawColor(Color.YELLOW);
canvas.restore();

                canvas.clipPath(path);
		pathNext.reset();
		pathNext.moveTo(cx, cy);
		pathNext.quadTo(dx, dy, dx, dy);
		pathNext.lineTo(ix, iy);
		pathNext.quadTo(jx, jy, jx, jy);
		pathNext.lineTo(fx, fy);
		pathNext.close();
		canvas.clipPath(pathNext, Op.DIFFERENCE);//difference最取出两段path中不同的地方
		canvas.drawColor(Color.YELLOW);
		canvas.restore();

这样，就把这几个区域都给取出来了，当我们Touch的时候，根据手指移动的坐标，进行重复的计算，从而拉出翻页的效果，当我们手指抬起的时候，就利用一个动画效果，把页面直接给翻过去。

下面是一个小Demo，我们来看看效果图：